ML Aggarwal Circles Exe-15.1 Class 10 ICSE Maths Solutions. We Provide Step by Step Answer of Exe-15.1 Questions for Circles as council prescribe guideline for upcoming board exam. Visit official Website CISCE  for detail information about ICSE Board Class-10.

ML Aggarwal Circles Exe-15.1 Class 10 ICSE Maths Solutions

Board	ICSE
Subject	Maths
Class	10th
Chapter-15	Circles
Writer / Book	Understanding
Topics	Solutions of Exe-15.1
Academic Session	2024-2025

Circles Exe-15.1

ML Aggarwal Class 10 ICSE Maths Solutions

(Page 320)

Question 1. Using the given information, find the value of x in each of the following figures :

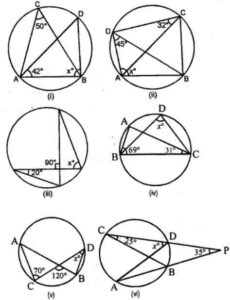
Answer :

(i) ∠ADB and ∠ACB are in the same segment.

∠ADB = ∠ACB = 50°
Now in ∆ADB,
∠DAB + X + ∠ADB = 180°

= 42° + x + 50° = 180°

= 92° + x = 180°

x = 180° – 92°

x = 88°

(ii) In the given figure we have

= 32° + 45° + x = 180°

= 77° + x = 180°

x = 103°

(iii) From the given number we have

∠BAD = ∠BCD

∠BAD = 20°

∠BCD = 20°

∠CEA = 90°

∠CED = 90°

Now in triangle CED,

∠CED + ∠BCD + ∠CDE = 180°

⇒ 90° + 20° + x = 180°

⇒ 110° + x = 180°

⇒ x = 180° – 110°

⇒ x = 70°

(iv) In ∆ABC

∠ABC + ∠ABC + ∠BAC = 180°

⇒ 69° + 31° + ∠BAC = 180°

⇒ ∠BAC = 180° – 100°

⇒ ∠BAC = 80°

Since, ∠BAC and ∠BAD are in the same

Segment.

∠BAD = x° = 80°

(v) Given ∠CPB = 120°, ∠ACP = 70°

To find, x° i,e., ∠PBD

Reflex ∠CPB = ∠BPO + ∠CPA

⇒ 120° = ∠BPD + ∠BPD

(BPD = CPA are vertically opposite ∠s)

⇒ 2∠BPD = 120°

⇒ ∠PBD = 120°/2 = 60°

Also ∠ACP and PBD are in the same segment

∠PBD + ∠ACP = 70°

Now, In ∆PBD

∠PBD + ∠PDB + ∠BPD = 180°

(sum of all ∠s in a triangle)

70° + x° + 60° = 180°

⇒ x = 180° – 130°

⇒ x = 50°

(vi) ∠DAB = ∠BCD

(Angles in the same segment of the circle)

∠DAB = 25° (∠BCD = 25° given)

In ∆DAP,

Ex. ∠CDA = ∠DAP + ∠DPA

⇒ x° = ∠DAB + ∠DPA

⇒ x° = 25° + 35°

⇒ x° = 60°

---

Circles Exe-15.1

ML Aggarwal Class 10 ICSE Maths Solutions

(Page 321)

Question 2. If O is the centre of the circle, find the value of x in each of the following figures (using the given information):

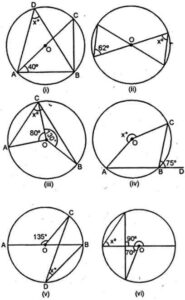
Answer :

(i) ∠ACB = ∠ADB

(Angles in the same segment of a circle)
But ∠ADB = x°

∠ABC = x°

Now in ∆ABC

∠CAB + ∠ABC + ∠ACB = 180°

⇒ 40° + 90° + x° = 180°

(AC is the diameter)

⇒ 130° ⁺ x° = 180°

⇒ x° = 180° – 130° = 50°

(ii) ∠ACD = ∠ABD

(angles in the same segment)

∠ACD = x°

Now in triangle OAC,

OA = OC

(radii of the same circle)

∠ACO = ∠AOC

(opposite angles of equal sides)

Therefore, x° = 62°

(iii) ∠AOB + ∠AOC + ∠BOC = 360°

(sum of angles at a point)

∠AOB + 80° + 130° = 360°

⇒ ∠AOB + 210° = 360°

⇒ ∠AOB = 360° – 210° = 150°

Now arc AB subtends ∠AOB at the center ∠ACB at the remaining part of the circle

∠AOB = 2 ∠ACB

⇒ ∠ACB = ½ ∠AOB = ½ × 150° = 75°

(iv) ∠ACB + ∠CBD = 180°

⇒ ∠ABC + 75° = 180°

⇒ ∠ABC = 180° – 75° = 105°

Now arc AC Subtends reflex ∠AOC at the center and ∠ ABC at the remaining part of the circle.

Reflex ∠AOC = 2 ∠ABC

= 2 × 105° 

= 210°

(v) ∠AOC + ∠COB = 180°

⇒ 135° + ∠COB = 180°

⇒ ∠COB = 180° – 135° = 45°

Now arc BC Subtends reflex ∠COB at the center and ∠ CDB at the remaining part of the circle.

∠COB = 2 ∠CDB

⇒∠CDB = ½ ∠COB

= ½ × 45^o = 45^o/2 = 22 1/2^o

(vi) Arc AB subtends ∠AOD at the center and ∠ACD at the remaining part of the Circle

∠AOD = 2 ∠ACB

⇒ ∠ACB = ½ ∠AOD = ½ × 70^o = 35^o

∵ ∠CMO = 90^o

∴ ∠AMC = 90^o

(∴∠AMC + ∠CMO = 180^o)

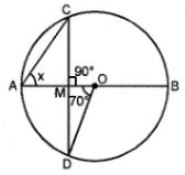
∠ACM + ∠AMC + ∠CAM = 180^o

⇒ 35^o + 90^o + x^o = 180^o

⇒ 125^o + x^o = 180^o

⇒ x^o = 180 – 125^o = 55^o

Question 3.

(a) In the figure (i) given below, AD || BC. If ∠ACB = 35°. Find the measurement of ∠DBC.
(b) In the figure (ii) given below, it is given that O is the centre of the circle and ∠AOC = 130°. Find ∠ABC

Answer :

(a) Construction: Join AB

∠A = ∠C = 35° [∵ Alt angles]

⇒ ∠ABC = 35^o

(b) ∠AOC + reflex ∠AOC = 360^o

⇒ 130^o + Reflex ∠AOC = 360^o

⇒ Reflex ∠AOC = 360^o – 130^o = 230^o

Now, arc BC Subtends reflex ∠AOC at the center and ∠ABC at the remaining part of the circle.

Reflex ∠AOC = 2 ∠ABC

⇒ ∠ABC =1/2 reflex ∠AOC

= ½ × 230^o = 115^o

Question 4

(a) In the figure (i) given below, calculate the values of x and y.
(b) In the figure (ii) given below, O is the centre of the circle. Calculate the values of x and y.

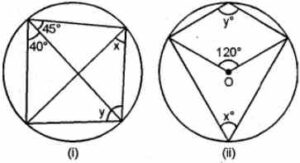
Answer :

(a) ABCD is a cyclic quadrilateral

∠B + ∠D = 180°

⇒ y + 40^° + 45^o = 180^o

(y + 85^o = 180^o)

⇒ y = 180^o – 85^o = 95^o

(∠ACB = ∠ADB)

⇒ x^o = 40

(b) Arc ADC Subtends ∠AOC at the center and ∠ ABC at the remaining part of the circle

∠AOC = 2 ∠ABC

⇒ x^o = 60^o

Again, ABCD is a Cyclic quadrilateral

∠B + ∠D = 180^o

(60^o + y^o = 180^o)

⇒ y = 180^o – 60^o = 120^o

---

Circles Exe-15.1

ML Aggarwal Class 10 ICSE Maths Solutions

(Page 322)

Question 5.

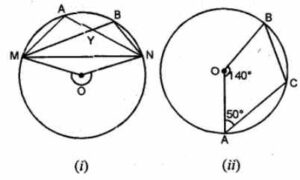
(a) In the figure (i) given below, M, A, B, N are points on a circle having centre O. AN and MB cut at Y. If ∠NYB = 50° and ∠YNB = 20°, find ∠MAN and the reflex angle MON.

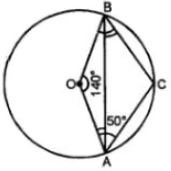
(b) In the figure (ii) given below, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°, find

(i) ∠ACB
(ii) ∠OBC
(iii) ∠OAB
(iv) ∠CBA

Answer :

(a) ∠NYB = 50°, ∠YNB = 20°.

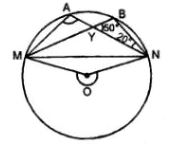
∠NYB + ∠YNB + ∠YBN = 180o

⇒ 50^o + 20^o + ∠YBN = 180^o

⇒ ∠YBN + 70^o = 180^o

⇒ ∠YBN = 180^o – 70^o = 110^o

But ∠MAN = ∠YBN

(Angles in the same segment)

⇒ ∠MAN = 110^o

Major arc MN subtend reflex ∠MON at the

Centre and ∠MAN at the remaining part of the choice.

Reflex ∠MAN at the remaining part of the circle

Reflex ∠MON = 2 ∠MAN = 2×110^o =220^o

(b)

(i) ∠AOB + reflex ∠AOB = 360^o

(Angles at the point)

⇒ 140^o + reflex ∠AOB = 360^o

⇒ Reflex ∠AOB = 360^o – 140^o = 220^o

Now major arc AB subtends ∠AOB+ ∠OBC = 360^o

⇒ 50^o + 110^o + 140^o + ∠OBC =360°

⇒ 300^o + ∠OBC = 360°

⇒ ∠300^o + ∠OBC = 360°

⇒ ∠OBC = 360^o – 300^o

⇒ ∠OBC = 60^o

(ii) In Quadrilateral, OACB

∠OAC + ∠ACB + ∠AOB + ∠OBC = 360^o

⇒ 50^o + 110^o + 140^o + ∠OBC = 360^o

⇒ 300^o + ∠OBC = 360^o

⇒ ∠OBC = 360^o – 300^o

⇒ ∠OBC =60^o

(iii) In ∆OAB,

OA = OB

(Radii of the same circle)

⇒ ∠OAB + ∠OBA = 180^o

⇒ 2∠OAB = 180^o – 140^o = 40^o

⇒ ∠OAB = 40^o/2 = 20°

But, ∠OBC = 60^o

∠CBA = ∠OBC – ∠OBA = 60^o – 20^o = 40^o

Question 6.

 (a) In the figure (i) given below, O is the centre of the circle and ∠PBA = 42°. Calculate the value of ∠PQB
(b) In the figure (ii) given below, AB is a diameter of the circle whose centre is O. Given that ∠ECD = ∠EDC = 32°, calculate
(i) ∠CEF
(ii) ∠COF.

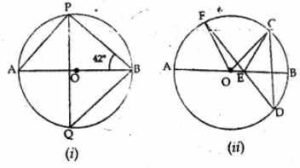
Answer :

(a) In ∆APB,

∠APB = 90° (Angle in a semi-circle)

But ∠A + ∠APB + ∠ABP = 180° (Angles of a triangle)

⇒ ∠A + 90° + 42°= 180°

⇒ ∠A + 132° = 180°

⇒ ∠A = 180° – 132° = 48°

But ∠A = ∠PQB

(Angles in the same segment of a circle)

⇒ ∠PQB = 48^o

(b) 

(i) in ∆EDC,

(Exterior angle of a triangle is equal to the sum of its interior opposite angels)

(ii) arc CF subtends ∠COF at the center and

∠CDF at the remaining part of the circle

∠COF = 2∠CDF = 2∠CDE

= 2×32^o = 2 ∠CDE

= 2×32^o 

= 64

Question 7.

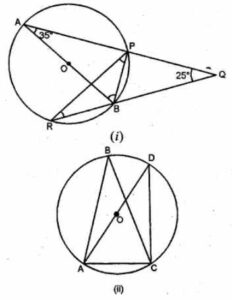
(a) In the figure (i) given below, AB is a diameter of the circle APBR. APQ and RBQ are straight lines, ∠A = 35°, ∠Q = 25°. Find (i) ∠PRB (ii) ∠PBR (iii) ∠BPR.
(b) In the figure (ii) given below, it is given that ∠ABC = 40° and AD is a diameter of the circle. Calculate ∠DAC.

Answer :

(a) (i) ∠PRB = ∠BAP

(Angles in the same segment of the circle)
∴ ∠PRB = 35° (∵ ∠BAP = 35° given)

(ii) In ∆PRQ,

Ext. ∠APR = ∠PRQ + ∠PQR

= ∠PRB + ∠Q

= 35°+25° = 60°

But ∠APB = 90° (Angle in a semi circle)

∴ ∠BPR = ∠APB – ∠APR

= 90° -60° = 30°

(iii) ∠APR = ∠ABR

⇒ ∠ABR = 60°

In △PBQ,

Ext. ∠PBR = ∠Q + ∠BPQ

= 25° + 90° = 115°

(b) ∠B = ∠D (Angles in the same segment)

∴ ∠C = 40°

∠ACD = 90° (Angle in the semi circle)

Now in △ADC,

∠ACD + ∠D + ∠DAC = 180° (Angles in a triangle)

⇒ 90° + 40° + ∠DAC = 180°

⇒ 130° + ∠DAC = 180°

⇒ ∠DAC = 180° – 130° = 50°

---

Circles Exe-15.1

ML Aggarwal Class 10 ICSE Maths Solutions

(Page 323)

Question 8

(a) In the figure given below, P and Q are centers of two circles intersecting at B and C. ACD is a straight. line. Calculate the numerical value of x.

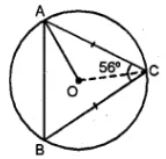
(b) In the figure given below, O is the circumcenter of triangle ABC in which AC = BC. Given that ∠ACB = 56°, calculate

(i)∠CAB
(ii)∠OAC

Answer :

Given that:

(a) Arc AB subtends ∠APB at the centre and ∠ACB at the remaining part of the circle

∠ACB = ½ ∠APB = ½ × 130^o = 65^o

But ∠ACB + ∠BCD = 180^o (Linear Pair)

⇒ 65^o + ∠BCD = 180^o

⇒ ∠BCD = 180^o – 65^o = 115^o

Major arc BD subtends reflex ∠BQD at the

Centre and ∠BCD at the remaining part of the circle reflex ∠BQD = 2∠BCD

= 2×115^o = 230°

But reflex ∠BQD + x = 360^o (Angles at a point)

⇒ 230^o + x = 360^o

⇒ x = 360^o – 230^o = 130^o

(b) Join OC

In ∆ABC,

AC = BC

∠A = ∠B

But ∠A + ∠B + ∠C = 180^o

⇒ ∠A + ∠A + 56° = 180°

⇒ 2∠A = 180^o – 56° = 124^o

⇒ ∠A = 124/2 = 62^o or ∠CAB = 62°

OC is the radius of the circle. OC bisects ∠ACB.

∠OCA = ½∠ACB = ½×56^o = 28^o

Now in ∆OAC

OA = OC (radii of the same Circle)

∠OAC = ∠OCA = 28^o

Question 9.

(a) In the figure (i) given below, chord ED is parallel to the diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.

(b) In the figure (ii) given below, C is a point on the minor arc AB of the circle with centre O. Given ∠ACB = p°, ∠AOB = q°, express q in terms of p. Calculate p if OACB is a parallelogram.

Answer :

(a) ∠CBE = ∠CAE

(Angle in the same segment of a circle)
⇒ ∠CAE = 65°
∠AEC = 90° (Angle in a semi circle)
Now in ∆AEC
∠AEC + ∠CAE + ∠ACE = 180° (Angle of a triangle)
⇒ 90°+ 65° +∠ACE = 180°
so ⇒ 155° + ∠ACE = 180°
hence ⇒ ∠ACE = 180° – 155° – 25°
∵AC || ED (given)
∴∠ACE = ∠DEC (alternate angles)
∴∠DEC = 25°

Question 10.

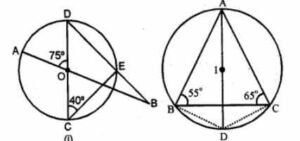
(a) In the figure (i) given below, straight lines AB and CD pass through the centre O of a circle. If ∠OCE = 40° and ∠AOD = 75°, find the number of degrees in :

(i) ∠CDE
(ii) ∠OBE.

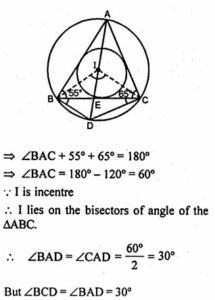
(b) In the figure (ii) given below, I is the incentre of ∆ABC. AI produced meets the circumcircle of ∆ABC at D. Given that ∠ABC = 55° and ∠ACB = 65°, calculate

(i) ∠BCD
(ii) ∠CBD
(iii) ∠DCI
(iv) ∠BIC.

Answer :

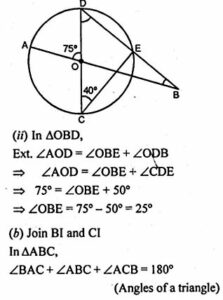
(a) (i) ∠CED = 90° (Angle in semi-circle)

In ∆CED
∠CED + ∠CDE + ∠DCE = 180°
so ⇒ 90° +∠CDE + 40° = 180°
therefore ⇒ 130° + ∠CDE = 180°
hence  ⇒ ∠CDE = 180° – 130° = 50°

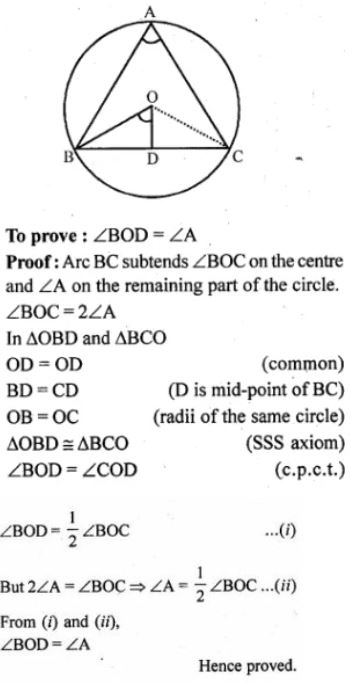
Question 11. O is the circumcenter of the triangle ABC and D is mid-point of the base BC. Prove that ∠BOD = ∠A.

Answer :

In the given figure, O is the centre of circumcenter of ∆ABC.
D is mid-point of BC. BO, CO and OD are joined.

---

Circles Exe-15.1

ML Aggarwal Class 10 ICSE Maths Solutions

(Page 324)

Question 12. In the adjoining figure, AB and CD are equal chords. AD and BC intersect at E. Prove that AE = CE and BE = DE.

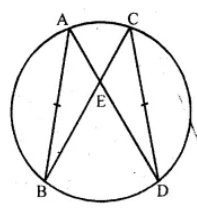
Answer :

In the given figure, AB and CD are two equal chords
AD and BC intersect each other at E.
To prove : AE = CE and BE = DE
Proof:
In ∆AEB and ∆CED
AB = CD (given)
∠A = ∠C (angles in the same segment)
∠B = ∠D (angles in the same segment)
∴ ∆AEB ≅ ∆CED (ASA axiom)
∴ AE = CE and BE = DE (c.p.c.t.)

Question 13.

(a) In the figure (i) given below, AB is a diameter of a circle with centre O. AC and BD are perpendiculars on a line PQ. BD meets the circle at E. Prove that AC = ED.

(b) In the figure (ii) given below, O is the centre of a circle. Chord CD is parallel to the diameter AB. If ∠ABC = 25°, calculate ∠CED.

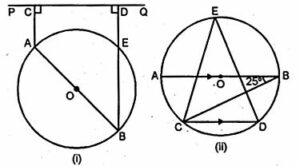
Answer :

(a) Given: AB is the diameter of a circle with centre O.

AC and BD are perpendiculars on a line PQ,
such that BD meets the circle at E.

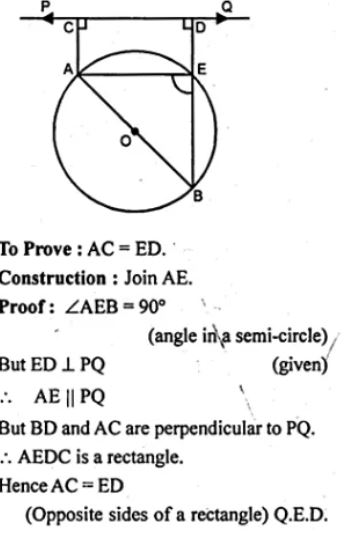
Question 14. In the adjoining figure, O is the centre of the given circle and OABC is a parallelogram. BC is produced to meet the circle at D.

Prove that ∠ABC = 2 ∠OAD.

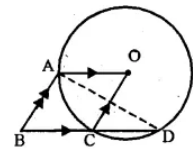
Answer :

Given: In the figure,

OABC is a || gm and O is the centre of the circle.
BC is produced to meet the circle at D.
To Prove : ∠ABC = 2∠OAD.
Construction: Join AD.

Question 15.

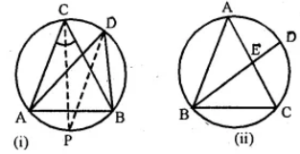
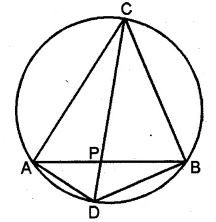
(a) In the figure (i) given below, P is the point of intersection of the chords BC and AQ such that AB = AP. Prove that CP = CQ.

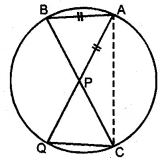
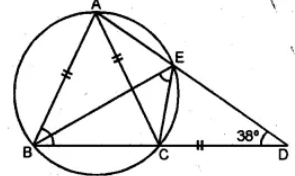
(b) In the figure (i) given below, AB = AC = CD, ∠ADC = 38°. Calculate :
(i) ∠ABC (ii) ∠BEC.

Answer :

(a) Given:

Two chords AQ and BC intersect each other at P
inside the circle. AB and CQ are joined and AB = AP.
To Prove : CP = CQ
Construction : Join AC.
Proof: In ∆ABP and ∆CQP
∴ ∠B = ∠Q

---

Circles Exe-15.1

ML Aggarwal Class 10 ICSE Maths Solutions

(Page 325)

Question 16.

(a) In the figure (i) given below, CP bisects ∠ACB. Prove that DP bisects ∠ADB.
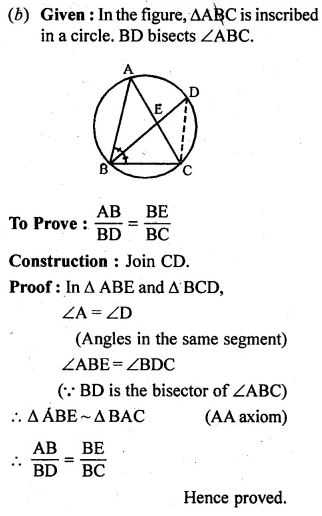
(b) In the figure (ii) given below, BD bisects ∠ABC. Prove that AB/BD=BE/BC

Answer :

(a)Given: In the figure, CP is the bisector of

∠ACB meeting the circle at P.
PD is joined

Question 17.

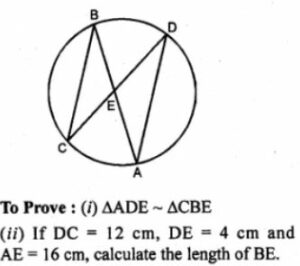
(a) In the figure (ii) given below, chords AB and CD of a circle intersect at E.

(i) Prove that triangles ADE and CBE are similar.
(ii) Given DC =12 cm, DE = 4 cm and AE = 16 cm, calculate the length of BE.

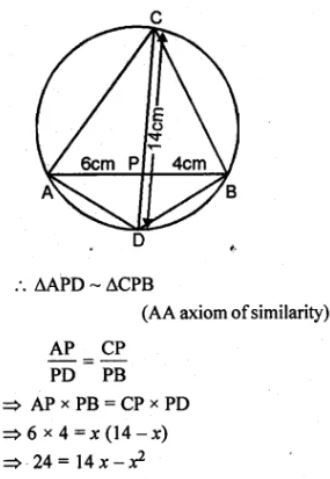
(b) In the figure (ii) given below, AB and CD are two intersecting chords of a circle. Name two triangles which are similar. Hence, calculate CP given that AP = 6cm, PB = 4 cm, and CD = 14 cm (PC > PD).

Answer :

(a) Given: Two chords AB and CD intersect each other

at E inside the circle.

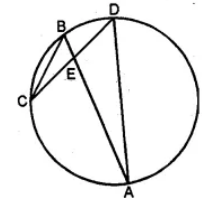
Question 18. In the adjoining figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find DE. (2008)

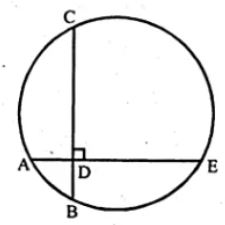
Answer :

In the figure, AE and BC intersect each other at D.
AB is joined.

Question 19.

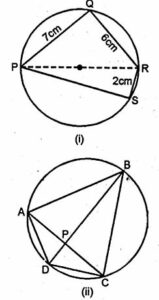
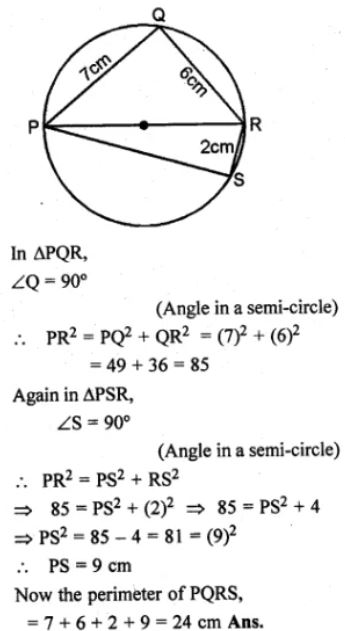
 (a) In the figure (i) given below, PR is a diameter of the circle, PQ = 7 cm, QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.
(b) In the figure (ii) given below, the diagonals of a cyclic quadrilateral ABCD intersect in P and the area of the triangle APB is 24 cm². If AB = 8 cm and CD = 5 cm, calculate the area of ∆DPC.

Answer :

(a) PR is the diameter of the circle
PQ = 7 cm, QR = 6 cm, RS = 2 cm.

---

Circles Exe-15.1

ML Aggarwal Class 10 ICSE Maths Solutions

(Page 326)

Question 20.

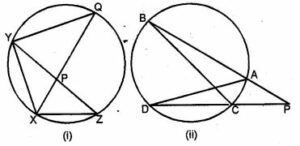
 (a) In the figure (i) given below, QPX is the bisector of ∠YXZ of the triangle XYZ. Prove that XY : XQ = XP : XZ,
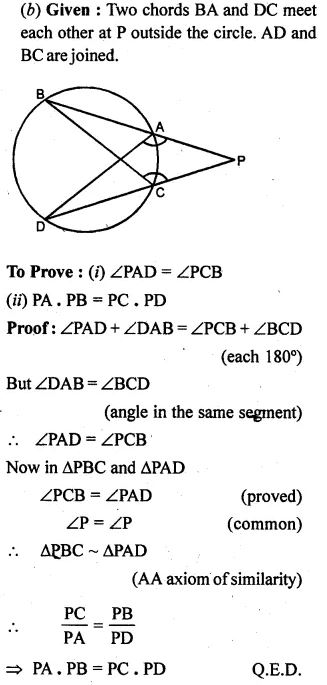
(b) In the figure (ii) given below, chords BA and DC of a circle meet at P. Prove that:

(i) ∠PAD = ∠PCB
(ii) PA. PB = PC . PD.

Answer :

(a) Given: ∆XYZ is inscribed in a circle.

Bisector of ∠YXZ meets the circle at Q.
QY is joined.
To Prove : XY : XQ = XP : XZ

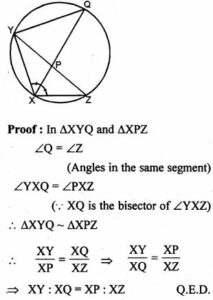
—  : End of ML Aggarwal Circles Exe-15.1 Class 10 ICSE Maths Solutions : –

Return to:   ML Aggarwal Solutions for ICSE Class-10

Thanks

Please Share with Your Friends