Circular Motion Obj-1 HC Verma Solutions Vol-1 Chapter-7 Concept of Physics for Class-11. Step by Step Solutions of Objective -1 (MCQ-1) Questions of Chapter-7 Circular Motion (Concept of Physics) .Visit official Website CISCE for detail information about ISC Board Class-11 Physics.
Circular Motion Obj-1 (MCQ-1) HC Verma Solutions Ch-7 Vol-1 Concept of Physics for Class-11
| Board | ISC and other board |
| Publications | Bharti Bhawan Publishers |
| Chapter-7 | Circular Motion |
| Class | 11 |
| Vol | 1st |
| writer | HC Verma |
| Book Name | Concept of Physics |
| Topics | Solution of Objective-1 (MCQ-1) Questions |
| Page-Number | 112, 113 |
-: Select Topics :-
Objective-I (Currently Open)
Objective-II (update soon)
Exercise (update soon)
Circular Motion Obj-1 (MCQ-1) HC Verma
HC Verma Solutions of Ch-7 Vol-1 Concept of Physics for Class-11
(Page-112)
Question-1 :-
When a particle moves in a circle with a uniform speed
(a) its velocity and acceleration are both constant
(b) its velocity is constant but the acceleration changes
(c) its acceleration is constant but the velocity changes
(d) its velocity and acceleration both change.
Answer-1 :-
The option (d) its velocity and acceleration both change. is correct
Explanation:
In a circular motion, the direction of particle changes. Therefore, velocity, being a vector quantity, also changes.
As the velocity changes, acceleration also changes.
Question-2 :-
Tow cars having masses m1 and m2 moves in circles of radii r1 and r2 respectively. If they complete the circle in equal time, the ratio of their angular speed ω1/ω2 is
(a) m1/m2
(b) r1/r2
(c) m1r1/m2/r2
(d) 1.
Answer-2 :-
The option (d) 1. is correct
Explanation:
1. Time period (T) is same for both the cars.
We know that :
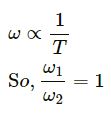
Question-3 :-
A car moves at a constant speed on a road as shown in figure. The normal force by the road on the car NA and NB when it is at the points A and B respectively.
Information to decide the relation of NA and NB.

(a) NA = NB
(b) NA > NB
(c) NA < NB
(d) insufficient
Answer-3 :-
The option (c) NA < NB is correct
Explanation:
From the figure in the question, it is clear that r B > r A.
Here, normal reaction is inversely proportional to the centrifugal force acting on the car, while taking turn on the curve track. Also, centrifugal force is inversely proportional to the radius of the circular track.
Therefore, we have:
NA < NB
Question-4 :-
A particle of mass m is observed from an inertial frame of reference and is found to move in a circle of radius r with a uniform speed v. The centrifugal force on it is
(a) mv²/r towards the centre
(b) mv²/r away from the centre
(c) mv²/r along the tangent through the particle
(d) zero
Answer-4 :-
The option (d) zero is correct
Explanation:
The centrifugal force is a pseudo force and can only be observed from the frame of reference, which is non-inertial w.r.t. the particle.
Question-5 :-
A particle of mass m rotates with a uniform angular speed ω. It is viewed from a frame rotating about the Z-axis with a uniform angular speed ω0. The centrifugal force on the particle is
(a) mω2a
(b) ![]()
(c) 
(d) mω ω0 a.
Answer-5 :-
The option (b) ![]() is correct
is correct
Explanation:
The centrifugal force on the particle depends on the angular speed (ω0) of the frame and not on the angular speed (ω) of the particle. Thus, the value of centrifugal force on the particle is ![]()
Question-6 :-
A particle is kept fixed on a turntable rotating uniformly. As seen from the ground the particle goes in a circle, its speed is 20 cm/s and acceleration is 20 cm/s2. The particle is now shifted to a new position to make the radius half of the original value. The new value of the speed and acceleration will be
(a) 10 cm/s, 10 cm/s2
(b) 10 cm/s, 80 cm/s2
(c) 40 cm/s, 10 cm/s2
(d) 40 cm/s, 40 cm/s2
Answer-6 :-
The option (a) 10 cm/s, 10 cm/s2 is correct
Explanation:
It is given that the turntable is rotating with uniform angular velocity. Let the velocity be ω .
We have:
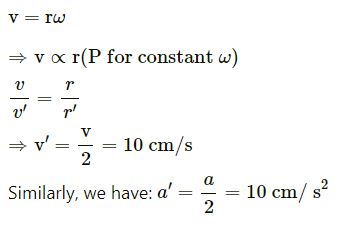
Question-7 :-
Water in a bucket is whirled in a vertical circle with string attached to it. The water does no fall down even when the bucket is inverted at the top of its path. We conclude that in this position
(a) mg =mv²/r
(b) mg is greater than mv²/r
(c) mg is not greater than mv²/r
(d) mg is not less than mv²/r
Answer-7 :-
The option (c) mg is not greater than mv²/r is correct
Explanation:
At the top of the path, the direction of mg is vertically downward and for centrifugal force (mv²/r) , the direction is vertically upward. If the vertically downward force is not greater, water will not fall.
HC Verma Solutions of Ch-7 Vol-1 Concept of Physics for Class-11
Circular Motion Obj-1 (MCQ-1)
(Page-113)
Question-8 :-
A stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
(a) towards the centre
(b) away from the centre
(c) along a tangent
(d) will stop.
Answer-8 :-
The option (c) along a tangent is correct
Explanation:
The stone will move in a circle and the direction of velocity at any instant is always along the tangent at that point. Therefore, the stone will move along the tangent to the circle at a point where the string breaks.
Question-9 :-
A coin placed on a rotating turntable just slips. If it is placed at a distance of 4 cm from the centre. If the angular velocity of the turntable is doubled, it will just slip at a distance of
(a) 1 cm
(b) 2 cm
(c) 4 cm
(d) 8 cm
Answer-9 :-
The option (a) 1 cm is correct
Explanation:
Let the force of friction between the coin and the rotating turntable be F.
For the coin to just slip ,
we have : F = m ω²r
Here, m ω² r is the centrifugal force acting on the coin.
For constant F and m, we have : r∝1/ω²
Therefore,
r′/r=(ω/ω′)²
⇒ r’ = 1 cm
Question-10 :-
A motorcycle is going on an over bridge of radius R. The driver maintains a constant speed. As the motorcycle is ascending on the over bridge, the normal force on it
(a) increases
(b) decreases
(c) remains the same
(d) fluctuates.
Answer-10 :-
The option (a) increases is correct
Explanation:

The normal force on the motorcycle , N = mgcosθ−mv²/R
As the motorcycle is ascending on the over bridge, θ decreases (from π/2 to 0).
So, normal force increases with decrease in θ.
Question-11:-
Three identical cars A, B and C are moving at the same speed on three bridges. The car A goes on a place bridge, B on a bridge convex upward and C goes on a bridge concave upward. Let FA, FB and FC be the normal forces exerted by the car on the bridges when they are at the middle of bridges.
(a) FA is maximum of the three forces.
(b) FB is maximum of the three forces.
(c) FC is maximum of the three forces.
(d) FA = FB = FC.
Answer-11:-
The option (c) FC is maximum of the three forces. is correct
Explanation:
At the middle of bridge, normal force can be given as :
![]()
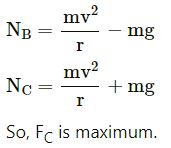
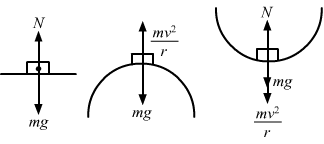
Question-12 :-
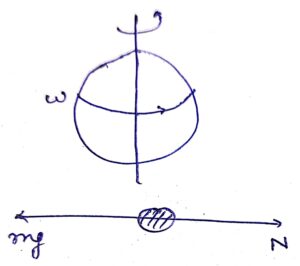
A train A runs from east to west and another train B of the same mass runs from west to east at the same speed along the equator. A presses the track with a force F1 and B presses the track with a force F2.
(a) F1 > F2.
(b) F1 < F2
(c) F1 = F2
(d) the information is insufficient to find the relation between F1 and F2.
Answer-12 :-
The option (a) F1 > F2. is correct
Explanation:
Earth rotates about its axis from west to east.
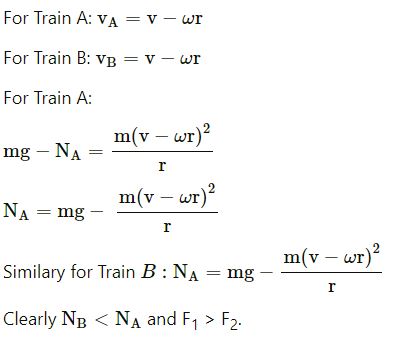
Question-13 :-
If the earth stop rotating, the apparent value of g on its surface will
(a) increase everywhere
(b) decrease everywhere
(c) remain the same everywhere
(d) increase at some places and remain the same at some other places.
Answer-13 :-
The option (a) increase at some places and remain the same at some other places. is correct
Explanation:
If the Earth stops rotating on its axis, there will be an increase in the value of acceleration due to gravity at the equator. At the same time, there will be no change in the value of g at the poles.
Question-14 :-
A rod of length L is pivoted at one end and is rotated with a uniform angular velocity in a horizontal plane. Let T1 and T2 be the tensions at the points L/4 and 3L/4 away from the pivoted ends.
(a) T1 > T2
(b) T2 > T1
(c) T1 = T2
(d) The relation between T1 and T2 depends on whether the rod rotates clockwise or anticlockwise.
Answer-14 :-
The option (a) T1 > T2 is correct
Explanation:
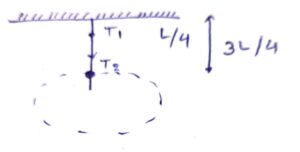
Let the angular velocity of the rod be ω .
Distance of the centre of mass of portion of the rod on the right side of L/4 from the pivoted end :

Mass of the rod on the right side of L/4 from the pivoted end : ![]()
At point L/4, we have :
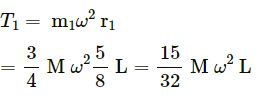
Distance of the centre of mass of rod on the right side of 3L/4 from the pivoted end :
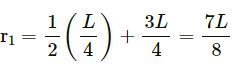
Mass of the rod on the right side of L/4 from the pivoted end :
At point 3L/4, we have :
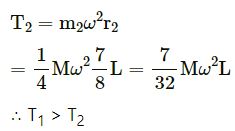
Question-15 :-
A simple pendulum having a bob of mass m is suspended from the ceiling of a car used in a stunt film shooting. the car moves up along an inclined cliff at a speed v and makes a jump to leave the cliff and lands at some distance. Let R be the maximum height of the car from the top of the cliff. The tension in the string when the car is in air is
(a) mg
(b) mg−mv²/R
(c) mg+mv²/R
(d) zero.
Answer-15 :-
The option (d) zero. is correct
Explanation:
When the car is in air, the acceleration of bob and car is same. Hence, the tension in the string will be zero.
Question-16 :-
Let θ denote the angular displacement of a simple pendulum oscillating in a vertical plane. If the mass of the bob is m, the tension is the string is mg cos θ
(a) always
(b) never
(c) at the extreme positions
(d) at the mean position.
Answer-16 :-
The option (c) at the extreme positions. is correct
Explanation:
at the extreme positions
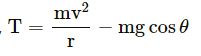
When v = 0,
|T| = mg cosθ
That is, at the extreme positions, the tension is the string is mg cosθ.
—: End of Ch-7 Circular Motion Obj-1 (MCQ-1) HC Verma Solutions Vol-I :–
Return to — HC Verma Solutions Vol-1 Concept of Physics
Thanks



Thank you soo much icsehelp.com helped me alot I think this the best app for the student Thanks alot 😊 😊 🙏🏻🙏🏻👍👍👏👏