Complex Numbers Class 11 OP Malhotra Exe-9B ISC Maths Solutions Ch-9

Complex Numbers Class 11 OP Malhotra Exe-9B ISC Maths Solutions Ch-9. In this article you would learn about Operation and Properties with Complex Number. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Complex Numbers Class 11 OP Malhotra Exe-9B ISC Maths Solutions Ch-9

Board	ISC
Publications	S Chand
Subject	Maths
Class	11th
Chapter-9	Complex Numbers
Writer	O.P. Malhotra
Exe-9(B)	Operation and Properties of Complex Number.

Exercise- 9B

Complex Number Class 11 OP Malhotra Exe-9B Solution.

Que-1: In each of the following find r + s, r – s, rs, r/s if r denotes the first complex number and s denotes the second complex number :
(i) 3 + 7i, i
(ii) – i, 5 + 2 i
(iii) 3i, 1 – i
(iv) – 7, – 1 – 3i
(v) 7 + 3i, 3i – 7

Sol: (i) Given r = 3 + 7i and s = i
∴ r + s = 3 + 7i + i = 3 + 8i;
rs = (3 + 7i) i = 3i + 7i² = 3i – 7
r – s = 3 + 7i – i = 3 + 6i;
r/s = (3+7i)/i × (i/i)
= (3i−7)/−1
= 7 – 3 i

(ii) Given r = – i; s = 5 + 2i
∴ r + s = – i + 5 + 2i = 5 + i;
r – s = – i – 5 – 2i = – 5 – 3i
r . s = – i (5 + 2i) = – 5i – 2i² = – 5i + 2
r/s = −i/(5+2i) × (5−2i)/(5−2i)
= {−i(5−2i)}(5²−(2i)²)
= (−5i−2)/(25+4)
= (−5/29i) − (2/29)

(iii) Given r = 3i and s = 1 – i
∴ r + s = 3i + 1 – i = 1 + 2i;
r – s = 3i – 1 + i = 4i – 1
rs = 3i (1 – i) = 3i – (- 3) = 3i + 3
r/s = (3i/1−i) × (1+i)/(1+i)
= {3i(1+i)}/(1²−i²)
= (3i+3i²)/(1+1)
= (3i/2) − (3/2)

(iv) Given r = – 7 and s = – 1 – 3i
∴ r + s = – 7 – 1 – 3i = – 8 – 3i;
r – s = – 7 + 1 + 3i = – 6 + 3i
rs = – 7 (- 1 – 3i) = 7 + 21i
and r/s = {−7/(−1−3i)}
= (7/3i+1) × (3i−1)/(3i−1)
= {7(3i−1)}/(−9−1)
= (21i−7)/−10
= (−21i/10) + (7/10)

(v) Given r = 7 + 3i; s = 3i – 7
∴ r + s = 7 + 3i + 3i – 7 = 6i;
r – s = 7 + 3i – 3i + 7 = 14
rs = (7 + 3i) (3i – 7) = (3i)² – 7²
= – 9 – 49 = – 58
r/s = (7+3i)/(3i−7) × (3i+7)/(3i+7)
= {(3i+7)²}/(−9−49)
= (−9+49+42i)/−58
= (40+42i)/−58
= (−20/29) − (21/29) i

Que-2: Solve each of the following equations for real x and y :
(i) (x + y) + (3 – 2i) = 1 + 4i
(ii) (x + yi) – (7 + 4i) = 3 – 5i
(iii) 2x + yi = 1 + (2 + 3i)
(iv) x + 2yi = i – (- 3 + 5i)

Sol: (i) Given, (x + yi) + (3 – 2i) = 1 + 4i
⇒ (x + 3) + i (y – 2) = 1 + 4i
On comparing real and imaginary parts on both sides ; we have
x + 3 = 1 ⇒ x = – 2
y – 2 = 4 ⇒ y = 6

(ii) Given (x + yi) – (7 + 4i) = 3 – 5i
⇒ (x – 7) + i (y – 4) = 3 – 5i
On comparing real and imaginary parts on both sides ; we have
x – 7 = 3 ⇒ x = 10
and y – 4 = – 5 ⇒ y = – 1

(iii) Given 2x + yi = 1 + (2 + 3i)
⇒ 2x + yi = 3 + 3i
On comparing real and imaginary parts on both sides, we have
2x = 3 ⇒ x = 3/2 and y = 3

(iv) Given x + 2yi = i – (- 3 + 5i) = i + 3 – 5i
⇒ x + 2yi = 3 – 4i
On comparing real and imaginary parts on both sides,
x = 3 and 2y = – 4 ⇒ y = – 2

Que-3: Determine the conjugate and the reciprocal of each complex number given below :
(i) i
(ii) i³
(iii) 3 – i
(iv) √-1 − 3
(v) √-9 − 3

Sol: (i) Conjugate of i = i = – i
and Reciprocal of i = 1/i
= −i²/i =  – i

(ii) Conjugate of i³ = i³ = (- i)³ = – i³
= – i² x i = i
and Reciprocal of i³ = 1/i³
= (1/−i) × (i/i)
= i/−i² = i

(iii) Conjugate of (3 – i) = 3−i = 3 + i

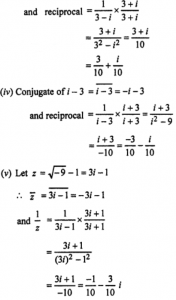
Que-4: Simplify :
(i) (3 – 7i)²
(ii) ((−1/2) − (√3i/2))²
(iii) (9 + 4i) ((3/2) – i ) (9 – 4i)

Sol: (i) (3 – 7i)² = 3² x (7i)² – 42i
= 9 – 49 – 42i
= – 40 – 42i

(ii) [(−1/2) − (√3i/2)]²
= (−1/2)² + (−√3i/2)² + √3i/2
= (1/4) + (3i²/4) + (√3i/2)
= (1/4) − (3/4) + (√3i/2)
= (−1/2) + (√3i/2)

(iii) (9 + 4i) ((3/2) – i) (9 – 4i)
= (9 + 4i) (9 – 4i) ((3/2) – i)
= [81 – (4i)²]((3/2) – i)
= (81 + 16) ((3/2) – i)
= 97((3/2) – i) = 291/2 – 97i

Que-5: Determine real values of x and y for which each statement is true.
(i) {(x+y)/i} + x – y + 4 = 0
(ii) – (x + 3y)i + (2x – y + 1) = 8/i
(iii) (x – yi) = (2+i)/(1+i)
(iv) (3 – 4i) + (x + yi) = 1 + 0i
(v) (x – yi)(2 + 3i) = (x−2i)/(1−i)
(vi) (x4 + 2xi) – (3x² + yi) = (3 – 5i) + (1 + 2yi)

Sol: (i) Given {(x+y)/i} + x – y + 4 = 0
⇒ (x + y) + i (x – y + 4) = 0 = 0 + i0
On comparing real and imaginary parts on both sides ; we have
x + y = 0 …(1)
and x – y = – 4 …(2)
On adding eqn. (1) and (2); we have 2x = – 4
⇒ x = – 2 from (1) ; y = 2

(ii) Given – (x + 3y) i + (2x – y + 1) = 8/i
⇒ (x + 3y) + (2x – y + 1) i = 8 [∵ i² = – 1]
On comparing real and imaginary parts on both sides ; we have
x + 3y = 8 …(1)
2x – y = – 1 …(2)
eqn. (1) + 3 x eqn. (2); we have
7x = 5 ⇒ x = 5/7
∴ from (1); (5/7) + 3y =8
⇒ 3y = 8 – (5/7) = 51/7
⇒ y = 17/7

(iii) Given (x – yi) = (2+i)/(1+i) × (1−i)/(1−i)
= {(2+i)(1−i)}/(1²−i²)
⇒ (x – yi) = (2−2i+i+1)/(1+1) = (3−i)/2
= (3/2) – (i/2)
On comparing real and imaginary parts on both sides; we have
x = 3/2 and – y = –1/2 ⇒ y = 1/2

(iv) Given (3 – 4i) (x + iy) = 1 + 0i
⇒ x + iy = {1/(3−4i)} × (3+4i)/(3+4i)
= (3+4i)/(3²−(4i)²)
⇒ x + iy = (3+4i)/(9+16)
= (3/25) + (4/25)i
On comparing real and imaginary parts on both sides ; we have
x = 3/25 and y = 4/25

(v) Given (x – yi) (2 + 3i) = (x−2i)/(1−i)
⇒ (x – yi) (2 + 30 (1 – i) = x – 2i
⇒ (x – yi) (2 – 2i + 3i + 3) = x – 2i
⇒ (x – yi) (5 + i) = x – 2i
⇒ 5x + xi – 5yi + y = x – 2i
On comparing real and imaginary parts on both sides ; we have
5x + y = x ⇒ 4x + y = 0 …(1)
x – 5y = – 2 …(2)
∴ from (1) ; y = -4x
∴ from (2); x + 20x = – 2 ⇒ x = −2/21
∴ from (1) ; y = – 4x = 8/21

(vi) Given
(x⁴ + 2xi) – (3x² + yi) = (3 – 5i) + 1 + 2yi
⇒ (x⁴ – 3x²) + i (2x – y) = 4 + (2y – 5) i
On comparing real and imaginary parts on both sides, we have
x⁴ – 3x² = 4
⇒ x⁴ – 3x² – 4 = 0
⇒ (x² – 4) (x² + 1) = 0
⇒ x = ± 2, ± i
Since x, y ∈ R ⇒ x = ± 2
Also 2x – y = 2y – 5 ⇒ 2x – 3y = – 5 …(1)
When x = 2
∴ from (1); 4 – 3y = – 5 ⇒ y = 3
When x = – 2
∴ from(1) ; – 4 – 3y = – 5 ⇒ y = 1/3

Que-6: Write the conjugate of (6 + 5i)².

Sol: Let z = (6 + 5i)² = 36 – 25 + 60i = 11 + 60i
∴ z = 11+60i = 11 – 60i

Que-7: Write the additive inverse of the following:
(i) – 2 + 3 i
(ii) 3 – 4i

Sol: (i) Let z = – 2 + 3i
∴ additive inverse of z = – z
= -(-2 + 3i)
= 2 – 3i

(ii) Let z = 3 – 4i
∴ additive inverse of z = – z = – (3 – 4i)
= – 3 + 4i

Que-8: Find the multiplicative inverse of each of the following complex numbers when it exists.
(i) 2 + 2i
(ii) 0 + 0i
(iii) – 7 + 0i
(iv) – 16
(v) i/(1+i)
(vi) (1 +1)²
(vii) (3+4i)/(4−5i)
(viii) (6 + 5i)²
(ix) {(2+3i)(3+2i)i}/(5+i)

Sol: (i) Let z = 2 + 2i
∴ Multiplicative inverse of z = 1/z
= {1/(2+2i)} × (2−2i)/(2−2i)
= (2−2i)/(2²−(2i)²)
= (2−2i)/(4+4)
= (2−2i)/8
= (1/4) − (i/4)

(ii) Let z = – 7 + 0i = – 7
∴Multiplicative inverse of z = 1/z
= –1/7 = –1/7 + 0i

(iii) Let z = 0 + 0i = 0
∴ Multiplicative inverse of z does not exists, since z = 0

(iv) Let z = – 16
∴ Multiplicative inverse of z = 1/z
= 1/(-1/6) = (−1/16) + 0i

(v) Let z = i/(1+i)
∴ Multiplicative inverse of z = 1/z
= 1/z
= – i + 1 = 1 – i

(vi) Let z = (1 + i)² = 1 + i2 + 2i
= 1 – 1 + 2i = 2i
∴ Multiplicative inverse of z = 1/z
= (1/2i) × (i/i)
= (i/2i²) = i/−2 = 0 – (1/2)i

(vii) Let z = (3+4i)/(4−5i)
∴ Multiplicative inverse of z = 1/z

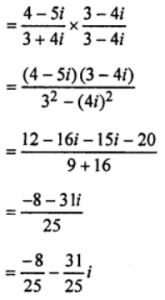
(viii) Let z = (6 + 5i)² = 36 – 25 + 60i = 11 + 60i
∴ Multiplicative inverse of z = 1/z

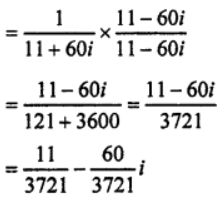
(ix) Let z = {(2+3i)(3+2i)i}/(5+i)
= {(2i−3)(2i+3)}/(5+i)
= {(2i)²−3²)/(5+i)
⇒ z = (−4−9)/(5+i)
= −13/(5+i)
∴ Multiplicative inverse of z = 1/z
= (5+i)/−13
= (−5/13) − (1/13)i

Que-9: Simplify :
(i) (1 + i)¯¹
(ii) √(-49/25) √(-1/9)
(iii) √-64 ⋅ (3+√-361)
(iv) (3 – 7i)²
(v) ((−1/2) − (√3/2)i)²
(vi) {(1−i)³+/(1−i³)
(vii) {(1+i)/(1−i)}^(4n+1) (n, is a + ve integer)
(viii) {√(5+12i)+√(5-12i)}/{√(5+12i)-√(5-12i)}

Sol: (i) (1 + i)¯¹ = (1/(1+i)) × (1−i)/(1−i)
= (1−i)/(1²−i²) = (1−i)/2
= (1/2) − (i/2)

(ii) √(-49/25) √(-1/9) = (7i/5)(1i/3)
= (7/15)i² = – 7/15

(iii) √-64 ⋅ (3+√-361) = 8i (3 + 19i)
= 24i + 152i² = 24i – 152

(iv) (3 – 7i)² = 3² + (7i)² – 42i
= 9 – 49 – 42i = – 40 – 42i

(v) ((−1/2) − (√3/2i)² = {(1/2) + (√3/2i)}²
= (1/2)² + (√3/2i)² + 2×(1/2)×(√3/2i)
= (1/4) − (3/4) + (√3/2i) = (−1/2) + (√3/2i)

(vi) {(1−i)³}/(1−i³) = {1³−i³−3i(1−i)}/(1−i²×i)
= (1+i−3i−3)/(1+i) = (−2−2i)/(1+i)
= {−2(1+i)/(1+i) = – 2

(vii) {(1+i)/(1−i)}^(4n+1) = [{(1+i)/(1−i)} × {(1+i)/(1+i)}]^(4n+1)
= [{(1+i)²/(1²−i²)]^(4n+1) = [(1+i²+2i)/(1+1)]^(4n+1)
= [(1−1+2i)/2]^(4n+1) = i^(4n+1)
= i^4n, i = (i^4)^n x i = 1^n x i = i

(viii) 5 + 12i = 9 – 4+ 12i
= 3² + (2i)² + 2 x 3 x 2i
= (3 + 2i)²
and 5 – 12i = 9 – 4 – 12i
= 3² + (2i)² – 2 x 3 x 2i
= (3 – 2i)²
∴ {√(5+12i) +√(5−12i)}/{√(5+12i)−√(5−12i)} = [√(3+2i)²+√(3−2i)²]/[√(3+2i)²-√(3−2i)²]
= (3+2i+3−2i)/(3+2i−(3−2i))
= 6/4i = (3/2i) × (i/i)
= (3i/−2) = – 3/2i

Que-10: Prove that [{(3+2i)/(2−5i)}+{(3−2i)/(2+5i)}] is rational.

Sol: Given : [{(3+2i)/(2−5i)}+{(3−2i)/(2+5i)}]

which is a rational number

Que-11: Show that (1+2i)/(3+4i) × (1−2i)/(3−4i) is real.

Sol: (1+2i)/(3+4i) × (1−2i)/(3−4i)
= {1²−(2i)²}/(3²−(4i)²)
= (1+4)/(9+16) = 5/25 = 1/5
which is clearly a real number.

Que-12: Perform the indicated operation and give your answer in the form x + yi, where x and y are real numbers and i = √-1.
(i) (3 + 4i)¯¹
(ii) (2−√-25)/(1−√-16)
(iii) (5+2i)/(−1+√3i)
(iv) (5−3i)/(6+i)
(v) (√5−7i)(√5−7i)²+(−2+7i)²

Sol: (i) (3 + 4i)¯¹
= {1/(3+4i)} × (3-4i)/(3-4i)
= (3-4i)/(3²-(4i)²)
= (3-4i)/(9+16)
= (3/25) – (4/25)i

(ii) (2−√-25)/(1−√-16)

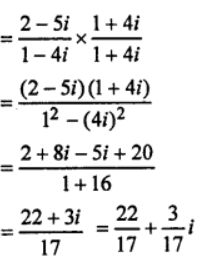
(iii) (5+2i)/(−1+√3i)

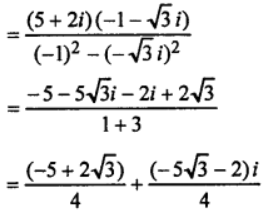
(iv) (5−3i)/(6+i)

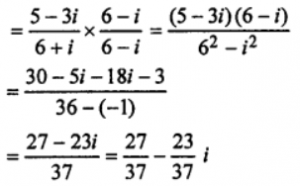
(v) (√5−7i)(√5−7i)²+(−2+7i)²

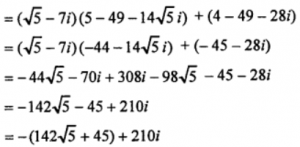
Que-13: If x + yi = (u+vi)/(u−vi) prove that x² + y² = 1.

Sol: Given x + iy = u+viu−vi
Taking modulus on both sides; we have
|x + iy| = ∣∣ (u+vi)/(u−vi) ∣∣ = |(u+vi)| / |u−vi| [∵ ∣∣ z1/z2 ∣∣ = |z1| / |z2| ]
⇒ √(x²+y²) = {√(u²+v²)} / {√(u²+(-v²))
⇒ √(x²+y²) = 1
On squaring both sides ; we have
x² + y² = 1

Que-14: Prove that:  [4+3√-20]^(1/2) + [4−3√-20]^(1/2) = 6.

Sol: We have the expression: [4 + 3√(-20)]^(1/2) + [4 – 3√(-20)]^(1/2)
First, let’s simplify the square roots:
√(-20) = √(20) * √(-1) = 2√5 * i, where i is the imaginary unit.
Now we can substitute this value back into the expression:
[4 + 3√(-20)]^(1/2) + [4 – 3√(-20)]^(1/2)
= [4 + 3 * 2√5 * i]^(1/2) + [4 – 3 * 2√5 * i]^(1/2)
= [4 + 6√5 * i]^(1/2) + [4 – 6√5 * i]^(1/2)
Let’s define a = 4 + 6√5 * i and b = 4 – 6√5 * i.
If z = x + yi, where x and y are real numbers, the square root of z is given by:
√z = ±(√[(x + r)/2] + i * sgn(y) * √[(r – x)/2])
For a = 4 + 6√5 * i:
Magnitude r = √(4^2 + (6√5)^2) = √(16 + 180) = √196 = 14
√a = ±(√[(4 + 14)/2] + i * sgn(6√5) * √[(14 – 4)/2])
= ±(√9 + i * sgn(6√5) * √5)
= ±(3 + i * √5)
Similarly, for b = 4 – 6√5 * i:
Magnitude r = √(4^2 + (-6√5)^2) = √(16 + 180) = √196 = 14
√b = ±(√[(4 + 14)/2] + i * sgn(-6√5) * √[(14 – 4)/2])
= ±(√9 – i * √5)
= ±(3 – i * √5)
Now we substitute the values back into the expression:
√a + √b = (3 + i * √5) + (3 – i * √5)
= 3 + i * √5 + 3 – i * √5
= 6
Therefore, the expression [4 + 3√(-20)]^(1/2) + [4 – 3√(-20)]^(1/2) simplifies to 6.

Que-15: Express the following in the form a + bi :
(i) √[{5(2+i)}/(2-i)]
(ii) (3−i)²/(2+i)
(iii) (1 + i)¯³
(iv) {(4i³−i)/(2i+1)}²
(v) (i−1)/(i+1)
(vi) (2+i)/{(3−i)(1+2i)}
(vii) 5/(2i−7i²)

Sol: (i) √[{5(2+i)}/(2-i)]
= √{5(2+i)}/(2-i) × (2+i)/(2+i)
= √{5(2+i)²}/(2²-i²)
= √{5(2+i)²}/(4+1)
= 2 + i

(ii) (3−i)²/(2+i)
= (9-1-6i)/(2+i)
= (8-6i)/(2+i) × (2-i)/(2-i)
= {(8-6i)(2-i)}/(2²-i²)
= (16-8i-12i-6)/(4+1)
= (10-20i)/5
= 2 – 4i

(iii) (1 + i)¯³

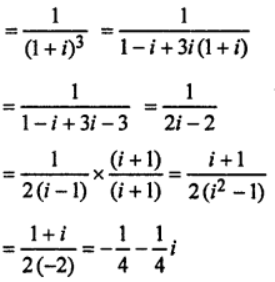
(iv) {(4i³−i)/(2i+1)}²

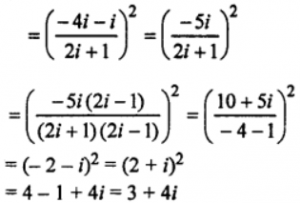
(v) (i−1)/(i+1)
= {(i-1)(i-1)}/{(i+1)(i-1)}
= (i-1)²/(i²-1²)
= (-1+1-2i)/(-1-1)
= i

(vi) (2+i)/{(3−i)(1+2i)}
= (2+i)/(3+6i-i+2)

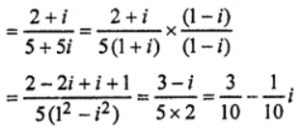
(vii) 5/(2i−7i²)
= {5/(2i+7)} × (2i-7)/(2i-7)

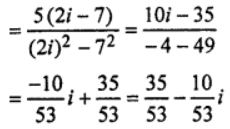
Que-16: Prove that {(−1+i√3)/2}³ is a positive integer.

Sol: {(−1+i√3)/2}³
= (1/8) [(−1)³+(i√3)³−3√3i (−1+i√3)]
= (1/8) [−1−3√3i+3√3i+9] = 8/8 = 1
which is a positive integer.

Que-17: If one of the values of x of the equation 2x² – 6x + k = 0 be (1/2) (a + 5i), find the values of a and k.

Sol: Given eqn. be 2x² – 6x + k = 0
⇒ x = {6±√(36-8k)}/4 = {6±2√(9-2k)}/4
⇒ x = {3±√(9-2k)}/2
Since one of the values of x is given to be (1/2) (a + 5i) which is only possible
if 9 – 2k = – 25 ⇒ 2k = 34 ⇒ k = 17
∴ x = (3±5i)/2 = (1/2) (3±5i)
Hence required value of a be 3.

Que-18: Define conjugate complex numbers and show that their sum and product are real numbers.

Sol: Let z = x + iy be any complex number where x, y ∈ R
Then conjugate of z = z = (x + iy)¯
= x – iy
∴ z + z¯ = x + iy + x – iy = 2x, which is a real number
and zz¯ = (x + iy) (x – iy) = x² – (i y)²
= x² + y²
which is again a real number, since x and y are reals.

Que-19: If z¯ = – z ≠ 0, show that z is necessarily a purely imaginary number.

Sol: Let z = x + iy where x, y ∈ R, x, y are not both zero.
∴ z¯ = x – iy
Also, given z¯ = – z
⇒ x – iy = – (x + iy)
⇒ x – iy = – x – iy
⇒ 2x = 0 ⇒ x = 0
∴ z = iy which is purely an imaginary number.

Que-20: z and z’ are complex numbers such that their product zz’ = 3 – 4i.
Given that z’ is 5 + 3i, express z in the form a + bi where a and b are rational numbers

Sol: Given z, z’ ∈ C
s.t zz’ = 3 – 4z …(1)
Also, z’ = 5 + 3z
∴ from (1); we have
z = (3−4i)/(5+3i) × (5−3i)/(5−3i) = {(3−4i)(5−3i)}/(5²−(3i)²)
⇒ z = (15−9i−20i−12)/(25+9) = (3−29i)/34
⇒ z = (3/34) − (29/34) i

Que-21: If a + bi = (x+i)²/(2x²+1), prove that a² + b² = (x²+1)²/(2x²+1)².

Sol: Given : a + bi = (x+i)²/(2x²+1)
Taking modulus on both sides ; we have

Que-22: Let z1 = 2 – i, z2 = – 2 + i, find
(i) Re (z1.z2)/(z¯1),
(ii) Im (1/(z1.z¯2))

Sol: Given z1 = 2 – i, z2 = – 2 + i.

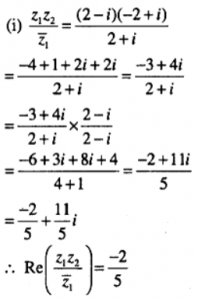
(ii) 1/z1.z1¯
= 1/{(2-i)(2+i)}
= 1/(1+4)
= 1/5 + i0
Im (1/z1.z1¯) = 0.

Que-23: If z1 = 3 + 5i and z2 = 2 – 3i, then verify that (z1/z2)¯ = z¯1 / z¯2.

Sol: Given : z₁ = 3 + 5i and z₂ = 2 – 3i
z1/z2 = (3+5i)/(2-3i) × (2+3i)/(2+3i)
= (6+9i+10i-15)/(2²+9)
= (-9+19i)/13
= (-9/13) + (19/13)i
(z1/z2)¯ = (-9/13) – (19/13)i   ,….. (1)

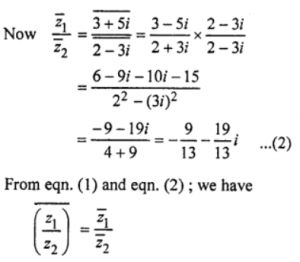
Que-24If x = – 2 – √3i, where i = √-1m, find that value of 2×4 + 5x³ + 7x² – x + 41.

Sol: Given x = – 2 – √3i
⇒ x + 2 = – √3i
On squaring both sides ; we have
(x + 2)² = (- √3i)² ⇒ x² + 4x + 4 = – 3
⇒ x² + 4x + 7 = 0 … (1)
Now 2×4 + 5x³ + 7s2 – x + 41 = 2x² (x² + 4x + 7) – 3x³ – 7x² – x + 41
= 2x² (x² + 4x + 7) – 3x (x² + 4x + 7) + 5x² – 20x + 41
= 2x² (x² + 4x + 7) – 3x (x² + 4x + 7) + 5 (x² – 4x + 7) + 6
= 2x² x 0 – 3x × 0 + 5 x 0 + 6
= 6 [using (1)]

Que-25: If z = – 3 + √-2, then prove that z4 + 5z³ + 8z² + 7z + 4 is equal to – 29.

Sol: Given z = – 3 + √-2 = – 3 + √-2 i
⇒ z + 3 = √-2 i; On squaring both sides ; we have
(z + 3)² = (√-2 i)² ⇒ z² + 6z + 9 = – 2
⇒ z² + 6z+ 11 =0 …(1)
∴ z4 + 5z³ + 8z² + 7z + 4 = z² (z² + 6z + 11) – z³ – 3z² + 7z + 4
= z²(z² + 6Z+ 11) – z (z² + 6z + 11) + 3z² + 18z + 4
= z² (z² + 6z + 11) – z (z² + 6z + 11) + 3 (z² + 6z + 11) – 29
= z² x 0 – z x 0 + 3 x 0 – 29 [using eqn. (1)]
= – 29

–: End of Complex Numbers Class 11 OP Malhotra Exe-9B ISC Maths Ch-9 Solutions. :–

Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions

Thanks

Please share with your friends