Compound and Multiple Angles Class 11 OP Malhotra Exe-5D ISC Maths Solutions

Compound and Multiple Angles Class 11 OP Malhotra Exe-5D ISC Maths Solutions Ch-5 Solutions. In this article you would learn about Extra Questions on Proving. Step by step solutions of latest textbook has been given as latest syllabus. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

Compound and Multiple Angles Class 11 OP Malhotra Exe-5D ISC Maths Solutions Ch-5

Board	ISC
Publications	S Chand
Subject	Maths
Class	11th
Chapter-5	Compound and Multiple Angles
Writer	OP Malhotra
Exe-5(D)	Extra Questions on Proving.

Exercise- 5D

Compound and Multiple Angles Class 11 OP Malhotra Exe-5D Solution.

Que-1: (i) (sin Φ – cos Φ)² = 1 – sin²Φ.
(ii) (cos(θ/2)+sin(θ/2))² = 1 + sin θ.

Sol: (i) (sin Φ – cos Φ))²
= sin² Φ + cos² Φ – 2 sin Φ cos Φ
= 1 – sin 2Φ

(ii) (cos(θ/2)+sin(θ/2))²
= cos²(θ/2) + sin²(θ/2) + 2sin(θ/2) cos(θ/2
= 1+sin(2⋅(θ/2))
= 1 + sinθ

Que-2: {sinθ×tan(θ/2)}/2 = sin²(θ/2)

Sol: {sinθ tan(θ/2)}/2
= {2sin(θ/2) cos(θ/2) tan(θ/2)}/2
= sin² (θ/2)

Que-3: 1/sec 2θ = cos^4 θ − sin^4 θ

Sol: LHS = 1/sec 2θ
= cos 2θ = (cos² θ – sin² θ) . 1
= (cos² θ – sin² θ) (cos² θ + sin² θ)
= cos⁴ θ – sin⁴ θ

Que-4: 2/(cotα tan2α) = 1 – tan² α.

Sol: 2/(cotα tan2α)
= 2tanα / tan2α
= 2tanα/{2tanα/(1−tan2α)}
= 1 – tan² α

Que-5: sin2A/(1−cos2A) = cot A

Sol: sin2A/(1−cos2A)
= {2sinA cosA}/2sin²A
= cot A

Que-6: sin2A/(1+cos2A) = tan A

Sol: sin2A/(1+cos2A)
= (2sinA cosA)/2cos²A
= tan A

Que-7: (sin3θ/sinθ) − (cos3θ/cosθ) = 2

Sol: LHS = (sin3θ/sinθ) − (cos3θ/cosθ)
= {sin 3θ cos θ – sin θ cos 3θ} / (sin θ cos θ)
= {sin (3θ-θ)}/(sin θ cos θ)
= sin 2θ/(sinθ cosθ)
= (2sinθ cosθ)/(sinθ cosθ)
= 2.

Que-8: (cos³A−sin³A)/(cosA−sinA) = (2+sin2A)/2.

Sol: LHS = (cos³A−sin³A)/(cosA−sinA)
= {(cosA – sinA)(cos²+sin²A+cosA sinA)}
= cos²A + sin²A + cosA sinA = 1 + (1/2) (2sinA cosA)
= 1 + (sin2A/2)
= (2+sin2A)/2  =  RHS.

Que-9: (1−cos2θ)/sin2θ = tan θ.

Sol:  L.H.S = (1−cos2θ)/sin2θ
= 2sin²θ/(2sinθ cosθ)
= tan θ = R.H.S

Que-10: cot α – tan α = 2 cot 2α.

Sol: L.H.S = cot α – tan α = (1/tanα) − tanα
= (1−tan²α)/tanα
= {2(1−tan²α)}/2tanα
= 2/{(2tanα)/(1−tan²α)} = 2tan²α
= 2 cot 2α = R.H.S

Que-11: cosec A – 2 cot 2A cos A = 2 sin A.

Sol: L.H.S = cosec A – 2 cot 2A cos A
= (1/sinA) – 2[{(cos2A/sin2A)cos2A}]
= (1/sinA) – 2[{(cos²A-sin²A)/(2sinA cosA)}cosA]
= (1/sinA) – 2[{(cos²A-sin²A)}/sinA]
= [1 – (cos²A-sin²A)]/sinA
= [1 – (cos²A+sin²A)]/sinA
= 2sin²A/sinA
= 2 sin A = R.H.S

Que-12: {1 + sin2x + cos2x}/(cosx + sinx) = 2cosx

Sol: LHS = {1 + sin2x + cos2x}
– sin2x = 2sinx cosx
– cos2x = cos2x − sin2x
– 1 = sin2x + cos2x
Substituting these identities into the LHS gives:
1 + sin2x + cos2x = (sin²x+cos²x) + (2sinx cosx) + (cos²x − sin²x).
1 + sin²x + cos²x = sin²x + cos²x + 2sinx cosx + cos²x − sin²x.
= 2cos²x + 2sinx cosx.
= 2(cos²x + sinx cosx).
= 2(cos²x+sinx cosx) / cosx + sinx
= {2cosx (cosx+sinx)} / (cosx + sinx)
= 2 cosx

Que-13: {1-cos2x+sinx}/(sin2x+cosx) = tanx

Sol: LHS = {1-cos2x+sinx}/(sin2x+cosx)
= (2sin²x+sinx)/(2sinx cosx + cosx)
= {sinx(2sinx+1)}/{cosx(2sinx+1)}
= sinx/cosx
= tanx = RHS.

Que-14: (sinθ+sin2θ)/(1+cosθ+cos2θ) = tanθ

Sol: LHS = (sinθ+sin2θ)/(1+cosθ+cos2θ)
= (sinθ+2sinθcosθ)/(1+cosθ+2cos²θ-1)
= {sinθ(1+2cosθ)}/{cosθ(1+2cosθ)}
= sinθ/cosθ
= tanθ = RHS.

Que-15: cotA = (1/2) [cot(A/2)-tan(A/2)]

Sol: RHS = (1/2) [cot(A/2)-tan(A/2)]

= cosA/sinA
= cotA = LHS.

Que-16: {(cosA+sinA)/(cosA-sinA)} – {(cosA-sinA)/(cosA+sinA)} = 2tan 2A

Sol: Taking LHS

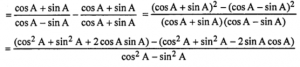
= (4sinA cosA)/cos 2A
= 2sin 2A/cos 2A
= 2tan 2A = RHS.

Que-17: {(cosA-sinA)/(cosA+sinA)} = sec 2A – tan 2A

Sol: R.H.S = sec 2A – tan 2A
= (1/cos2A) − (sin2A/cos2A)
= (1−sin2A)/cos2A
= {cos²A+sin²A−2sinAcosA}/(cos2A−sin2A)
= {(cosA−sinA)²}/{(cosA−sinA)(cosA+sinA)}
= (cosA−sinA)/(cosA+sinA) = L.H.S

Que-18: {sin 2A/(1-cos 2A)} . {(1-cosA)/cosA} = tan A/2

Sol: LHS = {sin 2A/(1-cos 2A)} . {(1-cosA)/cosA}
= {(2sinA cosA)/2sin²A} . {2sin²(A/2)}/cosA
= {2sin²(A/2)}/{2sin(A/2) cos(A/2)}
= tan (A/2) = RHS.

Que-19: 2 cos A = √[2+√{2(1+cos4A)}], A ∈ I or IV Quad.

Sol: RHS = √[2+√{2(1+cos4A)}]
= √[2+√{2(1+2cos² 2A)}]
= √{2+2cos 2A} = √[2{1+cos 2A}]
= √{2.2cos² A}
= 2cos A.

Que-20: tan 2A = √{sec²-1}, A in I or IV Quad.

Sol: R.H.S = √{sec²-1}
= {(1/cos2A)+1} tanA
= {(1+cos2A)/cos2A} ⋅ tanA
= (2cos²A⋅tanA) / (cos²A−sin²A)
= {2tanA cos²A}/[cos²A[1−tan²A]]
= 2tanA/(1−tan2A)
= tan 2A = L.H.S

Que-21: (sec8A−1)/(sec4A−1) = tan8A/tan2A .

Sol:  LHS = (sec8A−1)/(sec4A−1)
= {(1/cos 8A)-1}/{(1/cos 4A)-1}
= {(1-cos 8A)/(1-cos 4A)} × {(cos 4A)/(cos 8A)}
= {(2sin² 4A)/(2sin² 2A)} . {(cos 4A)/(cos 8A)}
= {(2sin 4A cos 4A)sin 4A}/{cos 8A (2sin² 2A)}
= (sin 8A sin 4A)/(cos 8A 2sin² 2A)
= {tan 8A (2sin 2A cos 2A)}/2sin² 2A
= tan 8A . cot 2A
= tan 8A/tan 2A = RHS.

Que-22: tan 2A – sec A sin A = tan A sec 2 A.

Sol: LHS = tan 2A – sec A sin A
= tan 2A – (sinA)/cosA
= tan 2A – tan A
= [{2tan A}/{1-tan²A}] – tanA

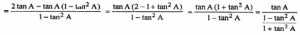
= tan A/cos 2A
= tan A sec 2A = RHS

Que-23: (i) (cos A + cos B)² + (sin A + sin B)² = 4 cos² (A−B)/2.
(ii) (cos A – cos B)² + (sin A – sin B)² = 4 sin² (A−B)/2.

Sol:  (i)  LHS = (cos a+cosb)² + (sina-sinb)²
= Cos²a + Cos²b + 2CosaCosb + Sin²a + Sin²b – 2SinaSinb
= 2 + 2(CosaCosb – SinaSinb)
= 2 + 2Cos(a+b)
= 2 ( 1 + Cos(a+b))
= 2* 2Cos²(a+b/2)  (∵ 2Cos²θ/2 = 1 + Cosθ)
= 4 Cos²(a+b/2)
= R.H.S
Hence proved

(ii) L.H.S,= { cosA – cosB }^2 + {sinA -sinB}^2
[sinC-sinD= 2cosC+D)/2 sin(C-D)/2&cosC-cosD=2sin(C+D)/2sin(D-C)…
= { 2 sin(A+B)/2 sin(B- A)/2}^2 + { 2cos(A+B)/2 sin(A-B)/2}^2
=4 sin^2(A-B)/2 [ sin^2(A+B)/2 + cos^2(A+B)/2 ]
= 4 sin^2(A- B)/2 *1
= R.H.S.

Que-24: (i) cos²(π/8) + cos²(3π/8) + cos²(5π/8) + cos²(7π/8) = 2.
(ii) sin^4(π/8) + sin^4(3π/8) + sin^4(5π/8) + sin^4(7π/8) = 3/2

Sol: (i) LHS = cos²(⁡π/8) + cos²(⁡3π/8) + cos²(⁡5π/8) + cos²(⁡7π/8)
= cos²(⁡π/8) + cos²(⁡3π/8) + cos²⁡(π−(3π/8)) + cos²⁡(π−(π/8))
= cos²(⁡π/8) + cos²(⁡3π/8) + {−cos⁡(3π/8)}² + {−cos⁡(π/8)}²
= cos²(⁡π/8) + cos²(⁡3π/8) + cos²(⁡3/π8) + cos²(⁡π/8)
= 2(cos²⁡(π/8) + cos²(⁡3π/8))
= 2{cos²(⁡π/8) + cos²⁡((π/2)−(π/8))}
= 2(cos²(⁡π/8) + sin²(π/8))
= 2 = RHS
Hence proved.

(ii) LHS = sin^4(π/8) + sin^4(3π/8) + sin^4(5π/8) + sin^4(7π/8)

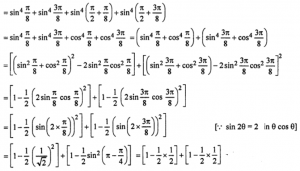
= (3/4) + (3/4)
= 3/2 = RHS.

Que-25: cos α cos (60° – α) cos (60° + α) = (1/4) cos 3α.

Sol: LHS = cosA ⋅ cos(60∘-A) ⋅ cos(60∘+A)
= (cos A) (cos 60° cos A + sin 60° sin A) . (cos 60° cos A – sin 60° sin A)
= (cosA)((1/2)cosA + (√3/2)sinA) ((1/2)cosA – (√3/2)sinA)
= (1/4) cosA (cos²A – 3sin²A)
= (1/4)[cos³A-3cosA(1-cos²A)]
= (1/4) (4cos³A – 3cosA)
= (1/4) cos A

Que-26: (cos³α−cos³α)/cosα + (sin³α+sin³α)/sinα = 3.

Sol: LHS = (cos³α−cos³α)/cosα + (sin³α+sin³α)/sinα
= {(cos³α-(4cos³α-3cosα))/cosα} + {(sin³α+(3sinα-4sin³α))/sinα}
= {-3cos³α+3cosα}/cosα + {3sinα-3sin³α}/sinα
= -3cos²α + 3 + 3 – 3sin²α
= 6 – 3(cos²α + sin²α)
= 6 – 3 × 1
= 3 = RHS.

Que-27: cos² 2θ – sin² θ = cos θ . cos 3θ.

Sol: R.H.S = cos θ cos 3θ = cos θ (4 cos³ θ – 3 cos θ) = 4 cos⁴ θ – 3 cos² θ
L.H.S = cos² 2θ – sin² θ = (2 cos² θ – 1)² – (1 – cos² θ)
= 4 cos⁴ θ – 4 cos² θ + 1 – 1 + cos² θ
= 4 cos⁴ θ – 3 cos² θ
∴ L.H.S = R.H.S

Que-28: 1 + {(cos2θ+cos6θ)/cos4θ} = sin3θ/sinθ.

Sol: LHS = 1 + {(cos2θ+cos6θ)/cos4θ}

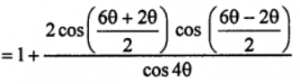
= 1 + {(2cos4θcos2θ)/cos4θ}
= 1 + 2cos 2θ = 1 + 2(1-2sin²θ)
= 3 – 4sin²θ
= {sinθ(3-4sin²θ)/sinθ}
= (3sinθ-4sin³θ)/sinθ
= sin3θ/sinθ = RHS.

Que-29: cos³(x−(2π/3)) + cos³x + cos³(x+(2π/3)) = (3/4)cos3x

Sol: LHS = cos³(x−(2π/3)) + cos³x + cos³(x+(2π/3))
cos³(x + 2π/3) + cos³(x + 4π/3) = -{cos³(π/3 + x) + cos³(π/3 – x)}
Applying the identity, a³ + b³ = (a + b)³ – 3ab(a + b),
-{cos³(π/3 + x) + cos³(π/3 – x)} =
= -[{cos(π/3 + x) + cos(π/3 – x)}³ -3cos(π/3 + x)*cos(π/3 – x){cos(π/3 + x) + cos(π/3 – x)}]
= -[{2cos(π/3)*cos(x)}³ – 3{cos²x – sin²(π/3)}{2cos(π/3)*cos(x)}]
= -[cos³x – 3(cos²x – 3/4)*cos(x)] = -[cos³x – 3cos³x + (9/4)*cos(x)]
= 2cos³x – (9/4)*cos(x)
So of the above left side = cos³x + 2cos³x – (9/4)*cos(x) = 3cos³x – (9/4)*cos(x)
= (3/4){4cos³x – 3*cos(x)} [Identity: 4cos³x – 3*cos(x) = cos(3x)]
= (3/4)*cos(3x) = RHS.
Hence, Proved

Que-30: (1/sin10°) − (√3/cos10°) = 4.

Sol: LHS = 1/sin10-√3/cos10
= (cos10 – √3sin10)/cos10sin10
multiplying 1/2 in denominator and numerator
= {(cos10/2) – (√3sin10/2)}/(cos10sin10/2)
= (cos60cos10 – sin60sin10)/(cos10sin10/2)
= cos(60 + 10)/(cos10sin10/2)
= cos70/(cos10sin10/2)
= 2cos70/cos10sin10
multiplying 2 on numerator and denominator
= 4cos70/2sin10cos10
= 4cos70/sin20
= 4cos70/cos70
= 4  proved

Que-31: tan 70° – tan 20° – 2 tan 40° = 4 tan 10°.

Sol: LHS = tan 70° – tan 20° – 2 tan 40°
= tan (90°-20°) – tan 20° – 2 tan 40°
=  cot 20° – tan 20° – 2 tan 40°
= (1/tan 20°) – tan 20° – 2 tan 40°
= {(1-tan²20°)/tan 20°} – 2 tan 40°
= 2{(1-tan²20°)/2tan 20°} – 2 tan 40°
= 2cot 20° – 2tan 40°
= 2{(1/tan 40°) – tan 40°}
= 2×2 {(1-tan²40°)/2tan 40°}
= 4cot (2×40°)
= 4cot (90°-10°)
= 4 tan 10°

Que-32: tan θ + 2 tan 2θ + 4 tan 4θ + 8 cot 8θ = cot θ.

Sol: We know that cot θ – tan θ = 2 cot 2θ … (1)
L.H.S = tan θ + 2 tan 2θ + 4 tan 4θ + 8 cot 8θ
= cot θ – (cot θ – tan θ) + 2 tan 2θ + 4 tan 4θ + 8 cot 8θ
= cot θ – 2 cot 2θ + 2 tan 2θ + 4 tan 4θ + 8 cot 8θ [using (1)]
= cot θ – 2 [cot 2θ – tan 2θ] + 4 tan 4θ + 8 cot 8θ
= cot θ – 2 x 2 cot 4θ + 4 tan 4θ + 8 cot 8θ = cot θ – 4 [cot 4θ – tan 4θ] + 8 cot 8θ
= cot θ – 8 cot 8θ + 8 cot 8θ = cot θ = R.H.S

Que-33: (i) 4 (cos³ 20° + cos³ 40°) = 3 (cos 20° + cos 40°).
(ii) 4 (cos³ 10° + sin³ 20°) = 3 (cos 10° + sin 20°).

Sol: (i) We know that cos 3θ = 4 cos³ θ – 3 cos θ
L.H.S = 4 (cos³ 20° + cos³ 40°)
= [cos (3 x 20°) + 3 cos 20°] + [cos (3 x 40°) + 3 cos 40°]
= [cos 60° + 3 cos 20°] + [cos 120° + 3 cos 40°]
= (1/2) + 3 cos 20° + cos (180° – 60°) + 3 cos 40°
= (1/2) + 3 cos 20° – (1/2) + 3 cos 40°
= 3 (cos 20° + cos 40°) = R.H.S

(ii) L.H.S. = 4 cos³ 10° + 4 sin³ 20°
= [cos (3 x 10°) + 3 cos 10°] + [3 sin 20° – sin 60°] [∵ cos 3θ = 4 cos³ θ – 3 cos θ ; sin 3θ = 3 sin θ – 4 sin³ θ]
= (√3/2) + 3 cos 10° + 3 sin 20° – (√3/2)
= 3 (cos 10° + sin 20°) = R.H.S

Que-34: cos³ x sin² x = (1/16) (2 cos x – cos 3x – cos 5x).

Sol: LHS = cos³ x sin² x
= cos³(x) * (1 – cos²(x))
= cos³(x) * (1 – cos²(x)) = (cos²(x)) * cos(x) * (1 – cos²(x))
= cos(x) * (cos²(x)) * (1 – cos²(x))
= cos(x) * (1 – sin²(x)) * (1 – cos²(x))
= cos(x) * cos²(x) * (1 – cos²(x))
= cos(x) * (cos²(x) – cos⁴(x))
Now, let’s focus on the RHS:
(1/16) (2cos(x) – cos(3x) – cos(5x))
= (1/16) (2cos(x) – (4cos³(x) – 3cos(x)) – (16cos⁵(x) – 20cos³(x) + 5cos(x)))
= 32cos(x) – (64cos⁴(x) – 48cos²(x) + 12cos(x)) – (16cos⁵(x) – 20cos³(x) + 5cos(x))
= 32cos(x) – 64cos⁴(x) + 48cos²(x) – 12cos(x) – 16cos⁵(x) + 20cos³(x) – 5cos(x)
= -16cos⁵(x) + 64cos⁴(x) + 20cos³(x) + 48cos²(x) + 32cos(x) – 12cos(x) – 5cos(x)
= 4cos(x)(-4cos⁴(x) + 16cos³(x) + 5cos²(x) + 12cos(x) – 3)
= -4cos⁴(x) + 16cos³(x) + 5cos²(x) + 12cos(x) – 3 = cos(x) * (cos²(x) – cos⁴(x))
So, the LHS and RHS are equal:
cos³(x) * sin²(x) = 16(2cos(x) – cos(3x) – cos(5x))

Que-35: cot A + cot (60° + A) + cot (120° + A) = 3 cot 3A.

Sol: LHS = cot A + cot (60° + A) + cot (120° + A)
= cot A + cot (60° + A) + cot (180° – 60° + A)
= cot A + cot (60° + A) + cot (60° – A)

= {3(1-3tan²A)}/{3tanA-tan³A}
= 3cot 3A = RHS.

Que-36: (i) cos 36° – sin 18° = (1/2).
(ii) cos² 36° + sin² 18° = (3/4).
(iii) 3 cos 72° – 4 sin³ 18° = cos 36°.
(iv) cos² 48° – sin² 12° = (√5+1)/8.
(v) sin (1/10)π cos (1/5)π = (1/4).
(vi) sec 72° – sec 36° = 2.
(vii) sin² 24° – sin² 6° = (√5−1)/8.
(viii) sin² (π/5) sin² (2π/5) = 5/16.

Sol: (i) L.H.S = cos 36° – sin 18°
= (√5+1)/4 − (√5−1)/4
= (√5+1−√5+1)/4
= 1/2 = R.H.S

(ii) L.H.S. = cos² 36° + sin² 18°
= ((√5+1)/4)² + ((√5−1)/4)²
= (1/16) [5+1+2√5+5+1−2√5]
= 12/16 = 3/4

(iii) L.H.S = 3 cos 72° – 4 sin3 18°
= 3 cos (90° – 18°) – 4 sin3 18° = 3 sin 18° – 4 sin3 18°
= sin (3 x 18°) [∵ 3 sin θ – 4 sin³ θ = sin 3θ]
= sin 54° = sin (90° – 36°) = cos 36° = R.H.S

(iv) L.H.S = cos2 48° – sin2 12° = cos (48° + 12°) cos (48° – 12°) [∵ cos (A + B) cos (A – B) = cos² A – sin² B]
= cos 60° cos 36°
= (1/2) × {(√5+1)/4}
= (√5+1)/8 = R.H.S

(v) LHS = sin (1/10)π cos (1/5)π
= sin 18° cos 36°
= {(√5-1)/4} {(√5+1)/4}
= (5-1)/16
= 1/4 = RHS.

(vi) LHS = sec 72° – sec 36°
= (1/cos 72°) – (1/cos 36°)
= {1/cos (90°-18°)} – (1/cos 36°)
= (1/sin 18°) – (1/cos 36°)
= {4/(√5-1)} – {4/(√5+1)}
= [4{√5+1-√5+1}]/(√5²-1²)
= 8/5-1
= 2 = RHS.

(vii) LHS = sin² 24° – sin² 6°
= sin (24°+6°) sin (24°-6°)
= sin 30° sin 18°
= (1/2) {(√5-1)/4}
= (√5-1)/8

(viii) LHS = sin² (π/5) sin² (2π/5)
= (sin 36° sin 72°)²
= (sin 36° sin (90°-18°))²
= (sin 36° cos 18°)²

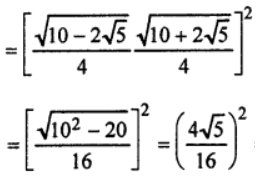
= 5/16 = RHS.

Que-37: (i) sin 12° sin 48° sin 54° = (1/8).
(ii) 4 cos 6° cos 42° cos 66° cos 78° = (1/4).
(iii) sin (π/5) sin (2π/5) sin (4π/5) sin (3π/5) = 5/16
(iv) cos (2π/15) cos (4π/15) cos (8π/15) cos (16π/15) = 1/16
(v) cos² (π/10) + cos² (2π/5) + cos² (3π/5) + cos² (9π/10) = 2
(vi) tan 6° tan 42° tan 66° tan 78° = 1

Sol: (i) LHS = sin 12° sin 48° sin 54°
= (1/2) [2sin 48° sin 12°] sin 54°
= (1/2) [cos (48°-12°) – cos (48°+12°)] sin 54°
= (1/2) [cos 36° – cos 60°] sin 54°
= (1/2) [cos 36° – (1/2)] sin 54°

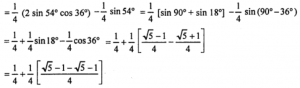
= (1/4) – (1/8)
= 1/8 = RHS.

(ii) LHS = 4 cos 6° cos 42° cos 66° cos 78°
= (2cos 66° cos 6°) (2cos 78° cos 42°)
= (cos 72° + cos 60°) (cos 120° + cos 36°)

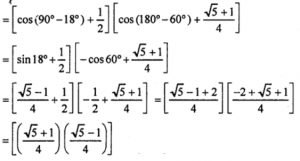
= (5-1)/16
= 1/4 = RHS

(iii) If A + B = π, then
⇒ A = π – B ⇒ sin A = sin(π-B) = sin A = sin B
∴ π/5 + 4π/5 = π ⇒ sin π/5 = sin 4π/5 and 2π/5 + 3π/5 = π ⇒ sin 2π/5 = sin 3π/5
∴ L.H.S. = sin π/5 sin 2π/5 sin 3π/5 sin 4π/5
= L.H.S. = sin π/5 sin 2π/5 sin 2π/5 sin π/5
⇒ L.H.S. = (sin π/5 sin 2π/5)² = (sin 36° sin 72°)² = (sin 36° sin 18°)²
⇒ L.H.S.= {(√10-2√5/4) × (√10+2√5/4)}² = (10-2√5/16) × 10+2√5/16
⇒ L.H.S = 100-20/256 = 80/256 = 5/16 = R.H.S.
L.H.S. = R.H.S. hence proved.

(iv) Let L.H.S be cos 2π/15. cos 4π/15. cos 8π/15. cos 16π/15
cos 2π/15=cos (2×180)/15=cos(360/15)=cos24°
Similarly : cos 4π/15.=Cos48°
cos 8π/15=cos 96°
cos 16π/15=Cos 192°
∴L.H.S = cos24° Cos48° cos 96° Cos 192°
Multiply and Divide the equation by 16 sin24°
⇒ (1/16 sin24°)[(2sin24°cos24°)(2Cos48°)(2cos 96°)(2 Cos 192°)]
⇒ (1/16 sin24°)[Sin48°(2Cos48°)(2cos 96°)(2 Cos 192°)] [∵Sin2A=2sinACosA]
⇒ (1/16 sin24°)[(2Sin48°Cos48)(2cos 96°)(2 Cos 192°)]
⇒ (1/16 sin24°)([2sin96°cos96°)((2 Cos 192°)]
⇒ (1/16 sin24°)([2sin192°Cos 192°)]
⇒ (1/16 sin24°)[sin384°]
⇒ sin384°/16 Sin 24°
⇒ Sin(360+24)/16sin24°
⇒ Sin24°/16 sin24°
⇒ 1/16
L.H.S = R.H.S
Hence proved

(v) cos² (π/10) + cos² (2π/5) + cos² (3π/5) + cos² (9π/10) = 2
cos²180°/16 + cos²540°/16 + cos²900°/16 + cos²1260°/16
= cos²π/16 + cos²3π/16 + cos²5π/16 + cos²7π/16 [180°/16 = π/16 (say)]
= cos²π/16 + cos²3π/16 + cos²(π/2-3π/16) + cos²(π/2-π/16)
= cos²π/16 + cos²3π/16 + sin²3π/16 + sin²π/16 [∵. cos(π/2-Ф) = sinФ]
= (sin²π/16+cos²π/16) + (sin²3π/16+cos²3π/16)
= 1+1 [∵, sin²Ф+cos²Ф = 1]
= 2

(vi) tan 6° tan 42° tan 66° tan 78° = 1
L.H.S. = tan6° tan42° tan66° tan78°
= (sin6°/cos6°) ⋅ (sin42°/cos42°) ⋅ (sin66°/cos66°) ⋅ (sin78°/cos78°)
= [(2sin66°sin6°)(2sin78°sin42°)]/[(2cos66°cos6°)(2cos78°cos42°)
= [{cos(66°-6°)-cos(66°+6°)}/{cos(66°+6°)+cos(66°-6°)}] ⋅ [{cos(78°-42°)-cos(78°+42°)}/{cos(78°+42°)+cos(78°-42°)}]
= [(cos60°- cos72°)(cos36°- cos120°)]/[(cos60°+ cos72°)(cos36°+ cos120°)]
= [(cos60°- sin18°)(cos36°+ sin30°)]/[(cos60°+ sin18°)(cos36°- sin30°)]  …[∵ cos(90° + θ) = – sin θ]
= [[(1/2) – {√5-1}/4] [{(√5+1)/4} + (1/2)]] / [(1/2) + {(√5-1)/4}] [{(√5+1)/4} – (1/2))]]
= (9-5)/(5-1)
= 1
= R.H.S.

Que-38: cos α cos 2α cos 4α cos 8α = (1/16), if a = 24°.

Sol: LHS = cos α cos 2α cos 4α cos 8α
= (1/2sin α) (2sin α cos α) cos 2α cos 4α cos 8α
= (1/2² sin α) (2 sin 2α cos 2α) cos 4α cos 8α
= (1/2×2² sin α) (2sin 4α cos 4α) cos 8α

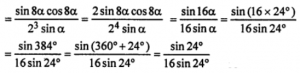
= 1/16 = RHS.

Que-39: cos 12° cos 24° cos 36° cos 48° cos 72° cos 84° = 1/2^6

Sol: LHS = cos 12° cos 24° cos 36° cos 48° cos 72° cos 84°
= cos α cos 2α cos3α cos 4α cos 6α cos 7α
where α = 12° and 15α = 180°   ……. (1)

Que-40: If θ = {π/(2^n)+1}  prove that 2ⁿ cos θ cos 2θ cos 2² θ ………. cos 2^n-1 θ = 1.

Sol: LHS = 2ⁿ cos θ cos 2θ cos 2² θ ………. cos 2^n-1 θ

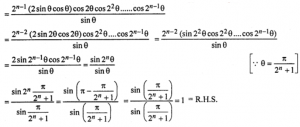
Que-41: If tan {(x-y)/2}, tan z, tan {(x+y)/2} are in GP., then show that cos x = cos.y. cos 2z.

Sol: Since, tan {(x-y)/2}, tan z, tan {(x+y)/2} are in GP.,
tan² z = tan {(x-y)/2} tan {(x+y)/2}

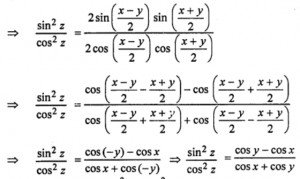
= (cos x + cos y) sin²z = cos²z (cos y – cos x)
= cos x (sin²z+cos²z) = cos y (cos²z-sin²z)
= cos x = cos y . cos 2z

Que-42: If sin θ is GM. of sin Φ and cos Φ, then prove that cos 2θ = 2 cos²(π/4 + Φ)

Sol: Given sin θ is GM. of sin Φ and cos Φ
= sin²θ = sin Φ cos Φ
= {(1-cos 2θ)/2} = sin Φ cos Φ
= 1-cos 2θ = sin 2Φ = -cos {(π/2) + 2Φ}
= cos 2θ = 1 + cos {(π/2) + 2Φ}
= cos 2θ = 2cos² {(π/4) + Φ}

Que-43: If m tan (θ – 30°) = n tan (θ + 120°), show that cos 2θ = (m+n)/{2(m+n)}

Sol: Given m tan (θ – 30°) = n tan (θ + 120°)
m/n = (θ + 120°)/(θ – 30°) ;  Applying componendo and dividendo, we get
(m+n)/(m-n) = {tan (θ + 120°) + tan (θ – 30°)}/{tan (θ + 120°) – tan (θ – 30°)}
= [{sin(θ + 120°)/cos(θ + 120°)} + {sin(θ – 30°)/cos(θ – 30°)}] / [{sin(θ + 120°)/cos(θ + 120°)} – {sin(θ – 30°)/cos(θ – 30°)}]
= [sin(θ + 120°)cos(θ – 30°) + sin(θ – 30°)cos(θ + 120°)] / [sin(θ + 120°)cos(θ – 30°) – sin(θ – 30°)cos(θ + 120°)]
= [sin (θ + 120° + θ – 30°)] / [sin (θ + 120° – θ + 30°)]
= [sin (2θ + 90°)]/sin 150°
= sin 2θ/sin (180°-30°)
= 2 cos 2θ = (m+n)/{2(m+n)}

Que-44: If sin α = λ sin (θ – α) then prove that tan {α – (θ/2)} = (λ-1)/(λ+1) tan θ/2

Sol: Given sin α = λ sin (θ – α)
= sin α/sin (θ – α) = λ /1
= Applying Componendo and Dividendo we have,

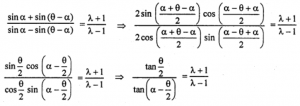
= tan {α – (θ/2)} = (λ-1)/(λ+1) tan (θ/2)

Que-45: If tan (α/2) = √{(1-e)/(1+e)} tan (β/2), Prove that cos ß = (cos α – e)/(1 – e cos α)

Sol: Given : tan (α/2) = √{(1-e)/(1+e)} tan (β/2)
On squaring, we have,
tan² (α/2) = {(1-e)/(1+e)} tan² (β/2)
= [1/tan² (β/2)] = {(1-e)/(1+e)} [1/tan² (α/2)]
Applying Componendo and Dividendo; we have,

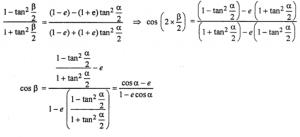
Que-46: If sin θ = n sin (θ+2α), show that (n-1) tan (θ+α)+(n+1)tan α = 0.

Sol: sin θ = n sin (θ+2α)
sin θ/sin (θ+2α) = n
Using Componendo and Dividendo, we have,
{sin θ+sin (θ+2α)}/{sin θ-sin (θ+2α)} = (n+1)/(n-1)
= [2sin{(2θ+2α)/2} cos (-2α/2)] / [{2sin (-2α/2)} cos{(2θ+2α)/2}] = (n+1)/(n-1)
= [cos (θ+α) cos α] / [-sin α cos (θ+α)] = (n+1)/(n-1)
= tan (θ+α) -cot α = (n+1)/(n-1)
= (n-1) tan (θ+α) = (n+1) / -cot α
= (n-1) tan (θ+α) = – (n+1) tan α
= (n-1) tan (θ+α) + (n+1) tan α = 0.

Que-47: If cos2α = {3cos 2β-1}/{3-cos 2β}, then prove that tanα = √2 tanβ

Sol: Given :
cos⁡2α = (3cos ⁡2β − 1)/(3 − cos ⁡2β)
Using componendo and dividendo
⇒ (cos ⁡2α−1)/(cos ⁡2α+1) = [(3cos ⁡2β−1) − (3−cos⁡ 2β)] / [(3cos ⁡2β−1) + (3−cos⁡ 2β)]
⇒ (cos⁡ 2α−1)/(cos⁡ 2α+1) = (4cos ⁡2β−4)/(2cos ⁡2β+2)
⇒ −(1−cos ⁡2α)/(1+cos⁡ 2α) = [−4(1−cos ⁡2β)]/[2(1+cos ⁡2β)]
⇒ (1−cos ⁡2α)/(1+cos ⁡2α) = [2(1−cos⁡ 2β)]/[(1+cos ⁡2β)]
⇒ (2sin²α)/(2cos²⁡α) = [2(2sin²⁡⁡β)]/(2cos²⁡⁡β)
⇒ tan 2⁡α = 2tan 2⁡β
∴ tan⁡α = 2tan ⁡β

Que-48: Prove that [{cosA+cosB}/{sinA-sinB}]^n + [{sinA+sinB}/{cosA-cosB}]^n = 2cot^n {(A-B)/2}, if n is even   0, if n is odd

Sol:  we can rewrite the LHS:
(cosA+cosB)/(sinA−sinB) = [2cos{(A+B)/2}cos{(A−B)/2}] / [2cos{(A+B)/2}sin{(A−B)/2}
= [cos{(A−B)/2}]/[sin{(A−B)/2}] = cot(A−B)/2
Similarly, for the second term:
(sinA+sinB)/(cosA−cosB) = [2sin{(A+B)/2}cos{(A−B)/2}] / [−2sin{(A+B)/2}sin{(A−B)/2}]
= − [cos{(A−B)/2}] / [sin{(A−B)/2}]
= −cot (A−B)/2
Now substituting these results back into the LHS:
[cot{(A−B)/2}]^n + [−cot{(A−B)/2}]^n
If n is even:
[cot{(A−B)/2}]^n + [−cot{(A−B)/2}]^n = 2cot^n (A−B)/2
If n is odd:
[cot{(A−B)/2}]^n + [−cot{(A−B)/2}]^n = 0

Que-49: Prove that [2/√[2+]√{2+}√(2+2cos 4x)] = sec x/2

Sol:  LHS = [2/√[2+]√{2+}√(2+2cos 4x)]
= [2/√[2+]√{2(1+cos 4x)]
= [2/√[2+]√{2×2 cos²2x]
= 2/√{2 + 2cos ⁡2x}
= 2/√{2(1+cos⁡ 2x)}
= 2/√{2.2cos²⁡x}   (∵ 2cos²x = 1+cos⁡2x)
= 2/2 cos x
= cos x = sec x/2
Hence proved .

Que-50: If tan x, tan y, tan z are in G.P., show that cos 2y = {cos (x+z)}/{cos (x-z)}

Sol: Since tan x, tan y, tan z are in G.P., we can express this condition mathematically:
tan²y = tan x ⋅ tan z
We can also write this in terms of the reciprocal:
1/tan²y  = 1/(tan x ⋅ tan z)
cos²y/sin²y = (cos x ⋅ cos z)/(sin x ⋅ sin z)
Cross-multiplying gives:
cos²y ⋅ sin x ⋅ sin z = cos x ⋅ cos z ⋅ sin²y
Substitute tan²y = (sin²y)/cos²y) :
cos2y = [1−{(sin²y)/(cos²y)}] / [1+{(sin²y)/(cos²y)}]
= (cos²y−sin²y)/(cos²y+sin²y)
We can express cos²y−sin²y and cos²y+sin²y in terms of cos(x+z) and cos(x−z) :
cos²y − sin²y = cos x cos z − sin x sin z = cos (x+z)
cos²y + sin²y = cos x cos z + sin x sin z = cos (x−z)
Therefore, we have:
cos2y = {cos(x+z)}/{cos(x−z)}

Que-51: If tan α/2 : tan β/2 = 1 : √3, show that cos β = {2cos α -1}/{2-cos α}

Sol:  Given : tan α/2 : tan β/2 = 1 : √3
{tan α/2}/{tan β/2} = {1/√3}
tan α/2 = {1/√3} {tan β/2}
tan α/2 = √[(1-cos α)/(1+cos α)]
tan β/2 = √[(1-cos β)/(1+cos β)]
Substitute into the ratio :
√[(1-cos α)/(1+cos α)] = {1/√3} √[(1-cos β)/(1+cos β)]
[(1-cos α)/(1+cos α)] = {1/3} [(1-cos β)/(1+cos β)]
Multiply both sides by 3
3 [(1-cos α)/(1+cos α)] = [(1-cos β)/(1+cos β)]
Let x = cos α
[(1-cos β)/(1+cos β)] = 3 [(1-x)/(1+x)]
[(1-cos β)/(1+cos β)] =  [3(1-x)/(1+x)]
(1-cos β) (1+x) = (1+cos β) {3(1-x)}
(1-cos β) (1+x) = 1 + x – cos β – x cos β
= 1 + x – cos β (1+x)
(1+cos β) {3(1-x)} = 3 {1 – x + cos β – x cos β}
= 3 {1 – x + cos β (1-x)}
= 3 [(1-x)(1+ cos β)]
1 + x – cos β (1+x) = 3 [(1-x)(1+ cos β)]
1 + x – cos β (1+x) – 3 [(1-x)(1+ cos β)] = 0
LHS = 1 + x – cos β – x cos β = (1+x) – cos β (1+x)
RHS = 3 {1 + cos β – x – x cos β} = 3 {1 – x + cos β – x cos β}
After simplification you get :
cos β = {2cos α -1}/{2-cos α}

–: End Compound and Multiple Angles Class 11 OP Malhotra Exe-5D ISC Math Ch-5 Solution :–

Return to :- OP Malhotra ISC Class-11 S Chand Publication Maths Solutions

Thanks

Please share with your friends