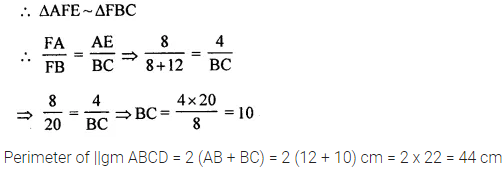Concise Solutions Chapter-15 Similarity ICSE Maths Class 10. Solutions of Exercise – 15 (A), Exercise – 15 (B), Exercise – 15 (C), Exercise – 15 (D) and Exercise – 15 (E), for Concise Selina Maths of ICSE Board Class 10th. Concise Solutions Chapter-15 Similarity for ICSE Maths Class 10 is available here. All Solutions of Concise Selina of Chapter-15 Similarity has been solved according instruction given by council. This is the Solutions of Chapter-15 Similarity for ICSE Class 10th. ICSE Maths text book of Concise is In series of famous ICSE writer in maths publications. Concise is most famous among students.
Concise Solutions Chapter-15 Similarity ICSE Maths Class 10
The Solutions of Concise Mathematics Chapter-15 Similarity for ICSE Class 10 have been solved. Experience teachers Solved Chapter-15 Similarity to help students of class 10th ICSE board. Therefore the ICSE Class 10th Maths Solutions of Concise Selina Publishers helpful on various topics which are prescribed in most ICSE Maths textbook
–:Select Topic :–
Exercise – 15 (A), Exercise-15(B), Exercise – 15 (C) , Exercise – 15 (D) , Exercise – 15 (E)
How to Solve Concise Maths Selina Publications Chapter-15 Similarity
Note:- Before viewing Solutions of Chapter-15 Similarity of Concise Selina Maths read the Chapter Carefully then solve all example of your text book. The Chapter-15 Similarity is main Chapter in ICSE board
EXERCISE – 15 (A), Selina Concise Maths Solutions of Chapter-15 Similarity Map and Models
Question 1.
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that:
(i) ΔAPC and ΔBPD are similar.
(ii) If BD = 2.4 cm AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm; find the lengths of PA and PC.
Answer 1
Two line segments AB and CD intersect each other at P.
AC || BD To prove:
(i) ΔAPC ~ ΔBPD
(ii) If BD = 2.4cm, AC = 3.6cm, PD = 4.0 cm and PB = 3.2, find length of PA and PC
Proof:
(i) In ΔAPC and ΔAPD
∠APC = ∠BPD (Vertically opp. angles)
∠PAC = ∠PBD (Alternate angles)
ΔAPC ~ ΔBPD (AA axiom)

Question 2.
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that:
(i) ΔAPB is similar to ΔCPD.
(ii) PA x PD = PB x PC.
So
Answer 2
In trapezium ABCD AB || DC
Diagonals AC and BD intersect each other at P.
To prove:
(i) ΔAPB ~ ΔCPD.
(ii) PA x PD= PB x PC.
Proof: In ΔAPB and ΔCPD
∠APB = ∠CPD (Vertically opposite angles)
∠PAB = ∠PCD (Alternate angles)
ΔAPB ~ ΔCPD (AA axiom)
=
=> PA x PD = PB x PC
Hence proved.
Question 3.
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that:
(i) DP : PL = DC : BL.
(ii) DL : DP = AL : DC.
Answer 3
P is a point on side BC of a parallelogram ABCD.
DP is produced to meet AB produced at L.
To prove:
(i) DP : PL = DC : BL
(ii) DL : DP = AL : DC.
Proof:
(i) In ΔBPL and ΔCPD
∠BPL = ∠CPD (Vertically opposite angles)
∠PBL = ∠PCD (Alternate angles)
ΔBPL ~ ΔCPD (AA axiom)

Question 4.
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that:
(i) ΔAOB is similar to ΔCOD.
(ii) OA x OD = OB x OC.
Answer 4
Given : In quadrilateral ABCD, diagonals AC and BD intersect each other at O.
AO = 2CO, BO = 2DO.
To prove:
(i) ΔAOB is similar to ΔCOD.
(ii) OA x OD = OB x OC.

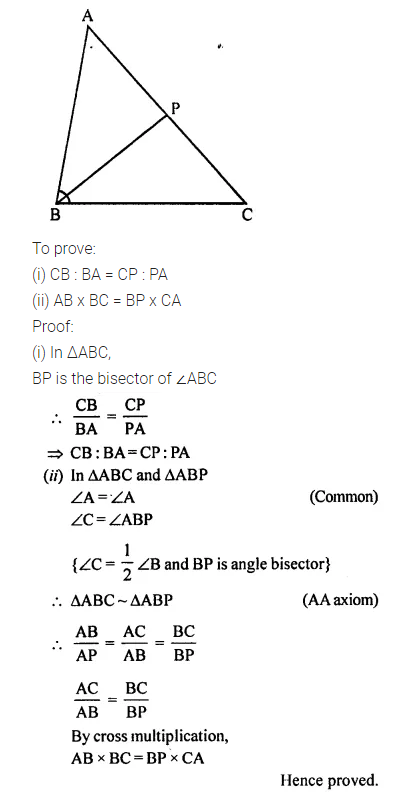
Question 5.
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that:
(i) CB : BA = CP : PA
(ii) AB x BC = BP x CA
Answer 5
In ΔABC,
∠ABC = 2∠ACB
Bisector of ∠ABC meets AC in P.
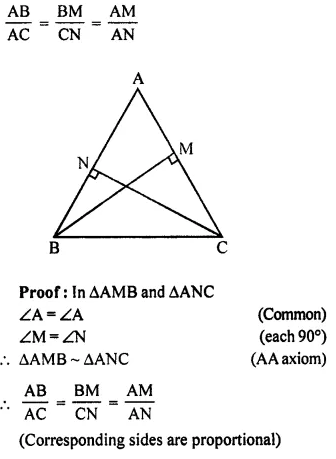
Question 6.
In ΔABC; BM ⊥ AC and CN ⊥ AB; show that:
……………………
Answer 6
In ΔABC,
BM ⊥ AC and CN ⊥ AB
To prove:
Question 7.
In the given figure, DE // BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.
(i) Write all possible pairs of similar triangles.
(ii) Find lengths of ME and DM.
Answer 7
In the given figure,
DE || BC
AE = 15 cm, EC = 9 cm NC = 6 cm and BN = 24 cm
(i) Write all the possible pairs of similar triangles.
(ii) Find lengths of ME and DM
Proof:
(i) In ΔABC
DE || BC
Pairs of similar triangles are
(a) ΔADE ~ ΔABC
(b) ΔADM ~ ΔABN
(c) ΔAME ~ ΔANC
(ii) ΔAME ~ ΔANC
and ΔADM ~ ΔABN


Question 8.
In the given figure, AD = AE and AD² = BD x EC
Prove that: triangles ABD and CAE are similar.
Answer 8
In the given figure,
AD = AE
AD² = BD x EC
To prove: ΔABD ~ ΔCAE
Proof: In ΔADC, AD = AE
∠ADE = ∠AED (Angles opposite to equal sides)
But ∠ADE + ∠ADB = ∠AED + ∠AEC = 180°
∠ADB = ∠AEC
AD² = BD x EC

Question 9.
In the given figure, AB // DC, BO = 6 cm and DQ = 8 cm; find: BP x DO.
Answer 9
In the given figure, AB || DC,
BO = 6 cm, DQ = 8 cm
Find BP x DO
In ΔODQ and ΔOPB
∠DOQ = ∠POB (Vertically opposite angles)
∠DQO = ∠OPB (Alternate angles)

Question 10.
Angle BAC of triangle ABC is obtuse and AB = AC. P is a point in BC such that PC = 12 cm. PQ and PR are perpendiculars to sides AB and AC respectively. If PQ = 15 cm and PR = 9 cm; find the length of PB.
Answer 10
In ΔABC, ∠ABC is an obtused angle,
AB =AC
P is a point on BC such that PC = 12 cm
PQ and PR are perpendiculars to the sides AB and AC respectively.
PQ = 15 cm and PR = 9 cm

Question 11
State, true or false :
(i) Two similar polygons are necessarily congruent
(ii) Two congruent polygons are necessarily similar.
(iii) All equiangular triangles are similar.
(iv) All isosceles triangles are similar.
(v) Two isosceles-right triangles are similar.
(vi) Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
(vii) The diagonals of a trapezium, divide each other into proportional segments.
Answer 11
(i) False,
(ii) True,
(iii) True,
(iv) False,
(v) True,
(vi) True,
(vii) True.
Question 12.
Given………………..4x+2
find……………………..DE
Answer 12

Question 13.
D is a point on the side BC of triangle ABC such that angle ADC is equal to angle BAC. Prove that CA² = CB x CD.
Answer 13
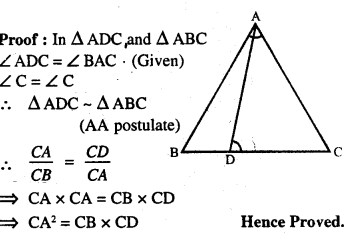
Question 14.
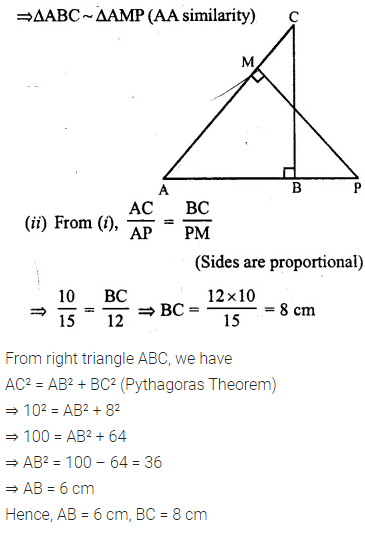
In the given figure, ΔABC and ΔAMP are right angled at B and M respectively.
Given AC = 10 cm, AP = 15 cm and PM = 12 cm.
(i) Prove ΔABC ~ ΔAMP
(ii) Find AB and BC.
Answer 14
(i) In ΔABC and ΔAMP,
∠A = ∠A (Common)
∠ABC = ∠AMP (Each = 90°)
Question 15.
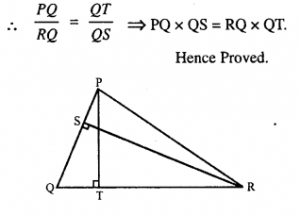
Given : RS and PT are altitudes of ΔPQR prove that:
(i) ΔPQT ~ ΔQRS,
(ii) PQ x QS = RQ x QT.
Answer 15
Proof: In ΔPQT and ΔQRS,
∠PTQ = ∠RSQ (Each = 90°)
∠Q = ∠Q (Common)
ΔPQT ~ ΔQRS (AA postulate)
Question 16.
Given : ABCD is a rhombus, DPR and CBR are straight lines.
Answer 16
on:
Proof: In ΔAPD and ΔPRC
∠DPA = ∠CPR (Vertically opposite angles)
∠PAD = ∠PCR (Alternate angles)
ΔAPD ~ ΔPRC (AA Postulate)

=Question 17.
Given: FB = FD, AE ⊥ FD and FC ⊥ AD.
Prove : =
Answer 17
 Question 18.
Question 18.
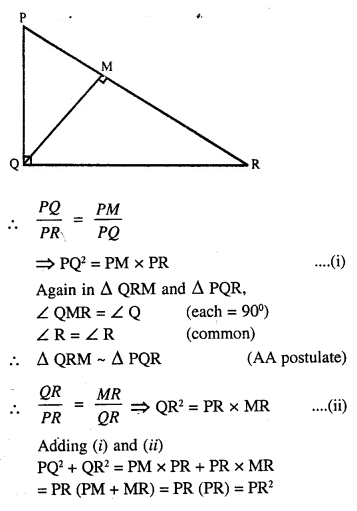
In ΔPQR, ∠Q = 90° and QM is perpendicular to PR, Prove that:
(i) PQ² = PM x PR
(ii) QR² = PR x MR
(iii) PQ² + QR² = PR²
Answer 18
Given: In ΔPQR, ∠Q =90°
QM ⊥ PR.
To Prove:
(i) PQ2 = PM x PR
(ii) QR2 = PR x MR
(iii) PQ2 + QR2 = PR2
Proof: In ΔPQM and ΔPQR,
∠QMP = ∠PQR (each = 90°)
∠P = ∠P (Common)
ΔPQM ~ ΔPQR (AA postulate
Question 19.
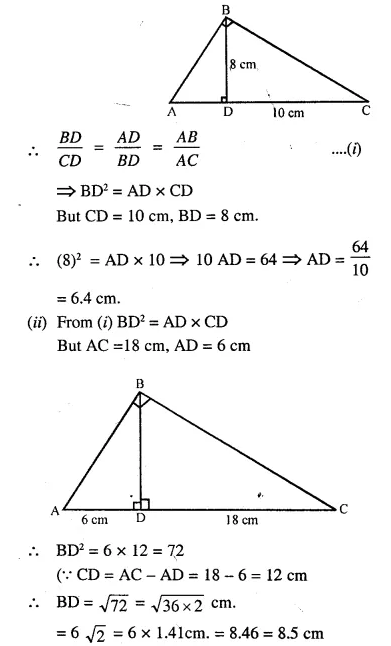
In ΔABC, ∠B = 90° and BD x AC.
(i) If CD = 10 cm and BD = 8 cm; find AD.
(ii) If AC = 18 cm and AD = 6 cm; find BD.
(iii) If AC = 9 cm, AB = 7 cm; find AD.
Answer 19
In ΔABC, ∠B = 90°
∠A + ∠C = 90° …….(i)
and in ΔBDC, ∠D = 90°
∠CBD + ∠C = 90° ….(ii)
From (i) and (ii)
∠A + ∠C = ∠CBD + ∠C
∠A = ∠CBD
Similarly ∠C = ∠ABD
Now in ΔABD and ΔCBD,
∠A = ∠CBD and ∠ABD = ∠C
ΔABD ~ ΔCBD (AA Postulate)

Question 20.
In the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm. L is a point on PR such that RL : LP = 2 : 3. QL produced meets RS at M and PS produced at N.
find……………RM
Answer 20
In ΔLNP and ΔRLQ
∠LNP = ∠LQR (Alternate angles)
∠NLP = ∠QLR (Vertically opposite angles)
ΔLNP ~ ΔRLQ (AA Postulate)

Question 21.
In quadrilateral ABCD, diagonals AC and BD intersect at point E. Such that AE : EC = BE : ED. Show that ABCD is a parallelogram.
Answer 21
Given : In quadrilateral ABCD, diagonals AC and BD intersect each other at E and

Question 22.
In ΔABC, AD is perpendicular to side BC and AD² = BD x DC. Show that angle BAC = 90°
Answer 22
Given: In ΔABC, AD x BC and AD² = BD x DC
To Prove: ∠BAC = 90°
Proof:
Question 23.
In the given figure AB || EF || DC; AB = 67.5 cm. DC = 40.5 cm and AE = 52.5 cm.
i) Name the three pairs of similar triangles.
(ii) Find the lengths of EC and EF.
Answer 23
(i) In the figure AB || EF || DC
There are three pairs of similar triangles.
(i) ΔAEB ~ ΔDEC
(ii) ΔABC ~ ΔEEC
(iii) ΔBCD ~ ΔEBF
(ii) ΔAEB ~ ΔDEC

Question 24.
In the given figure, QR is parallel to AB and DR is parallel to QB.
Prove that PQ² = PD x PA.
Answer 24
Given: In the figure QR || AB mid DR || QB.
To Prove: PQ² = PD x PA
Proof— In ΔPQB,
DR || QB (given)

Question 25.
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E.
Prove that : EL = 2 BL.
Answer 25

Question 26.
In the figure given below P is a point on AB such that AP : PB = 4 : 3. PQ is parallel to AC.
(i) Calculate the ratio PQ : AC, giving reason for your answer.
(ii) In triangle ARC, ∠ARC = 90° and in triangle PQS, ∠PSQ = 90°.
Given QS = 6 cm, calculate the length of AR. [1999]
Answer 26
Given: In ΔABC, P is a point on AB such that AP : PB = 4 : 3
and PQ || AC is drawn meeting BC in Q.
CP is joined and QS ⊥ CP and AR ⊥ CP
To Find:
(i) Calculate the ratio between PQ : AC giving reason.
(ii) In ΔARC ∠ARC= 90°
and In ΔPQS, ∠PSQ = 90°, if QS = 6 cm, calculate AR.
proof:
(i) In ΔABC, PQ || AC.
Question 27.
In the right angled triangle QPR, PM is an altitude
Given that QR = 8 cm and MQ = 3.5 cm. Calculate, the value of PR.
Given: In right angled ΔQPR, ∠P = 90° PM ⊥ QR, QR = 8 cm, MQ = 3.5 cm. Calculate PR [2000]
Answer 27
In ΔPQM and ΔQPR,
∠PMQ = ∠QPR (each = 90°)
∠Q = ∠Q (common)
ΔPQM ~ ΔQPR (AA postulate)

Question 28.
In the figure given below, the medians BD and CE of a triangle ABC meet at G.
Prove that
(i) ΔEGD ~ ΔCGB
(ii) BG = 2 GD from (i) above.
Answer 28
Given: In ΔABC, BD and CE are the medians of sides AC and AB respectively which intersect each at G.
To Prove:
(i) ΔEGD ~ ΔCGB
(ii) BG = 2 GD.
Proof: D and E are the mid points of AC and AB respectively.

Selina Concise Maths Solutions EXERCISE -15 (B) of Chapter-15 Similarity
Question 1.
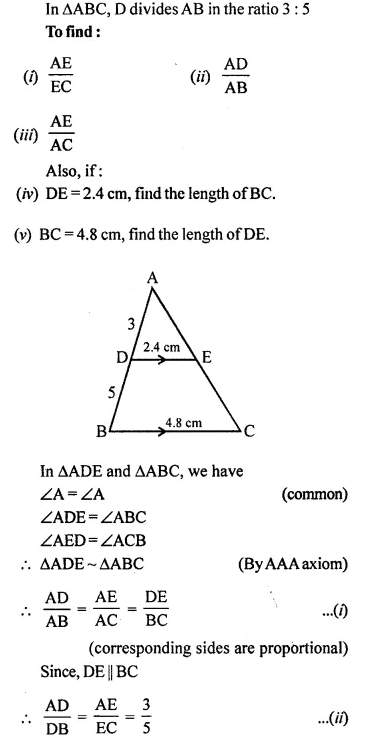
In the following figure, point D divides AB in the ratio 3 : 5. Find:
Answer 1

Question 2.
In the given figure, PQ // AB;
CQ = 4.8 cm, QB = 3.6 cm and AB = 6.3 cm. Find:
(i)
(ii) PQ
(iii) If AP = x, then the value of AC in terms of x.
Answer 2
In the given figure,
PQ || AB
CQ = 4.8 cm, QB = 3.6 cm, AB = 6.3 cm
2a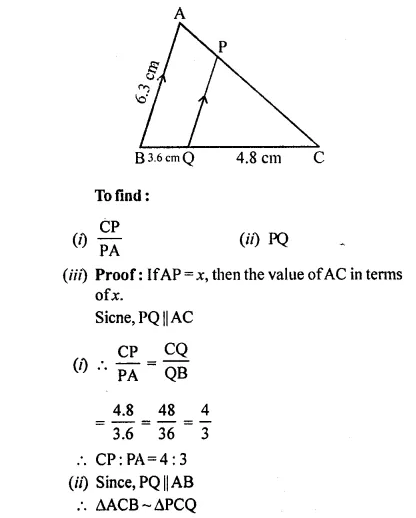

Question 3.
A line PQ is drawn parallel tp the side BC of ΔABC which cuts side AB at P and side AC at Q. If AB = 9.0 cm, CA = 6.0 cm and AQ = 4.2 cm, find the length of AP.
Answer 3
In ΔABC, PQ || BC
AB = 9.0 cm, CA = 6 cm, AQ = 4.2 cm
Question 4.
In ΔABC, D and E are the points on sides AB and AC respectively.
Find whether DE // BC, if:
(i) AB = 9 cm, AD = 4 cm, AE = 6 cm and EC = 7.5 cm
(ii) AB = 63 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
Answer 4
In ΔABC, D and E are the points on sides AB and AC respectively.
Question 5.
In the given figure, ΔABC ~ ΔADE. If AE : EC = 4 : 7 and DE = 6.6 cm, find BC. If ‘x’ be the length of the perpendicular from A to DE, find the length of perpendicular from A to BC in terms of ‘x’.
Answer 5
In the given figure,
Question 6.
A line segment DE is drawn parallel to base BC of ΔABC which cuts AB at point D and AC at point E. If AB = 5 BD and EC = 3.2 cm, find the length of AE.
Answer 6
In ΔABC DE || BC
AB = 5 BD, EC = 3.2 cm
Question 7.
In the figure, given below, AB, CD and EF are parallel lines. Given AB = 7.5 cm, DC = y cm, EF = 4.5 cm, BC = x cm and CE = 3 cm, calculate the values of x
Answer 7
(i) In ΔACB and ΔFCE, we have
∠ACB = ∠FCE (vertically opposite angles)
∠CBA = ∠CEF (alternate angles)
ΔACB ~ ΔFCE (AA Axiom of similarity)
Thus their corresponding sides are proportional.
and y.


Question 8.
In the figure, given below, PQR is a right angle triangle right angled at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1 : 2. Calculate the lengths of PR and QR.
Answer 8
Given, PQ = 6 cm; PY = 4 cm;
PX : XQ = 1 : 2
Since a line drawn || to one side of triangle divide the other two sides proportionally.

Question 9.
In the following figure, M is mid-point of BC of a parallelogram ABCD. DM intersects the diagonal AC at P and AB produced at E. Prove that: PE = 2PD.
Answer 9
In the given figure, ABCD is a ||gm
AB || CD, AD || BC
M is mid point of BC
DM intersect AB produced at E and AC at P
To prove: PE = 2PD
Proof: In ΔDEA,
AD || BC (Opposite sides of || gm)
M is mid-point of CB B is mid-point of AE
AB = BE ⇒ AE = 2AB or 2CD
In ΔPAE and ΔPCD
∠APE = ∠CPD (Vertically opposite angles)
∠PAE = ∠PCD (Alternate angles)
Question 10.
The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.
Answer 10
In the given figure, ABCD is a ||gm E is a point on AD
CE is produced to meet BA produced at point F
AE = 4 cm, AF = 8 cm, AB = 12 cm
To find the perimeter of ||gm ABCD
In ΔFBC,
AD or AE || BC (Opposite sides of ||gm)
EXERCISE – 15 (C) Solutions of Concise Maths Chapter-15 Similarity with Map and Models
Question 1.
(i) The ratio between the corresponding sides of two similar triangles is 2 is to 5. Find the ratio between the areas of these triangles.
(ii) Areas of two similar triangles are 98 sq.cm and 128 sq.cm. Find the ratio between the lengths of their corresponding sides.
Answer 1

Question 2.
A line PQ is drawn parallel to the base BC, of ΔABC which meets sides AB and AC at points P and Q respectively. If AP = PB; find the value of:

Answer 2

Question 3.
The perimeters of two similar triangles are 30 cm and 24 cm. If one side of first triangle is 12 cm, determine the corresponding side of the second triangle.
Answer 3
Let we are given ΔABC and ΔPQR are similar.
Perimeter of ΔABC = 30 cm.
and perimeter of ΔPQR = 24 cm.
and side BC = 12 cm.
Now we have to find the length of QR, the corresponding side of ΔPQR
ΔABC ~ ΔPQR

Question 4.
In the given figure AX : XB = 3 : 5
Find :
(i) the length of BC, if length of XY is 18 cm.
(ii) ratio between the areas of trapezium XBCY and triangle ABC.
Answer 4
We are given in the ΔABC, AX : XB = 3 : 5
XY || BC.
Let AX = 3x and XB = 5x
AB = 3x + 5x = 8x.
Now in ΔAXY and ΔABC,
∠AXY = ∠ABC (corresponding angles)
∠A = ∠A (common)
ΔAXY ~ ΔABC (AA Postulate)

Question 5.
ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQ || BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP : AB.
Given- In ΔABC, PQ || BC in such away that area APQ = area PQCB
To Find- The ratio of BP : AB
Answer 5
In ΔABC, PQ || BC.
Z APQ = Z ABC (corresponding angles)
Now in ΔAPQ and ΔABC,
∠APQ = ∠ABC (proved)
∠A = ∠A (common)
ΔAPQ ~ ΔABC (AA postulate)

Question 6.
In the given triangle PQR, LM is parallel to QR and PM : MR = 3 : 4
calculate the value of ratio.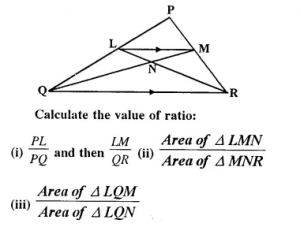
Answer 6
In ΔPQR, LM || QR in such away that PM : MR = 3 : 4
(i) In ΔPQR, LM || QR


Question 7.
The given diagram shows two isosceles triangles which are similar also. In the given diagram, PQ and BC are not parallel: PC = 4, AQ = 3, QB = 12, BC = 15 and AP = PQ.
Calculate-
(i) the length of AP
(ii) the ratio of the areas of triangle APQ and triangle ABC.
Answer 7

Question 8.
In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2. DP produced meets AB produced at Q. Given the area of triangle CPQ = 20 cm². Calculate
(i) area of triangle CDP
(ii) area of parallelogram ABCD [1996]
Answer 8
(i) Join QC.
In ΔBPQ and ΔCPD,
∠DPC = ∠BPQ (vertically opposite angles.)
∠PDC = ∠BQP (Alternate angles.)
ΔBPQ ~ ΔCDP (AA postulate)
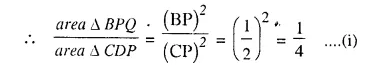
⇒ area ΔCDP = 4 (area ΔBPQ)
⇒ 2 (2 area ΔBPQ) = 2 x 20 = 40 cm² (2 area A BPQ = 20 cm²)
(ii) Area || gm ABCD = area ΔCPD + area ΔADQ – area ΔBPQ
= 40 + 9 (area BPQ) – area BPQ [(AD = CB = 3 BP)]
and = 40 + 8 (area ΔBPQ)
therefore = 40 + 8 (10) cm²
so = 40 + 80
Hence= 120 cm²
Question 9.
In the given figure. BC is parallel to DE. Area of triangle ABC = 25 cm². Area of trapezium BCED = 24 cm² and DE = 14 cm. Calculate the length of BC. Also. Find the area of triangle BCD.
Answer 9
In ΔADE, BC || DE
Area of ΔABC = 25 cm²
and area of trapezium BCED = 24 cm²
Area of ΔADE = 25 + 24 = 49 cm²
DE = 14 cm,
Let BC = x cm.
Now in ΔABC and ΔADE,
∠ABC = ∠ADE (corresponding angles)
∠A = ∠A (common)
ΔABC ~ ΔADE (AA postulate)

Question 10.
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5.
Find-
(i) ΔAPB : ΔCPB
(ii) ΔDPC : ΔAPB
(iii) ΔADP : ΔAPB
(iv) ΔAPB : ΔADB
Answer 10
AP : CP = 3 : 5 ⇒ =
(i) Now in ΔAPB and ΔCPB,
These triangles have same vertex and their bases are in the same straight line
area ΔAPB : area ΔCPB = AP : PC = 3 : 5 or ΔAPB : ΔCPB = 3 : 5
(ii) In ΔAPB and ΔDPC,
∠APB = ∠DPC (vertically opposite angles)
∠PAB = ∠PCD (alternate angles)
ΔAPB ~ ΔDPC (AA postulate)

⇒ area ΔDPC : area ΔAPB = 25 : 9 or ΔDPC : ΔAPB = 25 : 9
(iii) In ΔADP and ΔAPB,
There have the same vertex and their bases arc in the same straight line.
area ΔADP : area ΔAPB = DP : PB
But PC : AP = 5 : 3
ΔADP : ΔAPB = 5 : 3
(iv) Similarly area ΔAPB : area ΔADB = PB : DB = 3 : (3 + 5) = 3 : 8
Question 11.
In the given figure, ARC is a triangle. DE is parallel to BC and =
.
(i) Determine the ratios ,
(ii) Prove that ΔDEF is similar to ΔCBF.
Hence, find
(iii) What is the ratio of the areas of ΔDEF and ΔBFC?
Answer 11


Question 12.
In the given figure, ∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the ΔABC and ΔDEC.
Answer 12
In the figure DE = 7.8 cm, AB = 10.4 cm
∠ACD = ∠BCE (given)
Adding ∠DCB both sides,
∠ACD + ∠DCB = ∠DCB + ∠BCE
∠ACB = ∠DCE
Now in ΔABC and ΔDCE
∠B = ∠E (given)
∠ACB = ∠DCE (proved)
ΔABC ~ ΔDCE (AA axiom)
Question 13.
Triangle ABC is an isosceles triangle in which AB = AC = 13 cm and BC = 10 cm. AD is perpendicular to BC. If CE = 8 cm and EF ⊥ AB, find:
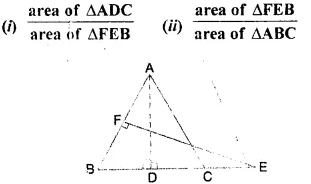
Answer 13
In the figure, ΔABC is an isosceles triangle in which
AB = AC = 13 cm, BC = 10 cm,
AD ⊥ BC, CE = 8 cm and EF ⊥ AB
(i) Now in ΔADC and ΔFEB
∠C = ∠B (AB = AC)
∠ADC = ∠EFB (each = 90°)
ΔADC ~ ΔFEB (AA axiom)

Similarity Solutions for Concise ICSE Maths Chapter-15, EX – 15 (D)
Question 1
A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A’ B’ C’. Calculate:
(i) the length of AB, if A’ B’ = 6 cm.
(ii) the length of C’ A’ if CA = 4 cm.
Answer 1
Scale factor (k) = 2.5
∆ABC is enlarged to ∆A’B’C’
(i) A’B’ = 6 cm
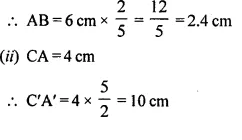
Question 2.
A triangle LMN has been reduced by scale factor 0.8 to the triangle L’ M’ N’. Calculate:
(i) the length of M’ N’, if MN = 8 cm.
(ii) the length of LM, if L’ M’ = 5.4 cm.
Answer 2
∆LMN has been reduced by the scale factor

Question 3.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find:
(i) A’ B’, if AB = 4 cm.
(ii) BC, if B’ C’ = 15 cm.
(iii) OA, if OA’= 6 cm.
(iv) OC’, if OC = 21 cm.
Also, state the value of:
(a)
(b)
Answer 3
∆ABC is enlarged to ∆A’B’C’ about the point O as its centre of enlargement.
Scale factor = 3 =

Question 4.
A model of an aeroplane is made to a scale of 1 : 400. Calculate:
(i) the length, in cm, of the model; if the length of the aeroplane is 40 m.
(ii) the length, in m, of the aeroplane, if length of its model is 16 cm.
Answer 4
Model of an aeroplane to the actual = 1 : 400

Question 5.
The dimensions of the model of a multistorey building are 1.2 m x 75 cm x 2 m. If the scale factor is 1 : 30; find the actual dimensions of the building.
Answer 5
Dimensions of a model of multistorey building = 1.2 m x 75 cm x 2 m

Question 6.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and angle ABC = 90°.
Calculate:
(i) the actual lengths of AB and BC in km.
(ii) the area of the plot in sq. km.
Answer 6
Scale of map drawn of a triangular plot = 1 : 2,50,000
Measurement of plot AB = 3 cm, BC = 4 cm
and ∠ABC = 90°

Question 7.
A model of a ship of made to a scale 1 : 300
(i) The length of the model of ship is 2 m. Calculate the lengths of the ship.
(ii) The area of the deck ship is 180,000 m². Calculate the area of the deck of the model.
(iii) The volume of the model in 6.5 m3. Calculate the volume of the ship. (2016)
Answer 7

Question 8.
An aeroplane is 30 in long and its model is 15 cm long. If the total outer surface area of the model is 150 cm², find the cost of painting the outer surface of the aeroplane at the rate of ₹ 120 per sq.m. Given that 50 sq. m of the surface of the aeroplane is left for windows.
Answer 8
Length of aeroplane = 30 m = 3000 cm
and length of its model = 15 cm
Surface area of model = 150 cm²
Scale factor (k) =![]() =
=![]()
Area of plane = k² x area of model = (200)² x 150 cm² = 40000 x 150 cm²
![]() = 600 m² (1 m² = 10000 cm²)
= 600 m² (1 m² = 10000 cm²)
Shape left for windows = 50 sq. m
Balance area = 600 – 50 = 550 sq. m
Race of painting the outer surface = ₹ 120 per sq.m
Total cost = ₹ 550 x 120 = ₹ 66000
Ex-15 (E), Selina Publishers Concise Solutions Chapter-15 Similarity for Map and Models
Question 1.
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.

Answer 1
In the given figure

Question 2.
In the following figure, ABCD to a trapezium with AB // DC. If AB = 9 cm, DC = 18 cm, CF= 13.5 cm, AP = 6 cm and BE = 15 cm. Calculate:
(i) EC
(ii) AF
(iii) PE
Answer 2
In the figure,
ABCD is a trapezium
AB || DC
AB = 9 cm, DC = 18 cm, CF = 13.5 cm AP = 6 cm and BE = 15 cm

Question 3.
In the following figure, AB, CD and EF are perpendicular to the straight line BDF.

Answer 3
In the given figure,
AB, CD and EF are perpendicular to the line BDF
AB = x, CD = z, EF = y
Question 4
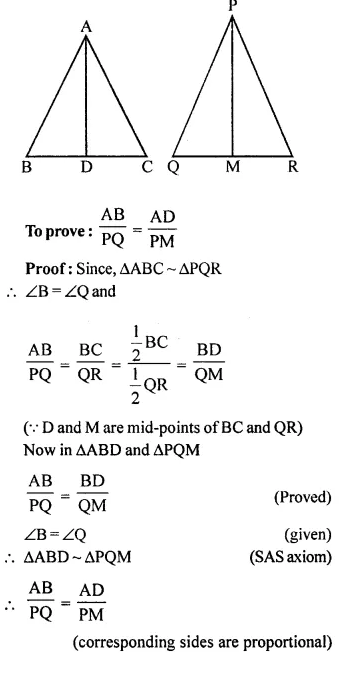
Triangle ABC is similar to triangle PQR. If AD and PM are corresponding medians of the two triangles, prove that:
Answer 4
∆ABC ~ ∆PQR
AD and PM are the medians of ∆ABC and ∆PQR respectively.
Question 5.
Triangle ABC is similar to triangle PQR. If AD and PM are altitudes of the two triangles, prove that:
Answer 5
Given, ∆ABC ~ ∆PQR
AD and PM are altitude of these two triangles

Question 6.
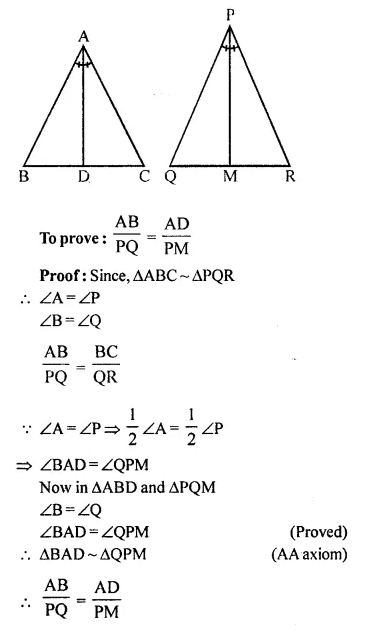
Triangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that: =
Answer 6
Given, ∆ABC ~ ∆PQR
AD and PM are the angle bisectors of ∠A and ∠P respectively.
Question 7.
Answer 7

Question 8. Concise Solutions Chapter-15 Similarity
Answer 8
In the given figure,
l || m || n
Transversal p and q intersects them at A, B, C and P, Q, R respectively as shown in the given figure.
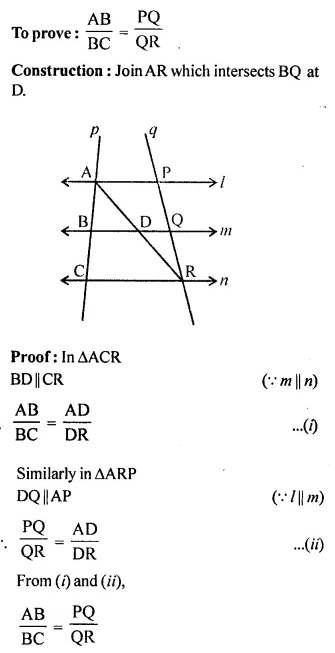
Question 9.

Answer 9

Question 10.
Calculate:
(i) EF
(ii) AC
Answer 10 Concise Solutions Chapter-15 Similarity
In the given figure,
AB || EF || CD
AB = 22.5 cm, EP = 7.5 cm
PC = 15 cm and DC = 27 cm

…
(i) ∆OAB ~ ∆OCD
(ii) ABCD is a trapezium.
Further if CD = 4.5 cm; find the length of AB.
In quadrilateral ABCD, diagonals AC and BD intersect each other at O and

Prove that: PM x PC = PN x PBGiven, AB = AC
Since equal sides has equal angle opposite to it
∠B = ∠C …(i)
In ∆PMB and ∆PNC, we have
∠B = ∠C [using (i)]
∠PMB = ∠PNC (each 90°)

Question 11.
(i) Prove that ∆ACD is similar to ∆BCA.
(ii) Find BC and CD.
(iii) Find area of ∆ACD : area of ∆ABC. (2014)
Answer 11
In ∆ACD and ∆BCA
∠C = ∠C (common)
∠ABC = ∠CAD (Given)
∆ACD = ∆BCA (by AA axiom)

Question 12.
Answer 12
Given : P and R the mid points of AB and AC respectively.
PR || BC and PR = BC = BQ.
PRQB is a || gm.
∠B = ∠PRQ ….(i)
Similarly, Q and R are the mid points of sides. BC and AC respectively
RQ || AB and QR = AB = AP
APQR is a ||gm.
∠A = ∠PQR ….(ii)
Similarly, we can prove that ∠C = ∠RPQ.
Now in ∆PQR and ∆ABC,
∠PQR = ∠A , ∠PRQ = ∠B and ∠RPQ = ∠C
(i) In ∆BCE
D is mid-point of BC and DF || CE
∆PQR ~ ∆ABC (AAA criterion of similarity)
Question 13. Concise Solutions Chapter-15 Similarity
(i) EF = FB
(ii) AG : GD = 2 : 1
Answer 13
Proof:
(i) In ∆BCE
D is the mid point of BC and DF || CE
E is mid-point of BE and EF = FB
(ii) AE = EB (E is mid point of AB)
and EF = FB (Proved)


Question 14.
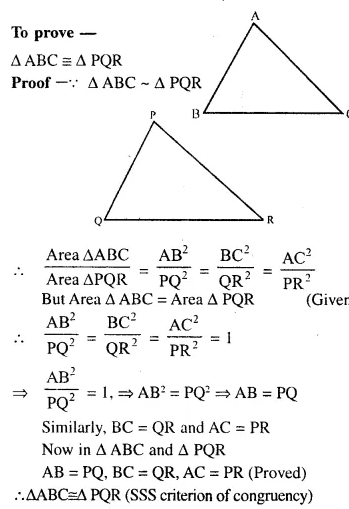
The two similar triangles are equal in area. Prove that the triangles are congruent.
Answer 14
Given : ∆ABC ~ ∆PQR and are equal in area
Question 15.
(i) medians
(ii) perimeters
(iii) areas
Answer 15
∆ABC ~ ∆DEF,
AL ⊥ BC and DM ⊥ EF
and AP and DQ are the medians and also
area ∆ABC : area ∆DEF = 16 : 25

Question 16. Concise Solutions Chapter-15 Similarity
(i) perimeters
(ii) altitudes
(iii) medians.
Answer 16
∆ABC ~ ∆DEF,
AL ⊥ BC and DM ⊥ EF
and AP and DQ are the medians and also
area ∆ABC : area ∆DEF = 16 : 25

Question 17.
(i) triangle PQR.
Answer 17
In ∆PQR, XY || QR and PX : XQ = 1 : 3, QR = 9 cm.

Question 18.
On a map, drawn to a scale of 1 : 20000, a rectangular plot of land ABCD has AB = 24 cm, and BC = 32 cm. Calculate :
(i) The diagonal distance of the plot in kilometre
(ii) The area of the plot in sq. km.
Answer 18

Question 19.
(i) the floor area of a room of the building, if the floor area of the corresponding room in the model is 50 sq cm.
(ii) the space (volume) inside a room of the model, if the space inside the corresponding room of the building is 90 m3.
Answer 19
The scale factor is 1 : 50 or k =
Dimension of the building = 100 cm x 60 cm x 120 cm.
k x actual dimensions of the building = Dimension of the model.
Question 20. Concise Solutions Chapter-15 Similarity
(i) ∆PQL ~ ∆RPM
(ii) QL x RM = PL x PM
(iii) PQ² = QR x QL [2003]
Answer 20
(i) In ∆PQL and ∆RPM
∠PQL = ∠RPM (Given)
∠LPQ = ∠MRP (Given)
∆PQL ~ ∆RPM (AA criterion of similarity)
(ii) ∆PQL ~ ∆RPM (Proved)


Question 21.
Answer 21
In ∆ABC.
AB = 3 cm. BC = 6 cm and AC = 4 cm
In ∆DEF,
Longest side EF = 9 cm
and longest side in ∆ABC is BC = 6 cm
Question 22.
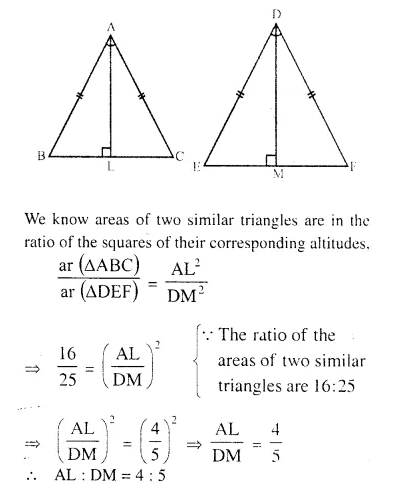
Two isosceles triangles have equal vertical angles. Show that the triangles are similar. If the ratio between the areas of these two triangles is 16 : 25, find the ratio between their corresponding altitudes.
Answer 22
Let in two ∆ABC and ∆DEF
The vertical angles of two isosceles triangles are equal i.e. ∠A = ∠D
But AB = DE and AC = DF (isosceles ∆s)
Then base angles are also equal (Angles opposite to equal sides)
The two triangles are similar.
∆ABC ~ ∆DEF
Let AL ⊥ BC and DM ⊥ EF
Question 23.
(ii) area ∆APO : area ∆CQO.
Answer 23
In ∆ABC,
AP : PB = 2 : 3
PQ || BC and CQ || BA


Question 24.
(i) ∆ADC ~ ∆BEG
(ii) CA x CE = CB x CD
(iii) ∆ABC ~ ∆DEC
(iv) CD x AB = CA x DE
Answer 24
In ∆ABC, AD ⊥ BC and BE ⊥ AC, DE is joined
To prove:
(i) ∆ADC ~ ∆BEG
(ii) CA x CE = CB x CD
(iii) ∆ABC ~ ∆DEC
(iv) CD x AB = CA x DE
Proof:
(i) In ∆ADC and ∆BEC,
∠C = ∠C (common)
∠ABE = ∠BEC (each 90°)
∆ADC ~ ∆BEC (AA axiom)

Question 25.
If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ∆BED = 9 cm². Calculate the
(i) length of AB
(ii) area of ∆ABC
Answer 25
In ∆ABC and ∆EBD
∠1 = ∠2 (given)
∠B = ∠B (common)

Question 26 Concise Solutions Chapter-15 Similarity
(i) Prove ∆ADB ~ ∆CDA.
(ii) If BD = 18 cm, CD = 8 cm, find AD.
(iii) Find the ratio of the area of ∆ADB is to area of ∆CDA.
Answer 26
(i) In ∆ADB and ∆CDA :
∠ADB = ∠ADC [each = 90°]
∠ABD = ∠CAD [each = 90° – ∠BAD]
∆ADB ~ ∆CDA [by AA similarity axiom]
(ii) Since, ∆ADB ~ ∆CDA
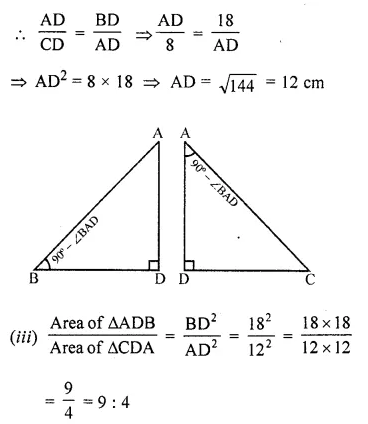
Question 27
(i) Prove that ∆ABC ~ ∆DEC
(ii) If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
(iii) Find the ratio of the area of ∆ABC : area of ∆DEC.
Answer 27
(i) To prove : ∆ABC ~ ∆DEC
In ∆ABC and ∆DEC
∠ABC = ∠DEC = 90°
∠C = ∠C (common)
∆ABC ~ ∆DEC (by AA axiom)

Question 28.
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
(iii) Find, area of ∆ADE : area of quadrilateral BCED. (2015)
Answer 28
In the given figure,
∆ABC is right angled triangle right angle at B.
D is any point on AB and DE ⊥ AC
To prove:
(i) ∆ADE ~ ∆ACB.
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm.Find DE and AD.
(iii) Find, area of ∆ADE : area of quadrilateral BCED
Proof:
(i) In ∆ADE and ∆ACB
∠A = ∠A (common)
∠E = ∠B (each = 90°)
∆ADE ~ ∆ACB. (AAaxiom)
(ii) AC = 13 cm, BC = 5 cm, AE = 4 cm
∆ADE ~ ∆ACB.

Question 29. Concise Solutions Chapter-15 Similarity

Answer 29
In the given figure, AB || DE, BC || EF

Question 30

Answer 30

–:End of Concise Solutions Chapter-15 Similarity :–
Return to :- Concise Selina Maths Solutions for ICSE Class-10
Thanks
Please share with your friends