Concise Solutions Mensuration Chapter-20 ICSE Maths Class 10. Selina Concise Solutions of Exercise – 20 (A), Exercise – 20 (B), Exercise – 20 (C), Exercise – 20 (D), Exercise – 20 (E), Exercise – 20 (F)and Exercise-20(G) . Concise Maths Solutions Mensuration Chapter-20 for ICSE Maths Class 10 is available here. Solutions of Concise Selina Maths of Mensuration Chapter-20 has been solved according instruction given by council. This is the Solutions of Mensuration Chapter-20 for ICSE Class 10th. ICSE Maths text book of Concise Selina Publishers is In series of famous ICSE writer in maths publications. Concise is most famous among students.
Concise Solutions Mensuration Chapter-20 Maths Class 10
This Post is the Solutions of Concise Mathematics Mensuration Chapter-20 for ICSE Class 10. Experience teachers Solved Chapter-20 Mensuration to help students of class 10th ICSE board.
–:Select Topic :–
Combination, Exercise –20 (E),
How to Solve Concise Maths Selina Publications Chapter-17 Circles ICSE Maths Class 10
Before viewing Solutions of Mensuration Chapter-20 of Concise Selina Maths . Read the Chapter Carefully then solve all example of your text book. The Chapter-20 Mensuration is formula Based Chapter.
EXERCISE – 20 (A) Mensuration – Cylinder, Cone and Sphere ( Surface , Area and Volume) Concise Selina Maths Solutions Chapter-20 ICSE Board Class 10
Question 1.
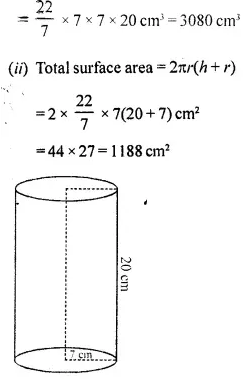
(i) the volume
(ii) the total surface area.
Answer 1
Height of cylinder (h) = 20cm
and radius of its base (r) = 7 cm
(î) Volurne=πr²h
Question 2.
The inner radius of a pipe is 2.1 cm. How much water can 12 m of this pipe hold ?
Answer 2
Inner radius of a pipe (r) = 2.1 cm
and length of pipe (h) = 12 m = 1200 cm
∴ Volume of water in it = πr2h
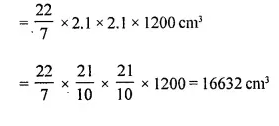
Question 3.
A cylinder of circumference 8 cm and length 21 cm roils without sliding for 4 seconds at the rate of 9 complete rounds per second. Find:
(i) the distance travelled by the cylinder in 4 seconds, and
(ii) the area covered by the cylinder in 4 seconds.
Answer 3
Circumference of a cylinder = 8 cm

Question 4.
How many cubic metres of earth must be dug out to make a well 28 m deep and 2.8 m in diameter ? Also, find the cost of plastering its inner surface at ₹4.50 per sq. metre.
Answer 4

Question 5.
What length of solid cylinder 2 cm in diameter must be taken to recast into a hollow cylinder of external diameter 20 cm, 0.25 cm thick and 15 cm long ?
Answer 5
Diameter of solid cylinder = 2 cm
∴ Radius (r) = = 1 cm
Let length (h) = x cm
∴ Volume = πr²h = π x 1 x 1 x x
= πx cm3 …(i)
External diameter of hollow cylinder = 20cm
∴ External radius = = 10 cm
Thickness of cylinder = 0.25 cm
∴ Innerradius= 10-0.25 = 9.75 cm
Length = 15 cm
∴ Volume = π(R2 – r2) x h
= π(R + r)(R-r) x h
= π(10 + 9.75)(10-9.75) x 15 cm3
= πx 19.75 x 0.25 x 15 cm3 ………(ii)
Comparing (i) and (ii), we get
∴ π x 19.75 x 0.25 x 15 = π x
x = 19.75 x 0.25 x 15 cm
= 74.0625 = 74.06 cm
Question 6.
A cylinder has a diameter of 20 cm. The area of the curved surface is 100 cm2 (sq. cm). Find:
(i) the height of the cylinder correct to one decimal place.
(ii) the volume of the cylinder correct to one decimal place.
Answer 6

Question 7.
A metal pipe has a bore (inner diameter) of 5 cm. The pipe is 5 mm thick all round. Find the weight, in kilogram, of 2 metres of the pipe if 1 cm3 of the metal weighs 7.7 g.
Answer 7

Question 8.
A cylindrical container with diameter of base 42 cm contains sufficient water to submerge a rectangular solid of iron with dimensions 22 cm x 14 cm x 10.5 cm. Find the rise in the. level of the water when the solid is submerged.
Answer 8
Diameter of base of a cylindrical container =42 cm
∴ Radius = = 21 cm
Size of rectangular solid = 22cmx 14cmx 10.5 cm
∴ Volume of solid = 3234 cm3
∴ Height of water level raise in the container
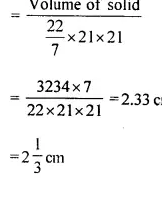
Question 9.
A cylindrical container with infernal radius of its base 10 cm’, contains water up”to a height of 7 cm. Find the area of the wet surface of the cylinder.
Answer 9
Internal radius of cylindrical container (r) = 10cm
Water upto height (h) = 7 cm
∴ Area of wet surface by the water of the container = 2πrh
= π x 19.75 x 0.25 x 15 cm3 …(ii)
Comparing (i) and (ii), we get
∴ π x 19.75 x 0.25 x 15 = πx
x = 19.75×0.25x 15 cm
= 74.0625
= 74.06 cm
Question 10.
Find the total surface area of an open pipe of length 50 cm, external diameter 20 cm and internal diameter 6 cm.
Answer 10
Length of open pipe (h) = 50 cm
External diameter=20 cm
and internal diameter = 6 cm

Question 11.
The height and the radius of the base of a cylinder are in the ratio 3:1. If its volume is 1029 πcm3; find its total surface area.
Answer 11
Ratio between height and radius of a cylinder = 3:1
Volume = …….(i)
Let radius of the base = r
then height = 3r

Question 12.
The radius of a solid right circular cylinder increases by 20% and its height decreases by 20%. Find the percentage change in its volume.
Answer 12
Let radius of the cylinder (r) = 100 cm
and height (h) = 100 cm
∴ Volume = πr2h =π( 100)2 x 100 cm3 = 1000000π cm3
Now radius (R) = 100 + 20 = 120 cm
and new height (h) = 100 – 20 = 80 cm
∴ Volume = π(120)2 x 80
= π x 14400 x 80cm3= 152000π cm3
Percentage change (increase) in the volume

Question 13.
The radius of a solid right circular cylinder decreases by 20% and its height increases by 10%. Find the percentage change in its:
(i) volume
(ii) curved surface area
Answer 13
Let radius of the cylinder = 100 cm
and height = 100 cm
∴ Volume = πr2h
= πx 100 x 100 x 100 cm3
= 1000000πcm3
and Curved surface area = 2πrh
= 2 x π x 100 x 100 cm2
=20000π cm2
Decreased radius = 100 – 20 = 80 cm
and increased height = 100 + 10 = 110 cm
∴ Increased volume = π x 80 x 80 x 110 cm3 = 704000π cm3
and increased curved surface =2 x π x 80 x 110 cm2 = 17600πcm2
⇒ Decrease in volume = 1000000π – 704000π = 296000π cm3

Question 14.
Find the minimum length in cm and correct to nearest whole number of the thin metal sheet required to make a hollow and closed cylindrical box of diameter 20 cm and height 35 cm. Given that the width of the metal sheet is 1 m. Also, find the cost of the sheet at the rate of ₹56 per m.
Find the area of metal sheet required, if 10% of it is wasted in cutting, overlapping, etc.
Answer 14
Diameter of the hollow closed cylinder =20 cm
∴ Radius (r) =
and height (h) = 35 cm

Question 15.
3080 cm3 of water is required to fill a cylindrical vessel completely and 2310 cm3 of water is required to fill it upto 5 cm below the top. Find:
(i) radius of the vessel.
(ii) height of the vessel.
(iii) wetted surface area of the vessel when it is half-filled with water.
Answer 15
Volume of water to fill a cylindrical vessel = 3080 cm3
Volume of water to fill it upto 5 cm below = 2310 cm2
Volume of water for 5 cm height =3080- 2310 = 770cm3

Question 16.
Find the volume of the largest cylinder formed when a rectangular piece of paper 44 cm by 33 cm is rolled along it:
(i) shorter side.
(ii) longer side.
Answer 16
Length of rectangular sheet = 44 cm
and breadth = 33 cm

Question 17.
A metal cube of side 11 cm is completely submerged in water contained in a cylindrical vessel with diameter 28 cm. Find the rise in the level of water.
Answer 17
Side of a cube = 11 cm
∴ Volume = (Side)3 = 11 x 11 x 11 cm3 = 1331 cm3
Diameter of cylinder = 28 cm

Question 18.
A circular tank of diameter 2 m is dug and the earth removed is spread uniformly all around the tank to form an embankment 2 m in width and 1.6 m in height. Find the depth of the circular tank.
Answer 18
Diameter of circular tank = 2m
Width of embankment = 2 m
Height = 1.6 m

Question 19.
The sum of the inner and the outer curved surfaces of a hollow metallic cylinder is 1056 cm2 and the volume of material in it is 1056 cin3. Find its internal and external radii. Given that the height of the cylinder is 21 cm.
Answer 19
Sum of outer and inner surface area of a hollow cylinder = 1056 cm2
Volume of metal used =1056 cm3
Height of cylinder (h) = 21 cm
Let outer radius = R
and inner radius = r
Height = 21 cm
We are given
Outer surface + Inner surface = 1056 cm2
Volume = πR2h – πr2h =1056 cm3
Now, 2πRh + 2πrh =1056

Question 20.
The difference between the outer curved surface area and the inner curved surface area of a hollow cylinder is 352 cm2. If its height is 28 cm and the volume of material in it is 704 cm3; find its external curved surface area.
Answer 20
Difference in outer and inner curved surface of a hollow cylinder = 352 cm2
Height (h) = 28 cm
Volume of material used = 704 cm3
Let outer radius = R
and inner radius = r
∴ 2πRh-2πrh = 352
2πh(R-r) = 352

Question 21.
The sum of the height and the radius of a solid cylinder is 35 cm and its total surface area is 3080 cm2; find the volume of the cylinder.
Answer 21

Question 22.
The total surface area of a solid cylinder is 616 cm2. If the ratio between its curved surface area and total surface area is 1:2; find the volume of the cylinder.
Answer 22
Total surface area of a cylinder = 616 cm2

Question 23.
A cylindrical vessel of height 24 cm and diameter 40 cm is full of water. Find the exact number of small cylindrical bottles, each of height 10 cm and diameter 8 cm, which can be filled with this water.
Answer 23
Height of cylinder (6) = 24 cm
Radius (r)= = 20 cm
∴ Volume of water filled in it = πr2h
= π x 20 x 20 x 24 cm3
= 9600π cm3
Radius of small cylindrical bottle = = 4 cm
and height (6) = 10 cm
∴ Volume of one small bottle = πr2h
π x 4 x 4 x 10 cm3 = 160π cm3
∴ Number of small bottles

Question 24.
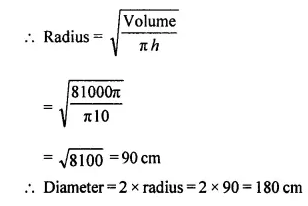
Two solid cylinders, one with diameter 60 cm and height 30 cm and the other with radius 30 cm and height 60 cm, are melted and recasted into a third solid cylinder of height 10 cm. Find the diameter of the cylinder formed.
Answer 24
Diameter of first cylinder = 60 cm
∴ Radius (R)= =30 cm
and height (h) = 30 cm
Radius of second cylinder = 30 cm
and height = 60 cm
Volume of first cylinder = πR2h
= π30 x 30 x 30 cm3 = 27000π cm3
and volume of second cylinder = π x 30 x 30 x 60 cm3 = 54000πcm3
Total volume of both cylinders
= 27000π+ 54000π cm3
= 81000π cm3
Volume of third cylinder = 81000π cm3
Height of third cylinder = 10 cm
Question 25.
The total surface area of a hollow cylinder, which is open from both the sides, is 3575 cm2; area of its base ring is 357.5 cm2 and its height is 14 cm. Find the thickness of the cylinder.
Answer 25
Total surface area of an opened hollow cylinder = 3575 cm2
Area of ring of its base = 357.5 cm2
Height = 14 cm
Let R and r be the outer and inner radius of the ring.
∴ π(R2 – r2) = 357.5

Question 26.
The given figure shows a solid formed of a solid cube of side 40 cm and a solid cylinder of radius 20 cm and height 50 cm attached to the cube as shown.
Find the volume and the total surface area of the whole solid [Take π=3.14]
Answer 26
Side of the cube = 40 cm
Radius of cylinder = 20 cm
Height (h) = 50 cm
Volume of cube = (40)3 = 64000 cm3
and volume of cylinder = πr2h
= 3.14 x 20 x 20 x 50 cm3
=314×200 = 62800 cm3
∴ Total volume = 64000 + 62800 =126800cm3
Total surface area = (6a2 + 2πrh)
= 6 x 40 x 40 + 2 x 3.14 x 20 x 50 =9600+6280
= 15880 cm2
Question 27.
Two right circular solid cylinders have radii in the ratio 3: 5 and heights in the ratio 2:3. Find the ratio between their:
(i) curved surface areas.
(ii) volumes.
Answer 27
The ratio is the radii of two right circular solid cylinder = 3:5
and ratio in their heights = 2:3
(i) Let radius of first cylinder = 3x
and height = 2y
∴ Curved surface area = 2πrh
= 2π(3x) (2y) = 12 πxy
and radius of second cylinder = 5x
and height = 3y
∴ Curved surface = 2πrh
= 2π x 5x 3y
= 30πxy
∴ Ratio in their curved surface
= 12πxy : 30πxy
= 2 :5
(ii) Volume of first cylinder = πr2h
= π(3x)2 x 2y = 18πx2y
and volume of second cylinder = π(5x)2 x 3y
= 75πx2y
∴ Ratio = 18πx2y : 75πx2y
= 6:25
Question 28.
A closed cylindrical tank, made of thin iron sheet, has diameter = 8.4 m and height 5.4 m. How much metal sheet, to the nearest m2, is used in making this tank, if of the sheet actually used was wasted in making the tank ?
Answer 28
Diameter of a closed cylindrical tank=8.4 cm
∴ Radius (r) = = 4.2 m
and height (h) = 5.4 m
∴ Total surface area = 2πr(r + h)
= 2 x x 4.2(4.2+ 5.4) m2
=26.4 x 9.6 m2=253.44 m2
Area of sheet used in wastage
= of 253.44= 16.896 m2
Total sheet required = 16.896 +253.44 m2
= 270.336 m2
=270.34 m2 (approx)
Mensuration – Cylinder, Cone and Sphere ( Surface , Area and Volume) EXERCISE – 20 (B) Selina Concise Maths Solutions Chapter-20 ICSE Board Class 10
Question 1.
Find the volume of a cone whose slant height is 17 cm and radius of base is 8 cm.
Answer 1
Slant height (L) = 17 cm
Radius (r) = 8cm
But l2= r2 + h2
⇒ h2 = l2-r2 = 172 – 82
⇒ h2 = 289 – 64 = 225 = (15)2
∴ h=15 cm.
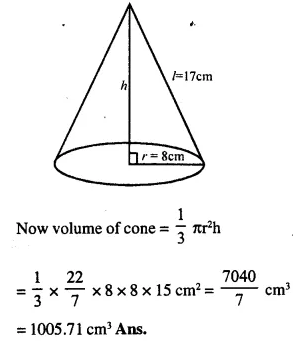
Question 2.
Answer 2
Curved surface area = 12320 cm2
Radius of base (r) = 56 cm.
Let slant height = l.
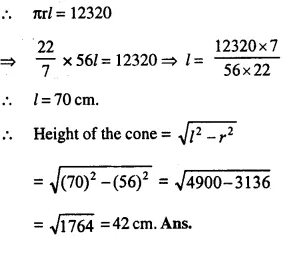
Question 3.
Answer 3
Circumference of conical tent = 66 m
and height (h) = 12 m.

Question 4.
Answer 4
The ratio between radius and height = 5 : 12
Volume =2512 cm3
Let radius (r) = 5x and
height (h) = 12x
and slant height = l

Question 5.
Answer 5
Let radius of cone y = r
∴ radius of cone x = 3r
Let volume of cone y = V
Then volume of x = 2V
Let h1 be the height of x and h2 be the height of y.

Question 6.
Answer 6
Let radius of each one = r
and ratio between their slant heights =5:4
Let slant height of the first cone = 5x
and slant height of second = 4 x
∴ Curved surface area of the first cone
= πr = πr x 5x = 5πrx.
and curved suface area of second cone
= πr x 4x = 4πrx
∴ Ratio between them = 5 πrx : 4 πrx
= 5:4
Question 7.
There are two cones. The curved surface area of one is twice that of the other. The slant height of the latter is twice that of the former. Find the ratio of their radii.
Answer 7
Let the slant height of first cone = l
then slant height of the second cone = 2l
and let r1 be the radius of the first cone and r2 be the radius of the second cone.
Then curved surface area of the first cone = πr1l
and that of second cone = πr22l= 2πr2l.
According to the condition,
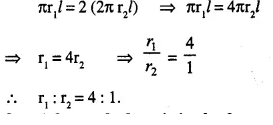
Question 8.
A heap of wheat is in the form of a cone of diameter 16.8 m and height 3.5m. Find its volume. How much cloth is required to just cover the heap?
Answer 8

Question 9.
Answer 9

Question 10.
A solid cone of height 8 cm and base radius 6 cm is melted and recast into identical cones, each of height 2 cm and diameter 1 cm. Find the number of cones formed.
Answer 10
Height of solid cone (h) = 8 cm.
Radius (r) = 6 cm.

Question 11.
(i) its radius in cm
(ii) its volume in cm3. [Take π = 3.14]
Answer 11
Total surface area of cone = 90π cm2
slaint height (l) = 13 cm
Let r be its radius, then
Total surface area = πrl + πr2 = πr (l + r)

Question 12.
The area of the base of a conical solid is 38.5 cm2 and its volume is 154 cm3. Find curved surface area of the solid.
Answer 12
Area of base of a solid cone = 38.5 cm2
and volume = 154 cm3
Question 13.
A vessel, in the form of an invested cone, is filled with water to the brim. Its height is 32 cm and diameter of the base is 25.2 cm. Six equal solid cones are dropped in it, so that they are fully submerged. As a result, one-fourth of water in the original cone overflows. What is the volume of each of the solid cones submerged ?
Answer 13
Diameter of the base of cone = 25.2 cm

Question 14.
The volume of a conical tent is 1232 m3 and the area of the base floor is 154 m2. Calculate the:
(i) radius of the floor.
(ii) height of the tent.
(iii) length of the canvas required to cover this conical tent if its width is 2 m. (2008)
Answer 14
Volume of conical tent = 1232 m3
Area of base floor = 154 m2
(i) Let r be the radius of the floor
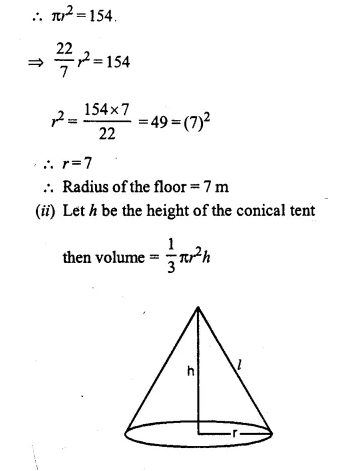
Mensuration – Cylinder, Cone and Sphere ( Surface , Area and Volume) Concise Selina Maths Solutions Chapter-20, Exercise 20(C)
Question 1.
The surface area of a sphere is 2464 cm2, find its volume.
Answer 1
Surface area of sphere = 2464 cm2
Let radius = r
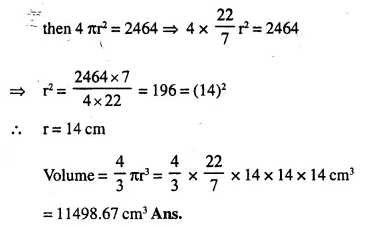
Question 2.
The volume of a sphere is 38808 cm3; find its diameter and the surface area.
Answer 2
Volume of sphere = 38808 cm3
Let radius of shpere = r

Question 3.
A spherical ball of lead has been melted and made into identical smaller balls with radius equal to half the radius of the original one. How many such balls can be made ?
Answer 3
Let the radius of spherical ball = r
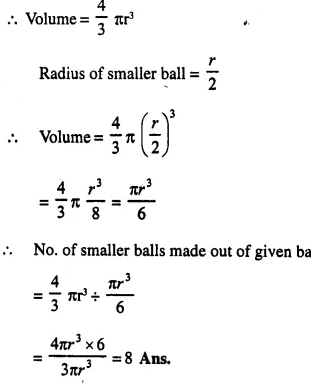
Question 4.
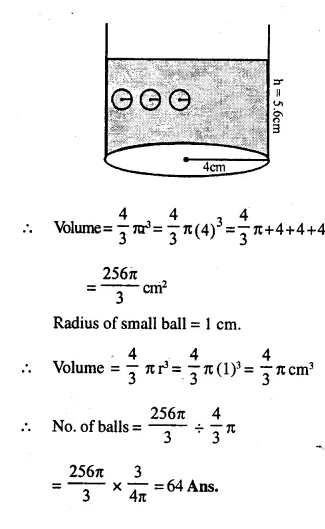
How many balls each of radius 1 cm can be made by melting a bigger ball whose diameter is 8 cm.
Answer 4
Question 5.
Eight Metallic sphere; each of radius 2 mm, are melted and cast into a single sphere. Calculate the radius of the new sphere.
Answer 5
Radius of metallic sphere = 2mm = cm

Question 6.
The volume of one sphere is 27 times that of another sphere. Calculate the ratio of their:
(i) radii,
(ii) surface areas.
Answer 6
Volume of first sphere = 27 x volume of second sphere.
Let radius of first sphere = r1
and radius of second sphere = r2

Question 7.
If the number of square centimetres on the surface of a sphere is equal to the number of cubic centimetres in its volume, what is the diameter of the sphere ?
Answer 7

Question 8.
A solid metal sphere is cut through its centre into 2 equal parts. If the diameter of the sphere is 3 cm, find the total surface area of each part correct to two decimal places.
Answer 8
A solid sphere is cut into two equal hemispheres.

Question 9.
The internal and external diameters of a hollow spectively. Find:
(i) internal curved suface area,
(ii) external curved surface area,
(iii) total surface area,
(iv) volume of material of the vessel.
Answer 9
Internal diameter of hollow hemispher = 21cm
and external diameter = 28 cm


Question 10.
A solid sphere and a solid hemi-sphere have the same total surface area. Find the ratio between their volumes.
Answer 10
Let radius of a sphere = R
∴ Surface area = 4πR2
and radius of hemi-sphere = r
∴ Surface area = 3πr2
∵ Their surface area are equal
4πR2 = 3πr2 ⇒ 4R2 = 3r2

Question 11.
Metallic spheres of radii 6 cm, 8 cm and 10 cm respectively are melted and recasted into a single solid sphere. Taking π = 3.1, find the surface area of solid sphere formed.
Answer 11
Radius of first sphere (r1) = 6 cm
Radius of second sphere (r2) = 8 cm
Radius of third sphere (r3) = 10 cm

Question 12.
The surface area of a solid sphere is increased by 21% without changing its shape. Find the percentage increase in its:
(i) radius
(ii) volume
Answer 12
(i) Let r be the radius of the solid sphere then surface area = 4πr2
Increase in area = 21%

Mensuration – Cylinder, Cone and Sphere ( Surface , Area and Volume) EXERCISE – 20 (D) Concise Selina Maths Solutions Chapter-20
Question 1.
A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast.
Answer 1
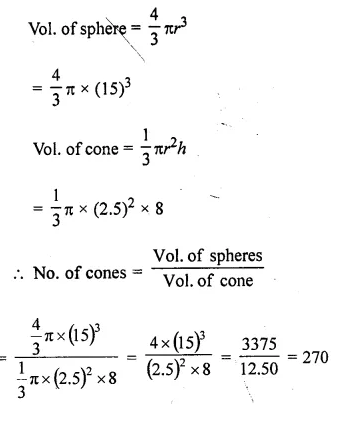
Question 2.
Answer 2
Mensuration Ex 20 D Ans 12External diameter = 8cm
∴ Radius (R) = = 4 cm
Internal diameter = 4 cm
∴ Radius (r) = = 2cm.
Volume of metal used in hollow sphere

Question 3. Concise Solutions Mensuration Chapter-20
The radii of the internal and external surfaces of a metallic spherical shell are 3 cm and 5 cm respectively. It is melted and recast into a solid right circular cone of height 32 cm. Find the diameter of the base of the cone.
Answer 3
Inner radius of spherical shell (r) = 3 cm
and outer radius (R) = 5 cm

Question 4.
Answer 4
Height of bigger cone (H) = 9 cm
Diameter 40 cm

Question 5.
Answer 5
Dimensions of rectangular block of metal = 49cm x 44 cm x 18 cm.
∴ Volume = 49 x 44 x 18 cm3 = 38808 cm3
Let radius of solid sphere = r

Question 6.
A hemisphere bowl of internal radius 9 cm is full of liquid. This liquid is to be filled into conical shaped small containers each of diameter 3 cm and height 4 cm. How many containers are necessary to empty the bowl?
Answer 6
Internal radius of hemispherical bowl (r) = 9 cm

Question 7.Concise Solutions Mensuration Chapter-20
A hemispherical bowl of diameter 7.2 cm is filled completely with chocolate sauce. This sauce is poured into an inverted cone of radius 4.8 cm. Find the height of the cone if it is completely filled. [2010]
Answer 7
Diameter of hemispherical bowl = 7.2 cm

Question 8.
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres of radius 0.5 cm. Find the number of spheres formed. [2011]
Answer 8
Radius of solid cone = (r) = 5 cm
and height (h) = 8 cm

Question 9.
The total area of a solid metallic sphere is 1256 cm2. It is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate:,
(i) the radius of the solid sphere,
(ii) the number of cones recast. Take π = 3.14 [2000]
Answer 9
Total area of solid sphere = 125

Question 10.
A solid metallic cone, with radius 6 cm and height 10 cm, is made of some heavy metal A. In order to reduce its weight, a conical hole is made in the cone as shown and it is completely filled with a lighter metal B. The conical hole has a diameter of 6 cm and depth 4 cm. Calculate the ratio of the volume of metal A to the volume of the metal B in the solid.
Answer 10
Radius of solid metallic cone A(R) = 6 cm
and height (H) = 10 cm

Question 11. Concise Solutions Mensuration Chapter-20
A hollow sphere of internal and external radii 6 cm and 8 cm respectively is melted and recast into small cones of base radius 2 cm and height 8 cm. Find the number of cones. [2012]
Answer 11
Inner radius of a hollow sphere (r) = 6 cm
and outer radius (R) = 8 cm

Question 12.
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate:
(i) the radius of the sphere.
(ii) the number of cones recast. (Take π = 22/7)
Answer 12
(i) Surface area=4πr2=2464 cm2 (given)
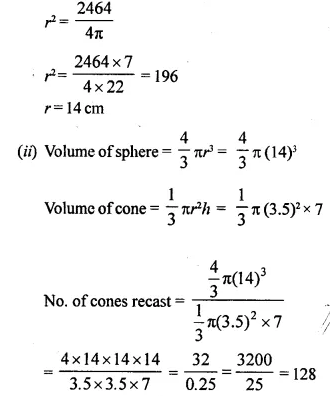
EXERCISE – 20 (E) Concise Selina Solutions Mensuration Chapter-20 Surface area and Volume of Cone Cylinder sphere
Question 1.
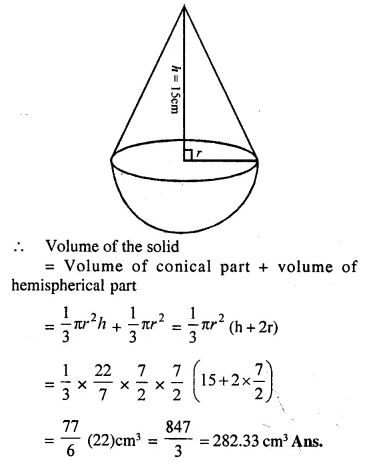
A cone of height 15 cm and diameter 7 cm is mounted on a hemisphere of same diameter. Determine the volume of the solid thus formed.
Answer 1
Height of cone = 15 cm
and radius of base = cm.
Question 2.Concise Solutions Mensuration Chapter-20
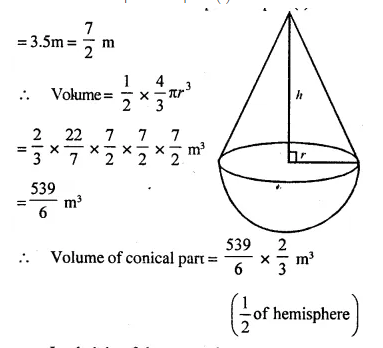
A buoy is made in the form of hemisphere surmounted by a right, cone whose circular base coincides with the plane surface of hemisphere. The radius of the base of the cone is 3.5 metres and its volume is two-thirds of the hemisphere. Calculate the height of the cone and the surface area of the buoy, correct to two places of decimal.
Answer 2
Radius of hemispherical part (r)
Question 3.
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find:
(i) the surface area of remaining solid,
(ii) the volume of remaining solid,
(iii) the weight of the material drilled out if it weighs 7 gm per cm3.
Answer 3
Length of rectangular solid (l) = 30 cm
Breadth (b) = 20 cm
and height (h) = 42 cm
Diameter of the cone = 14 cm


Question 4.
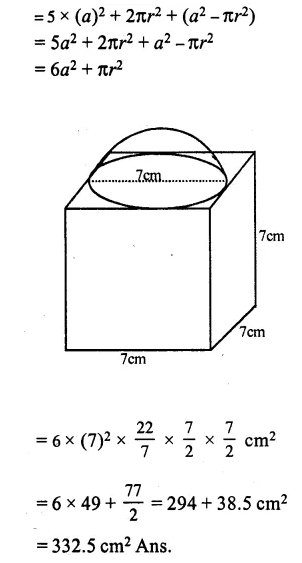
A cubical block of side 7 cm is surmounted by a hemisphere of the largest size. Find the surface area of the resulting solid.
Answer 4
Side of a cubical block = 7 cm
Radius of the hemisphere = cm
Now total surface area of the block
Question 5.Concise Solutions Mensuration Chapter-20
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the rim. When lead shots each of which is a sphere of radius 0.5 cm are dropped into the vessel, one- fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Answer 5
Radius of conical vessel (R) = 5 cm
and height (h) = 8 cm

Question 6.
A hemi-spherical bowl has neligible thickness and the length of its circumference is 198 cm. Find the capacity of the bowl.
Answer 6
Upper circumference of the hemi-spherical bowl = 198 cm

Question 7.
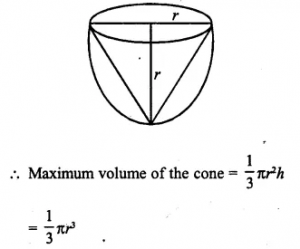
Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r cm.
Answer 7
Radius of solid hemisphere = r
Radius of the cone carved out of the hemisphere = r
and height (h) = r
Question 8.
The radii of the bases of two solid right circular cones of same height are r1 and r2 The cones are melted and recast into a solid sphere of radius R. Find the height of each cone in terms of r1, r2 • and R.
Answer 8

Question 9.Concise Solutions Mensuration Chapter-20
A solid metallic hemisphere of diameter 28 cm is melted and recast into a number of identical solid cones, each of diameter 14 cm and height 8 cm. Find the number * of cones so formed.
Answer 9
Diameter of solid hemisphere = 28 cm

Question 10.
A cone and a hemisphere have the same base and the same height. Find the ratio between their volumes.
Answer 10
Let radius of the base of cone = r
and height = h
Then radius of hemisphere = r
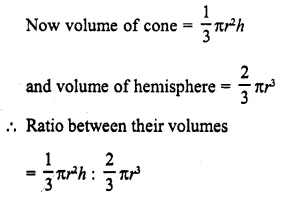
Concise Solutions of Chapter-20 Mensuration EXERCISE – 20 (F)
Question 1.
From a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and same base is removed. Find the volume of the ramaining solid.
Answer 1
Height of the cylinder (h) = 10 cm
and radius of base (r) = 6 cm.
∴ Volume of cylinder = πr2h
Height of cone = 10 cm
and radius of base of cone = 6 cm

Question 2.
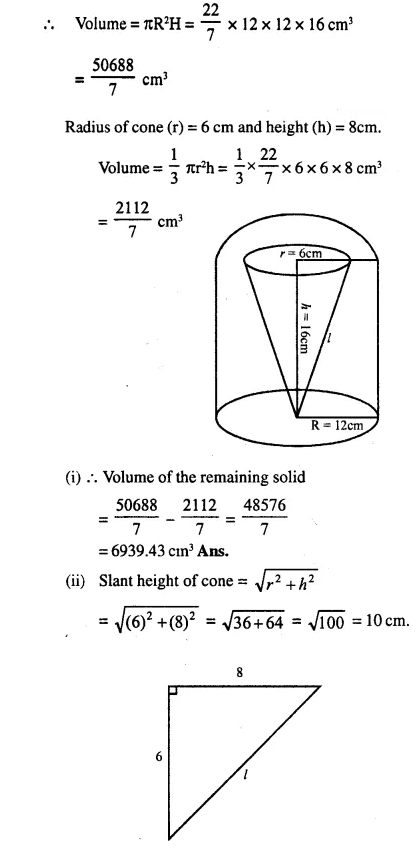
From a solid cylinder whose height is 16 cm and radius is 12 cm, a conical cavity of height 8 cm and of base radius 6 cm is hollowed out Find the volume and total surface area of the remaining solid.
Answer 2
Radius of solid cylinder (R) = 12 cm
and height (H) = 16 cm.
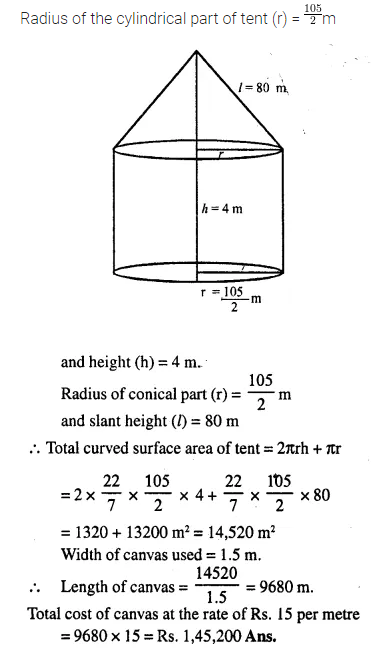
Question 3.
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 80 m, calculate the total area of canvas required. Also, find the total cost of canvas used at Rs. 15 per metre if the width is 1.5 m.
Answer 3
Question 4.
A circus tent is cylindrical to a height of 8 m surmounted by a conical part. If total height of the tent is 13 m and the diameter of its base is 24 m; calculate:
(i) total surface area .of the tent,
(ii) area of canvas, required to make this tent allowing 10% of the canvas used for folds and stitching.
Answer 4
Total height = 13 m
Diameter of base of the tent = 24 m
∴ Radius (r) = = 12 m
Height of cylindrical part h1 = 8 m
and height of conical part (h2) = 13 – 8 = 5 m

Question 5.
A cylindrical boiler, 2 m high, is 3.5 m in diameter. It has a hemi-spherical lid. Find the volume of its interior, including the part covered by the lid.
Answer 5
Diameter of cylinderical boiler = 3.5 m

Question 6
A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylindrical part is 4 m and the diameter of hemisphere is 3.5 m. Calculate the capacity and the internal surface area of the vessel.
Answer 6
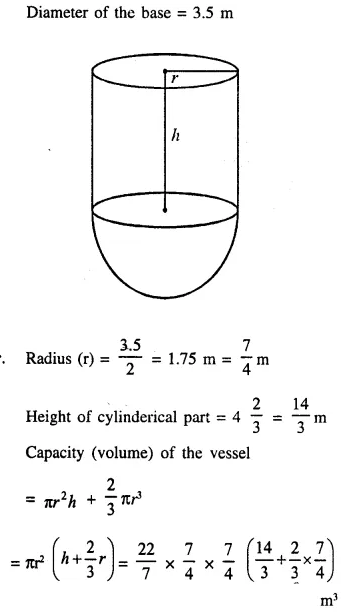

Question 7.
A wooden toy is in the shape of a cone mounted on a cylinder as shown alongside.
If the height of the cone is 24 cm, the total height of the toy is 60 cm and the radius of the base of the cone = twice the radius of the base of the cylinder = 10 cm ; find the total surface area of the toy. [Take π = 3.14]
Answer 7
Height of the conical part (h1)= 24 cm
total height of the toy = 60 cm
∴ Height of cylinderical part (h) = 60-24 = 36 cm
Radius of the cone (r) = twice the radius of the cylinder = 10 cm
∴ Radius of cylinder (r1) = 5 cm

Qustion 8.
A cylindrical container with diameter of base 42 cm contains sufficient water to submerge a rectangular solid of iron with dimensions 22 cm x 14 cm x 10.5 cm. Find the rise in level of the water when the solid is submerged.
Answer 8
Diameter of cylinderical container = 42cm
∴ Radius (r) = = 21 cm.
Dimension of a rectangular solid = 22 cm x 14cm x 10.5 cm
∴ Volume of solid
= 22 x 14 x 10.5 cm3 ….(i)
Let the height of water = h
∴ Volume of water in the container
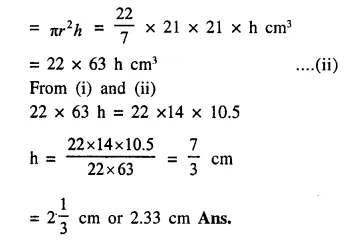
Question 9.
Spherical marbles of diameter 1.4 cm are dropped into beaker containing some water and are fully submerged. The diameter of the beaker is 7 cm. Find how many marbles have been dropped in it if the water rises by 5.6 cm.
Answer 9
Diameter of spherical marble = 1.4 cm.
∴ Radius = = 0.7 cm.
Volume of one ball = πr3

Question 10.
The cross-section of a railway tunnel is a rectangle 6 m broad and 8 m high surmounted by a semi-circle as shown in the figure. The tunnel is 35 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs. 2.25 per m2.
Answer `10
Breadth of’tunnel = 6 m
and height = 8m
Length of tunnel = 35 m
Radius of semicircle = = 3 m.
Circumference of semicircle = πr = x 3 =
m
∴ Internal surface area of the tunnel

Question 11.
The horizontal cross-section of a water tank is in the shape of a rectangle with semi-circle at one end, as shown in the following figure. The water is 2.4 metres deep in the tank. Calculate the volume of water in the tank in gallons.
(Given : 1 gallon = 4.5 litres)
Answer 11
Length = 21m
breadth = 7 m
Depth of water = 2.4 m
∴ Radius of semicircle = m.
Area of the cross section = Area of rectangle + area of semicircle

Question 12.
The given figure shows the cross-section of a water channel consisting of a rectangle and a semi-circle. Assuming that the channel is always full, find the volume of water discharged through it in one minute if water is flowing at the rate of 20 cm per second. Give your answer in cubic metres correct to one place of decimal.
Answer 12
Rate of water flow = 20 cm/sec.
Period = 1 min. = 60 sec.
Radius of semi-circular part (r) = cm
Height of channel (h) = 7 cm
Length of channel = 20 x 60 = 1200 cm

Question 13.Concise Solutions Mensuration Chapter-20
An open cylindrical vessel of internal diameter 7 cm and height 8 cm stands on a horizontal table. Inside this is placed a solid metallic right circular cone, the diameter of whose base is 3 cm and height 8 cm. Find the volume of water required to fill the vessel.
If this cone is replaced by another cone, whose height is 1 cm and the radius of whose base is 2 cm, find the drop in the water level. [1993]
Answer 13
Diameter of cylinder = 7 cm
∴ Radius (R) = cm
Height (h) = 8 cm

Radius of the base of the cone inside (r) = =
cm
∴ Volume of water required to fill the vessel = Volume of open cylinder – Volume of cone

(ii)
Height of another cone (h) = 1 =
cm
and base radius (r) = 2cm
Change in volume = Volume of big cone Volume of small cone
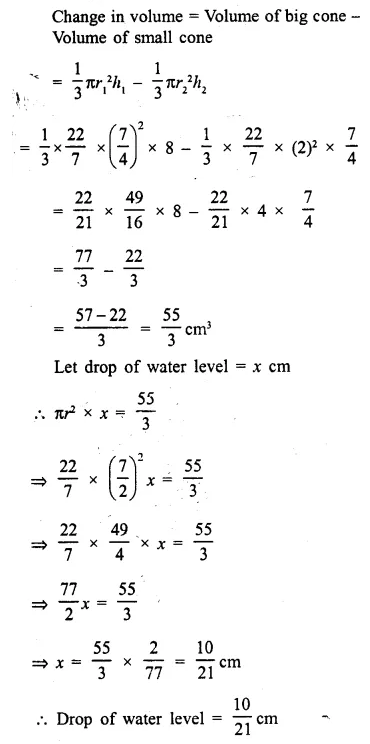
Question 14.
A cylindrical can, whose base is horizontal and of radius 3.5 cm, contains sufficient water so that when a sphere is placed in the can, the water just covers the sphere. Given that the sphere just fits into the can, calculate:
(i)
the total surface area of the can in contact with water when the sphere is in it;
(ii)
the depth of water in the can before the sphere was put into the can. [1997]
Answer 14
Radius of the cylindrical can = 3.5 cm
∴ Radius of the sphere which fits in it
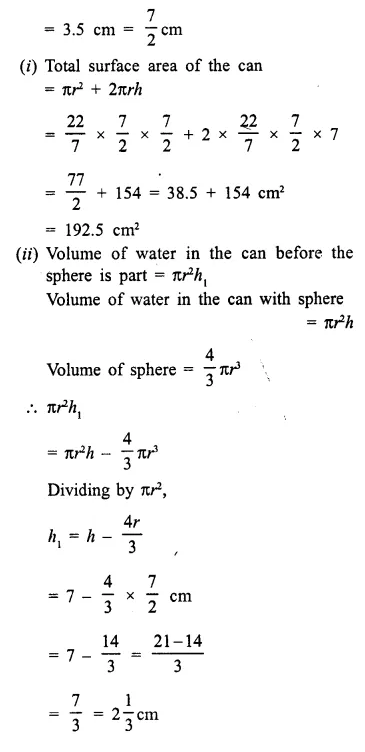
Question 15.
A hollow cylinder has solid hemisphere inward at one end and on the other end it is closed with a flat circular plate. The height of water is 10 cm when flat circular surface is downward. Find the level’of water, when it is inverted upside down, common diameter is 7 cm and height of the cylinder is 20 cm.
Answer 15
(i) Diameter of the cylinder = 7 cm
∴ Radius (r) = cm

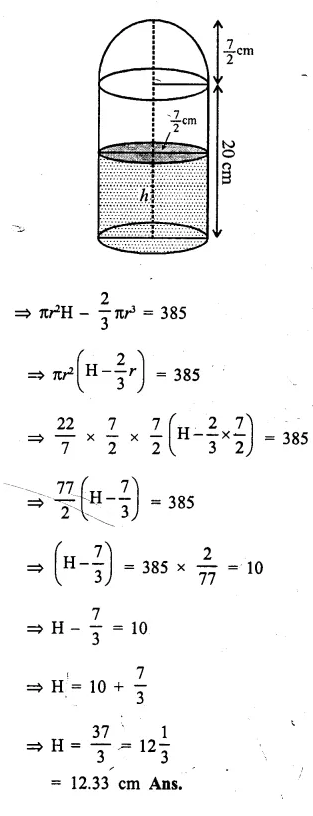
Solutions of Concise Maths Chapter-20 Mensuration EXERCISE – 20 (G)
Question 1.
What is the least number of solid metallic spheres, each of 6 cm diameter, that should be melted and recast to form a solid metal cone whose height is 45 cm and diameter 12 cm ?
Answer 1
Diameter of cone = 12cm
∴ Radius (r1) = = 6cm
Height (A) = 45 cm
∴ Volume = πR2h
= x π x 6 x 6 x 45 cm3
= 540 π cm2
∴ Volume of solid spheres = 540 π cm3
Diameter of one sphere = 6cm
∴ Radius = = 3 cm
∴ Volume of one spherical ball

Question 2.
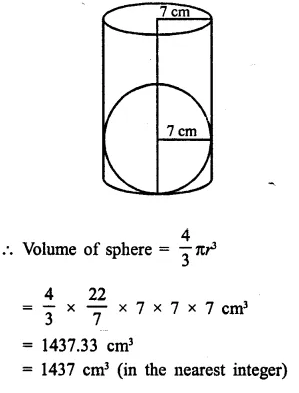
A largest sphere is to be carved out of a right circular cylinder of radius 7 cm and height 14 cm. Find the volume of the sphere. (Answer correct to the nearest integer).
Answer 2
Radius of cylinder = 7 cm
and height 14 cm
By carving a largest sphere from it,
the radius of the sphere will be = 7 cm
Question 3.Concise Solutions Mensuration Chapter-20
A right circular cylinder having diameter 12 cm and height 15 cm is full of ice-cream. The ice-cream is to be filled in identical cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of cones required.
Answer 3
Diameter of cylinder = 12 cm
∴ Radius (r) = = 6 cm
Height (h) = 15 cm
Volume of ice-cream in cylinder = πr²h = π x 6 x 6 x 15 = 540π cm3
∴ Volume of ice-cream = 540π cm3
Now diameter of cone = 6 cm

Question 4.
A solid is in the form of a cone standing on a hemi-sphere with both their radii being equal to 8 cm and the height of cone is equal to its radius. Find, in terms of π , the volume of the solid.
Answer 4
Radius of each cone and hemi-sphere (r) = 8 cm
Height of cone (h) = r = 8 cm
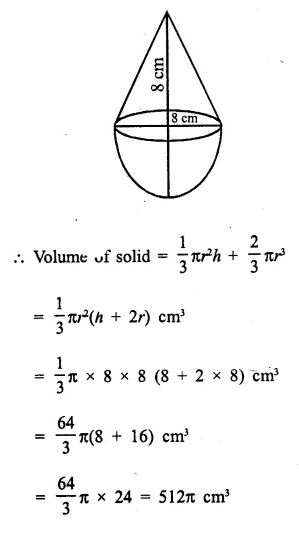
Question 5.
The diameter of sphere is 6 It is melted and drawn into a wire of diameter 0.2 cm. Find the length of the wire.
Answer 5
Diameter of a sphere = 6 cm.
∴ Radius = = 3 cm.

Question 6.
Determine the ratio of the volume of a cube to that of a sphere which will exactly fit inside the cube.
Answer 6
Let edge of the cube = a
∴ Volume of cube = a x a x a = a3
The sphere, which exactly fits in the cube, has radius =
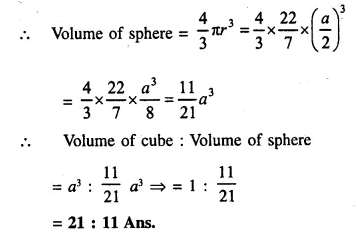
Question 7. Concise Solutions Mensuration Chapter-20
An iron pole consisting of a cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that 1cm3 of iron has 8 gm of mass (approx).
Answer 7
Radius of the base of poles (r) = = 6cm.

P.Q.
When a metal cube is completely submerged in water contained in a cylindrical vessel with diameter 30 cm, the level of water rises by 1 cm. Find:
(i) the length of the edge of the cube.
(ii) the total surface area of the cube.
Answer PQ
Diameter of cylinderical vessel = 30 cm
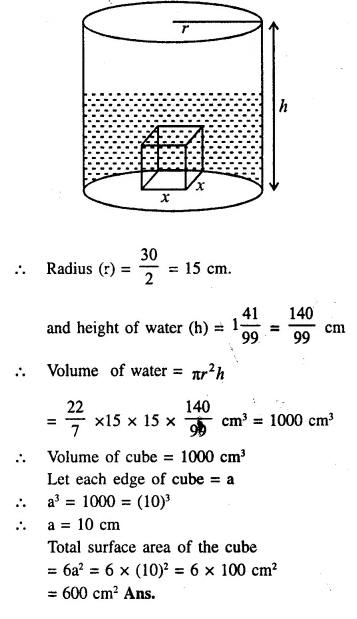
Question 8. Concise Solutions Mensuration Chapter-20
In the following diagram a rectangular platform with a semi-circular end on one side is 22 metres long from one end to the other end. If the length of the half circumference is 11 metres, find the cost of constructing the platform, 1.5 metres high at the rate of Rs. 4 per cubic metres.
Answer 8
Length of platform = 22m
Circumference of semicircle = 11m

Question 9.
The cross-section of a tunnel is a square of side 7 m surmounted by a semi-circle as shown in the following figure. The tunnel is 80 m long. Calculate :
(i) Its volume
(ii) The surface area of the tunnel (excluding the floor) and
(iii) its floor area.
Answer 9
Side of square = 7m
Radius of semicircle = m
Length of tunnel = 80 m.

Question 10.Concise Solutions Mensuration Chapter-20
A cylindrical water tank of diameter 2.8 m and height 4.2 m is being fed by a pipe of diameter 7 cm through which water flows at the rate of 4 ms-1. Calculate, in minutes, the time it takes to fill the tank.
Answer 10
Diameter of cylindrical tank = 2.8 m 2.8
∴ Radius (r) = = 1.4 m
and height (h) = 4.2 m
Volume of water filled in it = πr2h

Question 11.
Water flows, at 9 km per hour, through a cylindrical pipe of cross-sectional area 25 cm2. If this water is collected into a rectangular cistern of dimensions 7.5 m by 5 m by 4 m; calculate the rise in level in the cistern in 1 hour 15 minutes.
Answer 11
Rate of flow of water = 9km / hr
∴ Water flow in 1 hr 15 minutes i.e. in hr

Question 12.
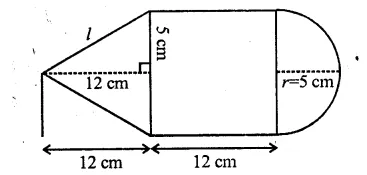
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm, and the other dimensions are as shown. Calculate :
(a) the total surface area,
(b) the total volume of the solid and
(c) the density of the material if its total weight is 1.7 kg.
Answer 12
Diameter = 10 cm
∴ Radius (r) = = 5 cm
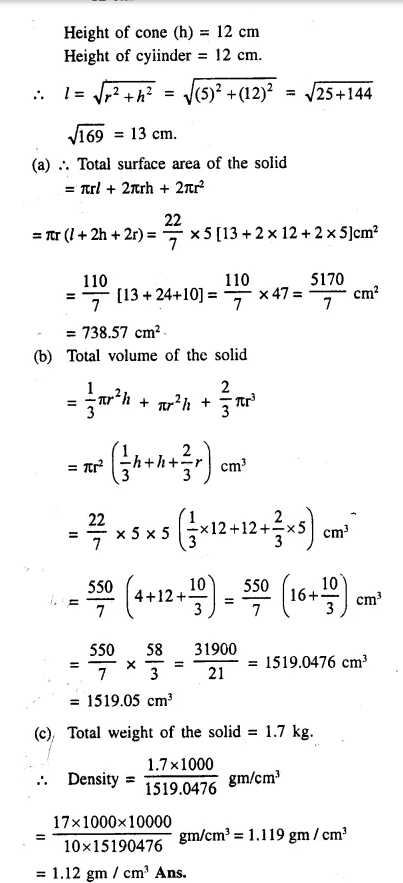
Question 13.
A solid, consisting of a right circular cone, standing on a hemisphere, is placed upright, in a right circular cylinder, full of water, and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm; the radius of the hemisphere is 2 cm and the height of cone is 4 cm. Give your answer to the nearest cubic centimetre. [1998]
Answer 13
Radius of cylinder = 3 cm
and height = 6 cm
Radius of hemisphere = 2 cm
and height of cone = 4 cm
Volume of water in the cylinder when it is full
= πr2h = π x (3)2 x 6 cm3 = 54π cm3
Volume of water displaced = Volume of cone + volume of hemisphere
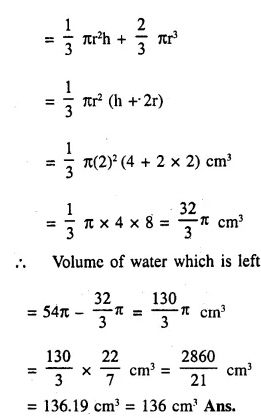
Question 14.
A metal container in the form of a cylinder is surmounted by a hemi-sphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m. Calculate
(i) he total area of the internal surface, excluding the base;
(ii) the internal volume of the container in m3 [1999]
Answer 14
Radius of cylinder = 3.5 m
and height = 7 m.
(i) Total surface area of container excluding the base = curved surface area of cylinder + area of hemisphere = 2πrh + 2πr2

Question 15.Concise Solutions Mensuration Chapter-20
An exhibition tent is in the form of a cylinder surmounted by a cone. The height of the tent above the ground is 85 m and height of the cylindrical part is 50 m. If the diameter of the base is 168 m, find the quantity of canvas required to make the tent. Allow 20% extra for fold and for stitching. Give your answer to the nearest m2. [2001]
Answer 15
Total height of the tent = 85 m.
Daimeter of the base = 168 m.
∴ Radius (r) = = 84 m
Height of cylindrical part = 50 m
Then height of conical part (h) = 85 – 50 = 35 m

P.Q.
The total surface area of a hollow cylinder, which is open from both sides is 3575 cm2; area of the base ring is 357.5 cm2 and height is 14 cm. Find the thickness of the cylinder.
Answer PQ
Total surface area of a hollow cylinder = 3575 cm2
Area of base ring = 357.5 cm2
Height = 14 cm.
Let external radius = R
and internal radius = r
and let thickness of cylinder = (R – r) = d
∴ Total surface area = 2πRh + 2πrh + 2π (R2– r2)
= 2πh (R + r) + 2π (R + r) (R – r)
= 2π (R + r) [h + R – r]
= 2π (R + r) (h + d)
= 2π (R + r) (14 + d)
But 2π (R + r) (14 + d) = 3575 ….(i)
and area of the base = π (R2 – r2) = 357.5
⇒ π (R + r) ( R – r) = 357.5
⇒ π (R + r)d = 357.5 ….(ii)
Dividing (i) by (ii)

Question 16.Concise Solutions Mensuration Chapter-20
A test tube consists of a hemisphere and a cylinder of the same radius. The volume of the water required to fill the whole tube is cm3, and
cm3 of water is required to fill the tube to a level which is 4 cm below the top of the tube. Find the radius of the tube and the length of its cylindrical part.
Answer 16


Question 17.
A solid is in the form of a right circular cone mounted on a hemisphere. The diameter of the base of the cone, which exactly coincides with hemisphere, is 7cm and its height is 8cm. The solid is placed in a cylindrical vessel of internal radius 7 cm and height 10cm. How much water, in cm3, will be required to fill the vessel completely.
Answer 17
Diameter of hemisphere = 7cm
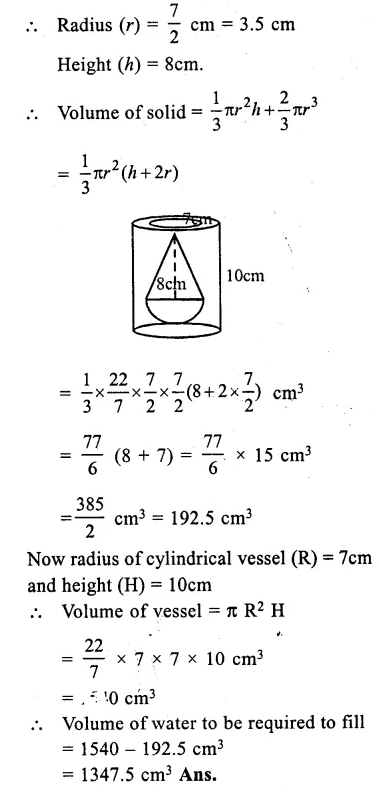
Diameter of the base of a cone = 7cm
∴ Radius (r) = cm = 3.5 cm
Height (h) = 8cm.
Question 18.
Two solid spheres of radii 2 cm and 4 cm are melted and recast into a cone of height 8 cm. Find the radius of the cone so formed. (2015)
Answer 18
Radius of first sphere = 2 cm

Question 19. Concise Solutions Mensuration Chapter-20
A certain number of metallic cones, each of radius 2 cm and height 3 cm are melted and recast into a solid sphere of radius 6 cm. Find the number of cones used. (2016)
Answer 19
Let the number of cones be n,
Let radius of the sphere be rs, radius of a cone be rc and h be the height of the cone.
Volume of sphere = n(Volume of a metallic cone)

Question 20
A conical tent is to accommodate 77 persons. Each person must have 16m3 of air to breathe. Given the radius of the tent as 7m, find the height of the tent and also its curved surface area.
Answer 20
According to the condition in the question,
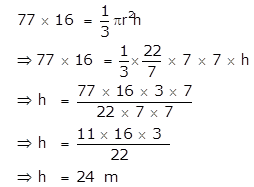
We know that,
l2 = r2 + h2
⇒ l2 = (7)2 + (24)2
⇒ l2 = 49 + 576
and ⇒ l2 = 625
Hence ⇒ l = 25 m
∴ Curved Surface Area = πrl = × 7× 25 = 550m2
Therefore the height of the tent is 24m and it curved surface area is 550m2.
Return to :- Concise Selina Maths Solutions for ICSE Class-10
Thanks
Please share with your friends


