Congruent Triangles ICSE Class-7th Concise Selina Maths

Congruent Triangles ICSE Class-7th Concise Selina mathematics Solutions Chapter-19 Congruency . We provide step by step Solutions of Exercise / lesson-19 Congruency : Congruent Triangles for ICSE Class-7 Concise Selina Mathematics.

Our Solutions contain all type Questions of Exe-19 Congruency to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-7 mathematics .

Congruent Triangles ICSE Class-7th Concise mathematics Selina Solutions Chapter-19 Congruency

Exercise – 19

Question 1.

State, whether the pairs of triangles given in the following figures are congruent or not:

Answer

(i) In these triangles, corresponding sides are not equal.

Hence these are not congruent triangles.

(ii) In the first A,

third angle
= 180° – (40°+ 30°)
= 180° – 70°
= 110°

Hence,

these are congruent triangles
(S.A.S. axiom)

(iii) In these triangles, corresponding two sides are equal but included angles are not-equal.

Hence these are not congruent triangles.

(iv) In these triangles, the corresponding three sides are equal.
Hence, these are congruent triangles.

(v) In these right triangles, one side and diagonal of the one, are equal to the corresponding side and diagonal are equal.

Hence these are congruent triangles.

(vi) In these triangles, two sides and one angle of the one are equal to the corresponding sides and one angle of the other are equal.
Hence these are congruent triangles.

(vii)

In Δ ABC, AB = 2 cm, BC = 3.5 cm and ∠C = 80° and in ∆ DEF, DE = 2 cm, DF = 3.5 cm and ∠D = 80°

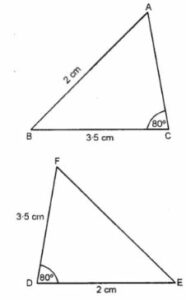
From the figure, we see that two corresponding sides are equal but their included angles are not equal.
Hence, these are not congruent triangles

Question 2.

In the given figure, prove that:
∆ABD ≅ ∆ ACD

Answer

In Δ ABD and Δ ACD,
AD = AD …………..(common)
AB = AC ……………(given)
BD = DC ……………(given)
so Δ ABD ≅ Δ ACD ………….(S.S.S. Axiom)
Hence proved.

Question 3.

Prove that:
(i) ∆ABC ≡∆ADC
(ii) ∠B = ∠D
(iii) AC bisects angle DCB

Answer

Given:

According to the figure,
AB = AD,

CB = CD

To prove: Δ ABC ≅ Δ ADC
∠B = ∠D

AC bisects angle DCB

Proof:

In Δ ABC and Δ ADC,
AC = AC ………….(common)
AB = AD ………….(given)
CB = CD ………….(given)

(i)

∴ Δ ABC ≅ Δ ADC ……………..(SSS aciom)

(ii)

∴ ∠B = D ……………..(c.p.c.t.)
∠BCA = ∠DCA

(iii)

∴ AC bisects ∠DCB

Question 4.

Prove that:
(i) ∆ABD ≡ ∆ACD
(ii) ∠B = ∠C
(iii) ∠ADB = ∠ADC
(iv) ∠ADB = 90°

Answer

Given:

According to the figure,
AD = AC
BD = CD

Proof:

In Δ ABD and Δ ACD
AD = AD ………(common)
AD = AC ……….(given)
BD = CD ………..(given)

(i)

∴ Δ ABD ≅ Δ ACD ……..(SSS axiom)

(ii)

∴ ∠B = ∠C ………….(c.p.c.t.)

(iii)

∠ADB = ∠ADC ……….(c.p.c.t.)

But ∠ADB + ∠ADC = 180° ……….(Linear pair)

∴ ∠ADB = ∠ADC

(iv)

∠ADB = ∠ADC

= 180°/2

= 90°

Question 5.

In the given figure, prove that:
(i) ∆ACB ≅ ∆ECD
(ii) AB = ED

Answer

(i)

Δ ACB and Δ ECD,

AC = CE …………….(given)

∠ACB = ∠DCE …………(vertically opposite angles)

BC = CD ………….(given)

∴ Δ ACB ≅ Δ ECD …………..(S.A.S. Axiom)

(ii)

Hence,

AB = ED …………….(c.p.c.t.)

Hence proved.

Question 6.

Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D

Answer

Proof:

(i)

In ∆ ABC and ∆ ADC

AC = AC ………..(common)

AB = DC …………(given)

BC = AD ………..(given)

∴ ∆ ABC ≅ ∆ ADC …………….(S.S.S. Axiom)

(ii)

Hence,

∠B = ∠D ………..(c.p.c.t.)

Hence proved.

Question 7.

In the given figure, prove that: BD = BC.

Answer

Proof:

right Δ ABD and Δ ABC

Side AB = Side AB ……………….(common)

Hypotenuse AD = Hypotenuse AC ……………(given)

so Δ ABD ≅ Δ ABC …………….(R.H.S. Axiom)

Hence,

BD = BC ……………..(c.p.c.t.)

Hence proved.

Question 8.

In the given figure ;
∠1 = ∠2 and AB = AC. Prove that:
(i) ∠B = ∠C
(ii) BD = DC
(iii) AD is perpendicular to BC.

Answer

Proof:
Δ ADB and Δ ADC,
AB = AC ………(given)
∠1 = ∠2 …………(given)
AD = AD ………….(common)
so Δ ADB ≅ Δ ADC …………….(S.A.S. Axiom)

(i) Hence,

∠B = ∠C …………..(c.p.c.t.)

(ii)

BD = DC ……………(c.p.c.t.)

(iii)

∠ADB = ∠ADC …………(c.p.c.t.)
But ∠ADB + ∠ADC = 180° ….(Linear pair)
∴ ∠ADB = ∠ADC = 90°
Hence,

AD is perpendicular to BC.

Hence proved.

Question 9.

In the given figure prove tlyat:
(i) PQ = RS
(ii) PS = QR

Answer

Proof:
Δ PQR and Δ PSR,
PR = PR ……….(common)
∠PRQ = ∠RPS …………(given)
∠PQR = ∠PSR …….(given)
so Δ PQR ≅ Δ PSR ……………..(A.A.S. Axiom)
Hence,

(i)

PQ = RS ………….(c.p.c.t.)

(ii)

QR = PS ……………(c.p.c.t.)
or PS = QR
Hence proved.

Question 10.

(i) ∆ XYZ ≅ ∆ XPZ
(ii) YZ = PZ
(iii) ∠YXZ = ∠PXZ

Answer

Right Δ XYZ and Δ XPZ,

Side XY = SIde XP …….(given)

Hypotenuse XZ = hypotenuse XZ ………(common)

(i)

so Δ XYZ ≅ Δ XPZ ………..(R.H.S. Axiom)

Hence,

(ii) YZ = PZ ………….(c.p.c.t.)

(iii) ∠YXZ = ∠PXZ ………..(c.p.c.t.)

Hence proved.

Question 11.

In the given figure, prove that:
(i) ∆ABC ≅ ∆ DCB
(ii) AC=DB

Answer

Proof:

Δ ABC and Δ DCB,

CB = CB ………..(common)

∠ABC = ∠BCD ……….(each 90°)

and AB = CD ………….(given)

(i)

∴ Δ ABC ≅ Δ DCB …………..(S.A.S. Axiom)

(ii) Hence,

AC = DB …………(c.p.c.t.)

Hence proved.

Question 12.

In the given figure, prove that:
(i) ∆ AOD ≅ ∆ BOC
(ii) AD = BC
(iii) ∠ADB = ∠ACB
(iv) ∆ADB ≅ ∆BCA

Answer

Proof:

Δ AOD and Δ BOC

OA = OB ……..(given)

∠AOD = ∠BOC ………….(vertically opposite angles)

OD = OC …………(given)

(i)

so Δ AOD ≅ Δ BOC …………….(S.A.S. Axiom)

Hence,

(ii)

AD = BC ……….(c.p.c.t.)

(iii)

∠ADB = ∠ACB …..(c.p.c.t.)

(iv)

Δ ADB ≅ Δ BCA

Δ ADB = Δ BCA …………..(Given)

AB = AB ……………..(Common)

so Δ AOB ≅ Δ BCA

Hence proved.

Question 13.

ABC is an equilateral triangle, AD and BE are perpendiculars to BC and AC respectively. Prove that:
(i) AD = BE
(ii)BD = CE

Answer

Δ ABC,

AB = BC = CA,

AD ⊥ BC,

BE ⊥ AC.

Proof:

Δ ADC and Δ BEC

∠ADC = ∠BEC ………..(each 90°)

∠ACD = ∠BCE …………..(common)

and AC = BC …………(sides of an equilateral triangle)

so Δ ADC ≅ Δ BEC ………..(A.A.S. Axiom)

Hence,

(i) AD = BE ………..(c.p.c.t.)

(ii) BD = CE ………..(c.p.c.t.)

Hence proved.

Question 14.

Use the information given in the following figure to prove triangles ABD and CBD are congruent.
Also, find the values of x and y.

Answer

Given:

According to the figure,
AB = BC,

AD = DC

∠ABD = 50,

∠ADB = y − 7°

∠CBD = x + 5°,

∠CDB = 38°

Find:

The value of x and y

In Δ ABD and Δ CBD

BD = BD ……..(common)

AB = BC ……..(given)

AD = CD ………..(given)

so Δ ABD ≅ Δ CBD ………(SSS axiom)

so ∠ABD = ∠CBD

50 = x + 50°

x = 50° − 5° = 45°

and ∠ADB = ∠CDB

y − 7° = 38°

y = 38° + 7° = 45°

Hence,

x = 45°,

y = 45°

Question 15.

The given figure shows a triangle ABC in which AD is perpendicular to side BC and BD = CD. Prove that:
(i) ∆ABD ≅ ∆ACD
(ii) AB=AC
(iii) ∠B = ∠C

Answer