Conservation of Momentum and Collision Numerical Class 11 Nootan ISC Physics Solutions Ch-9 Work Energy and Power. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-11 Physics.

Conservation of Momentum and Collision Numerical Class 11 Nootan ISC Physics Solutions Ch-9 Work Energy and Power
| Board | ISC |
| Class | 11 |
| Subject | Physics |
| Writer | Kumar and Mittal |
| Publication | Nageen Prakashan |
| Chapter-9 | Work Energy and Power |
| Topics | Numericals on Conservation of Momentum and Collision |
| Academic Session | 2024-2025 |
Numericals on Conservation of Momentum and Collision
Class 11 ISC Nootan Solutions Ch-9 Work Energy and Power of Kumar and Mittal Physics of Nageen Prakashan
Question-29: A block of wood of mass 5 kg is suspended by a thread. A gun is fired in the horizontal direction and the bullet strikes the block and is embedded in it. As a result the block is raised to 15 cm. If the mass of the bullet be 20 g, find the initial velocity of the bullet. (g = 9.8 m/s²)
Answer- According to law of conservation of momentum
momentum before strike = momentum after strike
let velocity of bullet is v then,
0.02 x v + 5 x 0 = ( 5.02 ) V
where V is the velocity after strike
now according to conservation of energy
1/2(5.02) V² = (5.02) x 9.8 x 0.15 (h = 0.15 m)
V = √ 2 x 9.8 x 0.15 = 1.7 m/s
substituting value of V
0.02 x v = 5.02 x 1.7
v ≈ 430 m/s
Question-30: A bullet of mass 0.02 kg moving with a speed of 200 m/s strikes a 2 kg wooden block suspended by a 1 m long thread and is embedded in the block. What is the maximum inclination of the thread with the vertical? (g = 9.8 m/s²)
Answer-
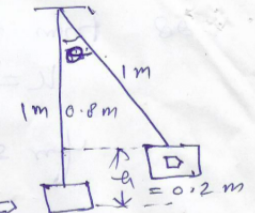
momentum before striking = momentum after striking
=> .02 x 200 +0 = 2.02 x v
v = velocity of block
=> v = 200 x .02 / 2.02 = 1.98 m/s
again 1/2 mv² = m g h
=> h = v²/2g = 1.98 x 1.98 / 2 x 9.8 => 0.2 m
cos θ = 0.8/1 => 4/5
θ = cos^-1(4/5) => 37°
Question-31: A stationary bomb explodes into two fragments of masses 0.4 kg and 4 kg. If the bigger fragment has a kinetic energy of 100 J, find the kinetic energy of the smaller fragment.
Answer- K.E. of bigger fragment = 100 J (let its velocity v)
then 1/2 x 4 x v² = 100
v = √50 = 5√2 m/s
according to law of conservation of momentum
momentum of smaller fragment = momentum of bigger fragment
=> 0.4 x v = 5√2 x 4
=> v = 50√2
∴ its K.E. =1/2 x 0.4 x (50√2)² = 1000 J
Question-32: A neutron (mass 1.67 x 10^-27 kg) moving at a speed of 1.0 x 10^8 m/s collides with a deutron (mass 3.34 x 10^27 kg) at rest and sticks to it. Find the speed of the composite particle triton.
Answer- m1 v1 + m2 v2 = (m1 + m2)v
=> 1.67 x 10^-27 x 1 x 10^8 + 0
=> (1.67 x 10 ^-27 + 3.34 x 10^-27)v
=> v = (1.67 x 10^-27 x 10^8) / (5.01 x 10^-27) = 3.33 x 10^7 m/s
Question-33: A 20 kg, mass which is moving with a speed of 10 m/s strikes a stationary mass of 5 kg. After collision the masses stick together. (a) With what speed does the combined mass move? (b) What was the kinetic energy of the whole system before the collision? (c) What is the kinetic energy after the collision? (d) Where has the remaining energy gone?
Answer- (a) m1 v1 + m2 v2 = (m1 + m2)v
=> 20 x 10 + 5 x 0 = 25 x v
=> v = 200/25 = 8 m/s
(b) K.E. before collision
=> 1/2 m1 v1² + 1/2 m2 v2² (0)
=> 1000 J
(c) K.E. after collision
= 1/2 (m1 +m2) v²
= 1/2 x 25 x 8²
= 800 J
(d) changes to heat
Question-34: A body of mass 2 kg moving with a velocity of 3 m/s collides head-on with a second body of mass 1 kg coming from the opposite direction with a velocity of 4 m/s. After collision, the two bodies stick together. Find the velocity of the sticked bodies.
Answer-

according to law of conservation of momentum
m1 v1 + m2 v2 = (m1 + m2)v
v = m1 v1 + m2 v2 / m1 + m2
=> 2 x 3 + 1(-4) / 2+1 => 2/3 m/s
Question-35: A proton of mass 1.67 x 10^-27 kg collides elastically head-on with an α-particle of mass 6.68 x 10^-27 kg initially at rest. After the collision, the α-particle moves with a speed of 8 x 10^5 m/s. Find the speed the proton before and after the collision.
Answer- Given ;
Two masses 1.67 x 10 kg and 6.68 x 10-2 kg
Thus by conservation of momentum ;
m1 u1+m2 u2 = m1 v1 + m2 v2
Here u2 = 0
m1 u1=m1 v1 + m2 v2 ……(i)
For elastically e = 1
1= v2 – v1 / u1 u2
u1 – u2 = v2 – v1…….(ii)
From (i) and (ii) we get
v1 = 2 m2 u2 / m1 + m2
v2 = (m2 – m1)u2 / m1 + m2
putting given value in formula we get
v1 = 2 x 6.68 x 10^-2 x 8 x 10 / 6.68 x 10^-2 +1.67 x 10
v1 = 0.637 m/sec
v2 =(6.68 x 10^-2 -1.67 × 10)8 × 10 / 6.68 x 10^-2 +1.67 x 10
v2 = -79.36 m/sec
Question-36: A particle of mass 1.8 × 10^-27 kg moving with a speed of 10^6 m/s collides with another particle of mass 3.6 x 10^-27 kg which is initially at rest. The collision is elastic and head-on. Find the speed of each particle after collision.
Answer- m1 = 1.8 x 10^-27 kg u1 = 10^6 m/s
m2 = 3.6 x 10^-27 kg = 2m1 u2 = 0
for perfect elastic collision
=> v1 = (m1 – m2 / m1 + m2) u1 + 2m2 u2 / m1 + m2
=> v1 = (m1 – 2m1 / 3m1) x 10^6 + 0
=> v1 = – 1/3 x 10^6 m/s (rebound)
v2 = (m2 – m1 / m2 + m1)u2 + 2m1 u1 / m2 + m1
=> 0 = 2m1 x 10^6 / 3m1
=> 2/3 x 10^6 m/s (same direction)
Question-37: A ball A of mass 2.4 kg suffers an elastic head-on collision with another ball B at rest. After collision, the ball A continues moving in the same direction with a speed 1/5 of its original speed while the ball B starts moving forward. Find the mass of the ball B.
Answer- m1 = 2.4 kg u1 = u v1 = u/5 u2 = 0 m2=?
According to formula of perfect elastic collision
v1 = (m1 – m2 / m1 + m2) u1 + 2m2 u2 / m1 + m2
=> u/5 = (2.4 – m2 / 2.4 + m2) u
=> 1/5 = 2.4 – m2 / 2.4 + m2
=> 12 – 5m2 = 2.4 + m2
=> 6m2 = 9.6
=> m2 = 1.6 kg
Question-38: A 30 kg mass moving at 18.0 m/s collides with a 90 kg mass moving at 14.4 m/s in the opposite direction. The collision is elastic and head-on. Find the velocity of each mass after the collision.
Answer- v1 = (m1 – m2 / m1 + m2) u1 + 2m2 u2 / m1 + m2
=> (30 – 90 / 120) 18 + 2 x 90 x (- 14.4) / 120
=> (18 x -60 + 2 x 90 x -14.4) / 120 = – 30.6 m/s
again
v2 = (m2 – m1 / m2 + m1)u2 + 2m1 u1 / m2 + m1
=> (90 – 30 / 120) (- 14.4) + (2 x 30 x 18) / 120
=> (60 x -14.4 + 2 x 30 x 18) / 120 = 1.8 m/s
Question-39: A 0.1 kg ball moving at a speed of 10 m/s collides with an identical ball at rest. After collision, the two balls move symmetrically each making an angle of 30° with the original direction of motion of the moving ball. Find the new speed of each ball. Is the collision elastic?
Answer- Initial momentum in horizontal direction = 01 x 10 = 1 kg m s^-1
initial momentum in vertical direction = 0
∴ vertical direction momentum after collision = 0
horizontal momentum after collision = 0.1 v cos 30 x 2 = v √3 x 0.1 kg m s^-1
According to law of conservation of momentum
=> 1 = v √3 x 0.1 = v = 1 / 0.1 x √3 = 10 / √3 = 5.77 m/s
Since initial energy ≠ final energy
∴ collision is non elastic.
Question-40: A 10 kg ball A moving at a speed of 8.0 m/s collides with a 20 kg ball B initially at rest. After collision, the balls A and B move along directions making angles of 30° and 45° respectively with the initial direction of motion of A. Find the final speeds of the balls A and B.
Answer- Mass of ball A = 10 kg , Mass of ball B = 20 kg , Speed of A = 8 m/s
The ball A and B move along direction making angles of 30° and 45°
respectively with the initial direction of mass of A.
We need to calculate the final speed of the balls A and B
Using conservation of momentum
For x-axis,
m1u1+m2u2 = m1v1 +m2v2
Put the value into the formula
10 x 80 + 0 = 10 v1 cos 30+ 20 v2 cos 45
80=5 v1 √3 + 10 v2 √2…(1)
For y-axis,
m1 v1 sin θ = m2 v2 sin Ø
Put the value into the formula
10 v1 sin 30 = 20 v2 sin 45
5 v1 = 10 v2√2….(II)
Form equation (1) and (II)
v1 = 5.85 m/s
v2 = 2.07 m/s
—: end Conservation of Momentum and Collision Numerical Class 11 Nootan ISC Solutions Ch-9 Work Energy and Power :—
Return to : – Nootan Solutions for ISC Physics Class-11 Nageen Prakashan
Thanks
Please Share with your friends if helpful


