Coordinate Geometry Class 10 OP Malhotra Exe-11A ICSE Maths Solutions Ch-11 questions as latest prescribe guideline for upcoming exam. In this article you would learn how to coordinate of point divide two point in certain ration. Visit official Website CISCE for detail information about ICSE Board Class-10 Mathematics.

Coordinate Geometry Class 10 OP Malhotra Exe-11A ICSE Maths Solutions Ch-11
| Board | ICSE |
| Publications | S Chand |
| Subject | Maths |
| Class | 10th |
| Chapter-11 | Coordinate Geometry |
| Writer | OP Malhotra |
| Exe-11A | Division of section formula |
| Edition | 2024-2025 |
Internal Section Formula
Let A(x1, y1) and B(x2, y2) be the endpoints of the given line segment AB and C(x, y) be the point that internally divides AB in the ratio m : n.
x = (mx2 + nx1) / (m + n)
y = (my2 + ny1) / (m + n)
Formula for Midpoint
Let two points A(x1, y1) and B(x2, y2), and a point M(x, y) be the midpoint of the line segment AB
formula for finding the midpoint is x = ((x1 + x2)/2, and y = (y1 + y2)/2)
Centroid Formula
- x1, x2, x3 are the x-coordinates of the vertices of a triangle.
- y1, y2, y3 are the y-coordinates of the vertices of a triangle.
x = [(x1 + x2 + x3) / 3,
y = (y1 + y2 + y3) / 3
Exercise- 11A
Coordinate Geometry Class 10 OP Malhotra Exe-11A ICSE Maths Solutions Ch-11
Que-1: Find the mid-points of lines joining
(a) (5,8), (9,11) (b) (0,0), (8,-5) (c) (-7,0), (0,10) (d) (-4,3), (6,-7)
Sol: Mid-point = [{(x1+x2)/2}, {(y1+y2)/2}]
(a) Mid-point = [{(5+9)/2}, {(8+11)/2}]
= [(14/2), (19/2)]
= [7, 19/2].
(b) Mid-point = [{(0+8)/2}, {(0-5)/2}]
= [(8/2), (-5/2)]
= [4, -5/2].
(c) Mid-point = [{(-7+0)/2}, {(0+10)/2}]
= [(-7/2), (10/2)]
= [-7/2, 5].
(d) Mid-point = [{(-4+6)/2}, {(3-7)/2}]
= [(2/2), (-4/2)]
= [1, -2].
Que-2: Find the mid-point of the sides of a triangle whose vertices are A(1,-1), B(4,-1), C(4,3)
Sol:
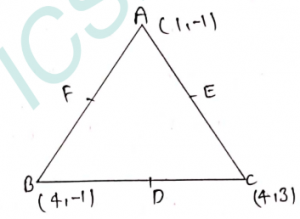
D is the mid-point of BC
Coordinates of D will be
[{(4+4)/2}, {(-1+3)/2}]
= [(8/2), (2/2)] = (4,1).
E is the mid-point of CA
Coordinates of E will be
[{(4+1)/2}, {(3-1)/2}]
= [(5/2), (2/2)] = (5/2, 1).
F is the mid-point of AB
Coordinates of F will be
[{(1+4)/2}, {(-1-1)/2}]
= [(5/2), (-2/2)] = (5/2, -1).
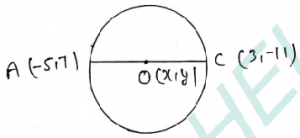
Que-3: Find the centre of a circle if the end points of a diameter are A(-5,7) and C(3,-11).
Sol: Let O be the centre of the circle
O will be the mid-point of the diameter of AC
Coordinates of O will be
= [{(-5+3)/2}, {(7-11)/2}]
= [(-2/2), (-4/2)]
= (-1, -2).
Que-4: If M is the mid-point of AB, find the co-ordinates of :
(a) A if the coordinates of M and B are M(2,8) and B(-4,19) and
(b) B if the coordinates of A and M are A(-1,2) and M(-2,4).
Sol: (a) Mid-point = [{(x1+x2)/2}, {(y1+y2)/2}]
2 = (x1-4)/2, 8 = (y1+19)/2
4 = x1-4, 16 = y1+19
x1 = 8, y1 = -3.
A(8,-3).
(b) Mid-point = [{(x1+x2)/2}, {(y1+y2)/2}]
-2 = (-1+x2)/2, 4 = (2+y2)/2
-4 = -1+x2, 8 = 2+y2
x2 = -3, y2 = 6.
B(-3,6).
Que-5: Find the coordinates of a point which divides internally the join of the points
(a) (8,9) and (-7,4) in the ratio 2:3
(b) (1,-2) and (4,7) in the ratio 1:2
Sol: P = [{(mx2+nx1)/(m+n)}, {(my2+ny1)/(m+n)}]
(a) Given that m : n = 2 : 3 and points are (8, 9) and (-7, 4)
Using equation (1), we get,
P = [{(2×(−7)+3×8)/(2+3)}, {(2×4+3×9)/(2+3)}]
⇒ P = [{(−14+24)/5}, {(8+27)/5}]
⇒ P = (10/5, 35/5)
⇒ P = (2, 7)
(b) Given that m : n = 1 : 2 and points are (1, -2) and (4, 7)
Using equation (1), we get,
P = [{(1×4+2×1)/(1+2)}, {(1×7+2×(-2))/(1+2)}]
⇒ P = [{(4+2)/3}, {(7-4)/3}]
⇒ P = (6/3, 3/3)
⇒ P = (2, 1)
Que-6: Find the coordinates of a points of trisection of the line joining the points (2,3) and (6,5)
Sol: P = [{(mx2+nx1)/(m+n)}, {(my2+ny1)/(m+n)}]
Substitute m = 1 and n = 2
P = [{(1×6+2×2)/(1+2)}, {(1×5+2×3)/(1+2)}]
⇒ P = [{(6+4)/3}, {(5+6)/3}]
⇒ P = (10/3, 11/3)
⇒ P = (10/3, 11/3).
P = [{(mx2+nx1)/(m+n)}, {(my2+ny1)/(m+n)}]
Substitute m = 2 and n = 1
P = [{(2×6+1×2)/(2+1)}, {(2×5+1×3)/(2+1)}]
⇒ P = [{(12+2)/3}, {(10+3)/3}]
⇒ P = (14/3, 13/3)
⇒ P = (14/3, 13/3).
Que-7: In what ratio is the line joining the points
(a) (2,-3) and (5,6) divided by the x-axis
(b) (3,-6) and (-6,8) divided by the y-axis
Sol: (a) Let the line joining points A (2, −3) and B (5, 6) be divided by point P (x, 0) in the ratio k : 1.
y = (ky2+y1)/(k+1)
0 = (k×6+1×(-3))/(k+1)
0 = 6k-3
k = 1/2
Thus, the required ratio is 1 : 2.
(b) Let the line joining points A (3, −6) and B (-6, 8) be divided by point P (0, y) in the ratio k : 1.
y = (kx2+x1)/(k+1)
0 = (k×(-6)+1×3)/(k+1)
0 = -6k+3
k = 1/2
Thus, the required ratio is 1 : 2.
Que-8: Find the centroid of the triangle whose angular points are (-4,6), (2,-2) and (2,5) respectively.
Sol: Centroid = (x1+x2+x3)/3 and y = (y1+y2+y3)/3
= (-4+2+2)/3 and (6-2+5)/3
= (0/3) and (9/3)
= (0, 3).
Que-9: If (x1,y1) = (2,3) ; x2 = 3 and y3 = -2 and G is (0,0), find y2 and x3.
Sol: The centroid of a triangle with vertices (x1,y1)(x2,y2)(x3,y3) is given by :
G = (x1+x2+x3)/3 and y = (y1+y2+y3)/3
G (0,0)
0 = x1+x2+x3 and 0 = y1+y2+y3
Substitute the known values
2+3+x3 = 0 and 3+y2-2 = 0
x3 = -5 and y2 = -1.
Que-10: The mid-points of the sides of a triangle are at (1,4), (4,8) and (5,6). Find the coordinates of the vertices of the triangle.
Sol: Let, ABC be a triangle with vertices A(x1,y1), B(x2,y2), C(x3,y3) and P(1,4), Q(4,8), R(5,6) be the midpoints of AB, BC, CA respectively.
Then,
1 = (x1+x2)/2 ⇒ x1+x2 = 2 ⟶ (1)
4 = (y1+y2)/2 ⇒ (y1+y2) = 8⟶(2)
4 = (x2+x3)/2 ⇒ (x2+x3) = 8⟶(3)
8 = (y2+y3)/2 ⇒ (y2+y3) = 16⟶(4)
5 = (x3+x1)/2 ⇒ (x3+x1) = 10⟶(5)
6 = (y3+y1)/2 ⇒ (y3+y1) = 12⟶(6)
Adding equations (1),(3) and (5) we get,
2(x1+x2+x3) = 20 ⇒ x1+x2+x3 = 10⟶(7)
Subtracting equation (7) from (1) ⇒ x3 = 8
Subtracting equation (7) from (3) ⇒ x1 = 2
Subtracting equation (7) from (5) ⇒ x2 = 0
Now, adding equations (2),(4) and (6) we get,
2(y1+y2+y3) = 36 ⇒ y1+y2+y3 = 18⟶(8)
Subtracting equation (8) from (2) ⇒ y3 = 10
Subtracting equation (8) from (4) ⇒ y1 = 2
Subtracting equation (8) from (6) ⇒ y2 = 6
∴ the required coordinates of the vertices of the triangle are
A = (2,2), B = (0,6), C = (8,10).
Que-11: The vertices of a triangle are A(-2,2), B(4,4) and C(8,2). Find the length of the medians to the sides (i) AB, (ii) AC (iii) BC
Sol: The vertices of a triangle are A(-2,2), B(4,4) and C(8,2)
Mid-point of BC
Midpoint = [{(xB+xC)/2}, {(yB+yC)/2}] = [{(4+8)/2}, {(4+2)/2}] = (6,3)
Mid-point of AC
Midpoint = [{(xA+xC)/2}, {(yA+yC)/2}] = [{(-2+8)/2}, {(2+2)/2}] = (3,2)
Mid-point of AB
Midpoint = [{(xA+xB)/2}, {(yA+yB)/2}] = [{(-2+4)/2}, {(2+4)/2}] = (1,3)
Distance = √{(x2-x1)²+(y2-y1)²}
(i) Length of AB
= √{(8-1)²+(2-3)²} = √(7²+(-1)²)
= √49+1 = √50
= 5√2.
(ii) Length of AC
= √{(4-3)²+(4-2)²} = √(1²+2²)
= √1+4
= √5.
(iii) Length of BC
= √{(6-(-2))²+(3-2)²} = √(8²+1²)
= √64+1
= √65.
Que-12: Calculate the coordinates of the point P which divides the line joining A(-1,3), B(5,9) in the ratio 1 : 2.
Sol: Let the co-ordinates of the point P be (x, y)
x = [{(m1x2+m2x1)/(m1+m2)}]
= [{1×5+2×(-1))/(1+2)}]
= 3/3 = 1
y = {(m1y2+m2y1)/(m1+m2)}
= {(1×9+2×3)/(1+2)}
= 15/3
= 5
Thus, the co-ordinates of point P are (1,5)
Que-13: The mid-point of the line joining A(2,p) and B(q,4) is (3,5). Calculate the numerical value of p and q.
Sol: Given, (3, 5) is the mid-point of A(2, p) and B(q, 4).
By mid-point formula,
⇒ 3 = {(2+q)/2} and 5 = {(p+4)/2}
⇒ 2+q = 6 and p+4 = 10
⇒ q = 4 and p = 6
Hence, p = 6 and q = 4.
Que-14: (a) A is the mid-point on y-axis whose ordinate is 5 and B is the point (-3,1). Calculate the length of AB.
(b) The mid-point of the line joining (a,2) and (3,6) is (2,b). Find the numerical value of a and b.
Sol: (a) Distance formula: The distance between points (x1,y1) and (x2,y2) is given by √{(x2−x1)²+(y2−y1)²}
Since, A is a point on y−axis => absisca = 0 and ordinate is 5 => A(0,5) & B(−3,1)
AB = √{(3)²+(4)²}
AB = √(9+16)
AB = √25 = 5cm.
(b) AC : CB = 1 : 1
Coordinates of C are ,
C (2 , b) = C {(a+3)/2}, {(2+6)/2}
2 = (a+3)/2 , b = 4
4 = a + 3 , b = 4
a = 1 , b = 4
Que-15: The line joining A(2,3) and B(6,-5) meets the x-axis at P. Write down the y-coordination of P. Hence find the ratio of AP : PB.
Sol: Since, point K lies on x-axis, its ordinate is 0.
Let the point K (x, 0) divides AB in the ratio k : 1.
We have,
y = {(k×(-5)+1×3)/(k+1)}
0 = {(-5k+3)/(k+1)
k = 3/5
Thus, K divides AB in the ratio 3 : 5.
Que-16: In the given figure P(2,3) is the mid-point of the line AB. Write down the coordinates of A and B.
Sol: Let coordinate of A is ( A , 0)
and of B is ( 0 , B )
Because P is the midpoint of AB Then,,
( A + 0)/2 = 2
A = 4 &
( 0 + B )/2 = 3
B = 6
Hence coordinates of points A & B is ( 4 , 0 ) & ( 0 , 6 ) respectively.
Que-17: The line segment joining A(2,3) and B(6,-5) is intersected by the x-axis at a point K. Write down the ordinate of the point K. Find the ratio in which K divides AB.
Sol: Since, point K lies on x-axis, its ordinate is 0.
Let the point K (x, 0) divides AB in the ratio k : 1.
We have,
y = {(k×(-5)+1×3)/(k+1)}
0 = {(-5k+3)/(k+1)
k = 3/5
Thus, K divides AB in the ratio 3 : 5.
Que-18: (a) Coordinates of A and B are (-3,a) and (1,a+4). The mid-point of AB is (-1,1). Find the value of a.
(b) Calculate the ratio in which the line segment joining (3,4) and (-2,1) is divided by the y-axis.
Sol: (a) Coordinates of A and B are (-3,a) and (1,a+4)
Mid-point is (-1,1)
= (-3+1)/2 and 1 = (a+a+4)/2
= -2/2 and 2 = 2a+4
2a = 2-4
a = -2/2 = -1.
(b) Let A(3,4) and B(−2,1) be the two points
Taking the ratio as k:1 in which the point P divides, we have the co-ordinates to be [{(kx2+x1)/(k+1)}, {(ky2+y1)/(k+1)}]
According to coordinates , point A is 3 units from the y-axis in the positive direction. Similarly point B is 2 units from the y-axis in the negative direction.
[{(k(−2)+3)/(k+1)}, {(k(1)+(4))/(k+1)}] = (0,y)
On solving we get k = 3/2
∴ y-axis divides the line AB in the ratio 3:2
∴ Ratio = 3 : 2
Que-19: (a) P divides the distance between A(-2,1) and B(1,4) in the ratio 2 : 1. Calculate the coordinates of the point P.
(b) Prove that the points A(-5,4), B(-1,-2) and C(5,2) are the vertices of an isosceles right-angled triangle. Find the coordination of D, so that ABCD is a square.
Sol: (a) Let (x, y) be the coordinates of the point P which divides the line segment joining A(-2, 1) and B(1, 4) in the ratio 2 : 1.
∴ Coordinates of P are [{(m1x2+m2x1)/(m1+m2)}, {(m1y2+m2y1)/(m1+m2)}].
Putting the values from question in above formula we get,
⇒ [{(2×1+1×(−2))/(2+1)}, {(2×4+1×1)/(2+1)}]
= [{(2−2)/3}, {(8+1)/3}]
= (0,3).
(b) We have:
AB = √{(-1+5)²+(-2-4)²}
= √(16+36)
= √52
BC = √{(-1+5)²+(-2-2)²}
= √(36+16)
= √52
AC = √{(5+5)²+(2-4)²}
= √(100+4)
= √104
AB2 + BC2 = 52 + 52 = 104
AC2 = 104
∵ AB = BC and AB2 + BC2 = AC2
∵ ABC is an isosceles right-angled triangle.
Let the coordinates of D be (x, y).
If ABCD is a square, then,
Mid-point of AC = Mid-point of BD
{(-5+5)/2}, {(4+2)/2} = {(x-1)/2}, {(y-2)/2}
0 = {(x-1)/2}, 3 = {(y-2)/2}
x = 1, y = 8
Thus, the co-ordinates of point D are (1, 8).
Que-20: A(2,2), B(-2,4), C(2,6) are the vertices of a triangle ABC. Prove that ABC is an isosceles triangle.
Sol: AB = √{(2+2)²+(5-4)²} = √(16+1) = √17 units
BC = √{(-2+2)²+(4-6)²} = √(0+4) = 2 units
AC = √{(2+2)²+(5-6)²} = √(16+1) = √17 units
It can be seen that AB = AC
Hence , the given coordinates are the vertices of an isosceles triangle.
–: End of Coordinate Geometry Class 10 OP Malhotra Exe-11A ICSE Maths Solutions :–
Return to : OP Malhotra S Chand Solutions for ICSE Class-10 Maths
Thanks
Please Share with Your Friends


