Coordinate Geometry Class 10 OP Malhotra Exe-11C ICSE Maths Solutions Ch-11 questions as latest prescribe guideline for upcoming exam. In this article you would learn how to find slope intercept form of a straight line. Visit official Website CISCE for detail information about ICSE Board Class-10 Mathematics.
Coordinate Geometry Class 10 OP Malhotra Exe-11C ICSE Maths Solutions Ch-11
| Board | ICSE |
| Publications | S Chand |
| Subject | Maths |
| Class | 10th |
| Chapter-11 | Coordinate Geometry |
| Writer | OP Malhotra |
| Exe-11C | slope intercept form of a straight line |
| Edition | 2024-2025 |
Slope Intercept Form of a Straight Line
The slope-intercept form of a straight line is y=mx + C , where: M is the slope of the line, also known as the gradient and C is y-intercept, or the point where the line crosses the y-axis .
Note: The value of c can be positive or negative based on the intercept is made on the positive or negative side of the y-axis, respectively.
Exercise- 11C
( Coordinate Geometry Class 10 OP Malhotra Exe-11C ICSE Maths Solutions )
Que-1: State the slope of the line (i) 3x+4y = 9 (ii) 3x+2y = 4
Sol: (i) 3x+4y = 9
4y = 9-3x
y = -3x/4 + 9/4
which is in the form as y = mx+c
so, slope m = -3/4.
(ii) 3x+2y = 4
2y = 4-3x
y = -3x/2 + 4/2
which is in the form as y = mx+c
so, slope m = -3/2.
Que-2: Given 3x+2y+4 = 0,
(i) Express the equation in the form y = mx+c.
(ii) Find the slope and the the y-intercept of the line 3x+2y+4 = 0
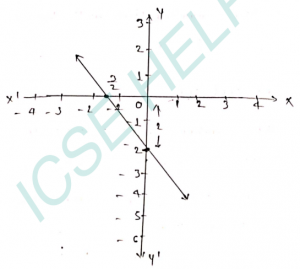
(iii) Use your answer to (ii) above and on a graph paper draw the graph of the straight line 3x+2y+4 = 0.
Sol: (i) 3x+2y+4 = 0
3x+2y = -4
2y = -3x-4
y = -3x/2 – 4/2
which is the form of y = mx+c
(ii) slope (m) = -3/2 and y-intersect (c) = -2.
(iii) The line has been drawn on the graph paper as given here.
Que-3: State the equation of the line which has the y-intercept (a) 2 and a slope 7 (b) -3 and a slope -4 (c) -1 and is parallel to y = 5x-7 (d) 2 and is inclined at 45° to the x-axis (e) -5 and is equally inclined to the axis.
Sol: (a) c = 2 and m = 7
So, equation of the line will be
y = 7x+2
7x-y+2 = 0.
(b) c = -3 and m = -4
So, equation of the line will be
y = -4x-3
4x+y+3 = 0.
(c) c = -1
The line is parallel to the line y = 5x-7 then slope m = 7.
So, the required will be
y = 5x-1.
(d) c = 2
So, the equation inclined at 45° to the x-axis
So, slope (m) = tan Θ = tan 45° = 1
So, the equation at required line will be
y = x+2
x-y+2 = 0.
(e) c = -5
If the line is equally inclined to the x-axis
So, Slope (m) = tan Θ = ±1So, the equation at the line will be
y = x-5
x-y = 5.
Que-4: What will be the value of m and c if the straight line y = mx+c passes through the points (3,-4) and (1,-2) ?
Sol: by the equation of the straight line passing through two points is
(y−y1) = {(y2−y1)/(x2−x1)} (x−x1)
Here the points are
(3,−4),(−1,2)
Then,
{(y−(−4))/(2−(−4))} = {(x−3)/(−1−3)}
(y+4)/6 = (x−3)/−4
-4(y+4) = 6(x-3)
-4y-16 = 6x-18
-4y = 6x-2
y = -(3/2)x+(1/2)
Therefor by comparing this with y=mx+c we get,
m = -(3/2)
c = (1/2).
Que-5: The graph of the equation y = mx+c passes through the points (1,4) and (-2,-5). Determine the values of m and c.
Sol: Since, (1, 4) and (-2, -5) lie on y = mx + c hence, the points must satisfy the equation.
Putting (1, 4) in the equation,
⇒ 4 = m(1) + c
⇒ 4 = m + c
⇒ m = 4 – c (Eq 1)
Putting (-2, -5) in the equation,
⇒ -5 = m(-2) + c
⇒ -5 = -2m + c.
Putting value of m from Eq 1 in above equation,
⇒ -5 = -2(4 – c) + c
⇒ -5 = -8 + 2c + c
⇒ -5 + 8 = 3c
⇒ 3 = 3c
⇒ c = 1.
Putting value of c in Eq 1,
⇒ m = 4 – 1
⇒ m = 3.
Hence, the value of m = 3 and c = 1.
Que-6: Find the equation of the straight line through the given point P and having the given slope m if (a) P(-4,7) ; m = -√3; (b) P(-1,-5); m = -6/11
Sol: (a) The equation as the line will be
y-y1 = m(x-x1)
Hence it passes through P(-4,7) and m = -√3
y-7 = -√3 (x-(-4))
y-7 = -√3x-4√3
√3x+y = 7-4√3.
(b) The line passes through the point P(-1,-5) and has slope (m) = -6/11
So, equation as the line will be
y-y1 = m(x-x1)
y+5 = (-6/11) (x+1)
11y+55 = -6x-6
6x+11y+55+6 = 0
6x+11y+61 = 0.
Que-7: Find the equation to the straight line passes through (a) the origin and perpendicular to x+2y = 4 (b) the point (4,3) and parallel to 3x+4y = 12 (c) the point (4,5) and (i) parallel to, (ii) perpendicular to 3x-2y+5 = 0
Sol: (a) x+2y = 4
2y = -x+4
y = -x/2 + 2
slope (m1) = -1/2
and slope line perpendicular to it (-1/m) = 2.
If the required equation passes through the origin is (0,0)
So, the equation as the line will be
y-y1 = m(x-x1)
y-0 = 2(x-0)
y = 2x
2x-y = 0
(b) 3x+4y = 12
4y = -3x+12
y = -3x/4 + 3
slope (m1) = -3/4
and slope line parallel to it = -3/4.
If the required equation passes through the point is (4,3)
So, the equation as the line will be
y-y1 = m(x-x1)
y-3 = (-3/4)(x-4)
4y-12 = -3x+12
3x+4y = 12+12
3x+4y – 24 = 0.
(c) 3x-2y+5 = 0
2y = 3x+5
y = 3x/2 + 5/2
slope (m1) = 3/2
(i) slope line parallel to it = 3/2.
If the required equation passes through the point is (4,5)
So, the equation as the line will be
y-y1 = m(x-x1)
y-5 = (3/2)(x-4)
2y-10 = 3x-12
3x-2y = 10-12
3x-2y-2 = 0.
(ii) slope line perpendicular to it (-1/m) = -2/3.
If the required equation passes through the origin is (4,5)
So, the equation as the line will be
y-y1 = m(x-x1)
y-5 = (-2/3)(x-4)
3y-15 = -2x+8
2x+3y-15-8 = 0
2x+3y-23 = 0.
Que-8: Find the equations of the line joining the points (a) A(1,1) and B(2,3) (b) P(3,3) and Q(7,6) (c) L(a,b) and M(b,a)
Sol: (a) The equation between two points is
y-y1 = {(y2-y1)/(x2-x1)} (x-x1)
Points are A(1,1) and B(2,3)
y-1 = {(3-1)/(2-1)} (x-1)
y-1 = 2(x-1)
y-1 = 2x-2
2x-y-1 = 0.
(b) The equation between two points is
y-y1 = {(y2-y1)/(x2-x1)} (x-x1)
Points are P(3,3) and Q(7,6)
y-3 = {(6-3)/(7-3)} (x-3)
y-3 = (3/4) (x-3)
4y-12 = 3x-9
3x-4y+3 = 0.
(c) The equation between two points is
y-y1 = {(y2-y1)/(x2-x1)} (x-x1)
Points are L(a,b) and M(b,a)
y-b = {(a-b)/(b-a)} (x-a)
y-b = -1 (x-a)
y-b = -x+a
x+y = a+b.
Que-9: The line represented by 3x+4y = 8 and px+2y = 7 are parallel. Find the value of p.
Sol: Slope of line 3x+4y = 8
= 4y = -3x+8
= y = -3x/4 + 2
m1 = -3/4
Slope of line px+2y = 7
= 2y = -px+7
= y = -px/2 + 7/2
m2 = -p/2
If the lines are parallel then the slope are equal
m1 = m2
-3/4 = -p/2
p = (3×2)/4
p = 3/2.
Que-10: The coordinates of two points E and F are (0,4) and (3,7) respectively. Find : (i) the gradient of EF (ii) the equation of EF (iii) the coordinates of a point where the line EF intersects the x-axis.
Sol: coordinates of two points E and F are (0,4) and (3,7)
(i) slope (m) = (y2-y1)/(x2-x1)
m = (7-4)/(3-0) = 3/3 = 1
gradient = 1.
(ii) the equation of EF =
Y−7 = 1(x−3)
Y−7 = x−3
x−y+4 = 0
(iii) the coordinates of point where EF intersects the x-axis
Y = 0
∴ x+4 = 0
⇒ x = −4
coordinates are (−4,0)
Que-11: P, Q, R have coordinates (-2,1), (2,2) and (6,-2) respectively. Write down : (i) the gradient of QR (ii) the equation of the line through P perpendicular to QR
Sol: (i) Gradient of QR (m) = (y2-y1)/(x2-x1)
m = (-2-2)/(6-2) = -4/4 = -1
gradient = -1.
(ii) the equation of P =
Y−1 = 1(x+2)
Y−1 = x+2
x-y+3 = 0.
Que-12: A line 3x-4y+12 = 0 meets the x-axis at the point P. Find the equation of the line through P, perpendicular to the line 3x+5y-15 = 0.
Sol: A line 3x-4y+12 = 0 meets the x-axis at the point P
So, y-coordinate of P will be 0.
Let the coordinates of P will be (x,0)
If it lies on 3x-4y+12 = 0
So, it satisfy the equation
3x-4(0)+12 = 0
3x+12 = 0
3x = -12
x = –4
So, the coordinate will be (-4,0)
Now, slope of the line 3x+5y-15 = 0
5y = -3x+15
y = (-3x/5) + 3
m = -3/5
So, the slope as the line perpendicular to this line (-1/m)
= -{1/(-3/5) } = 5/3
So, the equation of the perpendicular line through P will be
y-y1 = m (x-x1)
y-0 = (5/3) (x+4)
3y = 5x+20
5x-3y+20 = 0.
Que-13: The line segment joining P(5,-2) and Q(9,6) is divided in the ratio 3:1 by a point A on it. Find the equation of a line through the point A perpendicular to the line x-3y+4 = 0.
Sol: The line segment joining P(5,-2) and Q(9,6) is divided in the ratio 3 : 1
Now, coordinate of A will be
[{(mx2+nx1)/(m+n)}, {(my2+ny1)/(m+n)}]
[{(3×9+1×5)/(3+1)}, {(3×6+1×(-2))/(3+1)}]
[{(27+5)/4}, {(18-2)/4}]
[(32/4), (16/4)] = (8,4)
Slope of the line x-3y+4 = 0
3y = x+4
y = (x/3) + (4/3)
m = 1/3
So, slope of the line perpendicular to it is -1/m
= -{1/(1/3)} = -3.
So, equation of the line through A will be
y-y1 = m (x-x1)
y-4 = -3 (x-8)
y-4 = -3x+24
3x+y-4-24 = 0
3x+y-28 = 0
Que-14: Write down the equation of the line parallel to x-2y+8 = 0 passing the point (1,2).
Sol: The equation of the given line is given by y = mx+c
The given equation is x-2y+8 = 0
⇒y = (x/2) + 4
Comparing the above equation with y = mx+c
We get: m =1/2 (where ‘m’ is the slope of the given line)
Since the given and the required lines are parallel, their slopes will be equal.
Thus, the slope of the required line m = 1/2
The required line passes through the point (1,2)
Let x1 = 1 and y1 = 2
Using the slope-point form, the equation of a line is given by:
y-y1 = m (x-x1)
Substituting the values above, we get:
y-2 = (1/2) (x-1)
⇒ 2y-4 = x-1
⇒ x-2y-1+4 = 0
⇒ x-2y+3 = 0
Hence, the equation of the required line is x-2y+3 = 0.
Que-15: Write down the gradient and intercept on the y-axis of the line (x/3)+(y/4) = 1.
Sol: The equation of the line is given (x/3)+(y/4) = 1.
4x+3y = 12
3y = -4x+12
y = (-4x/3) + 4
gradient (m) = -4/3
y-intercept (c) = 4.
Que-16: (i) Lines 2x-by+5 = 0 and ax+3y = 2 are parallel. Find the relation connecting a and b. (ii) Find the equation of the line through (1,3) making an intercept of 5 on the y-axis.
Sol: (i) 2x – by + 5 = 0
by = 2x + 5
y = (2x/b) + (5/b)
Slope of this line = 2/b
ax + 3y = 2
3y = −ax + 2
y = (-ax/3) + (2/3)
Slope of this line = -a/3
Since, the lines are parallel, so the slopes of the two lines are equal.
∴ 2/b = -a/3
ab = −6.
(ii) Since, y-intercept = 5, so the corresponding point on y-axis is (0, 5).
The line passes through (1, 3).
∴ Slope of the line = (5-3)/(0-1) = 2/(-1) = -2
Required equation of the line is given by:
y − y1 = m(x − x1)
y − 5 = −2(x − 0)
y − 5 = −2x
2x + y = 5.
Que-17: (i) Find the value of p, given that the line (y/2) = x-p passes through the point (-4,4). (ii) Given that the line (y/2) = x-p and the line ax+5 = 3y are parallel, find the value of a.
Sol: (i) The line (y/2) = x – p
and it passes through the point (-4,4)
Hence, it satisfy the line equation
So, 4/2 = (-4) – p
2 = -4-p
p = -4-2
p = -6.
(ii) In equation y/2 = x – p
y = 2x – 2p
m1 = 2
and in equation ax+5 = 3y
y = (ax/3) + (5/3)
m2 = a/3
If these two lines are parallel
Then m1 = m2
2 = a/3
a = 6.
Que-18: A line intersects x-axis at (-2,0) and cuts off an intercept of 3 from the positive side of y-axis. Write the equation of the line.
Sol: Let line intersects x-axis at P(−2, 0) and cuts off an intercept of 3 units at Q.
∴ Co-ordinates of Q are (0, 3)
Now, slope of line PQ
m = (y2-y1)/(x2-x1)
= (0-3)/(-2-0)
= -3/-2
= 3/2
∴ Equation of line PQ will be
y − y1 = m(x − x1)
⇒ y-3 = (3/2) (x-0)
⇒ y-3 = (3/2) x
⇒ 2y – 6 = 3x
⇒ 2y = 3x + 6.
Que-19: (a) In the following figure , write down (i) the coordinates of the points A, B and C; (ii) the equation of the line through A, parallel to BC.
(b) In what ratio is the join of A(0,3) and B(4,1) divided by the x-axis? (AB produces if necessary). Write the coordinates of the point where AB intersects the x-axis.
Sol: (a) (i) The co-ordinates of points A, B and C are (2, 3), (−1, 2) and (3, 0) respectively.
(ii) Slope of BC = (0-2))/(3+1) = -2/4 = -1/2
Slope of a line parallel to BC = Slope of BC = -1/2
Required equation of a line passing through A and parallel to BC is given by
y − y1 = m(x − x1)
y−3 = (-1/2) (x−2)
2y − 6 = −x + 2
x + 2y = 8.
(b) Let the ratio be m1 : m2 when the x-axis intersects the line AB at P.
x = (m1x2+m2x1)/(m1+m2), y = (m1y2+m2y1)/(m1+m2)
x = (m1×4+m2×0)/(m1+m2), y = (m1(1)+m2×3)/(m1+m2)
x = (4m1)/(m1+m2), y = (m1+3m2)/(m1+m2)
∵ P lies on x-axis,
∴ y = 0
∴ (m1+3m2)/(m1+m2) = 0
⇒ m1 + 3m2 = 0
⇒ m1 = -3m2
⇒ m1/m2 = -3/1
⇒ m1 : m2 = -3 : 1
Now, x = (4×(-3))/((-3)+1)
= -12/-2
= 6
∴ Required co-ordinates of P will be (6, 0)
Que-20: Write down the equation of the line AB, through (3,2), perpendicular to the line 2y = 3x+5. AB meets the x-axis at A and y-axis at B. Write down the coordinates of A and B. Calculate the area of ΔOAB where O is the origin.
Sol: 2y = 3x + 5
⇒ y = (3x/2) + (5/2)
Slope of this line = 3/2
Slope of the line AB = -1/(3/2) = -2/3
(x1, y1) = (3, 2)
The required equation of the line AB is
y − y1 = m(x − x1)
y-2 = (-2/3) (x-3)
3y − 6 = −2x + 6
2x + 3y = 12
For the point A (the point on x-axis), the value of y = 0.
2x + 3y = 12
⇒ 2x = 12
⇒ x = 6
Co-ordinates of point A are (6, 0).
For the point B (the point on y-axis), the value of x = 0.
2x + 3y = 12
⇒ 3y = 12
⇒ y = 4
Co-ordinates of point B are (0, 4).
Area of ΔOAB = (1/2)×OA×OB
= (1/2)×6×4
= 12 sq units
Que-21: (i) Write down the coordinates of the point P that divides the line joining A(-4,1) and B(17,10) in the ratio 1:2. (ii) Calculate the distance OP, where O is the origin. (iii) In what ratio does the y-axis divide the line AB?
Sol: (i) Co-ordinates of point P are
[{(1×17+2×(-4))/(1+2)}, {(1×10+2×1)/(1+2)}]
= [{(17-8)/3}, {(10+2)/3}]
= (9/3, 12/3)
= (3, 4)
(ii) OP = √{(0-3)²+(0-4)²}
OP = √(9+16)
OP = √25
OP = 5 units
(iii) Let AB be divided by the point P(0, y) lying on y-axis in the ratio k : 1
∴ (0,y) = [{(k×17+1×(-4))/(k+1)}, {(k×10+1×1)/(k+1)}]
⇒ (0,y) = [{(17k-4)/(k+1)}, {(10k+1)/(k+1)}]
⇒ 0 = (17k-4)/(k+1)
⇒ 17k-4 = 0
⇒ k = 4/17
Thus, the ratio in which the y-axis divide the line AB is 4 : 17.
–: End of Coordinate Geometry Class 10 OP Malhotra Exe-11C ICSE Maths Solutions Ch-11 :–
Return to : OP Malhotra S Chand Solutions for ICSE Class-10 Maths
Thanks
Please Share with Your Friends


