Cubes and Cube-Roots ICSE Class-8th Concise Mathematics Selina Solutions Chapter-4. We provide step by step Solutions of Exercise / lesson-4 Cubes and Cube-Roots ICSE Class-8th Concise Selina Mathematics. Our Solutions contain all type Questions with Exe-4A , Exe-4 B , to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-8.
Cubes and Cube-Roots ICSE Class-8th Concise Mathematics Selina Solutions Chapter-4
–: Select Topics :–
Exercise- 4 A Cubes and Cube-Roots ICSE Class-8th Concise
Question 1 :-
Find the cube of :
(i) 7
(ii) 11
(iii) 16
(iv) 23
(v) 31
(vi) 42
(vii) 54
Answer :-

Question 2 :-
Find which of the following are perfect cubes :
(i) 243
(ii) 588
(iii) 1331
(iv) 24000
(v) 1728
(vi) 1938
Answer :-
(i) 243
| 3 | 243 |
| 3 | 81 |
| 3 | 27 |
| 3 | 9 |
| 3 | 3 |
| 1 |
∵ 243 = 3 x 3 x 3 x 3 x 3
= (3 x 3 x 3) x 3 x 3
= 33 x 3 x 3
∴ 279 is not a perfect cube.
(ii) 588
| 2 | 588 |
| 2 | 294 |
| 7 | 147 |
| 7 | 21 |
| 3 | 3 |
| 1 |
588 = 2 x 2 x 7 x 7 x 3
∴ 588 is not perfect cube.
(iii) 1331
| 11 | 1331 |
| 11 | 121 |
| 11 | 11 |
| 1 |
∴ 1331 = 11 x 11 x 11 = (11)3
∴ 1331 is a perfect cube.
(iv) 24000
∵ 24000 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 5 x 5 x 5
= (2)2 x (2)3 x (5)3 x 3
∴ 24000 is not a perfect cube.
(v) 1728
| 2 | 1728 |
| 2 | 864 |
| 2 | 432 |
| 2 | 216 |
| 2 | 108 |
| 2 | 54 |
| 3 | 27 |
| 3 | 9 |
| 3 | 3 |
| 1 |
∵ 1728 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3
= (2)3 x (2)3 x (3)3
∵ 1728 is a perfect cube.
(vi) 1938
| 2 | 1938 |
| 3 | 936 |
| 17 | 323 |
| 19 | 19 |
| 1 |
1938 = 2 x 3 x 17 x 19
1938 is not a perfect cube.
Question 3 :-
Find the cubes of :
(i) 2.1
(ii) 0.4
(iii) 1.6
(iv) 2.5
(v) 0.12
(vi) 0.02
(vii) 0.8
Answer :-
(i) 2.1
= (2.1)3
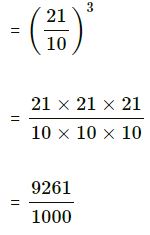
= 9.261
(ii) 0.4
= (0.4)3
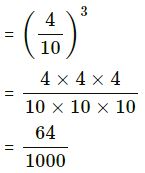
= 0.064
(iii) 1.6
= (1.6)3
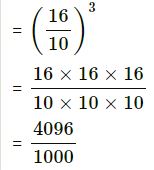
= 4.906
(iv) 2.5
= (2.5)3
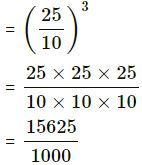
= 15.625
(v) 0.12
= (0.12)3
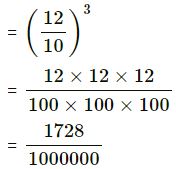
= 0.001728
(vi) 0.02
= (0.02)3
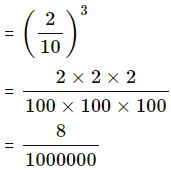
= 0.00000
(vii) 0.8
= (0.8)3
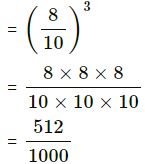
= 0.512
Question 4 :-
Find the cubes of :
(i) 3/7
(ii) 8/9
(iii) 10/13
(iv) 1 2/7
(v) 2 1/2
Answer :-
(i)
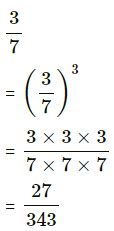
(ii)
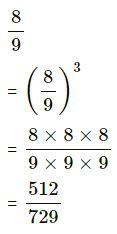
(iii)
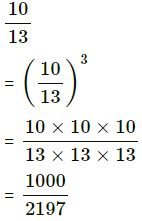
(iv)
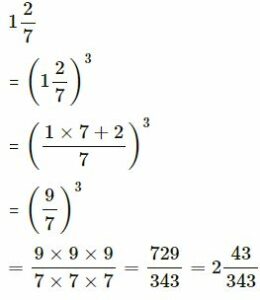
(v)
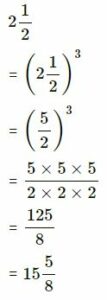
Question 5 :-
Find the cubes of :
(i) -3
(ii) -7
(iii) -12
(iv) -18
(v) -25
(vi) -30
(vii) -50
Answer :-
(i) -3
= (-3)3
= -3 x -3 x -3
= -(3 x 3 x 3)
= -27
(ii) -7
= (-7)3
= -7 x -7 x -7
= -(7 x 7 x 7)
=-343
(iii) -12
= (-12)3
= -12 x -12 x -12
= -(12 x 12 x 12)
= -1728
(iv) -18
= (-18)3
= -18 x -18 x -18
= -(18 x 18 x 18)
= -5832
(v) -25
= (-25)3
= -25 x -25 x -25
= -(25 x 25 x 25)
= -15625
(vi) -30
= (-30)3
= -30 x -30 x -30
= -(30 x 30 x 30)
= -27000
(vii) -50
= (-50)3
= -50 x -50 x -50
= -(50 x 50 x 50)
= -125000
Question 6 :-
Which of the following are cubes of:
(i) an even number
(ii) an odd number
216, 729, 3375, 8000, 125, 343, 4096 and 9261.
Answer :-
(i) an even number :
∵ 216 = 2 x 2 x 2 x 3 x 3 x 3
| 2 | 216 |
| 2 | 108 |
| 2 | 54 |
| 3 | 27 |
| 3 | 9 |
| 3 | 3 |
| 1 |
= (2)3 x (3)3
= (6)3
∵ 729 = 3 x 3 x 3 x 3 x 3 x 3
| 3 | 729 |
| 3 | 243 |
| 3 | 81 |
| 3 | 27 |
| 3 | 9 |
| 3 | 3 |
| 1 |
= (3)3 x (3)3
= (9)3
∵ 3375 = 5 x 5 x 5 x 3 x 3 x 3
| 5 | 3375 |
| 5 | 675 |
| 5 | 135 |
| 3 | 27 |
| 3 | 9 |
| 3 | 3 |
| 1 |
= (5)3 x (3)3
= (15)3
∵ 8000 = 20 x 20 x 20
= (20)3
| 5 | 125 |
| 5 | 25 |
| 5 | 5 |
| 1 |
125 = 5 x 5 x 5
= (5)3
∵ 343 = 7 x 7 x 7
= (7)3
| 7 | 343 |
| 7 | 49 |
| 7 | 7 |
| 1 |
∵ 4096 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
| 2 | 4096 |
| 2 | 2048 |
| 2 | 1024 |
| 2 | 512 |
| 2 | 256 |
| 2 | 128 |
| 2 | 64 |
| 2 | 32 |
| 2 | 16 |
| 2 | 8 |
| 2 | 4 |
| 2 | 2 |
| 1 |
= (2)3 x (2)3 x (2)3 x (2)3
=(16)3
Cubes of an even number are 216, 8000, 4096.
(ii) an odd number :
∵ 216 = 2 x 2 x 2 x 3 x 3 x 3
| 2 | 216 |
| 2 | 108 |
| 2 | 54 |
| 3 | 27 |
| 3 | 9 |
| 3 | 3 |
| 1 |
= (2)3 x (3)3
= (6)3
∵ 729 = 3 x 3 x 3 x 3 x 3 x 3
| 3 | 729 |
| 3 | 243 |
| 3 | 81 |
| 3 | 27 |
| 3 | 9 |
| 3 | 3 |
| 1 |
= (3)3 x (3)3
= (9)3
∵ 3375 = 5 x 5 x 5 x 3 x 3 x 3
| 5 | 3375 |
| 5 | 675 |
| 5 | 135 |
| 3 | 27 |
| 3 | 9 |
| 3 | 3 |
| 1 |
= (5)3 x (3)3
= (15)3
∵ 8000 = 20 x 20 x 20
= (20)3
| 5 | 125 |
| 5 | 25 |
| 5 | 5 |
| 1 |
125 = 5 x 5 x 5
= (5)3
∵ 343 = 7 x 7 x 7
= (7)3
| 7 | 343 |
| 7 | 49 |
| 7 | 7 |
| 1 |
∵ 4096 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
| 2 | 4096 |
| 2 | 2048 |
| 2 | 1024 |
| 2 | 512 |
| 2 | 256 |
| 2 | 128 |
| 2 | 64 |
| 2 | 32 |
| 2 | 16 |
| 2 | 8 |
| 2 | 4 |
| 2 | 2 |
| 1 |
(2)3 x (2)3 x (2)3 x (2)3
=(16)3
Cubes of an odd number are 729, 3375, 125, 343, 9261.
Question 7 :-
Find the least number by which 1323 must be multiplied so that the product is a perfect cube.
Answer :-
The prime factor of 1323 are =3 x 3 x 3 x 7 x 7
= (3 x 3 x 3) x 7 x 7
Clearly, 1323 must be multiplied by 7.
Question 8 :-
Find the smallest number by which 8768 must be divided so that the quotient is a perfect cube.
Answer :-
The prime factor of 8768 are
| 2 | 8768 |
| 2 | 4384 |
| 2 | 2192 |
| 2 | 1096 |
| 2 | 548 |
| 2 | 274 |
| 137 | 137 |
| 1 |
= 2 x 2 x 2 x 2 x 2 x 2 x 137
= (2 x 2 x 2) x (2 x 2 x 2) x 137
Clearly, 8768 must be divided by 137.
Question 9 :-
Find the smallest number by which 27783 be multiplied to get a perfect square number.
Answer :-
| 3 | 27783 |
| 3 | 9261 |
| 3 | 3087 |
| 3 | 1029 |
| 7 | 343 |
| 7 | 49 |
| 7 | 7 |
| 1 |
= 3 x 3 x 3 x 3 x 7 x 7 x 7
= (3 x 3 x 3) x (7 x 7 x 7) x 3
Clearly, 27783 must be multiplied by 3 x 3
= 9
Question 10 :-
With what least number must 8640 be divided so that the quotient is a perfect cube?
Answer :-
The prime factors of 8640 are
| 2 | 8640 |
| 2 | 4320 |
| 2 | 2160 |
| 2 | 540 |
| 2 | 270 |
| 3 | 135 |
| 3 | 45 |
| 3 | 15 |
| 5 | 5 |
| 1 |
= 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3 x 5
= (2 x 2 x 2) x (2 x 2 x 2) x (3 x 3 x 3) x 5
Clearly, 8640 must be divided by 5.
Question 11 :-
Which is the smallest number that must be multiplied to 77175 to make it a perfect cube?
Answer :-
The prime factor of 77175 are
| 3 | 77175 |
| 3 | 25725 |
| 5 | 8575 |
| 5 | 1715 |
| 7 | 343 |
| 7 | 49 |
| 7 | 7 |
| 1 |
= 3 x 3 x 5 x 5 x 7 x 7 x 7
= (7 x 7 x 7) x 3 x 3 x 5 x 5
Clearly, 77175 must be multiplied by 3 x 5
= 15
Exercise – 4 B Selina Solutions Cubes and Cube-Roots for ICSE Class-8th
Question 1 :-
Find the cube-roots of :
(i) 64
(ii) 343
(iii) 729
(iv) 1728
(v) 9261
(vi) 4096
(vii) 8000
(viii) 3375
Answer :-
(i) 64
= ³√643
= (2 x 2 x 2) x (2 x 2 x 2)
= 2 x 2
= 4
| 2 | 64 |
| 2 | 32 |
| 2 | 16 |
| 2 | 8 |
| 2 | 4 |
| 2 | 2 |
| 1 |
(ii) 343
= ³√343
= 7 x 7 x 7 = 7
| 7 | 343 |
| 7 | 49 |
| 7 | 7 |
| 1 |
(iii) 729
= ³√729
= (3 x 3 x 3) x (3 x 3 x 3)
= 3 x 3
=9
| 3 | 729 |
| 3 | 243 |
| 3 | 81 |
| 3 | 27 |
| 3 | 9 |
| 3 | 3 |
| 1 |
(iv) 1728
= ³√1728
= (2 x 2 x 2) x (2 x 2 x 2) x (3 x 3 x 3)
= 2 x 2 x 3
=12
| 2 | 1728 |
| 2 | 864 |
| 2 | 432 |
| 2 | 216 |
| 2 | 108 |
| 2 | 54 |
| 3 | 27 |
| 3 | 9 |
| 3 | 3 |
| 1 |
(v) 9261
= ³√9261
= (3 x 3 x 3) x (7 x 7 x 7)
= 3 x 7
= 21
| 3 | 9261 |
| 3 | 3087 |
| 3 | 1029 |
| 7 | 343 |
| 7 | 49 |
| 7 | 7 |
| 1 |
(vi) 4096
= ³√4096
= (2 x 2 x 2) x (2 x 2 x 2) x (2 x 2 x 2) x (2 x 2 x 2)
= 2 x 2 x 2 x 2
= 16
| 2 | 4096 |
| 2 | 2048 |
| 2 | 1024 |
| 2 | 512 |
| 2 | 256 |
| 2 | 128 |
| 2 | 64 |
| 2 | 32 |
| 2 | 16 |
| 2 | 8 |
| 2 | 4 |
| 2 | 2 |
| 1 |
(vii) 8000
= ³√8000
= (4 x 4 x 4) x (5 x 5 x 5)
= 4 x 5
=20
| 4 | 8000 |
| 4 | 2000 |
| 4 | 500 |
| 5 | 125 |
| 5 | 25 |
| 5 | 5 |
| 1 |
(viii) 3375
= ³√3375
= (5 x 5 x 5) x (3 x 3 x 3)
= 5 x 3
= 15
| 5 | 3375 |
| 5 | 675 |
| 5 | 135 |
| 5 | 27 |
| 3 | 9 |
| 3 | 3 |
| 1 |
Question 2 :-
Find the cube-roots of :
(i) 27/ 64
(ii) 125/216
(iii) 343/512
(iv) 64 x 729
(v) 64 x 27
(vi) 729 x 8000
(vii) 3375 x 512
Answer :-
(i)
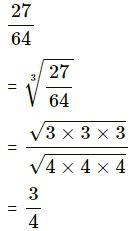
(ii)
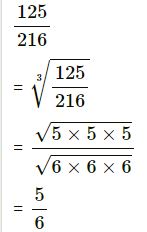
(iii)
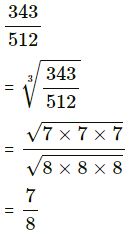
(iv) 64 x 729
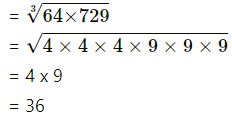
(v) 64 x 27
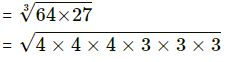
= 4 x 3
= 12
(vi) 729 x 8000
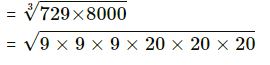
= 9 x 20
= 180
(vii) 3375 x 512
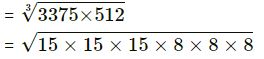
= 15 x 8
= 120
Question 3 :-
Find the cube-roots of :
(i) -216
(ii) -512
(iii) -1331
(iv) -27/125
(v) -64/343
(vi) -5`12/343
(vii) -2197
(viii) -5832
(ix) -2744000
Answer :-
(i) -216
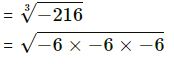
= -6
(ii) -512
= ³√-512
= √-8×-8×-8
= -8
(iii) -1331
= ³√-1331
= √-11×-11×-11
= -11
(iv)
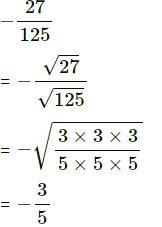
(v)
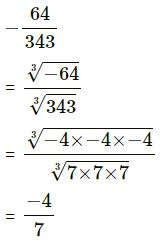
(vi)
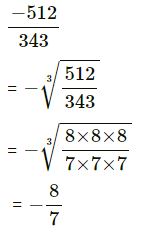
(vii) -2197
= ³√-2197
| 13 | 2197 |
| 13 | 169 |
| 13 | 13 |
| 1 |
= ³√-13×-13×-133
= -13
(viii) -5832
= ³√-5832
| 2 | 5832 |
| 2 | 2916 |
| 2 | 1458 |
| 3 | 729 |
| 3 | 243 |
| 3 | 81 |
| 3 | 27 |
| 3 | 9 |
| 3 | 3 |
| 1 |
= √-2×-2×-2×-3×-3×-3×-3×-3×-3
= – 2 x -3 x -3
= -18
(ix) -2744000
= ³√-2744000
| 2 | 2744000 |
| 2 | 1372000 |
| 2 | 686000 |
| 7 | 343000 |
| 7 | 49000 |
| 7 | 7000 |
| 10 | 1000 |
| 10 | 100 |
| 10 | 10 |
| 1 |
= √-2×-2×-2×-7×-7×-7×-10×-10×-10
= -2 x -7 x -10
= -140
Question 4:-
Find the cube-roots of :
(i) 2.744
(ii) 9.261
(iii) 0.000027
(iv) -0.512
(v) -15.625
(vi) -125 x 1000
Answer :-
(i) 2.744
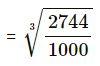
| 2 | 2744 |
| 2 | 1372 |
| 2 | 686 |
| 7 | 343 |
| 7 | 49 |
| 7 | 7 |
| 1 |
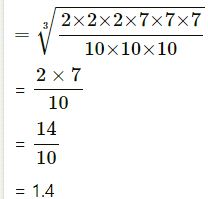
(ii) 9.261
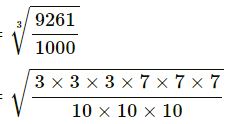
| 3 | 9261 |
| 3 | 3087 |
| 3 | 1029 |
| 7 | 343 |
| 7 | 49 |
| 7 | 7 |
| 1 |
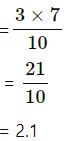
(iii) 0.000027
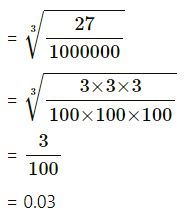
(iv) -0.512
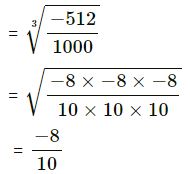
= -0.8
(v) -15.625
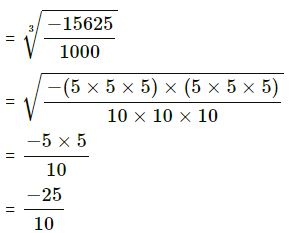
= – 2.5
| 5 | 15625 |
| 5 | 3125 |
| 5 | 625 |
| 5 | 125 |
| 5 | 25 |
| 5 | 5 |
| 1 |
(vi) -125 x 1000
= √-125×100
= √-(5×5×5)×(10×10×10)
= -5 x 10
= -50
Question 5 :-
Find the smallest number by which 26244 may be divided so that the quotient is a perfect cube.
Answer :-
The prime factors of 26244 are
| 2 | 26244 |
| 2 | 13122 |
| 3 | 6561 |
| 3 | 2187 |
| 3 | 729 |
| 3 | 243 |
| 3 | 81 |
| 3 | 27 |
| 3 | 9 |
| 3 | 3 |
| 1 |
= 2 x 2 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3
= (3 x 3 x 3) x (3 x 3 x 3) x 3 x 3 x 2 x 2
Clearly, 26244 must be divided by
3 x 3 x 2 x 2 = 36
Question 6 :-
What is the least number by which 30375 should be multiplied to get a perfect cube?
Answer :-
The prime factors of 30375 are
| 3 | 30375 |
| 3 | 10125 |
| 3 | 3375 |
| 3 | 1125 |
| 3 | 375 |
| 5 | 125 |
| 5 | 25 |
| 5 | 5 |
| 1 |
= 3 x 3 x 3 x 3 x 3 x 5 x 5 x 5
= (3 x 3 x 3) x (5 x 5 x 5) x 3 x 3
Clearly, 30375 must be multiplied with 3
Question 7 :-
Find the cube-roots of :
(i) 700 x 2 x 49 x 5
(ii) -216 x 1728
(iii) -64 x -125
(iv) -27/343
(v) 729/1331
(vi) 250.047
(vii) -175616
Answer :-
(i) 700 x 2 x 49 x 5
| 2 | 700 |
| 2 | 350 |
| 5 | 175 |
| 5 | 35 |
| 7 | 7 |
| 1 |
= 2 x 2 x 5 x 5 x 7 x 2 x 7 x 7 x 5
= (2 x 2 x 2) x (5 x 5 x 5) x (7 x 7 x 7)
= 2 x 5 x 10
=70
(ii) -216 x 1728
| 2 | 216 |
| 2 | 108 |
| 2 | 54 |
| 3 | 27 |
| 3 | 9 |
| 3 | 3 |
| 1 |
| 2 | 1728 |
| 2 | 864 |
| 2 | 432 |
| 216 |
= -(2 x 2 x 2 x 3 x 3 x 3) x (2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3)
= -2 x 3 x 2 x 2 x 3
= -72
(iii) -64 x -125
-64 x -125
= -(4 x 4 x 4) x -(5 x 5 x5)
= -4 x -5
= 20
(iv)
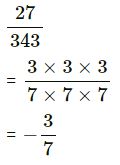
(v)
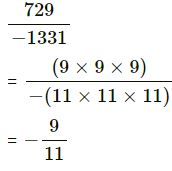
(vi) 250.047
= 250047/1000
| 3 | 250047 |
| 3 | 83349 |
| 3 | 27783 |
| 3 | 9261 |
| 3 | 3087 |
| 3 | 1029 |
| 7 | 343 |
| 7 | 49 |
| 7 | 7 |
| 1 |
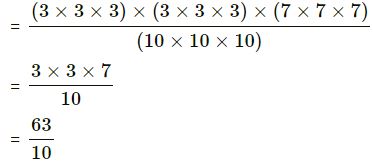
(vii) -175616
| 2 | 175616 |
| 2 | 27808 |
| 2 | 43904 |
| 2 | 21952 |
| 2 | 10976 |
| 2 | 5488 |
| 2 | 2744 |
| 2 | 1372 |
| 2 | 686 |
| 7 | 343 |
| 7 | 49 |
| 7 | 7 |
| 1 |
= -[(2 x 2 x 2) x (2 x 2 x 2) x (2 x 2 x 2) x (7 x 7 x 7)]
=-[2 x 2 x 2 x 7]
= -56
— End of Cubes and Cube-Roots Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -8
Thanks