Data Handling ICSE Class-7th Concise Selina Mathematics Solutions Chapter-21. We provide step by step Solutions of Exercise / lesson-21 Data Handling for ICSE Class-7 Concise Selina Mathematics. Our Solutions contain all type Questions with Exe-21 A and Exe-21 B to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-7 Mathematics .
Data Handling ICSE Class-7th Concise Selina Mathematics Solutions Chapter-21
–: Select Topics :–
Selina Solutions Exercise – 21 A Data Handling ICSE Class-7th Concise Mathematics
Question 1.
Consider the following numbers :
68, 76, 63, 75, 93, 83, 70, 115, 82, 105, 90, 103, 92, 52, 99, 73, 75, 63, 77 and 71.
(i) Arrange these numbers in ascending order.
(ii) What the range of these numbers?
Answer
(i) In ascending order. We get,
52, 63, 63, 68, 70, 71, 73, 75, 75, 76, 77, 82, 83, 90, 92, 93, 99, 103, 105, 115
(ii) Range of given numbers = Largest number – Smallest number
= 115 – 52 = 48
Question 2.
Represent the following data in the form of a frequency distribution table :
16, 17, 21, 20, 16, 20, 16, 18, 17, 21, 17, 18, 19, 17, 15, 15, 19, 19, 18, 17, 17, 15, 15, 16, 17, 17, 19, 18, 17, 16, 15, 20, 16, 17, 19, 18, 19, 16, 21 and 17.
Answer
The frequency distribution for these data :
| Numbers | Tally marks | Frequency |
| 15 | |||| | 5 |
| 16 | |||| || | 7 |
| 17 | |||| |||| | | 11 |
| 18 | |||| | 5 |
| 19 | |||| | | 6 |
| 20 | ||| | 3 |
| 21 | ||| | 3 |
| Total | 40 |
Question 3.
A die was thrown 20 times and following scores were recorded.
2, 1, 5, 2, 4, 3, 6, 1, 4, 2, 5, 1, 6, 2, 6, 3, 5, 4, 1 and 3.
Prepare a frequency table for the scores.
Answer
The frequency table for the scores :
| No. of thrown dies | Tally marks | Frequency |
| 1 | |||| | 4 |
| 2 | |||| | 4 |
| 3 | ||| | 3 |
| 4 | ||| | 3 |
| 5 | ||| | 3 |
| 6 | ||| | 3 |
| Total | 20 |
Question 4.
Following data shows the weekly wages (in ₹) of 10 workers in a factory.
3500, 4250, 4000, 4250, 4000, 3750, 4750, 4000, 4250 and 4000
(i) Prepare a frequency distribution table.
(ii) What is the range of wages (in ₹)?
(iii) How many workers are getting the maximum wages?
Answer
(i) The frequency table for the wages of 10 workers:
| Weekly wages in (₹) | Tally marks | Frequency |
| 3500 | | | 1 |
| 3750 | | | 1 |
| 4000 | |||| | 4 |
| 4250 | ||| | 3 |
| 4750 | | | 1 |
| Total | 10 |
(ii) Range of wages (₹) = ₹4750 – ₹3500
= ₹1250
(iii) One
Question 5.
The marks obtained by 40 students of a class are given below :
80, 10, 30, 70, 60, 50, 50, 40, 40, 20, 40, 90, 50, 30, 70, 10, 60, 50, 20, 70, 70, 30, 80, 40,20, 80, 90, 50, 80, 60, 70, 40, 50, 60, 90, 60, 40, 40, 60 and 60
(i) Construct a frequency distribution table.
(ii) Find how many students have marks equal to or more than 70?
(iii) How many students obtained marks below 40?
Answer
(i) The frequency distribution table:
| Numbers | Tally marks | Frequency |
| 10 | || | 2 |
| 20 | ||| | 3 |
| 30 | ||| | 3 |
| 40 | |||| || | 7 |
| 50 | |||| | | 6 |
| 60 | |||| || | 7 |
| 70 | |||| | 5 |
| 80 | |||| | 4 |
| 90 | ||| | 3 |
| Total | 40 |
(ii) Students have marks equal to or more than 70 = 5 + 4 + 3
= 12
(iii) Students obtained marks below 40 = 2 + 3 + 3
= 8 students
Question 6.
Arrange the following data in descending order:
3.3, 3.2, 3.1, 3.7, 3.6, 4.0, 3.5, 3.9, 3.8, 4.1, 3.5, 3.8, 3.7, 3.9 and 3.4.
(i) Determine the range.
(ii) How many numbers are less than 3.5?
(iii) How many numbers are 3.8 or above?
Answer
(i)
In descending order:
4.1, 4.0, 3.9, 3.9, 3.8, 3.8, 3.7, 3.7, 3.6, 3.5, 3.5, 3.4, 3.3, 3.2, 3.1
Range = 4.1 – 3.1 = 1
(ii)
In descending order:
4.1, 4.0, 3.9, 3.9, 3.8, 3.8, 3.7, 3.7, 3.6, 3.5, 3.5, 3.4, 3.3, 3.2, 3.1
Number less than 3.5 = 4
ex. 3.4, 3.3, 3.2, 3.1
(iii)
In descending order:
4.1, 4.0, 3.9, 3.9, 3.8, 3.8, 3.7, 3.7, 3.6, 3.5, 3.5, 3.4, 3.3, 3.2, 3.1
Number are 3.8 or above = 6
ex. 3.8, 3.8, 3.9, 3.9, 4.0, 4.1
Concise Maths Data Handling Exe-21 B for ICSE Class-7th Selina Solutions
Question 1.
Find the mean of 53, 61, 60, 67 and 64.
Answer
Mean of 53, 61, 60, 67 and 64
∴ Mean =(53+61+60+67+64)/5 …..(Here n = 5)
= 305/5
= 61
Question 2.
Find the mean of first six natural numbers.
Answer
First six natural numbers are:
1, 2, 3, 4, 5, 6
∴ Mean =(1+2+3+4+5+6)/6 …..(Here n = 6)
= 21/6
= 3.5
Question 3.
Find the mean of first ten odd natural numbers.
Answer
First ten odd natural numbers are :
1, 3, 5, 7, 9, 11, 13, 15, 17, 19
∴ Mean =(1+3+5+7+9+11+13+15+17+19)/10 …..(Here n = 10)
= 100/10
= 10
Question 4.
Find the mean of all factors of 10.
Answer
The factor of 10 are 2 and 5
∴ Mean =(2+5)/2 …………(Here n = 2)
= 7/2
= 3.5
Question 5.
Find the mean of x + 3, x + 5, x + 7, x + 9 and x + 11.
Answer
Mean of x + 3, x + 5, x + 7, x + 9 and x + 11
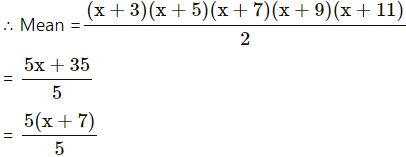
= x + 7
Question 6.
If different values of variable x are 19.8,15.4,13.7,11.71,11.8, 12.6,12.8,18.6,20.5 and 2.1, find the mean.
Answer
19.8 +15.4 +13.7 +11.71 +11.8 +12.6 + 12.8 +18.6 + 20.5 +21.1
so Mean =(19.8+15.4+13.7+11.71+11.8+12.6+12.8+18.6+20.5+21.1)/10
= 158.01/10
= 15.801
Question 7.
The mean of a certain number of observations is 32. Find the resulting mean, if each observation is,
(i) increased by 3
(ii) decreased by 7
(iii) multiplied by 2
(iv) divided by 0.5
(v) increased by 60%
(vi) decreased by 20%
Answer
(i)
Increased by = 3
Observed mean = 32
If increased by 3
so Resulting mean
= 32 + 3
= 35
(ii)
Observed mean = 32
Decreased by = 7
∴ Resulting mean
= 32 − 7
= 25
(iii)
Observed mean = 32
Multiplied by = 2
so Resulting mean
= 32 × 2
= 64
(iv)
Observed mean = 32
Divided by = 0.5
so Resulting mean
= 32/0.5
=64
(v)
Observed mean = 32
Increased by = 60%
∴ Resulting mean = 32+(60/100)
= (3200+60)/100
=3260/100
=32.6
(vi)
Observed mean = 32
Decreased by = 20%
∴ Resulting mean = 32-(20/100)
= (3200-20)/100
=3180/100
=31.8
Question 8.
The pocket expenses (per day) of Anuj, during a certain week, from monday to Saturday were ₹85.40, ₹88.00, ₹86.50, ₹84.75, ₹82.60 and ₹87.25. Find the mean pocket expenses per day.
Answer
The pocket expenses (per day) during a certain week are: ₹85.40, ₹88.00, ₹86.50, ₹84.75, ₹82.60 and ₹87.25
∴ Mean of pocket expenses per day
=(85.40+88.00+86.50+84.75+82.60+87.25)/6 ……(Here n = 6)
= 514.5/6
= ₹85.75
so Anuj expenses per day
= ₹85.75
Question 9.
If the mean of 8, 10, 7, x + 2 and 6 is 9, find the value of x.
Answer
The mean 8, 10, 7, x + 2 and 6 is 9
so (8+10+7+x+2+6)/6=9
⇒ (x+33)/6=9
⇒ x + 33 = 9 × 6
⇒ x = 54 − 33
⇒ x = 21
Question 10.
Find the mean of first six multiples of 3.
Answer
The six multiples of 3 are 3, 6, 9, 12, 15, 18
∴ Mean = (3+6+9+12+15+18)/6 ……….(Here n = 6)
= 63/3
= 10.5
Question 11.
Find the mean of first five prime numbers.
Answer
The first five prime numbers are 2, 3, 5, 7, 11
∴ Mean = (2+3+5+7+11)/5 (Here n = 5)
= 28/5
=5 (3/5)
=5.6
Question 12.
The mean of six numbers :x-5,x- 1, x, x + 2, x + 4 and x + 12 is 15. Find the mean of first four numbers.
Answer
The mean of six numbers are x – 5, x – 1, x, x + 2, x + 4 and x + 12 is 15
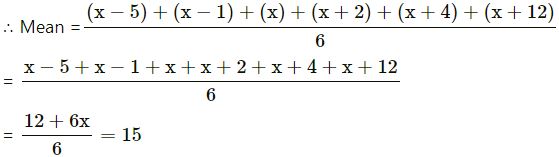
⇒ 12 + 6x = 90
⇒ 6x = 90 − 12
⇒ 6x = 78
⇒ x = 786
=13
x = 13
∴ The six numbers are (13 − 5), (13 − 1), 13, (13 + 2), (13 + 4), (13 + 12)
ex. 8, 12, 13, 15, 17, 25
Now, mean of first four numbers
= 
Question 13.
Find the mean of squares of first five whole numbers.
Answer
First five whole numbers are 0, 1, 2, 3, 4
Then square the whole prime numbers
= (0)2, (1)2, (2)2, (3)2, (4)2
= 0, 1, 4, 9, 16
so Mean = (0+1+4+9+16)/5 (Here n = 5)
= 30/5
= 6
Question 14.
If the mean of 6, 4, 7, p and 10 is 8, find the value of p.
Answer
The mean of 6, 4, 7, p and 10 is 8
∴ Mean = (6+4+7+p+10)/5=8
⇒ 27 + p = 40
⇒ p = 40 − 27
⇒ p = 13
Question 15.
Find the mean of first six multiples of 5.
Answer
Six multiples of 5 are 5, 10, 15, 20, 25 and 30
∴ Mean = (5+10+15+20+25+30)/6 (Here n = 6)
= 105/6
=17.5
Question 16.
The rainfall (in mm) in a city on 7 days of a certain week is recorded as follows

Find the total and average (mean) rainfall for the week.
Answer
The rainfall in a city on 7 days are 0.5, 2.7, 2.6, 0.5, 2, 5.8, 1.5
Average rainfall = (0.5+2.7+2.6+0.5+2+5.8+1.5)/7 (Number of days = 7)
= 15.6/7
= 2.2 mm
Question 17.
The mean of marks scored by 100 students was found to be 40, later on it was discovered that a score of 53 was misread as 83. Find the correct mean.
Answer
Mean of 40 observations = 100
Total sum of 40 observations = 100 × 40
= 4000
Incorrect total of 40 observation is = 4000
Correct total of 40 observations = 4000 – 83 + 53
= 3970
so Correct mean = 3970/100
= 39.70
Question 18.
The mean of five numbers is 27. If one number is excluded, the mean of remaining numbers is 25. Find the excluded number.
Answer
Mean of 5 observations = 27
Total sum of 5 observations = 27 × 5
= 135
On excluding an observation, the mean of remaining 6 observations = 25
⇒ Total of remaining 4 observations = 25 × 4
= 100
⇒ Included observation = Total mean of 5 observations – Total mean of 4 observations
= 135 − 100
= 35
Question 19.
The mean of 5 numbers is 27. If one new number is included, the new mean is 25. Find the included number.
Answer
Mean of 5 observations = 27
Total sum of 5 observations = 27 × 5
= 135
On including an observation the mean of 6 observation = 25 × 6
= 150
⇒ Included observations = Total Mean of 6 observations – Total mean of 5 observations
= 150 − 135
= 15
Question 20.
Mean of 5 numbers is 20 and mean of other 5 numbers is 30. Find the mean of all the 10 numbers taken together.
Answer
The mean of 5 number = 20
Then, mean of other 5 number = 30
∴ Mean =(20+30)/2
=50/2
=25
Question 21.
Find the median of:
(i) 5,7, 9, 11, 15, 17,2, 23 and 19
(ii) 9, 3, 20, 13, 0, 7 and 10
(iii) 18, 19, 20, 23, 22, 20, 17, 19, 25 and 21
(iv) 3.6, 9.4, 3.8, 5.6, 6.5, 8.9, 2.7, 10.8, 15.6, 1.9 and 7.6.
Answer
(i)
5, 7, 9, 11, 15, 17, 2, 23 and 19
In ascending order:
2, 5, 7, 9, 11, 15, 17, 19, 23
Here, number of terms = 9 which is odd
Median = (n+1)/2
=(9+1)/2th term
= 5th term = 11
Hence,
median = 11
(ii)
9, 3, 20, 13, 0, 7 and 10
In ascending order:
0, 3, 7, 9, 10, 13, 20
Here, number of terms = 7 which is odd
∴ Median = (n+1)/2
=(7+1)/2 th term = 4th term
= 9
Hence,
median = 9
(iii)
18, 19, 20, 23, 22, 20, 17, 19, 25 and 21
In ascending order:
17, 18, 19, 19, 20, 20, 21, 22, 23, 25
Here, numbers of terms = 10 which is even.
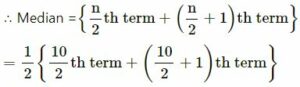
= (1/2) {5th term + 6th term}
= (1/2) {20 + 20}
= (1/2)×20 = 20
Hence,
median = 20
(iv)
3.6, 9.4, 3.8, 5.6, 6.5, 8.9, 2.7, 10.8, 15.6, 1.9 and 7.6.
In ascending order:
1.9, 2.7, 3.6, 3.8, 5.6, 6.5, 7.6, 8.9, 9.4, 10.8, 15.6
Here,
number of terms = 11 which is odd
so Median = (n+1)/2
=(11+1)/2 = 6th term
= 6yh term = 6.5
Hence,
median = 6.5
Question 22.
Find the mean and the mode for the following data :

Answer
We prepare the table given below:
| Term (xi) |
Frequency (fi) |
(fixi) |
| 18 | 3 | 54 |
| 22 | 5 | 110 |
| 26 | 10 | 260 |
| 30 | 2 | 60 |
| 34 | 8 | 276 |
| 38 | 2 | 76 |
| Total | 30 | 832 |
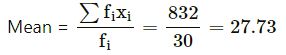
Since the frequency of Number 26 is maximum.
∴ Mode = 26
Question 23.
Find the mode of:
(i) 5, 6, 9, 13, 6, 5, 6, 7, 6, 6, 3
(ii) 7, 7, 8, 10, 10, 11, 10, 13, 14
Answer
(i)
In ascending order:
3, 5, 5, 6, 6, 6, 6, 6, 7, 9, 13
Mostly repeated term = 6
so Mode = 6
(ii)
In ascending order = 7, 7, 8, 10, 10, 10, 11, 13, 14
Mostly repeated term =10
so Mode = 10
Question 24.
Find the mode of :

Answer
(i) The frequency of number 18 is maximum
∴ Mode = 18
(ii) The frequency of number 41 is maximum
∴ Mode = 41
Question 25.
The heights (in cm) of 8 girls of a class are 140,142,135,133,137,150,148 and 138 respectively. Find the mean height of these girls and their median height.
Answer
In ascending order:
133, 135, 137, 138, 140, 142, 148, 150
Here, the number of girls = 8 which is even
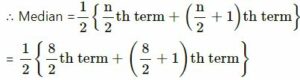
= 12 {4th term + 5th term}
= (1/2) {138 + 140} cm
= (1/2)×278
= 139 cm
∴ Mean = (133+135+137+138+140+142+148+150)/8
= 1123/8 cm
= 140.375 cm
Question 26.
Find the mean, the median and the mode of:
(i) 12, 24, 24, 12, 30 and 12
(ii) 21, 24, 21, 6, 15, 18, 21, 45, 9, 6, 27 and 15.
Answer
(i)
12, 24, 24, 12, 30 and 12
∴ Mean = (12+24+24+12+30+12)/6
= 114/6
=19
Numbers are 12, 24, 24, 12, 30 and 12
Mostly repeated term = 12
∴ Mode = 12
Now, In ascending order
= 12, 12, 12, 24, 24, 30
Here, number of terms 6 which is even

= 1/2 {12 + 24}
= (1/2)×36
= 18
∴ Median = 18
(ii)
21, 24, 21, 6, 15, 18, 21, 45, 9, 6, 27 and 15
∴ Mean
= (21+24+21+6+15+18+21+45+9+6+27+15)/12
= 22812=19
Numbers are 21, 24, 21, 6, 15, 18, 21, 45, 9, 6, 27 and 15
Mostly repeated term = 21
∴ Mode = 21
Now, In ascending order
= 6, 6, 9, 15, 15, 18, 21, 21, 21, 24, 27, 45
Here, number of terms = 12 which is even
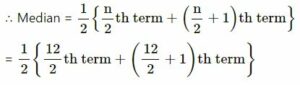
= 1/2 {6th term + 7th term}
= 1/2 {18 + 21}
= (1/2)×39
= 19.5
Question 27.
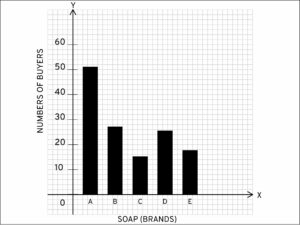
The following table shows the market positions of some brands of soap.
Draw a suitable bar graph :

Answer
Question 28.
The birth rate per thousand of different countries over a particular period of time is shown below.

Answer
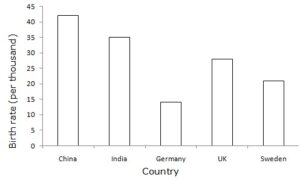
— End of Data Handling ICSE Class-7th Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -7
Thanks


