Electric Potential Numerical on Electrostatic Potential Energy Class-12 Nootan ISC Physics Solutions Ch-3. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-12 Physics.
Electric Potential Numerical on Electrostatic Potential Energy Class-12 Nootan ISC Physics Solutions Ch-3
| Board | ISC |
| Class | 12 |
| Subject | Physics |
| Book | Nootan |
| Chapter-3 | Electric Potential |
| Topics | Numerical on Electrostatic Potential Energy |
| Academic Session | 2025-2026 |
Numerical on Electrostatic Potential Energy
Electric Potential Numerical on Electrostatic Potential Energy Class-12 Nootan ISC Physics Solutions Ch-3
Que-22: The mutual electric potential energy between two protons in a uranium nucleus is 2.4 x 10^5 eV. Find the distance between the protons.
Ans: According to the formula of Potential Energy,
U = k q1q2/r {q1 = q2 = 1.6 x 10^-19 C}
=> r = k q^2/U
=> r = 1.6 x 10^-19 x 9 x 10^9 / 2.4 x 10^5 x 1.6 x 10^-19
{1 eV = 1.6 x 10^-19 C}
=> r = 6 × 10^-15 m
Hence, the distance between the protons is 6 × 10^-15 m
Que-23: An electron is circulating around the nucleus of a hydrogen atom in a circular orbit of radius 5.3 × 10^-11 m. Calculate the electric potential at this radius and electric potential energy of the atom in eV. What would be the electric potential due to a helium nucleus at the same radius?
Ans: (i) Charge on hydrogen nucleoles is 1.6 x 10^-19 C
∴ Electric potential at radius 5.3 x 10^-11 m
V = k q/r
= 9 x 10^9 x 1.6 x 10^-19 / 5.3 x 10^-11
= 27.2 V
(ii) Electric potential energy due to electron
U = k e.(-e)/r
= -9 x 10^9 x (1.6 x 10^-19)^2 / 5.3 x 10^-11
energy in electron volt (eV)
= -9 x 10^9 x 1.6 x 10^-19 / 5.3 x 10^-11 {1 eV = 1.6 x 10^-19 J}
= -27.2 eV
(iii) in case of helium atom charge on nucleolus = 3.2 x 10^-19 C
∴ Potential at its radius
V = k 3.2 x 10^-19 / 5.3 x 10^-11
V = 9 x 10^9 x 3.2 x 10^-19 / 5.3 x 10^-11 = 54.4 V
Que-24: Three point-charges q1 (= −1 μC), q2 (= +2 μC) and 43 (= -1 µC) are placed in air in a line. The distance between q1 and q2 is 1 m and that between q2 and q3 is also 1 m. Calculate the electrostatic energy of the system.
Ans: U = k ∑qiqj / rij
= 9 x 10^9 [(-1 x 2 x 10^-12 / 1) + (2 x -1 x 10^-12 / 1) + (-1 x -1 x 10^-12 / 1)]
= 9 x 10^-3 x -3.5
= -31.5 x 10^-3 J
= -31.5 mJ
Que-25: Three equal charges of 5.0 µC each are placed at the three vertices of an equilateral triangle of side 5.0 cm each. Calculate the electrostatic potential energy of the system of charges.
Ans: U = k ∑qiqj / rij
=> U = 9 x 10^9 [5 x 5 x 10^-12 / 5 x 10^-2] x 3
=> 135 x 10^-1 J
=> 13.5 J
Que-26: Two positive charges of 10 µC each are situated 10 cm apart from each other. What is the increase in the electrostatic potential energy of the system when the two charges are brought closer by 2 cm?
Ans: U1 = k 10 x 10 x 10^-12 / 10 x 10^-2
= 9 x 10^9 x 10 x 10^-10 = 9 J
U2 = 9 x 10^9 x 10 x 10 x 10^-12 / 8 x 10^-2
=> 900/8 x 10^-1
=> 11.25 J
increase in energy = U2-U1
=> 11.25 – 9
=> 2.25 J
Que-27: (i) Calculate the work required to assemble each of the systems of charges (which is same as the electrostatic potential energy of the system) shown in Fig. (a) and (b). (ii) A charge q0 is brought from infinity to the centre of the square, the four charges being held fixed at its corners. How much extra work is needed to do this?
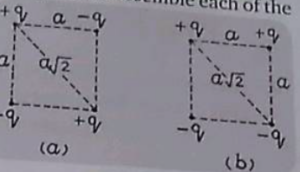
Ans: Work done = Potential Energy = k ∑qiqj / rij
(a) k [-q^2/a – q^2/a -q^2/a – q^2/a + q^2/a√2 + (-q)(-q)/a√2]
= k [-4q^2/a + 2q^2/a√2]
= -q^2/4πε0 (4 – √2)
(b) k [-q^2/a + q^2/a -q^2/a – q^2/a√2 – q^2/a√2 + (-q)(-q)/a]
= k [-2q^2/a√2]
= (-q^2/4πε0a) √2
Que-28: The distance between two protons is 1.0 × 10^-10 m. If they are made free, what will be the kinetic energy of each when they are away at a very large distance from each other? If one proton is kept fixed and only other is freed then what will be its kinetic energy?
Ans: (i) In case when both the protons are released total potential energy will be equally distributed in between two protons therefore energy of one proton will be
U/2 = 1/2 x k x e^2/r
= 1/2 x 9 x 10^9 x (1.6 x 10^-19)^2/ 1.0 x 10^-10
= 1.15 x 10^-18 J
(ii) and if only one proton is released then total energy will be acquired by only one proton
i.e. 2.30 x 10^-18 J
Que-29: Two electrons are released towards each other with equal velocities of 10^6 m/s. What will be the closest approach between them?
Ans: at closest approach all their kinetic energy will convert into potential energy
i.e. U = 2 x 1/2 mv^2
= k e^2/r = mv^2 = 9 x 10^-31 x (10^6)^2
=> r = (1.36 x 10^-19)^2 x 9 x 10^9 / 9 x 10^-31 x 10^12
= 2.56 x 10^-10 m
— : End Electric Potential Numerical on Electrostatic Potential Energy Class-12 Nootan ISC Physics. :–
Return to : – Nootan Solutions for ISC Class-12 Physics
Thanks
Please share with your friends


