ML Aggarwal Equation of Straight Line Exe-12.2 Class 10 ICSE Maths Solutions

ML Aggarwal Equation of Straight Line Exe-12.2 Class 10 ICSE Maths Solutions. We Provide Step by Step Answer of Exe-12.2 Questions for Equation of Straight Line as council prescribe guideline for upcoming board exam. Visit official Website CISCE  for detail information about ICSE Board Class-10.

ML Aggarwal Equation of Straight Line Exe-12.2 Class 10 ICSE Maths Solutions

Board	ICSE
Subject	Maths
Class	10th
Chapter-12	Equation of Straight Line
Writer / Book	Understanding
Topics	Solutions of Exe-12.2
Academic Session	2024-2025

Equation of Straight Line Exe-12.2

ML Aggarwal Class 10 ICSE Maths Solutions

Question- 1

State which one of the following is true : The straight lines y = 3x – 5 and 2y = 4x + 7 are
(i) parallel
(ii) perpendicular
(iii) neither parallel nor perpendicular.

Answer- 1

Slope of line y = 3x – 5 = 3
and slope of line 2y = 4x + 7
⇒ y = 2x + 7/2 = 2.
∴ Slope of both the lines are neither equal nor their product is – 1.
∴ These line are neither parallel nor perpendicular.

Question- 2 

If 6x + 5y – 7 = 0 and 2px + 5y + 1 = 0 are parallel lines, find the value of p.

Answer -2

In equation
6x + 5 y – 7 = 0
⇒ 5y = -6x + 7

y = (-6/5) x + 7/5

So, the slope of the line (m₁) = -6/5

Again, in equation 2px + 5y + 1 = 0

5y = -2px – 1

y = (-2p/5) x – 1/5

So, the slope of the line (m₂) = -2p/5

For these two lines to be parallel

m₁ = m₂

-6/5 = -2p/5

p = (-6/5) x (-5/2)

Thus, p = 3

Question -3

Lines 2x – by + 5 = 0 and ax + 3y = 2 are parallel. Find the relation connecting a and b. 

Answer- 3

In equation 2x – by + 5 = 0

and ax + 3y = 2

If two lines to be parallel then their slopes must be equal.

In equation 2x – by + 5 = 0,

by = 2x + 5

y = (2/b) x + 5/b

So, the slope of the line (m₁) = 2/b

And in equation ax + 3y = 2,

3y = -ax + 2

y = (-a/3) x + 2/3

So, the slope of the line (m₂) = (-a/3)

As the lines are parallel

m₁ = m₂

2/b = -a/3

6 = -ab

Hence, the relation connecting a and b is ab + 6 = 0

Question -4

If the straight lines 3x – 5y = 7 and 4x + ay + 9 = O are perpendicular to one another, find the value of a (2018)

Answer-4

Given lines are
3x – 5y = 1 ……….(i) and 4x + ay + 9 = 0  …………(ii)
Slope of line (i) (m₁) =  −(3/−5)=3/5
Slope of line (ii) (m₂) = −(4/𝑎)

Also, given that two lines are perpendicular to one and another
∴ (m₁) (m₂) = – 1

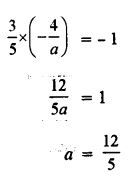
Hence, the value of a = 12/5 .

Question- 5  

If the lines 3x + by + 5 = 0 and ax – 5y + 7 = 0 are perpendicular to each other, find the relation connecting a and b.

Answer -5

Given
In the equation 3x + by + 5 = 0

and ax – 5y + 7 = 0 are perpendicular to each other

Then the product of their slopes must be -1.

Slope of line 3x + by + 5 = 0 is,

by = -3x – 5

y = (-3/b) – 5/b

So, slope (m₁) = -3/b

And,

The slope of line ax – 5y + 7 = 0 is

5y = ax + 7

y = (a/5) x + 7/5

So, slope (m₂) = a/5

As the lines are perpendicular, we have

m₁ x m₂ = -1

-3/b x a/5 = -1

-3a/5b = -1

-3a = – 5b

3a = 5b

Hence, the relation connecting a and b is 3a = 5b.

Question-6

Is the line through ( – 2, 3) and (4, 1) perpendicular to the line 3x = y + 1 ?
Does the line 3x = y + 1 bisect the join of ( – 2, 3) and (4, 1). 

Answer -6

Slope of the line passing through the points
(-2, 3) and (4, 1)

m₁ = y₂ – y₁/ x₂ – x₁

= (1 – 3)/ (4 + 2)

= -2/6

= -1/3

And, the slope of the line: 3x = y + 1

y = 3x -1

Slope (m₂) = 3

Now,

m₁ x m₂ = -1/3 x 3 = -1

Thus, the lines are perpendicular to each other as the product of their slopes is -1.

Now,

Co-ordinates of the mid-point of the line joining the points (-2, 3) and (4, 1) is

([-2 + 4]/2, [3 + 1]/2) = (1, 2)

Now, if the line 3x = y + 1 passes through the mid-point then it will satisfy the equation

3(1) = (2) + 1

3 = 3

Hence, the line 3x = y + 1 bisects the line joining the points (– 2, 3) and (4, 1).

Question -7

The line through A ( – 2, 3) and B (4, b) is perpendicular to the line 2x – 4y = 5. Find the value of b. (2012)

Answer -7

Gradient (m₁) of the line passing through the
points A (-2, 3) and B (4, b)

m₁ = (b – 3)/ (4 + 2) = (b – 3)/ 6

Now, the gradient of the given line 2x – 4y = 5 is

4y = 2x + 5

y = (2/4) x + 5/4

y = ½ x + 5/4

So, m₂ = ½

As the line are perpendicular to each other, we have

m₁ x m₂ = -1

(b – 3)/ 6 × ½ = -1

(b – 3)/ 12 = -1

b – 3 = -12

b = -12 + 3 = -9

Hence,

the value of b is -9.

Question-8  

If the lines 3x + y = 4, x – ay + 7 = 0 and bx + 2y + 5 = 0 form three consecutive sides of a rectangle, find the value of a and b.

Answer -8

Given lines are:

3x + y = 4 … (i)

x – ay + 7 = 0 … (ii)

bx + 2y + 5 = 0 … (iii)

It’s said that these lines form three consecutive sides of a rectangle.

So,

Lines (i) and (ii) must be perpendicular

Also, lines (ii) and (iii) must be perpendicular

We know that, for two perpendicular lines the product of their slopes will be -1.

Now,

Slope of line (i) is

3x + y = 4 ⇒ y = -3x = 4

Hence, slope (m₁) = -3

And, slope of line (ii) is

x – ay + 7 = 0 ⇒ ay = x + 7

y = (1/a) x + 7/a

Hence, slope (m₂) = 1/a

Finally, the slope of line (iii) is

bx + 2y + 5 = 0 ⇒ 2y = -bx – 5

y = (-b/2) x – 5/2

Hence, slope (m₃) = -b/2

As lines (i), (ii) and (iii) are consecutive sides of rectangle, we have

m₁ x m₂ = -1 and m₂ x m₃ = -1

(-3) x (1/a) = -1 and (1/a) x (-b/2) = -1

-3 = -a and -b/2a = -1

a = 3 and b = 2a ⇒ b = 2(3) = 6

Thus, the value of a is 3 and the value of b is 6.

Question -9

Find the equation of a line, which has the y-intercept 4, and is parallel to the line 2x – 3y – 7 = 0. Find the coordinates of the point where it cuts the x-axis. 

Answer -9

In the given line 2x – 3y – 7 = 0
⇒ 3y = 2x – 7
⇒ y = (2/3) x – 7/3

⇒ m = 2/3

So, the equation of the line parallel to the given line will be 2/3

Also given, the y-intercept is 4 = c

Hence, the equation of the line is given by

y = mx + c

y = (2/3) x + 4

3y = 2x + 12

2x – 3y + 12 = 0

Now, when this line intersects the x-axis the y co-ordinate becomes zero.

So, putting y = 0 in the line equation, we get

2x – 3(0) + 12 = 0

2x + 12 = 0

x = -12/2 = 6

Hence,

the co-ordinates of the point where it cuts the x-axis is (-6, 0).

Question -10

Find the equation of a straight line perpendicular to the line 2x + 5y + 7 = 0 and with y-intercept – 3 

Answer -10

In the line 2x + 5y + 7 = 0
⇒ 5y = – 2x – 7
⇒ y = (-2/5) – 7/5

⇒ m = -2/5

Now, let the slope of the line perpendicular to this line be m’

Then,

m x m’ = -1

(-2/5) x m’ = -1

⇒ m’ = 5/2

Also given, the y-intercept (c) = -3

Hence, the equation of the line is given by

y = m’x + c

y = (5/2) x + (-3)

2y = 5x – 6

5x – 2y – 6 = 0

---

ML Aggarwal Equation of Straight Line Exe-12.2 Class 10 ICSE Maths Solutions

Question -11  

Find the equation of a straight. line perpendicular to the line 3x – 4y + 12 = 0 and having same y-intercept as 2x – y + 5 = 0.

Answer -11

In the given line 3x – 4y + 12 = 0
⇒ 4y = 3x + 12
⇒ y = (3/4) x + 3

Thus, slope (m₁) = ¾

Now, let the slope of the line perpendicular to the given line be taken as m₂

So,

m₁ x m₂ = -1

(3/4) x m₂ = -1

m₂ = -4/3

And given, the y-intercept of the line is same as 2x – y + 5 = 0

⇒ y = 2x + 5

So, the y-intercept is 5 = c.

Hence, the equation of line is given by

y = m₂x + c

y = (-4/3) x + 5

3y = -4x + 15

4x + 3y = 15

Question-12

Find the equation of the line passing through (0, 4) and parallel to the line 3x + 5y + 15 = 0. 

Answer -12

In the given equation 3x + 5y + 15 = 0
⇒ 5y = – 3x – 15
⇒ y  = (-3/5) x – 3

So, slope (m) = -3/5

The slope of the line parallel to the given line will the same -3/5

And, the line passes through the point (0, 4)

Hence, equation of the line will be

y – y₁ = m (x – x₁)

y – 4 = (-3/5) (x – 0)

5y – 20 = -3x

3x + 5y – 20 = 0

Question -13

Write down the equation of the line perpendicular to 3x + 8y = 12 and passing through the point ( – 1, – 2).

Answer -13

In the given line 3x + 8y = 12
⇒ 8y = -3x + 12
⇒ y = (-3/8) x + 12

So, the slope (m₁) = -3/8

Let’s consider the slope of the line perpendicular to the given line as m₂

Then, m₁ x m₂ = -1

-3/8 x m₂ = -1

m₂ = 8/3

Now,

The equation of the line perpendicular to the given line and passing through the point (-1, -2) will be

y – y₁ = m (x – x₁)

y – (-2) = (8/3) (x – (-1))

y + 2 = (8/3) (x + 1)

3y + 6 = 8x + 8

3y = 8x + 2

Thus, the equation of the required line is 3y = 8x + 2.

Question-14  

(i) The line 4x – 3y + 12 = 0 meets the x-axis at A. Write down the co-ordinates of A.
(ii) Determine the equation of the line passing through A and perpendicular to 4x – 3y + 12 = 0.

Answer-14

Given line: 4x – 3y + 12 = 0

(i) When this line meets the x-axis, its y co-ordinate becomes 0.

So, putting y = 0 in the given equation, we get

4x – 3(0) + 12 = 0

4x + 12 = 0

x = -12/4

x = -3

Hence, the line meets the x-axis at A (-3, 0).

(ii) Now, the slope of the line is given by

4x – 3y + 12 = 0

3y = 4x + 12

y = (4/3) x + 4

⇒ m₁ = 4/3

Let’s assume the slope of the line perpendicular to the given line be m₂

Then, m₁ x m₂ = -1

4/3 x m₂ = -1

m₂ = -3/4

Thus, the equation of the line perpendicular to the given line passing through A will be

y – 0 = -3/4 (x + 3)

4y = -3(x + 3)

3x + 4y + 9 = 0

Question -15

Find the equation of the line that is parallel to 2x + 5y – 7 = 0 and passes through the mid-point of the line segment joining the points (2, 7) and ( – 4, 1).

Answer -15

The given line 2x + 5y – 7 = 0
5y = -2x + 7
⇒ y = (-2/5) x + 7/5

So, the slope is -2/5

Hence, the slope of the line that is parallel to the given line will be the same, m = -2/5

Now, the mid-point of the line segment joining points (2, 7) and (– 4, 1) is

((2 – 4)/2, (7 + 1)/2) = (-1, 4)

Thus, the equation of the line will be

y – y₁ = m (x – x₁)

y – 4 = (-2/5) (x + 1)

5y – 20 = -2x -2

2x + 5y = 18

Question -16

Find the equation of the line that is perpendicular to 3x + 2y – 8 = 0 and passes through the mid-point of the line segment joining the points (5, – 2), (2, 2).

Answer -16

In the given line 3x + 2y – 8=0
⇒ 2y = – 3x + 8
so ⇒ y = (-3/2) x + 4

Here, slope (m₁) = -3/2

Now, the co-ordinates of the mid-point of the line segment joining the points (5, -2) and (2, 2) will be

((5 + 2)/7, (-2 + 2)/7) = (7/2, 0)

Let’s consider the slope of the line perpendicular to the given line be m₂

Then,

m₁ x m₂ = -1

(-3/2) x m₂ = -1

m₂ = 2/3

So, the equation of the line with slope m₂ and passing through (7/2, 0) will be

y – 0 = (2/3) (x – 7/2)

3y = 2x – 7

2x – 3y – 7 = 0

Thus, the required line equation is 2x – 3y – 7 = 0.

Question -17  

Find the equation of a straight line passing through the intersection of 2x + 5y – 4 = 0 with x-axis and parallel to the line 3x – 7y + 8 = 0.

Answer -17

Let the point of intersection of the line 2x + 5y – 4 = 0 and x-axis be (x, 0)
Substituting the value of y in the equation
2x + 5 × 0 – 4 = 0
⇒ 2x – 4 = 0
and ⇒ 2x = 4
so ⇒ x = 4/2 = 2
Coordinates of the points of intersection will be (2, 0)

Also given, line equation: 3x – 7y + 8 = 0

7y = 3x + 8

y = (3/7) x + 8/7

So, the slope (m) = 3/7

We know that the slope of any line parallel to the given line will be the same.

So, the equation of the line having slope 3/7 and passing through the point (2, 0) will be

y – 0 = (3/7) (x – 2)

7y = 3x – 6

3x – 7y – 6 = 0

Thus, the required line equation is 3x – 7y – 6 = 0.

Question -18

The equation of a line is 3x + 4y – 7 = 0. Find
(i) the slope of the line. .
(ii) the equation of a line perpendicular to the given line and passing through the intersection of the lines x – y + 2 = 0 and 3x + y – 10 = 0. (2010)

Answer -18

(i) Equation of the line is 3x + 4y – 1 = 0

⇒ 4y = 7 – 3x

y = (-3/4) x + 7

Hence, slope (m₁) = -3/4

(ii) Let the slope of the perpendicular to the given line be m₂

Then, m₁ x m₂ = -1

(-3/4) x m₂ = -1

m₂ = 4/3

Now, to find the point of intersection of

x – y + 2 = 0 … (i)

3x + y – 10 = 0 … (ii)

On adding (i) and (ii), we get

4x – 8 = 0

4x = 8

x = 8/4 = 2

Putting x = 2 in (i), we get

2 – y + 2 = 0

y = 4

Hence, the point of intersection of the lines is (2, 4)

The equation of the line having slope m₂ and passing through (2, 4) will be

y – 4 = (4/3) (x – 2)

3y – 12 = 4x – 8

4x – 3y + 4 = 0

Thus, the required line equation is 4x – 3y + 4 = 0.

Question -19  

Find the equation of the line perpendicular from the point (1, – 2) on the line 4x – 3y – 5 = 0. Also find the co-ordinates of the foot of perpendicular.

Answer -19

In the equation 4x – 3y – 5 = 0,
⇒ 3y = 4x – 5
⇒ y = (4/3) x – 5

Slope of the line (m₁) = 4/3

Let the slope of the line perpendicular to the given line be m₂

Then, m₁ x m₂ = -1

(4/3) x m₂ = -1

m₂ = -3/4

Now, the equation of the line having slope m₂ and passing through the point (1, -2) will be

y + 2 = (-3/4) (x – 1)

4y + 8 = -3x + 3

3x + 4y + 5 = 0

Next, for finding the co-ordinates of the foot of the perpendicular which is the point of intersection of the lines

4x – 3y – 5 = 0 …. (1) and

3x + 4y + 5 = 0 …. (2)

On multiplying (1) by 4 and (2) by 3, we get

16x – 12y – 20 = 0

9x + 12y + 15 = 0

Adding we get,

25x – 5 = 0

x = 5/25

x = 1/5

Putting the value of x in (1), we have

4(1/5) – 3y – 5 = 0

4/5 – 3y – 5 = 0

3y = 4/5 – 5 = (4 – 25)/5

3y = -21/5

y = -7/5

Thus, the co-ordinates are (1/5, -7/5)

Question -20

Prove that the line through (0, 0) and (2, 3) is parallel to the line through (2, – 2) and (6, 4).

Answer -20

Given that
Slope of the line through (0, 0) and (2, 3)

So, m₁ = (y₂ – y₁)/ (x₂ – x₁)

= (3 – 0)/ (2 – 0)

= 3/2

And, let the slope of the line through (2, -2) and (6, 4) be m₂

So, m₂ = (y₂ – y₁)/ (x₂ – x₁)

= (4 + 2)/ (6 – 2)

= 6/4 = 3/2

It’s clearly seen that the slopes m₁ = m₂

Thus, the lines are parallel to each other.

---

ML Aggarwal Equation of Straight Line Exe-12.2 Class 10 ICSE Maths Solutions

Page-246

Question -21

Prove that the line through,( – 2, 6) and (4, 8) is perpendicular to the line through (8, 12) and (4, 24).

Answer -21

Given that
Slope of the line through (-2, 6) and (4, 8)

So, m₁ = (y₂ – y₁)/ (x₂ – x₁)

= (8 – 6)/ (4 + 2)

= 2/6

= 1/3

And, let the slope of the line through (8, 12) and (4, 24) be m₂

So, m₂ = (y₂ – y₁)/ (x₂ – x₁)

= (24 – 12)/ (4 – 8)

= 12/ (-4)

= -3

Now, product of slopes is

m₁ x m₂ = 1/3 x (-3) = -1

Thus, the lines are perpendicular to each other.

Question-22  

Show that the triangle formed by the points A (1, 3), B (3, – 1) and C ( – 5, – 5) is a right angled triangle by using slopes.

Answer -22

Given, points A (1, 3), B (3, – 1) and C (– 5, – 5) form a triangle

Now,

Slope of the line AB = m₁ = (-1 – 3)/ (3 – 1) = -4/2 = -2

And,

Slope of the line BC = m₂ = (-5 + 1)/ (-5 – 3) = -4/-8 = ½

Hence,

m₁ x m₂ = (-2) x (1/2) = -1

So, the lines AB and BC are perpendicular to each other.

Therefore, ∆ABC is a right-angled triangle.

Question -23

Find the equation of the line through the point ( – 1, 3) and parallel to the line joining the points (0, – 2) and (4, 5).

Answer -23

Slope of the line joining the points (0, -2) and (4, 5) = m = (y₂ – y₁) / (x₂ – x₁)
= (5 + 2) / (4 – 0) = 7/4

Slope of the line parallel to it passing through (-1, 3) = 7/4

Hence, the equation of the line is

y – y₁ = m (x – x₁) ⇒ y – 3 = 7/4 (x + 1)

4y – 12 = 7x + 7

7x – 4y + 19 = 0

Question-24

A ( – 1, 3), B (4, 2), C (3, – 2) are the vertices of a triangle.
(i) Find the coordinates of the centroid G of the triangle.
(ii) Find the equation of the line through G and parallel to AC

Answer-24

Given, A (-1, 3), B (4, 2), C (3, -2)
(i) Coordinates of centroid G

G (x, y) = ((x₁ + x₂ + x₃)/2, (y₁+ y₂ + y₃)/2)

= ((-1 + 4 + 3)/3, (3 + 2 – 2)/3)

= (6/3, 3/3) = (2, 1)

Hence, the co-ordinates of the centroid G of the triangle is (2, 1)

(ii) Slope of AC = (y₂ – y₁)/ (x₂ – x₁) = (-2 – 3)/ (3 – (-1)) = -5/4

So, the slope of the line parallel to AC is also -5/4

Now, the equation of line through G is

y – 1 = (-5/4) (x – 2)

4y – 4 = -5x + 10

5x + 4y = 14

Question-25  

Find the equation of the line through (0, – 3) and perpendicular to the line joining the points  (– 3, 2) and (9, 1).

Answer -25

The slope (m₁) of the line joining the points (-3, 2) and (9, 1)

m₁ = (1 – 2)/ (9 + 3) = -1/12

Now, let the slope of the line perpendicular to the above line be m₂

Then, m₁ x m₂ = -1

(-1/12) x m₂ = -1

m₂ = 12

So, the equation of the line passing through (0, -3) and having slope of m₂ will be

y – (-3) = 12 (x – 0)

y + 3 = 12x

12x – y = 3

Thus,

the required line equation is 12x – y = 3.

Question-26

The vertices of a ∆ABC are A(3, 8), B(-1, 2) and C(6, -6). Find :
(i) Slope of BC.
(ii) Equation of a line perpendicular to BC and passing through A.(2019)

Answer-26

Vertices of a ∆ABC are A(3, 8), B(-1, 2) and C(6, -6)

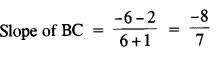
Slope of the line perpendicular to BC = 7/8
Now, equation of the line perpendicular to BC and passing through A is

8y – 64 = 7x – 21
7x – 8y + 43 = 0

Question-27

The vertices of a triangle are A (10, 4), B (4, – 9) and C ( – 2, – 1). Find the equation of the altitude through A. 

(The perpendicular drawn from a vertex of a triangle to the opposite side is called altitude.)

Answer-27

Given, vertices of a triangle are A (10, 4), B (4, – 9) and C (– 2, – 1)

Now,

Slope of line BC (m₁) = (-1 + 9)/ (-2 – 4) = 8/ (-6) = -4/3

Let the slope of the altitude from A (10, 4) to BC be m₂

Then, m₁ x m₂ = -1

(-4/3) x m₂ = -1

m₂ = ¾

So, the equation of the line will be

y – 4 = ¾ (x – 10)

4y – 16 = 3x – 30

3x – 4y – 14 = 0

Question-28  

A (2, – 4), B (3, 3) and C ( – 1, 5) are the vertices of triangle ABC. Find the equation of :
(i) the median of the triangle through A
(ii) the altitude of the triangle through B

Answer -28

(i) D is the mid-point of BC
Co-ordinates of D will

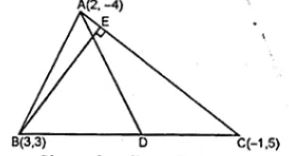
Given, A (2, – 4), B (3, 3) and C (– 1, 5) are the vertices of triangle ABC

(i) D is the mid-point of BC

So, the co-ordinates of D will be

((3 – 1)/2, (3 + 5)/2) = (2/2, 8/2) = (1, 4)

Now,

The slope of AC (m₁) = (5 + 4)/ (-1 – 2) = 9/-3 = -3

Let the slope of BE be m₂

Then, m₁ x m₂ = -1

-3 x m₂ = -1

m₂ = 1/3

so, the equation of BE will be

y – 3 = 1/3 (x – 3)

3y – 9 = x – 3

x – 3y + 6 = 0

Thus, the required line equation is x – 3y + 6 = 0.

Question-29

Find the equation of the right bisector of the line segment joining the points (1, 2) and (5, – 6).

Answer -29

Slope of the line joining the points (1, 2) and (5, -6)

m₁ = (-6 – 2)/ (5 – 1) = -8/4 = -2

Now, if m₂ is the slope of the right bisector of the above line

Then,

m₁ x m₂ = -1

-2 x m₂ = -1

m₂ = ½

The mid-point of the line segment joining (1, 2) and (5, -6) will be

((1 + 5)/2, (2 – 6)/2) = (6/2, -4/2) = (3, -2)

So, equation of the line is

y + 2 = ½ (x – 3)

2y + 4 = x – 3

x – 2y – 7 = 0

Thus, the equation of the required right bisector is x – 2y – 7 = 0.

Question -30  

Points A and B have coordinates (7, – 3) and (1, 9) respectively. Find
(i) the slope of AB.
(ii) the equation of the perpendicular bisector of the line segment AB.
(iii) the value of ‘p’ if ( – 2, p) lies on it.(2008)

Answer -30

Coordinates of A are (7, -3), of B = (1, 9)

(i) The slope of AB (m) = (9 + 3)/ (1 – 7) = 12/ (-6) = -2

(ii) Let PQ be the perpendicular bisector of AB intersecting it at M

Now, the co-ordinates of M will be the mid-point of AB

Co-ordinates of M will be

= (7 + 1)/2, (-3 + 9)/2 = 8/2, 6/2

= (4, 3)

The slope of line PQ will be = -1/m = -1/ (-2) = ½

Thus, the equation of PQ is

y – 3 = ½ (x – 4)

2y – 6 = x – 4

x – 2y + 2 = 0

(iii) As point (-2, p) lies on the above line

The point will satisfy the line equation

-2 – 2p + 2 = 0

-2p = 0

p = 0

Thus, the value of p is 0.

---

ML Aggarwal Equation of Straight Line Exe-12.2 Class 10 ICSE Maths Solutions

Question-31

The points B (1, 3) and D (6, 8) are two opposite vertices of a square ABCD. Find the equation of the diagonal AC.

Answer -31

Given, points B (1, 3) and D (6, 8) are two opposite vertices of a square ABCD

Slope of BD is given by

m₁ = (8 – 3)/ (6 – 1) = 5/5 = 1

We know that, the diagonal AC is a perpendicular bisector of diagonal BD

So, the slope of AC (m₂) will be

m₁ x m₂ = -1

1 x m₂ = -1

m₂ = -1

And, the co-ordinates of mid-point of BD and AC will be

((1 + 6)/2 , (3 + 8)/2) = (7/2, 11/2)

So, the equation of AC is

y – 11/2 = -1 (x – 7/2)

2y – 11 = -2x – 7

2x + 2y – 7 – 11 = 0 ⇒ 2x + 2y – 18 = 0

Thus, the equation of diagonal AC is x + y – 9 = 0.

Question-32

ABCD is a rhombus. The co-ordinates of A and C are (3, 6) and ( – 1, 2) respectively. Write down the equation of BD. (2000)

Answer-32

Given, ABCD is a rhombus and co-ordinates of A are (3, 6) and of C are (-1, 2)

Slope of AC (m₁) = (2 – 6)/ (-1 – 3) = -4/-4 = 1

We know that, the diagonals of a rhombus bisect each other at right angles.

So, the diagonal BD is perpendicular to diagonal AC

Let the slope of BD be m₂

Then, m₁ x m₂ = -1

m₂ = -1/(m₁)

= -1/ (1) = -1

Now, the co-ordinates of the mid-point of AC is given by

((3 – 1)/2, (6 + 2)/2) = (2/2, 8/2) = (1, 4)

So, the equation of BD will be

y – 4 = -1 (x – 1)

y – 4 = -x + 1

x + y = 5

Thus, the equation of BD is x + y = 5.

Question -33  

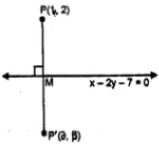
Find the image of the point (1, 2) in the line x – 2y – 7 = 0

Answer -33

Draw a perpendicular from the point P(1, 2) on the line, x – 2y – 7 = 0
Let P’ is the image of P and let its
co-ordinates sue (α, β) slope of line x – 2y – 7 = 0

Given, ABCD is a rhombus and co-ordinates of A are (3, 6) and of C are (-1, 2)

Slope of AC (m₁) = (2 – 6)/ (-1 – 3) = -4/-4 = 1

We know that, the diagonals of a rhombus bisect each other at right angles.

So, the diagonal BD is perpendicular to diagonal AC

Let the slope of BD be m₂

Then, m₁ x m₂ = -1

m₂ = -1/(m₁)

= -1/ (1) = -1

Now, the co-ordinates of the mid-point of AC is given by

((3 – 1)/2, (6 + 2)/2) = (2/2, 8/2) = (1, 4)

So, the equation of BD will be

y – 4 = -1 (x – 1)

y – 4 = -x + 1

x + y = 5

Thus, the equation of BD is x + y = 5.

Question -34

If the line x – 4y – 6 = 0 is the perpendicular bisector of the line segment PQ and the co-ordinates of P are (1, 3), find the co-ordinates of Q.

Answer -34

Given, line equation: x – 4y – 6 = 0 … (i)

Co-ordinates of P are (1, 3)

Let the co-ordinates of Q be (x , y)

Now, the slope of the given line is

4y = x – 6

y = (1/4) x – 6/4

slope (m) = ¼

So, the slope of PQ will be (-1/m) [As the product of slopes of perpendicular lines is -1]

Slope of PQ = -1/ (1/4) = -4

Now, the equation of line PQ will be

y – 3 = (-4) (x – 1)

y – 3 = -4x + 4

4x + y = 7 … (ii)

On solving equations (i) and (ii), we get the coordinates of M

Multiplying (ii) by 4 and adding with (i), we get

x – 4y – 6 = 0

16x + 4y = 28

——————

17x = 34

x = 34/17 = 2

Putting the value of x in (i)

2 – 4y – 6 = 0

-4 – 4y = 0

4y = -4

y = -1

So, the co-ordinates of M are (2, -1)

But, M is the mid-point of line segment PQ

(2, -1) = (x + 1)/2 , (y + 3)/2

(x + 1)/2 = 2

x + 1 = 4

x = 3

And,

(y + 3)/2 = -1

y + 3 = -2

y = -5

Thus, the co-ordinates of Q are (3, -5).

Question -35  

OABC is a square, O is the origin and the points A and B are (3, 0) and (p, q). If OABC lies in the first quadrant, find the values of p and q. Also write down the equations of AB and BC.

Answer -35

—  : End of ML Aggarwal Equation of Straight Line Exe-12.2 Class 10 ICSE Maths : –

Return to – ML Aggarwal Solutions for ICSE Class-10

Thanks

Please Share with Your Friends