ML Aggarwal Coordinate Geometry Exe-19.3 Class 9 ICSE Maths APC Understanding Solutions. Solutions of Exe-19.3. This post is the Solutions of ML Aggarwal Chapter 19 – Coordinate Geometry for ICSE Maths Class-9. APC Understanding ML Aggarwal Solutions (APC) Avichal Publication Solutions of Chapter-19 Coordinate Geometry for ICSE Board Class-9. Visit official website CISCE for detail information about ICSE Board Class-9.
ML Aggarwal Coordinate Geometry Exe-19.3 Class 9 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 9th |
| Chapter-19 | Coordinate Geometry |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-19.3 Questions |
| Edition | 2021-2022 |
Exe-19.3 Solutions of ML Aggarwal for ICSE Class-9 Ch-19, Coordinate Geometry
Note:- Before viewing Solutions of Chapter – 19 Coordinate Geometry Class-9 of ML Aggarwal Solutions . Read the Chapter Carefully. Then solve all example given in Exercise-19.1, Exercise-19.2, Exercise-19.3, Exercise-19.4, MCQs, Chapter Test.
Coordinate Geometry Exercise-19.3
ML Aggarwal Class 9 ICSE Maths Solutions
Page 457
Question 1. Solve the following equations graphically: 3x – 2y = 4, 5x – 2y = 0
Answer :
3x-2y = 4 …(i)
⇒ 2y = 3x-4
⇒ y = (3x-4)/2
When x = 0,
y = (3×0 -4)/2 = (0-4)/2 = -4/2 = -2
when x = 2,
y = (3×2 -4)/2 = (6-4)/2 = 2/2 = 1
when x = 4,
y = (3×4 -4)/2 = (12 -4)/2 = 8/2 = 4
| x | 0 | 2 | 4 |
| y | -2 | 1 | 4 |
Plot the above points on graph. Join them.
5x-2y = 0 …(ii)
⇒ 2y = 5x
⇒ y = 5x/2
When x = 0,
y = 0
When x = 2,
y = 5× 2/2 = 5
When x = -2,
y = 5× -2/2 = -5
| x | 0 | 2 | -2 |
| y | 0 | 5 | -5 |
Plot the above points on graph. Join them.
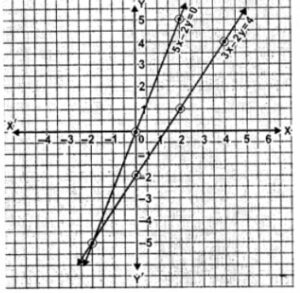
It is clear from the graph that the two lines intersect at (-2,-5).
So the solution of the given equations are x = -2 and y = -5.
Question 2. Solve the following pair of equations graphically. Plot at least 3 points for each straight line 2x – 7y = 6, 5x – 8y = – 4.
Answer :
2x-7y = 6 …(i)
⇒ 2x = 7y+6
⇒ x = (7y+6)/2
when y = 0
x = (7×0 +6)/2 = 6/2 = 3
when y = -1
x = (7×-1 +6)/2 = -1/2 = -0.5
when y = -2
x = (7×-2 +6)/2 = -8/2 = -4
| x | 3 | -0.5 | -4 |
| y | 0 | -1 | -2 |
Mark the above points on graph. Join them.
5x-8y = -4 …(ii)
⇒ 5x = 8y-4
⇒ x = (8y-4)/5
when y = 0
x = (8×0 -4)/5 = -4/5 = 0.8
when y = 3
x = (8×3 -4)/5 = (24-4)/5 = 20/5 = 4
when y = -2
x = (8×-2 -4)/5 = (-16-4)/5 = -20/5 = -4
| x | 0.8 | 4 | -4 |
| y | 0 | 3 | -2 |
Mark the above points on graph. Join them.
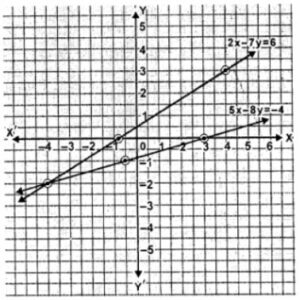
It is clear from the graph that the two lines intersect at (-4,-2).
So the solution of the given equations are x = -4 and y = -2.
Question 3. Using the same axes of co-ordinates and the same unit, solve graphically.
x+y = 0, 3x – 2y = 10
Answer :
x+y = 0 …(i)
⇒ y = -x
When x = -3,
y = 3
When x = -2,
y = 2
When x = -1,
y = 1
| x | -3 | -2 | -1 |
| y | 3 | 2 | 1 |
Mark the above points on graph. Join them.
3x-2y = 10 …(ii)
⇒ 3x = 2y+10
⇒ x = (2y+10)/3
When y = 1
x = (2×1 +10)/3 = 12/3 = 4
When y = -2
x = (2×-2 +10)/3 = 6/3 = 2
When y = 4
x = (2×4 +10)/3 = 18/3 = 6
| x | 4 | 2 | 6 |
| y | 1 | -2 | 4 |
Mark the above points on graph. Join them.
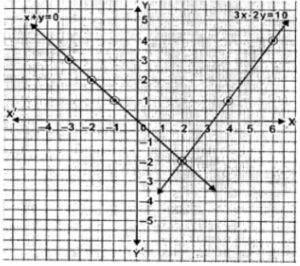
It is clear from the graph that the two lines intersect at (2,-2).
So the solution of the given equations are x = 2 and y = -2.
Question 4. Take 1 cm to represent 1 unit on each axis to draw the graphs of the equations 4x- 5y = -4 and 3x = 2y – 3 on the same graph sheet (same axes). Use your graph to find the solution of the above simultaneous equations.
Answer :
4x-5y = -4 …(i)
⇒ 4x = 5y-4
⇒ x = (5y-4)/4
When y = 0
x = (5×0 -4)/4 = -4/4 = -1
When y = 2
x = (5×2 -4)/4 = 6/4 = 1.5
When y = -2
x = (5×-2 -4)/4 = -14/4 = -3.5
| x | -3.5 | -1 | 1.5 |
| y | -2 | 0 | 2 |
Mark the above points on graph. Join them.
3x = 2y-3 …(ii)
⇒ x = (2y-3)/3
When y = 0,
x = (2×0 -3)/3 = -3/3 = -1
When y = 3,
x = (2×3 -3)/3 = 3/3 = 1
When y = -3,
x = (2×-3-3)/3 = -9/3 = -3
| x | -1 | 1 | -3 |
| y | 0 | 3 | -3 |
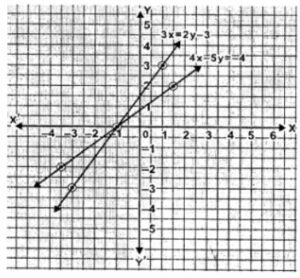
It is clear from the graph that the two lines intersect at (-1,0).
So the solution of the given equations are x = -1 and y = 0.
Question 5. Solve the following simultaneous equations graphically, x + 3y = 8, 3x = 2 + 2y
Answer :
x+3y = 8 …(i)
⇒ 3y = 8-x
⇒ y = (8-x)/3
When x = 8,
y = (8-8)/3 = 0
when x = 2,
y = (8-2)/3 = 6/3 = 2
when x = 5,
y = (8-5)/3 = 3/3 = 1
| x | 2 | 5 | 8 |
| y | 2 | 1 | 0 |
Mark the above points on graph. Join them.
3x = 2+2y
⇒ 2y = 3x-2
⇒ y = (3x-2)/2
When x = 2
y = (3×2 -2)/2 = 4/2 = 2
When x = 4
y = (3×4 -2)/2 = 10/2 = 5
When x = -2
y = (3×-2 -2)/2 = -8/2 = -4
| x | -2 | 2 | 4 |
| y | -4 | 2 | 5 |
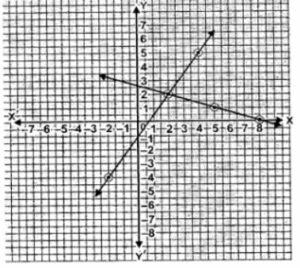
It is clear from the graph that the two lines intersect at (2,2).
So the solution of the given equations are x = 2 and y = 2.
Question 6. Solve graphically the simultaneous equations 3y = 5 – x, 2x = y + 3 (Take 2cm = 1 unit on both axes).
Answer :
3y = 5-x
y = (5-x)/3
When x = 5,
y = (5-5)/3 = 0
When x = 2,
y = (5-2)/3 = 3/3 = 1
When x = -1,
y = (5-(-1))/3 =6/3 = 2
| x | -1 | 2 | 5 |
| y | 2 | 1 | 0 |
Mark the above points on graph. Join them.
2x = y+3 …(ii)
⇒ y = 2x-3
When x = 0,
y = (2×0 -3) = 0-3 = -3
When x = 1,
y = (2×1 -3) = 2-3 = -1
When x = 2,
y = (2×2 -3) = 4-3 = 1
| x | 0 | 1 | 2 |
| y | -3 | -1 | 1 |
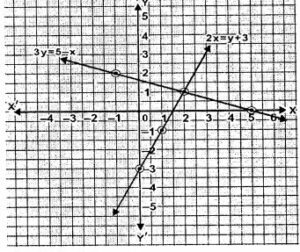
It is clear from the graph that the two lines intersect at (2,1).
So the solution of the given equations are x = 2 and y = 1.
Question 7. Use graph paper for this question.
Take 2 cm = 1 unit on both axes.
(i) Draw the graphs of x +y + 3 = 0 and 3x-2y + 4 = 0. Plot only three points per line.
(ii) Write down the co-ordinates of the point of intersection of the lines.
(iii) Measure and record the distance of the point of intersection of the lines from the origin in cm.

Answer :
(i) x+y+3 = 0 …(i)
⇒ y = -x-3
When x = -3
y = 3-3 = 0
when x = -2
y = 2-3 = -1
when x = -1
y = 1-3 = -2
| x | -1 | -2 | -3 |
| y | -2 | -1 | 0 |
Mark the above points on graph. Join them.
3x-2y+4 = 0 …(ii)
⇒ 2y = 3x+4
⇒ y = (3x+4)/2
When x = -4
y = (3×-4 +4)/2 = (-12+4)/2 = -8/2 = -4
When x = -2
y = (3×-2 +4)/2 = (-6+4)/2 = -2/2 = -1
When x = 2
y = (3×2 +4)/2 = (6+4)/2 = 10/2 = 5
| x | -4 | -2 | 2 |
| y | -4 | -1 | 5 |
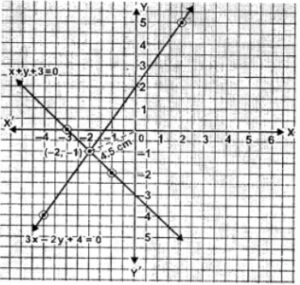
(ii) The two lines intersect at (-2,-1).
(iii) Measure the distance from origin to the point (-2,-1).
The distance of the point of intersection of the lines from the origin is 4.5 cm.
Coordinate Geometry Exercise-19.3
ML Aggarwal Class 9 ICSE Maths Solutions
Page 458
Question 8. Solve the following simultaneous equations, graphically :
2x-3y + 2 = 4x+ 1 = 3x – y + 2
Answer :
2x-3y+2 = 4x+1
⇒ 3y = 2x-4x+2-1
⇒ 3y = -2x+1
⇒ y = (-2x+1)/3
When x = -1,
y = (-2×-1 +1)/3 = 3/3 = 1
When x = 2,
y = (-2×2 +1)/3 = -3/3 = -1
When x = 0.5,
y = (-2×0.5 +1)/3 = 0
| x | 0.5 | 2 | -1 |
| y | 0 | -1 | 1 |
Mark the above points on graph. Join them.
Consider second equation.
4x+1 = 3x-y+2
⇒ y = 3x-4x+2-1
⇒ y = -x+1
When x = 0
y = 0+1 = 1
When x = 1
y = -1+1 = 0
When x = 2
y = -2+1 = -1
| x | 0 | 1 | 2 |
| y | 1 | 0 | -1 |
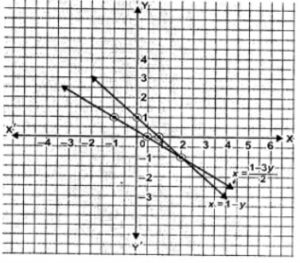
It is clear from the graph that the two lines intersect at (2,-1).
So the solution of the given equations are x = 2 and y = -1.
Question 9. Use graph paper for this question.
(i) Draw the graphs of 3x -y – 2 = 0 and 2x + y – 8 = 0. Take 1 cm = 1 unit on both axes and plot three points per line.
(ii) Write down the co-ordinates of the point of intersection and the area of the traingle formed by the lines and the x-axis.
Answer :
(i) 3x-y-2 = 0 …(i)
y = 3x-2
When x = 0, y = 3×0 -2 = 0-2 = -2
When x = 1, y = 3×1 -2 = 3-2 = 1
When x = 2, y = 3×2 -2 = 6-2 = 4
| x | 0 | 1 | 2 |
| y | -2 | 1 | 4 |
Mark the above points on graph. Join them.
2x+y-8 = 0 …(ii)
y = -2x+8
When x = 1, y = -2×1 +8 = -2+8 = 6
When x = 2, y = -2×2 +8 = -4+8 = 4
When x = 3, y = -2×3 +8 = -6+8 = 2
| x | 1 | 2 | 3 |
| y | 6 | 4 | 2 |
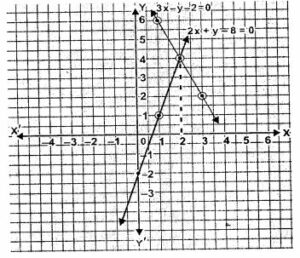
(ii) The coordinates of the points of intersection are (2,4).
Area of the triangle formed = ½ ×base×height
= ½ ×3.4×4
= 6.8 sq. units
Hence,
area of the triangle is 6.8 sq. units.
Question 10. Solve the following system of linear equations graphically : 2x -y – 4 = 0, x + y + 1 = 0. Hence, find the area of the triangle formed by these lines and the y-axis.
Answer :
2x-y-4 = 0 …(i)
y = 2x-4
When x = 1, y = 2×1 -4 = 2-4 = -2
When x = 2, y = 2×2 -4 = 4-4 = 0
When x = 3, y = 2×3 -4 = 6-4 = 2
| x | 1 | 2 | 3 |
| y | -2 | 0 | 2 |
x+y+1 = 0 …(ii)
⇒ y = -x-1
When x = 0, y = 0-1 = -1
When x = -2, y = 2-1 = 1
When x = -1, y = 1-1 = 0
| x | -2 | -1 | 0 |
| y | 1 | 0 | -1 |
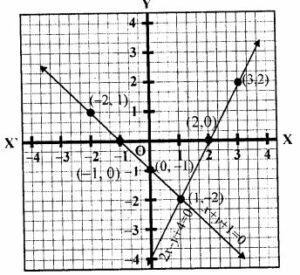
It is clear from the graph that the two lines intersect at (1,-2).
So the solution of the given equations are x = 1 and y = -2.
The area of the triangle formed by these lines and Y axis = ½ × base × height
= ½ ×3×1
= 1.5 sq. units
Hence,
area of the triangle is 1.5 sq. units.
Question 11. Solve graphically the following equations: x + 2y = 4, 3x – 2y = 4
Take 2 cm = 1 unit on each axis. Write down the area of the triangle formed by the lines and the x-axis.
Answer :
x+2y = 4 …(i)
⇒ 2y = 4-x
⇒ y = (4-x)/2
When x = 0, y = (4-0)/2 = 4/2 = 2
When x = 2, y = (4-2)/2 = 2/2 = 1
When x = 4, y = (4-4)/2 = 0/2 = 0
| x | 0 | 2 | 4 |
| y | 2 | 1 | 0 |
3x-2y = 4 …(ii)
⇒ 2y = 3x-4
⇒ y = (3x-4)/2
When x = 0, y = (3×0 -4)/2 = (0-4)/2 = -4/2 = -2
When x = 2, y = (3×2 -4)/2 = (6-4)/2 = 2/2 = 1
When x = 4, y = (3×4 -4)/2 = (12-4)/2 = 8/2 = 4
| x | 0 | 2 | 4 |
| y | -2 | 1 | 4 |

It is clear from the graph that the two lines intersect at (2,1).
So the solution of the given equations are x = 2 and y = 1.
The area of the triangle formed by these lines and X axis = ½ ×base×height
= ½ ×2.7×1
= 1.35 sq. units
Hence area of the triangle is 1.35 sq. units.
Question 12. On graph paper, take 2 cm to represent one unit on both the axes, draw the lines : x + 3 = 0, y – 2 = 0, 2x + 3y = 12 .
Write down the co-ordinates of the vertices of the triangle formed by these lines.
Answer :
x+3 = 0 …(i)
⇒ x = -3
The graph of x = -3 will be a line passing through x = -3 parallel to Y axis.
y-2 = 0 …(ii)
⇒ y = 2
The graph of y = 2 will be a line passing through y = 2 parallel to X axis.
2x+3y = 12 …(iii)
⇒ 3y = 12-2x
⇒ y = (12-2x)/3
When x = 0, y = (12- 2×0)/3 = 12/3 = 4
When x = 3, y = (12- 2×3)/3 = (12-6)/3 = 6/3 = 2
When x = 6, y = (12- 2×6)/3 = (12-12)/3 = 0
| x | 0 | 3 | 6 |
| y | 4 | 2 | 0 |
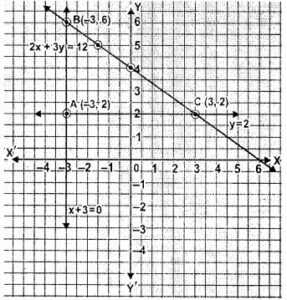
From the graph, it is clear that the vertices of the triangle formed by the lines are A(-3,2), B(-3,6) and C(3,2).
Question 13. Find graphically the co-ordinates of the vertices of the triangle formed by the lines y = 0, y – x and 2x + 3y= 10. Hence find the area of the triangle formed by these lines.
Answer :
y = 0 …(i)
The graph of y = 0 is the X axis.
y = x ..(ii)
When x = 1, y = 1.
When x = 2, y = 2.
When x = 3, y = 3.
| x | 1 | 2 | 3 |
| y | 1 | 2 | 3 |
2x+3y = 10 …(iii)
⇒ 3y = 10-2x
⇒ y = (10-2x)/3
When x = 0.5, y = (10- 2×0.5)/3 = (10-1)/3 = 9/3 = 3
When x = 2, y = (10- 2×2)/3 = (10-4)/3 = 6/3 = 2
When x = 5, y = (10- 2×5)/3 = (10-10)/3 = 0
| x | 0.5 | 2 | 5 |
| y | 3 | 2 | 0 |
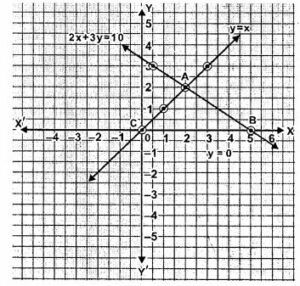
From the graph, it is clear that the vertices of the triangle formed by the lines are A(2,2), B(5,0) and C(0,0).
Area of triangle formed by these lines = ½ × base × height
= ½ ×5×2
= 5 sq. units
Hence, area of the triangle is 5 sq. units.
— : End of ML Aggarwal Coordinate Geometry Exe-19.3 Class 9 ICSE Maths Solutions :–
Return to :- ML Aggarawal Maths Solutions for ICSE Class-9
Thanks
Please Share with Your Friends