ML Aggarwal Coordinate Geometry Exe-19.4 Class 9 ICSE Maths APC Understanding Solutions. Solutions of Exe-19.4. This post is the Solutions of ML Aggarwal Chapter 19 – Coordinate Geometry for ICSE Maths Class-9. APC Understanding ML Aggarwal Solutions (APC) Avichal Publication Solutions of Chapter-19 Coordinate Geometry for ICSE Board Class-9. Visit official website CISCE for detail information about ICSE Board Class-9.
ML Aggarwal Coordinate Geometry Exe-19.4 Class 9 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 9th |
| Chapter-19 | Coordinate Geometry |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-19.4 Questions |
| Edition | 2021-2022 |
Exe-19.4 Solutions of ML Aggarwal for ICSE Class-9 Ch-19, Coordinate Geometry
Note:- Before viewing Solutions of Chapter – 19 Coordinate Geometry Class-9 of ML Aggarwal Solutions . Read the Chapter Carefully. Then solve all example given in Exercise-19.1, Exercise-19.2, Exercise-19.3, Exercise-19.4, MCQs, Chapter Test.
Coordinate Geometry Exercise-19.4
ML Aggarwal Class 9 ICSE Maths Solutions
Page 465
Question 1. Find the distance between the following pairs of points :
(i) (2, 3), (4, 1)
(ii) (0, 0), (36, 15)
(iii) (a, b), (-a, -b)
Answer :
(i) Let P(x1, y1) and Q(x2 , y2) be the
Co-ordinates of P = (2,3)
Co-ordinates of Q = (4,1)
Here x1 = 2, y1 = 3 , x2 = 4, y2 = 1
By distance formula d(P,Q) = √[(x2-x1)2+(y2-y1)2]
d(P,Q) = √[(4-2)2+(1-3)2]
= √[(2)2+(-2)2]
= √(4+4)
= √8
= √(4×2)
= 2√2
distance between P and Q is 2√2 units.
(ii) Let P(x1, y1) and Q(x2 , y2) be the given points
Co-ordinates of P = (0,0)
Co-ordinates of Q = (36,15)
Here x1 = 0, y1 = 0 , x2 = 36, y2 = 15
By distance formula d(P,Q) = √[(x2-x1)2+(y2-y1)2]
d(P,Q) = √[(36-0)2+(15-0)2]
= √[(36)2+(15)2]
= √(1296+225)
= √1521
= 39
distance between P and Q is 39 units.
(iii) Let P(x1, y1) and Q(x2 , y2) be the given points
Co-ordinates of P = (a,b)
Co-ordinates of Q = (-a,-b)
Here x1 = a, y1 = b , x2 = -a, y2 = -b
By distance formula d(P,Q) = √[(x2-x1)2+(y2-y1)2]
d(P,Q) = √[(-a-a)2+(-b-b)2]
= √[(-2a)2+(-2b)2]
= √(4a2+4b2)
= √4(a2+b2)
= 2√(a2+b2)
distance between P and Q is 2√(a2+b2) units.
Question 2. A is a point on y-axis whose ordinate is 4 and B is a point on x-axis whose abscissa is -3. Find the length of the line segment AB.
Answer :
A is a point on Y axis and ordinate is 4.
So the x-coordinate is 0.
coordinates of A are (0,4)
Given B is a point on X axis and abscissa is -3.
So the y-coordinate is 0.
coordinates of B are (-3,0)
By distance formula , Length of AB, d(AB) = √[(x2-x1)2+(y2-y1)2]
d(AB) = √[(-3-0)2+(0-4)2]
= √(-32+-42)
= √(9+16)
= √25
= 5
Hence,
the length of line segment AB is 5 units.
Coordinate Geometry Exercise-19.4
ML Aggarwal Class 9 ICSE Maths Solutions
Page 466
Question 3. Find the value of a, if the distance between the points A (-3, -14) and B (a, -5) is 9 units.
Answer :
Given distance between A(-3,-14) and B(a,-5) is 9 units.
By distance formula , Length of AB, d(AB) = √[(x2-x1)2+(y2-y1)2]
9 = √[(a-(-3))2+(-5-(-14))2]
⇒ 9 = √[(a+3)2+(-5+14)2)]
⇒ 9 = √[(a+3)2+92]
⇒ 9 = √[(a2+6a+9+81)]
⇒ 9 = √[(a2+6a+90)]
81 = a2+6a+90
⇒ a2+6a+90-81 = 0
⇒ a2+6a+9 = 0
⇒ (a+3)(a+3) = 0
⇒ a+3 = 0
⇒ a = -3
Hence,
the value of a is -3.
Question 4.
(i) Find points on the x-axis which are at a distance of 5 units from the point (5, -4).
(ii) Find points on the y-axis are at a distance of 10 units from the point (8, 8) ?
(iii) Find points (or points) which are at a distance of √10 from the point (4, 3) given that the ordinate of the point or points is twice the abscissa.
Answer :
(i) Given the point is on x axis. So y-coordinate is 0.
Let the points on X-axis be A(x,0) which is at a distance of 5 units from B(5,-4).
By distance formula, distance between AB = √[(x2-x1)2+(y2-y1)2]
5 = √[(5-x)2+(-4-0)2]
⇒ 5 = √[(5-x)2+-42]
⇒ 5 = √[(25+x2-10x+16)]
⇒ 5 = √[(x2-10x+41)]
25 = x2-10x+41
⇒ x2-10x+41-25 =0
⇒ x2-10x+16 =0
⇒ (x-2)(x-8) = 0
⇒ x-2 = 0 or x-8 = 0
⇒ x = 2 or x = 8
Hence
the points are (2,0) and (8,0).
(ii) Given the point is on Y axis. So x-coordinate is 0.
Let the points on Y-axis be A(0,y) which is at a distance of 10 units from B(8,8).
By distance formula , distance between AB = √[(x2-x1)2+(y2-y1)2]
10 = √[(8-0)2+(8-y)2]
⇒ 10= √[(8)2+(8-y2]
⇒ 10 = √[(64+64+y2-16y)]
⇒ 10 = √[(y2-16y+128)]
100 = y2-16y+128
⇒ y2-16y+128-100 =0
⇒ y2-16y+28 = 0
⇒ (y-14)(y-2) = 0
⇒ y-14 = 0 or y-2 = 0
⇒ y = 14 or y = 2
Hence the points are (0,14) and (0,2).
(iii) Let the abscissa of the point be x.
Then ordinate = 2x
So the coordinates of the point are (x,2x).
Since the point is at a distance of √10 from the point (4,3),
√[(4-x)2+(3-2x)2] = √10
(4-x)2+(3-2x)2 = 10
⇒ x2+16-8x+4x2 -12x+9-10 = 0
⇒ 5x2-20x+15 = 0
Divide by 5
x2-4x+3 = 0
⇒ (x-3)(x-1) = 0
⇒ x-3 = 0 or x-1 = 0
⇒ x = 3 or x = 1
So 2x = 2×3 = 6 or 2x = 2×1 = 2
Hence,
the points are (3,6) and (1,2).
Question 5. Find the point on the x-axis which, is equidistant from the points (2, -5) and (-2, 9).
Answer :
Let the point on X axis be (x,0) which is equidistant from (2,-5) and (-2,9).
Distance between (x,0) and (2,-5) is equal to the distance between (x,0) and (-2,9).
√[(2-x)2+(-5-0)2] = √[(-2-x)2+(9-0)2] [By distance formula]
⇒ √(4-4x+x2+25) = √(4+4x+x2+81)
⇒ √(x2-4x+29) = √(x2+4x+85)
x2-4x+29 = x2+4x+85
⇒ -4x-4x = 85-29
⇒ -8x = 56
⇒ x = 56/-8
⇒ x = -7
Hence,
the point is (-7,0).
Question 6. Find the value of x such that PQ = QR where the coordinates of P, Q and R are (6, -1), (1, 3) and (x, 8) respectively.
Answer :
Coordinates of P are (6,-1).
Coordinates of Q are (1,3).
Coordinates of R are (x,8).
PQ = QR
By distance formula, √[(1-6)2+(3-(-1))2] = √[(x-1)2+(8-3)2]
⇒ √[(-5)2+(42] = √[(x-1)2+(5)2]
⇒ √[(25+16)] = √[x2-2x+1+25]
⇒ √(41) = √[x2-2x+26]
41= x2-2x+26
⇒ x2-2x+26-41 = 0
⇒ x2-2x+15 = 0
⇒ (x+3)(x-5) = 0
⇒ (x+3)= 0 or (x-5) = 0
x = -3 or x = 5
Hence,
the value of x is -3 or 5.
Question 7. If Q (0, 1) is equidistant from P (5, -3) and R (x, 6) find the values of x.
Answer :
Q(0,1) is equidistant from P(5,-3) and R(x,6).
So PQ = QR
By distance formula, √[(5-0)2+(-3-1))2] = √[(x-0)2+(6-1)2]
√[(5)2+(-42] = √[(x2+(5)2]
⇒ √[(25+16)] = √[x2+25]
⇒ √(41) = √[x2+25]
41 = x2+25
⇒ x2+25-41 = 0
⇒ x2-16= 0
⇒ (x-4)(x+4) = 0
⇒ (x-4) = 0 or (x+4) = 0
⇒ x = 4 or x = -4
Hence,
the value of x is 4 or -4.
Question 8. Find a relation between x and y such that the point (x, y) is equidistant from the points (7, 1) and (3, 5).
Answer :
point (7,1) be Q and the point (3,5) be R.
Let P(x,y) be the point equidistant from Q(7,1) and R(3,5).
So PQ = PR
By distance formula, √[(7-x)2+(1-y))2] = √[(3-x)2+(5-y)2]
⇒ √[x2-14x+49+y2-2y+1] = √[x2-6x+9+y2-10y+25]
⇒ √[x2-14x+y2-2y+50] = √[x2-6x+y2-10y+34]
x2-14x+y2-2y+50 = x2-6x+y2-10y+34
⇒ -14x+6x-2y+10y+50-34 = 0
⇒ -8x+8y+16 = 0
Divide by 8
-x+y+2 = 0
⇒ y = x-2
Hence,
the required relation is y = x-2.
Question 9. The x-coordinate of a point P is twice its y-coordinate. If P is equidistant from the points Q (2, -5) and U (-3, 6), then find the coordinates of P.
Answer :
Let the y co-ordinate be x.
Then x coordinate is 2x.
So coordinates of P are (2x,x).
P is equidistant from the points Q (2, -5) and U (-3, 6).
PQ = PU
By distance formula, √[(2-2x)2+(-5-x))2] = √[(-3-2x)2+(6-x)2]
⇒ √[(4-8x+4x2+25+10x+x2] = √[9+12x+4x2+36-12x+x2]
⇒ √[29+2x+5x2] = √[45+5x2]
29+2x+5x2 = 45+5x2
⇒ 2x+29-45 = 0
⇒ 2x-16 = 0
⇒ 2x = 16
⇒ x = 16/2
⇒ x = 8
So 2x = 2×8 = 16
P(2x,x) = P(16,8)
Hence,
the coordinates of P are (16,8).
Question 10. If the points A (4,3) and B (x, 5) are on a circle with centre C (2, 3), find the value of x.
Answer :
points A(4,3) and B(x,5) are on the circle whose centre is C(2,3).
AC = BC [Radii of same circle]
By distance formula, √[(2-4)2+(3-3)2] = √[(2-x)2+(3-5)2]
⇒ √[(-2)2+0] = √[4-4x+x2+(-2)2]
⇒ √4 = √[4-4x+x2+4]
⇒ √4 = √[8-4x+x2]
⇒ 4 = 8-4x+x2
⇒ x2-4x+4 = 0
⇒ (x-2)(x-2) = 0
⇒ x = 2
Hence,
the value of x is 2.
Question 11. If a point A (0, 2) is equidistant from the points B (3, p) and C (p, 5), then find the value of p.
Answer :
Given A(0,2) is equidistant from B(3,p) and C(p,5)
AB = AC
By distance formula, √[(3-0)2+(p-2)2] = √[(p-0)2+(5-2)2]
⇒ √[(3)2+(p-2)2] = √[(p)2+(3)2]
⇒ √[9+p2-4p+4] = √[p2+9]
⇒ √[p2-4p+13] = √[p2+9]
p2-4p+13 = p2+9
⇒ -4p+13-9 = 0
⇒ -4p+4 = 0
⇒ -4p = -4
p = -4/-4 = 1
Hence,
the value of p is 1.
Question 12. Using distance formula, show that (3, 3) is the centre of the circle passing through the points (6, 2), (0, 4) and (4, 6).
Answer :
Let C(3, 3) is the centre of the circle passing through the points P(6, 2), Q(0, 4) and R(4, 6).
CP = CQ = CR
By distance formula, CP = √[(x2-x1)2+(y2-y1)2]
⇒ CP = √[(6-3)2+(2-3)2]
⇒ CP = √[(3)2+(-1)2]
⇒ CP = √[9+1]
⇒ CP = √10
By distance formula, CQ = √[(x2-x1)2+(y2-y1)2]
⇒ CQ = √[(0-3)2+(4-3)2]
⇒ CQ = √[(3)2+(1)2]
⇒ CQ = √[9+1]
⇒ CQ = √10
By distance formula, CR = √[(x2-x1)2+(y2-y1)2]
⇒ CR = √[(4-3)2+(6-3)2]
⇒ CR = √[(1)2+(3)2]
⇒ CR = √[1+9]
⇒ CR = √10
Since CP = CQ = CR,
C(3,3) is the centre of the circle passing through the points P(6, 2), Q(0, 4) and R(4, 6).
Hence proved.
Question 13. The centre of a circle is C (2α – 1, 3α + 1) and it passes through the point A (-3, -1). If a diameter of the circle is of length 20 units, find the value(s) of α.
Answer :
Centre of a circle is C(2α-1, 3α+1) and it passes through the point A (-3, -1).
Diameter of the circle = 20
radius = 20/2= 10
AC = 10 [radius]
AC = √[(x2-x1)2+(y2-y1)2]
⇒ 10 = √[(2α-1-(-3))2+(3α+1-(-1))2]
⇒ 10 = √[(2α-1+3)2+(3α+1+1)2]
⇒ 10 = √[(2α+2)2+(3α+2)2]
100 = [(2α+2)2+(3α+2)2]
⇒ 100 = 4α2+8α+4+9α2+12α+4
⇒ 100 = 13α2+20α+8
⇒ 13α2+20α+8-100 = 0
⇒ 13α2+20α-92 = 0
⇒ 13α2-26α+46 α -92 = 0
⇒ 13α(α-2)+46(α-2) = 0
⇒ (α-2)( 13α+46) = 0
⇒ α-2 = 0 or 13α+46 = 0
⇒ α = 2 or 13α = -46
⇒ α = 2 or α = -46/13
Hence,
the value is α = 2 or α = -46/13 .
Question 14. Using distance formula, show that the points A (3, 1), B (6, 4) and C (8, 6) are collinear.
Answer :
points are A (3, 1), B (6, 4) and C (8, 6).
If AB+BC = AC, then the three points are collinear.
AB = √[(x2-x1)2+(y2-y1)2]
⇒ AB = √[(6-3)2+(4-1)2]
⇒ AB = √[(3)2+(3)2]
⇒ AB = √[9+9]
⇒ AB = √18
⇒ AB = √(9×2)
⇒ AB = 3√2
BC = √[(x2-x1)2+(y2-y1)2]
⇒ BC = √[(8-6)2+(6-4)2]
⇒ BC = √[(2)2+(2)2]
⇒ BC= √[4+4]
⇒ BC = √8
⇒ BC = √(4×2)
⇒ BC = 2√2
AC = √[(x2-x1)2+(y2-y1)2]
⇒ AC = √[(8-3)2+(6-1)2]
⇒ AC = √[(5)2+(5)2]
⇒ AC= √[25+25]
⇒ AC = √50
⇒ AC = √(25×2)
⇒ AC = 5√2
AB+BC = 3√2+ 2√2 = 5√2 = AC
Hence proved.
So A, B, C are collinear.
Question 15. Check whether the points (5, -2), (6, 4) and (7, -2) are the vertices of an isosceles triangle.
Answer :
Let A( 5, -2), B(6, 4) and C(7, -2) are the vertices of an isosceles triangle.
AB = √[(x2-x1)2+(y2-y1)2]
⇒ AB = √[(6-5)2+(4-(-2))2]
⇒ AB = √[(1)2+(4+2)2]
⇒ AB = √[1+62]
⇒ AB = √(1+36)
⇒ AB = √37
AC = √[(x2-x1)2+(y2-y1)2]
⇒ AC = √[(7-5)2+(-2-(-2))2]
⇒ AC = √[(2)2+(-2+2)2]
⇒ AC= √[4+0]
⇒ AC = √4
⇒ AC = 2
BC = √[(x2-x1)2+(y2-y1)2]
⇒ BC = √[(7-6)2+(-2-4)2]
⇒ BC = √[(1)2+(-6)2]
⇒ BC= √[1+36]
⇒ BC = √37
⇒ BC = √37
Here, AB = BC.
Hence,
ABC is an isosceles triangle.
Question 16. Name the type of triangle formed by the points A (-5, 6), B (-4, -2) and (7, 5).
Answer :
The three vertices of the triangle are A (-5, 6), B (-4, -2) and (7, 5).
AB = √[(x2-x1)2+(y2-y1)2]
⇒ AB = √[(-4-(-5))2+(4-(-2-6))2]
⇒ AB = √[(1)2+(-8)2]
⇒ AB = √[1+64]
⇒ AB = √65
AC = √[(x2-x1)2+(y2-y1)2]
⇒ AC = √[(7-(-5))2+(5-6)2]
⇒ AC = √[(12)2+(-1)2]
⇒ AC= √[144+1]
⇒ AC = √145
BC = √[(x2-x1)2+(y2-y1)2]
⇒ BC = √[(7-(-4))2+(5-(-2))2]
⇒ BC = √[(11)2+(7)2]
⇒ BC= √[121+49]
⇒ BC = √170
Length of all sides of the triangle are different.
ABC is a scalene triangle.
Question 17. Show that the points (1, 1), (- 1, – 1) and (-√3,√3) form an equilateral triangle.
Answer :
Let A(1,1), B(-1,-1) and C(-√3, √3) be the vertices of ABC.
AB = √[(x2-x1)2+(y2-y1)2]
⇒ AB = √[(-1-1)2+(-1-1)2]
⇒ AB = √[(-2)2+(-2)2]
⇒ AB = √[4+4]
⇒ AB = √8
BC = √[(x2-x1)2+(y2-y1)2]
⇒ BC = √[(-√3-(-1))2+(√3-(-1))2]
⇒ BC = √[(-√3+1)2+(√3+1)2]
⇒ BC = √[3-2√3+1+3+2√3+1]
⇒ BC = √8
AC = √[(x2-x1)2+(y2-y1)2]
⇒ AC = √[(-√3-1)2+(√3-1)2]
⇒ AC = √[3+2√3+1+3-2√3+1]
⇒ AC= √8
Here AB = BC = AC.
the points form an equilateral triangle.
Question 18. Show that the points (7, 10), (-2, 5) and (3, -4) are the vertices of an isosceles right triangle.
Answer :
Let A(7,10), B(-2,5) and C(3,-4) be the vertices of ABC.
AB = √[(x2-x1)2+(y2-y1)2]
⇒ AB = √[(-2-7)2+(5-10)2]
⇒ AB = √[(-9)2+(-5)2]
⇒ AB = √[81+25]
⇒ AB = √106
BC = √[(x2-x1)2+(y2-y1)2]
⇒ BC = √[(3-(-2))2+(-4-5)2]
⇒ BC = √[(5)2+(-9)2]
⇒ BC = √(25+81)
⇒ BC = √106
AC = √[(x2-x1)2+(y2-y1)2]
⇒ AC = √[(3-7)2+(-4-10)2]
⇒ AC = √[(-4)2+(-14)2]
⇒ AC= √(16+196)
⇒ AC= √212
Here AB = BC.
ABC is an isosceles triangle.
AB2+BC2 = 106+106
AB2+BC2 = 212 = AC2
So, ABC is a right triangle.
Hence,
ABC is an isosceles right triangle.
Question 19. The points A (0, 3), B (- 2, a) and C (- 1, 4) are the vertices of a right angled triangle at A, find the value of a.
Answer :
Given the points A (0, 3), B (- 2, a) and C (- 1, 4) are the vertices of a right angled triangle at A.
AB = √[(x2-x1)2+(y2-y1)2]
⇒ AB = √[(-2-0)2+(a-3)2]
⇒ AB = √(4+a2-6a+9)
⇒ AB = √( a2-6a+13)
BC = √[(x2-x1)2+(y2-y1)2]
⇒ BC = √[(-1-(-2))2+(4-a)2]
⇒ BC = √[(1)2+16-8a+a2]
⇒ BC = √(17-8a+a2)
⇒ BC = √(a2-8a+17)
AC = √[(x2-x1)2+(y2-y1)2]
⇒ AC = √[(-1-0)2+(4-3)2]
⇒ AC = √[(-1)2+(1)2]
⇒ AC= √(1+1)
⇒ AC= √2
BC2 = AC2 +AB2
⇒ a2-8a+17 = 2+a2-6a+13
⇒ -8a+6a+17-2-13 = 0
⇒ -2a+2 = 0
⇒ 2a = 2
⇒ a = 2/2 = 1
Hence,
the value of a is 1.
Question 20. Show that the points (0, – 1), (- 2, 3), (6, 7) and (8, 3), taken in order, are the vertices of a rectangle. Also find its area.
Answer :
Let the points A(0, – 1), B(- 2, 3), C(6, 7) and D(8, 3) be the vertices of a rectangle.
AB = √[(x2-x1)2+(y2-y1)2]
⇒ AB = √[(-2-0)2+(3-(-1))2]
⇒ AB = √(-2)2+(4)2
⇒ AB = √(4+16)
⇒ AB = √20
⇒ AB = √(4×5)
⇒ AB = 2√5
BC = √[(x2-x1)2+(y2-y1)2]
⇒ BC = √[(6-(-2))2+(7-3)2]
⇒ BC = √[(8)2+42]
⇒ BC = √(64+16)
⇒ BC = √(80)
⇒ BC = √(5×16)
⇒ BC = 4√5
CD = √[(x2-x1)2+(y2-y1)2]
⇒ CD = √[(8-6)2+(3-7)2]
⇒ CD = √[(2)2+(-4)2]
⇒ CD = √(4+16)
⇒ CD = √(20)
⇒ CD = √(4×5)
⇒ CD = 2√5
AD = √[(x2-x1)2+(y2-y1)2]
⇒ AD = √[(8-0)2+(3-(-1))2]
⇒ AD = √[(8)2+(4)2]
⇒ AD = √(64+16)
⇒ AD = √(80)
⇒ AD = √(5×16)
⇒ AD = 4√5
Here AB = CD and BC = AD.
Hence,
these are the vertices of a rectangle.
Area of ▭ABCD = AB × BC
= 2√5 × 4√5
= 40 sq. units.
Hence the area of ▭ABCD is 40 sq. units.
Coordinate Geometry Exercise-19.4
ML Aggarwal Class 9 ICSE Maths Solutions
Page 467
Question 21. If P (2, -1), Q (3, 4), R (-2, 3) and S (-3, -2) be four points in a plane, show that PQRS is a rhombus but not a square. Find the area of the rhombus.
Answer :
P (2, -1), Q (3, 4), R (-2, 3) and S (-3, -2) be four points in a plane.
PQ = √[(x2-x1)2+(y2-y1)2]
⇒ PQ = √[(3-2)2+(4-(-1))2]
⇒ PQ = √(1)2+(5)2
⇒ PQ = √(1+25)
⇒ PQ = √26
QR = √[(x2-x1)2+(y2-y1)2]
⇒ QR = √[(-2-3)2+(3-4)2]
⇒ QR = √[(-5)2+(-1)2]
⇒ QR = √[25+1]
⇒ QR = √26
RS = √[(x2-x1)2+(y2-y1)2]
⇒ RS = √[(-3-(-2))2+(-2-3)2]
⇒ RS = √[(-1)2+(-5)2]
⇒ RS = √[1+25]
⇒ RS = √26
PS = √[(x2-x1)2+(y2-y1)2]
⇒ PS = √[(-3-2)2+(-2-(-1))2]
⇒ PS = √[(-5)2+(-1)2]
⇒ PS = √[25+1]
⇒ PS = √26
Here PQ = QR = RS = PS.
So, it can be a rhombus or a square.
PR = √[(-2-2)2+(3-(-1))2] [Distance formula]
⇒ PR = √[(-4))2+(4)2]
⇒ PR = √(16+16) = √32 = √(16×2) = 4√2
Diagonal, QS = √[(-3-3)2+(-2-4)2] [Distance formula]
⇒ QS = √[(-6))2+(-6)2]
⇒ QS = √[36+36] = √(2×36) = 6√2
Here, diagonals are not equal. So PQRS is not a square. It is a rhombus.
Area of rhombus PQRS = ½ ×PR×QS
= ½ × 4√2×6√2
= 24 sq units.
Hence,
the area of the rhombus PQRS is 24 sq. units.
Question 22. Prove that the points A (2, 3), B {-2, 2), C (-1, -2) aqd D (3, -1) are the vertices of a square ABCD.
Answer :
Let A (2, 3), B (-2, 2), C (-1, -2) and D (3, -1) are the vertices of a square ABCD.
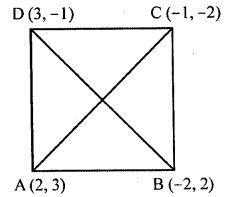
AB = √[(-2-2)2+(2-3)2]
= √[(-4)2+(-1)2]
= √[(16+1)]
= √17
BC = √[(-2-(-1))2+(2-(-2))2]
= √[(-1)2+(4)2]
= √[(1+16)]
= √17
CD = √[(3-(-1))2+(-1-(-2))2]
= √[(4)2+(1)2]
= √[(16+1)]
= √17
AD = √[(3-2)2+(-1-3)2]
= √[(1)2+(-4)2]
= √[(1+16)]
= √17
Here AB = BC = CD = AD.
All the sides are equal .
Diagonal AC = √[(-1-2)2+(-2-3)2]
= √[(-3)2+(-5)2]
= √[9+25]
= √34
Diagonal BD = √[(3-(-2))2+(-1-2)2]
√[(5)2+(-3)2]
= √[(25+9)]
= √34
AC = BD
So,
diagonals are also equal.
Hence,
the points are the vertices of a square.
Question 23. Name the type of quadrilateral formed by the following points and give reasons for your answer :
(i) (-1, -2), (1, 0), (-1, 2), (-3, 0)
(ii) (4, 5), (7, 6), (4, 3), (1, 2)
Answer :
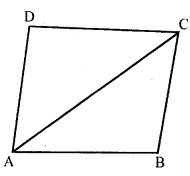
(i) Let A(-1, -2), B(1, 0), C(-1, 2), D(-3, 0)are the given points.
AB = √[(1-(-1))2+(0-(-2))2]
= √[(2)2+(2)2]
= √(4+4)
= √8
BC = √[(-1-1))2+(2-0)2]
= √[(-2)2+(2)2]
= √(4+4)
= √8
CD = √[(-3-(-1))2+(0-2)2]
= √[(-2)2+(-2)2]
= √(4+4)
= √8
AD = √[(-3-(-1))2+(0-(-2))2]
= √[(-2)2+(2)2]
= √(4+4)
= √8
Diagonal AC = √[(-1-(-1))2+(2-(-2))2]
= √[(0)2+(4)2]
= √[16]
= 4
Diagonal BD = √[(-3-1)2+(0-0)2]
√(-4)2+0
= √16
= 4
AC = BD
So, diagonals are also equal.
Also, AB = BC = CD = AD.
All the sides are equal .
Hence,
quadrilateral ABCD is a square.
(ii) Let A(4, 5), B(7, 6), C(4, 3), D(1, 2)are the given points.
AB = √[(7-4)2+(6-5)2]
= √[(3)2+(1)2]
= √(9+1)
= √10
BC = √[(4-7)2+(3-6)2]
= √[(-3)2+(-3)2]
= √(9+9)
= √18
CD = √[(1-4)2+(2-3)2]
= √[(-3)2+(-1)2]
= √(9+1)
= √10
AD = √[(1-4)2+(2-5)2]
= √[(-3)2+(-3)2]
= √(9+9)
= √18
Diagonal AC = √[(4-4)2+(3-5)2]
= √[(0)2+(-2)2]
= √4
= 2
Diagonal BD = √[(1-7)2+(2-6)2]
√(-6)2+-42
= √(36+16)
= √52
AC ≠ BD
AB = CD
BC = AD.
Since, opposite sides are equal and diagonals are not equal, ABCD is a parallelogram.
Question 24. Find the coordinates of the circumcentre of the triangle whose vertices are (8, 6), (8, -2) and (2, -2). Also, find its circumradius.
Answer 24:
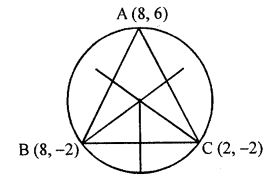
Let O(x,y) be the circumcentre of the circle.
Let A(8, 6), B(8, -2) and C(2, -2) be the vertices of the triangle.
OB = OC [Radii of same circle]
√[(8-x)2+(-2-y)2] = √[(2-x)2+(-2-y)2]
(8-x)2+(-2-y)2 = (2-x)2+(-2-y)2
⇒ 64+x2-16x+4+4y+y2 = 4-4x+x2+4+4y+y2
⇒ 64-16x = 4-4x
⇒ 12x = 60
⇒ x = 60/12 = 5
OA = OB
√[(8-x)2+(6-y)2] = √[(8-x)2+(-2-y)2]
(8-x)2+(6-y)2= (8-x)2+(-2-y)2
⇒ 36-12y+y2 = 4+4y+y2
⇒ -12y-4y = 4-36
⇒ -16y = -32
⇒ y = 32/16 = 2
Hence,
the coordinates of O are (5,2).
OA = √[(8-5)2+(6-2)2]
= √[(3)2+(4)2]
= √[9+16]
= √25 = 5
Hence the circumradius is 5 units.
— : End of ML Aggarwal Coordinate Geometry Exe-19.4 Class 9 ICSE Maths Solutions :–
Return to :- ML Aggarawal Maths Solutions for ICSE Class-9
Thanks
Please Share with Your Friends