ML Aggarwal Triangles Exe-10.3 for ICSE Class 9 Maths Solutions

ML Aggarwal Triangles Exe-10.3 for ICSE Class 9 Maths Solutions Ch-10. Step by Step Answer of Exe-10.3 of Triangles of ML Aggarwal for ICSE Class 9th Mathematics Questions. Visit official website CISCE for detail information about ICSE Board Class-9.

ML Aggarwal Triangles Exe-10.3 for ICSE Class 9 Maths Solutions Ch-10

Board	ICSE
Subject	Maths
Class	9th
Chapter-10	Triangles
Topics	Solution of Exe-10.3 Questions
Academic Session	2024-2025

Solution of Exe-10.3 Questions

ML Aggarwal Triangles Exe-10.3 for ICSE Class 9 Maths Solutions Ch-10

Question 1. ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.

Answer : In right angled triangle ABC, ∠A = 90^o

∠B + ∠C

= 180^o – ∠A

= 180^o – 90^o = 90^o

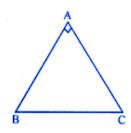
Because AB = AC

∠C = ∠B (Angles opposite to equal sides)

∠B + ∠B = 90^o 

(2∠B = 90^o)

⇒ ∠B = 90/2^o = 45^o

⇒ ∠B = ∠C = 45^o

⇒ ∠B = ∠C = 45^o 

Question 2. Show that the angles of an equilateral triangle are 60° each.

Answer : ∆ABC is an equilateral triangle

AB = BC = CA

∠A = ∠B = ∠C (opposite to equal sides )

But ∠A + ∠B + ∠C = 180^o (sum of angles of a triangle)

3∠A = 180^o (∠A = 180^o/3 = 60^o)

⇒ ∠A = ∠B = ∠C = 60^o

Question 3. Show that every equiangular triangle is equilateral.

Answer : ∆ABC is an equiangular

∠A = ∠B = ∠C

In ∆ABC

∠B = ∠C …(i)

AC = AB …(ii) (sides opposite to equal angles)

∠C = ∠A

BC = AB

From (i) and (ii)

AB = BC = AC

∆ABC is an equilateral triangle

Question 4.  In the following diagrams, find the value of x:

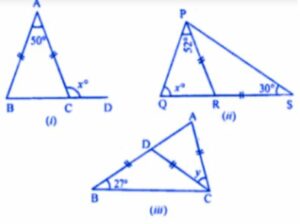
Answer : (i) In following diagram given that AB =AC

That is ∠B = ∠ ACB (angles opposite to equal sides in a triangle are equal)

In a triangle are equal)

Now, ∠A + ∠B + ∠ACB = 180^o (sum of all angles in a triangle is 180^o)

50 + ∠B + ∠B = 180^o(∠A = 50^o (given) ∠B = ∠ACB)

⇒ 50^o + 2 ∠B = 180^o (2∠B = 180^o – 50^o)

⇒ 2∠B = 130^o (∠B = 130/2 = 65^o)

⇒ ∠ACB = 65^o

Also ∠ACB + x^o = 180^o (Linear pair)

⇒ 65^o + x^o = 180^o (x^o = 180^o – 65^o)

⇒ x^o = 115^o

Hence, Value of x = 115

(ii) in ∆PRS,

Given that PR = RS

∠PSR = ∠RPS (Angles opposite in a triangle, equal sides are equal)

30^o = ∠RPS …(i) (∠PPS = 30^o)

⇒ ∠QPS = ∠QPR + ∠RPS

⇒ ∠QPS = 52^o + 30^o (Given, ∠QPR = 52^o and from (i), ∠RPS = 30^o)

⇒ ∠QPS = 82^o

Now, In ∆PQS

∠QPS + ∠QSP + PQS = 180^o (sum of all angles in a triangles is 180^o)

= 82^o + 30^o + x^o = 180^o (from (2) ∠QPS = 82^o and ∠QSP = 30^o (given)

⇒ 112^o + x^o = 180^o (x^o = 180^o – 112^o)

Hence, Value of x = 68

(iii) In the following figure, Given

That, BD = CD = AC and ∠DBC = 27^o

Now in ∆BCD,

BD = CD (Given)

⇒ ∠DBC = ∠BCD …(1) (in a triangle sides opposite equal angles are equal)

Also,, ∠DBC = 27^o ….(2) (given)

From (1) and (2) we get

∠BCD = 27^o

Now,

∠CDA = ∠DBC + ∠BCD (exterior angles is equal to sum of two interior opposite angles)

Ext ∠CDA = 27^o + 27^o [from (2) and (3)]

∠CDA = 54^o

Also, in ∆ACD

∠CAD + ∠CDA + ∠ACD = 180^o (sum of all angles in a triangle is 180^o)

⇒ 54^o + 54^o+ Y = 180^o

⇒ 108^o + Y = 180^o (Y = 180^o – 108^o)

⇒ y = 72^o

Question 5. In the following diagrams, find the value of x:

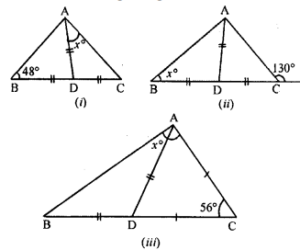
Answer : 

Question 6.

(a) In the figure (1) given below, AB = AD, BC = DC. Find ∠ ABC.
(b)In the figure (2) given below, BC = CD. Find ∠ACB.
(c) In the figure (3) given below, AB || CD and CA = CE. If ∠ACE = 74° and ∠BAE =15°, find the values of x and y.

Answer :  Update soon..

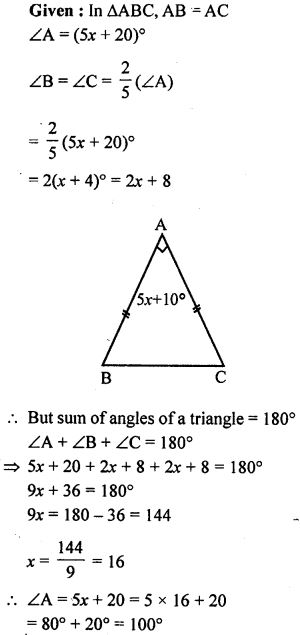
Question 7. In ∆ABC, AB = AC, ∠A = (5x + 20)° and each of the base angle is 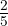 the of ∠A. Find the measure of ∠A.

Answer :

Question 8.  (a) In the figure (1) given below, ABC is an equilateral triangle. Base BC is produced to E, such that BC’= CE. Calculate ∠ACE and ∠AEC.

(b) In the figure (2) given below, prove that ∠ BAD : ∠ ADB = 3 : 1.
(c) In the figure (3) given below, AB || CD. Find the values of x, y and ∠.

Answer : (a) in following figure

Given,

ABC is an equilateral triangle BC = CE

To find: ∠ACE and ∠AEC

As given that ABC is an equilateral triangle,

That is ∠BAC = ∠B = ∠ACB = 60^o …(1) (each angle of an equilateral triangle is 60^o)

Now, ∠ACE = ∠BAC + CB (Exterior angle is equal to sum of two interior opposite angles) (∠ACE = 60^o + 60^o)

∠ACE = 120⁰

Then, in ∆ACE

Given, AC = CE [because AC = BC = CE]

∠CAE = ∠AEC …(2)

We know that, in a triangle equal sides have equal angles opposite to them.

So, ∠CAE + ∠AEC + 120^o = 80^o

⇒ ∠AEC + ∠AEC + 120^o = 180^o [by equation (2) we get]

⇒ 2∠AEC = 180^o – 120^o

⇒ 2∠AEC = 60^o

⇒ ∠AEC = 60^o/2

⇒ ∠AEC = 30^o

Therefore, ∠ACE = 120^o and ∠AEC = 30^o.

(b) In given figure,

Given, ∆ABD, AC meets BD in C. AB = BC, AC = CD.

We have to prove that, ∠BAD : ∠ADB = 3: 1

Then, consider ∆ABC,

AB = BC [given]

Therefore, ∠ACB = ∠BAC …(1) (In a triangle, equal angles opposite to them)

In ∆ACD,

AC = CD [given]

Therefore, ∠ADC = ∠CAD (In a triangle, equal sides have equal angles opposite to them)

∠CAD = ∠ADC …(2)

From, adding (1) and (2), we get

∠BAC + ∠CAD = ∠ACB + ∠ADC

⇒ ∠BAD = ∠ACB + ∠ADC …(3)

Now, in ∆ACD

Exterior ∠ACB = ∠CAD + ∠ADC …(4) (In an triangle, exterior angle is equal to sum of two interior opposite angles)

Therefore, ∠ACB = ∠ADC + ∠ADC [from (2) and (4)]

∠ACB = 2∠ADC …(5)

Now, ∠BAD = 2∠ADC + ∠ADC [from (3) and (4)]

⇒ ∠BAD = 3∠ADC = (∠BAD/∠ADC) = 3/1

⇒ ∠BAD: ∠ADC = 3: 1

(c) In given figure,

Given, AB parallel to CD, ∠ECD = 24^o, ∠CDE = 42^o

We have to find the value of x, y and z.

Consider, ∆CDE

Exterior, ∠CEA = 24^o + 42^o (In a triangle exterior angle is equal to sum of two interior opposite angles)

∠CEA = 66^o …(1)

Then, in ∆ACE

AC = CE (given)

Therefore, ∠CAE = ∠CEA (In a triangle equal side have equal angles opposite to them)

By equation (1),

Y = 66^o …(2)

Also, y + z + ∠CEA = 180^o

We know that, sum of all angles in a triangle is 180^o

66^o + z + 66^o = 180^o

⇒ z + 132^o = 180^o

⇒ z = 180^o – 132^o

⇒ z = 48^o …(3)

Then it is given that, AB is parallel to CD,

∠x = ∠ADC [alternate angles]

⇒ x = 42^o …(4)

Hence, from (2), (3) and (4) equation gives x = 42^o, y = 66^o and z = 48^o.

Question 9. In the given figure, D is mid-point of BC, DE and DF are perpendiculars to AB and AC respectively such that DE = DF. Prove that ABC is an isosceles triangle.

Answer :  D is the midpoint of BC

DE perpendicular to AB

And DF perpendicular to AC

DE = DE

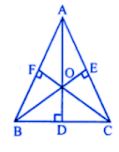
To prove:

Triangle ABC is an isosceles triangle

Proof:

In the right angled triangle BED and CDF

Hypotenuse BD = DC (because D is a midpoint)

Side DF = DE (given)

∆BED ≅ ∆CDF (RHS axiom)

∠C = ∠B

AB = AC (sides opposite to equal angles)

∆ABC is an isosceles triangle

Question 10. In the given figure, AD, BE and CF arc altitudes of ∆ABC. If AD = BE = CF, prove that ABC is an equilateral triangle.

Answer : AD, BE and CF are altitudes of ∆ABC and

AD = BE = CF

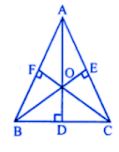
To prove : ∆ABC is an equilateral triangle

Proof: in the right ∆BEC and ∆BFC

Hypotenuse BC = BC (Common)

Side BE = CF (Given)

∆BEC ≅ ∆BFC (RHS axiom)

∠C = ∠B

AB = AC (sides opposite to equal angles)

Similarly we can prove that ∆CFA ≅ ∆ADC

∠A = ∠C

AB = BC

From (i) and (ii)

AB = BC = AC

∆ABC is an equilateral triangle

Question 11. In a triangle ABC, AB = AC, D and E are points on the sides AB and AC respectively such that BD = CE. Show that:

(i) ∆DBC ≅ ∆ECB
(ii) ∠DCB = ∠EBC
(iii) OB = OC, where O is the point of intersection of BE and CD.

Answer: 

 

Question 12. ABC is an isosceles triangle in which AB = AC. P is any point in the interior of ∆ABC such that ∠ABP = ∠ACP. Prove that

(a) BP = CP
(b) AP bisects ∠BAC.

Answer : (a)  

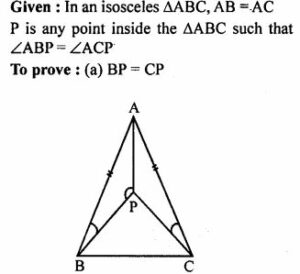
Proof:

In  tr. APB and tr. APC,

AB = AC [given]

∠ ABP = ∠ ACP [given]

AP = AP [common]

So Tr ABP and Tr ACP are congruent  by (SSA)

So BP = PC   c.p.c.t.

(b) To Prove: AP bisects angle BAC

angle PAB = angle PAC [corresponding angles of congruent triangles]

thus, AP bisects angle BAC.

hence proved.

Question 13. In the adjoining figure, D and E are points on the side BC of ∆ABC such that BD = EC and AD = AE. Show that ∆ABD ≅ ∆ACE.

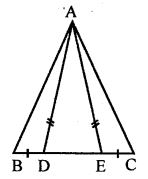
Answer :

Point D and E are on side BC of ∆ABC,

such that BD = CE ,and AD = AE .

To prove : ∆ABD congruent to ∆ACE

proof :

(i) In ∆ADE ,

AD = AE ( given )

∠ADE = ∠AED = x

[ Angles opposite to equal sides ]

ii ) ∠ADB + ∠ADC= 180°

[ Linear pair ]

∠ADB + x = 180°

∠ADB = 180° – x —–( 1 )

(iii) Similarly ,

∠AEC = 180° – x ——–( 2 )

(iv) In ∆ABD and ∆ACE ,

BD = EC ( S ) given ,

∠ADE = ∠AEC ( A ) from ( 1 ) and ( 2 )]

AD = AE ( S ) given ,

Hence ,

∆ABD is congruent to ∆ACE.

[ ASA congruence Rule ]

Question 14.

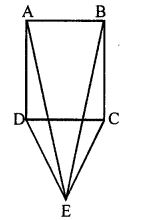
(a) In the figure (i) given below, CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ∆ADE ≅ ∆BCE and hence, AEB is an isosceles triangle.

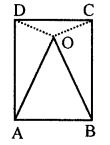
(b) In the figure (ii) given below, O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that OCD is an isosceles triangle.

Answer:- 

Question 15.  In the given figure, ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.

Answer :

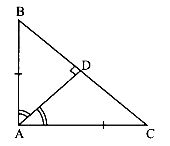
In ∆ABD and ∆ACD

AB = AC (given)

∠BAD = ∠CAD

As AD is bisector of ∠A and AD = AD

⇒ ∆DAB = ∆DAC (by SAS congruency rule)

⇒ ∠ADB = ∠ADC (by c.p.c.t)

⇒ ∠ADB = ∠ADC = 90°

and BD = DC

In ∆ABD,

AD2 + BD2 = AB2 …(i)

⇒ AD2 + DC2 = AC2 …(ii)

Adding (i) and (ii), we get

2 AD2 + BD2 + DC2 = AB2 + AC2

⇒ 2AD2 + BD2 + DC2 = BC2

⇒ 2 AD2 + 2BD2 = BC2

⇒ 2 (AD2 + BD2) = BC2

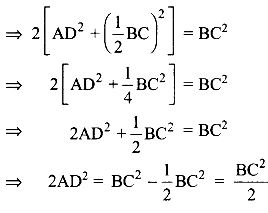
⇒ 4 AD2 = BC2

⇒ 2 AD = BC

i.e. BC = 2AD

Hence proved.

—  : End of ML Aggarwal Triangles Exe-10.3 for ICSE Class 9 Maths Solutions Ch-10 :–

Return to :-  ML Aggarawal Maths Solutions for ICSE  Class-9

Thanks

Please Share with Your Friends