ML Aggarwal Mensuration Exe-16.2 Class 9 ICSE Maths Solutions Ch-16. Step by Step Solutions of 16.2 Questions on Mensuration of ML Aggarwal for ICSE Class 9th Mathematics. Visit official website CISCE for detail information about ICSE Board Class-9.
ML Aggarwal Mensuration Exe-16.2 Class 9 ICSE Maths Solutions
| Board | ICSE |
| Subject | Maths |
| Class | 9th |
| Chapter-16 | Mensuration |
| Topics | Solution of Exe-16.2 Questions |
| Academic Session | 2024-2025 |
Solution of Exe-16.2 Questions on Mensuration
ML Aggarwal Class 9 ICSE Maths Solutions Ch-16.
Question 1.
(i) Find the area of quadrilateral whose one diagonal is 20 cm long and the perpendiculars to this diagonal from other vertices are of length 9 cm and 15 cm.
(ii) Find the area of quadrilateral whose diagonal are 18 cm and 12 cm and they intersect each other at right angle.
Answer :
(i) Consider ABCD as a quadrilateral in which AC = 20 cm
We know that, BY = 9 cm and DY = 15 cm

Here
Area of quadrilateral ABCD = Area of triangle ABC + Area of triangle ACD
We can write it as
= ½ × base × height + ½ × base × height
So we get
= (½ ×AC×BX) + (½ ×AC×DY)
= (½ × 20 × 9) + (½ × 20 × 15)
By further calculation
= (10×9) + (10×15)
= 90 + 150
= 240 cm2
(ii) Consider ABCD as a quadrilateral in which the diagonals AC and BD intersect each other at M at right angles
AC = 18 cm and BD = 12 cm
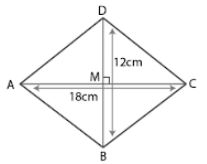
We know that, Area of quadrilateral ABCD = ½ ×diagonal AC ×diagonal BD
= ½ ×18×12
By calculation
= 9×12
= 108 cm2
Question 2. Find the area of the quadrilateral field ABCD whose sides AB = 40 m, BC = 28 m, CD = 15 m, AD = 9 m and ∠A = 90°
Answer :
ABCD is a quadrilateral field
AB = 40 m, BC = 28 m, CD = 15 m, AD = 9 m and ∠A = 90°
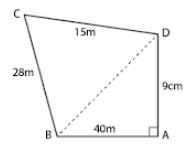
In triangle BAD
∠A = 900
Using the Pythagoras Theorem
BD2 = BA2 + AD2
BD2 = 402 + 92
By calculation
BD2 = 1600 + 81 = 1681
So ,
BD = 41
We know that, Area of quadrilateral ABCD = Area of △BAD + Area of △BDC
It can be written as
= ½ × base × height + Area of △BDC
= ½ × 40 × 9 + Area of △BDC
By calculation
= 180 m2 + Area of △BDC
Determining the area of △BDC
Consider a = BD = 41 m, b = CD = 15 m, c = BC = 28 m
S = Semi perimeter = (a + b + c)/2
= (41 + 15 + 28)/2
= 42 cm
Here,
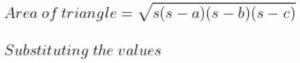
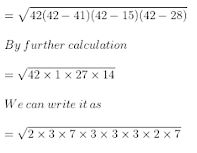
= 2×7×3×3
= 126 m2
So, the area of quadrilateral ABCD = 180 m2 + Area of △BDC
= 180 + 126
= 306 m2
Question 3. Find the area of the quadrilateral ABCD in which ∠BCA= 90°, AB = 13 cm and ACD is an equilateral triangle of side 12 cm.

Answer :
ABCD is a quadrilateral in which ∠BCA = 90° and AB = 13 cm
ABCD is an equilateral triangle in which AC = CD = AD = 12 cm
In right angled △ABC
Using Pythagoras theorem,
AB2 = AC2 + BC2
132 = 122 + BC2
By calculation
BC2 = 132 – 122
⇒ BC2 = 169 – 144 = 25
BC = √25 = 5 cm
Area of quadrilateral ABCD = Area of △ABC + Area of △ACD
It can be written,
= (½ ×base× height) + (√3/4 × side2)
= (½ ×AC×BC) + (√3/4 × 122)
= (½ ×12×5) + (√3/4 × 12 × 12)
So we get
= (6 × 5) + (√3 × 3 × 12)
= 30 + 36√3
Substituting the value of √3
= 30 + (36 × 1.732)
= 30 + 62.28
= 92.28 cm2
(ML Aggarwal Mensuration Exe-16.2 Class 9 ICSE Maths Solutions)
Question 4. Find the area of quadrilateral ABCD in which ∠B = 90°, AB = 6 cm, BC = 8 cm 13 and CD = AD = 13 cm.

Answer :
ABCD is a quadrilateral in which ∠B = 90°, AB = 6 cm, BC = 8 cm and CD = AD = 13 cm
In △ABC
Using Pythagoras theorem
AC2 = AB2 + BC2
AC2 = 62 + 82
By calculation
AC2 = 36 + 64 = 100
AC2 = 102
⇒ AC = 10 cm
Area of quadrilateral ABCD = Area of △ABC + Area of △ACD
It can be written as
= ½ × base × height + Area of △ACD
= ½ × AB × BC + Area of △ACD
= ½ × 6 × 8 + Area of △ACD
By calculation
= 24 cm2 + Area of △ACD …(1)
Finding the area of △ACD
Consider a = AC = 10 cm, b = CD = 13 cm, c = AD = 13 cm
We know that, S = Semi perimeter = (a + b + c)/2
Substituting the values
= (10 + 13 + 13)/ 2
= (10 + 26)/2
= 36/2
= 18 cm
Here,
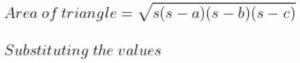

= 3 × 2 × 2 × 5
= 60 cm2
Using equation (1)
Area of quadrilateral ABCD = 24 cm2 + Area of △ACD
= 24 + 60
= 84 cm2
Question 5. The perimeter of a rectangular cardboard is 96 cm ; If its breadth is 18 cm, find the length and the area of the cardboard.
Answer :
Consider ABCD as a rectangle
Take length = l cm
Breadth = 18 cm
Perimeter = 96 cm
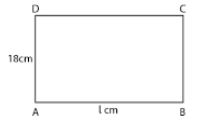
2 × (l + b) = 96 cm
2 × (l + 18) = 96 cm
By calculation
(l + 18) = 96/2
⇒ l + 18 = 48
So we get
⇒ l = 48 – 18 = 30 cm
Here,
Area of rectangular cardboard = l × b
= 30 × 18
= 540 cm2
Question 6. The length of a rectangular hall is 5 m more than its breadth, If the area of the hall is 594 m2, find its perimeter.

Answer :
Let ABCD be rectangular field.
Take Breadth = x m
Length = (x + 5) m
Area of rectangular field = l × b
594 = x (x + 5)
By calculation
594 = x2 + 5x
⇒ 0 = x2 + 5x – 594
⇒ x2 + 5x – 594 = 0
It can be written as
x2 + 27x – 22x – 594 = 0
Taking out the common terms
x (x + 27) – 22 (x + 27) = 0
So,
(x – 22) (x + 27) = 0
Here,
x – 22 = 0 or x + 27 = 0
We get,
x = 22 m or x = -27 which is not possible
Breadth = 22 m
Length = (x + 5) = 22 + 5 = 27 m
Perimeter = 2 (l + b)
= 2 (27 + 22)
By further calculation
= 2 × 49
= 98 m
Question 7.
(a) The diagram (i) given below shows two paths drawn inside a rectangular field 50 m long and 35 m wide. The width of each path is 5 metres. Find the area of the shaded portion.
(b) In the diagram (ii) given below, calculate the area of the shaded portion. All measurements are in centimetres.

Answer :
(a) Area of shaded portion = Area of rectangle ABCD + Area of rectangle PQRS – Area of square LMNO
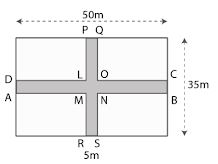
= (50×5) + (5×35) – (5×5)
By calculation
= 250 + 175 – 25
So ,
= 250 + 150
= 400 m2
(b) Area of shaded portion = Area of ABCD – 5 × Area of any small square
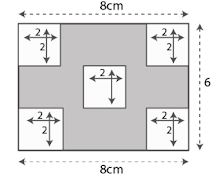
It can be written as
= (l×b) – (5×side×side)
= (8×6) – (5×2×2)
By further calculation
= 48 – 20
= 28 cm2
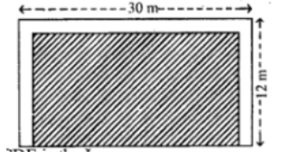
Question 8. A rectangular plot 20 m long and 14 m wide is to be covered with grass leaving 2 m all around. Find the area to be laid with grass.
Answer :
Consider ABCD as a plot
Length of plot = 20 m
Breadth of plot = 14 m
Take PQRS as the grassy plot
Here,
Length of grassy lawn = 20 – 2×2
By calculation
= 20 – 4
= 16 m
Breadth of grassy lawn = 14 – 2×2
By calculation
= 14 – 4
= 10 m
Area of grassy lawn = length × breadth
= 16 × 10
= 160 m2
(ML Aggarwal Mensuration Exe-16.2 Class 9 ICSE Maths Solutions)
Question 9. The shaded region of the given diagram represents the lawn in front of a house. On three sides of the lawn there are flower beds of width 2 m.
(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower – beds.
Answer :
BCDE is the lawn
(i) We know that
Length of lawn BCDE = BC
It can be written as
= AD – AB – CD
= 30 – 2 – 2
By calculation
= 30 – 4
= 26 m
Breadth of lawn BDCE = BE
It can be written as
= AG – GH
= 12 – 2
= 10 m
(ii) We know that, Area of flower beds = Area of rectangle ADFG – Area of lawn BCDE
It can be written as
= (AD×AG) – (BC×BE)
= (30×12) – (26×10)
By calculation
= 360 – 260
= 100 m2
Mensuration Exercise-16.2
ML Aggarwal Class 9 ICSE Maths Solutions
Page 364
Question 10. A foot path of uniform width runs all around the inside of a rectangular field 50 m long and 38m wide. If the area of the path is 492 m². Find its width.
Answer :
ABCD as a rectangular field having
Length = 50 m
Breadth = 38 m
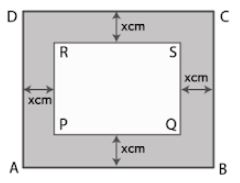
We know that, Area of rectangular field ABCD = l × b
= 50 × 38
= 1900 m2
Let x m as the width of foot path all around the inside of a rectangular field
Length of rectangular field PQRS = (50 – x – x) = (50 – 2x) m
Breadth of rectangular field PQRS = (38 – x – x) = (38 – 2x) m
Here,
Area of foot path = Area of rectangular field ABCD – Area of rectangular field PQRS
492 = 1900 – (50 – 2x) (38 – 2x)
It can be written as
492 = 1900 – [50(38 – 2x) – 2x(38 – 2x)]
By calculation
492 = 1900 – (1900 – 100x – 76x + 4x2)
⇒ 492 = 1900 – 1900 + 100x + 76x – 4x2
On further simplification
492 = 176x – 4x2
Taking out 4 as common
492 = 4 (44x – x2)
⇒ 44x – x2 = 492/4 = 123
We get
x2 – 44x + 123 = 0
It can be written as
x2 – 41x – 3x + 123 = 0
Taking out the common terms
x (x – 41) – 3 (x – 41) = 0
⇒ (x – 3) (x – 41) = 0
Here
x – 3 = 0 or x – 41 = 0
So, x = 3 m or x = 41 m which is not possible
Hence, width is 3 m.
(ML Aggarwal Mensuration Exe-16.2 Class 9 ICSE Maths Solutions)
Question 11. The cost of enclosing a rectangular garden with a fence all around at the rate of Rs. 15 per metre is Rs. 5400. If the length of the garden is 100 m And the area of the garden.
Answer :
ABCD as a rectangular garden
Length = 100 m
Take breadth = x m
Perimeter of the garden = 2 (l + b)
= 2 (100 + x)
= (200 + 2x) m
We know that, Cost of 1 m to enclosing a rectangular garden = Rs 15
So the cost of (200 + 2x) m to enclosing a rectangular garden = 15 (200 + 2x)
= 3000 + 30x
Given cost = Rs 5400
We get,
3000 + 30x = 5400
It can be written as
30x = 5400 – 3000
x = 2400/30 = 80 m
Breadth of garden = 80 m
So the area of rectangular field = l × b
= 100 × 80
= 8000 m2
Question 12. A rectangular floor which measures 15 m x 8 m is to be laid with tiles measuring 50 cm x 25 cm find the number of tiles required further, if a carpet is laid on the floor so that a space of 1 m exists between its edges and the edges of the floor, what fraction of the floor is uncovered?
Answer :
ABCD as a rectangular field of measurement 15m × 8m
Length = 15 m
Breadth = 8 m

Here the area = l × b = 15 × 8 = 120 m2
Measurement of tiles = 50 cm × 25 cm
Length = 50 cm = 50/100 = ½ m
Breadth = 25 cm = 25/100 = ¼ m
So, the area of one tile = ½ × ¼ = 1/8 m2
No. of required tiles = Area of rectangular field/Area of one tile
= 120/(1/8)
By calculation
= (120 × 8)/1
= 960 tiles
Length of carpet = 15 – 1 – 1
= 15 – 2
= 13 m
Breadth of carpet = 8 – 1 – 1
= 8 – 2
= 6 m
Area of carpet = l × b
= 13 × 6
= 78 m2
We know that, Area of floor which is uncovered by carpet = Area of floor – Area of carpet
= 120 – 78
= 42 m2
Fraction = Area of floor which is uncovered by carpet/ Area of floor
= 42/120
= 7/20
Question 13. The width of a rectangular room is 3/5 of its length x metres. If its perimeter isy metres, write an equation connecting x and y. Find the floor area of the room if its perimeter is 32 m.
Answer :
Length of rectangular room = x m
Width of rectangular room = 3/5 of its length
= 3x/5 m
Perimeter = y m
We know that, Perimeter = 2 (l + b)
y = 2 [(5x + 3x)/5]
By calculation
y = 2 × 8x/5
⇒ y = 16x/5
We get,
5y = 16x
⇒ 16x = 5y …(1)
Equation (1) is the required relation between x and y
Given perimeter = 32 m
So y = 32 m
Now substituting the value of y in equation (1)
16x = 5×32
By calculation
x = (5 × 32)/16
⇒ x = (5 × 2)/1
⇒ x = 10 m
Breadth = 3/5 × x
= 3/5 × 10
= 3×2
= 6 m
Here the floor area of the room = l × b
= 10×6
= 60 m2
Question 14. A rectangular garden 10 m by 16 m is to be surrounded by a concrete walk of uniform width. Given that the area of the walk is 120 square meters, assuming the width of the walk to be x, form an equation in x and solve it to find the value of x.
Answer :
Consider ABCD as a rectangular garden
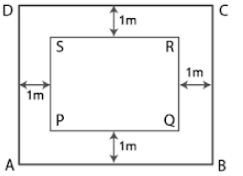
Length = 10 m
Breadth = 16 m
So the area of ABCD = l× b
= 10×16
= 160 m2
Consider x m as the width of the walk
Length of rectangular garden PQRS = 10 – x – x = (10 – 2x) m
Breadth of rectangular garden PQRS = 16 – x – x = (16 – 2x) m
Question 15. A rectangular room is 6 m long, 4.8 m wide and 3.5 m high. Find the inner surface area of the four walls.
Answer :
Length of rectangular room = 6 m
Breadth of rectangular room = 4.8 m
Height of rectangular room = 3.5 m
Here,
Inner surface area of four wall = 2 (l + b) × h
= 2(6 + 4.8)×3.5
By calculation
= 2×10.8×3.5
= 21.6×3.5
= 75.6 m2
(ML Aggarwal Mensuration Exe-16.2 Class 9 ICSE Maths Solutions)
Question 16. A rectangular plot of land measures 41 metres in length and 22.5 metres in width. A boundary wall 2 metres high is built all around the plot at a distance of 1.5 m from the plot. Find the inner surface area of the boundary wall.
Answer :
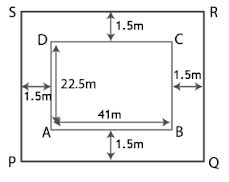
Length of rectangular plot = 41 metres
Breadth of rectangular plot = 22.5 metres
Height of boundary wall = 2 metre
Here,
Boundary wall is built at a distance of 1.5 m
New length = 41 + 1.5 + 1.5
= 41 + 3
= 44 m
New breadth = 22.5 + 1.5 + 1.5
= 22.5 + 3
= 25.5 m
We know that, Inner surface area of the boundary wall = 2 (l + b) × h
= 2×(44 + 25.5)×2
By calculation
= 2 ×69.5× 2
= 2 ×139
= 278 m2
Question 17.
(a) Find the perimeter and area of the figure
(i) given below in which all corners are right angled.
(b) Find the perimeter and area of the figure
(ii) given below in which all corners are right angles.
(c) Find the area and perimeter of the figure
(iii) given below in which all corners are right angles and all measurement in centimetres.

Answer :
(a) It is given that,
AB = 2m, BE = 4m, FE = 4m and FG = 1.5 m
So BD = 4 + 1.5 = 5.5 m
AC = BD = 5.5 m
CG = (4 + 2) = 6 m
We know that, Perimeter of figure (i) = AC + CG + GF + FE + EB + BA
= 5.5 + 6 + 1.5 + 4 + 4 + 2
= 23 m
Here,
Area of given figure = Area of ABEDC + Area of FEDG
It can be written as
= (length × breadth) + (length × breadth)
= (2 × 5.5) + (4 × 1.5)
= 11 + 6
= 17 m2
(b) It is given that
AB = CD = 3m
HI = AC = 7m
JE = BE = 5m
GF = DE = 2m
DG = EF = 8m
GH = JI = 2m
We know that,
CH = CD + DG + GH
= 3 + 8 + 2
= 13 m
Perimeter of the given figure = AB + AC + CH + HI + IJ + JF + FE + BE
= 3 + 7 + 13 + 7 + 2 + 5 + 8 + 5
= 50 m
Here,
Area of given figure = Area of first figure + Area of second figure + Area of third figure
= (7 × 3) + (8 × 2) + (7 × 2)
By calculation
= 21 + 16 + 14
= 51 m2
(c) It is given that
AB = 12 cm
AL = BC = 7 cm
JK = DE = 5 cm
HJ = GF = 3 cm
LK = HG = CD = 2 cm
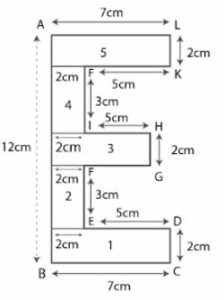
We know that, Perimeter of given figure = AB + BC + CD + DE + EF + FG + GH + HI + IJ + JK + KL + LA
= 12 + 7 + 2 + 5 + 3 + 3 + 2 + 3 + 3 + 5 + 2 + 7
= 54 cm
Here
Area of given figure =Area of first part + Area of second part + Area of third part + Area of fourth part + Area of fifth part
= (7×2) + (2×3) + [(2+3)×2] + (2×3) + (7×2)
By calculation
= 14 + 6 + 10 + 6 + 14
= 50 cm2
Question 18. The length and the breadth of a rectangle are 12 cm and 9 cm respectively. Find the height of a triangle whose base is 9 cm and whose area is one third that of rectangle.
Answer :
Length of a rectangle = 12 cm
Breadth of a rectangle = 9 cm
So the area = l × b
= 12 × 9
= 108 cm2
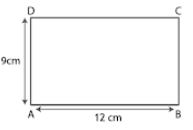
Using the condition
Area of triangle ABC = 1/3 × area of rectangle
= 1/3 × 108
= 36 cm2
Consider h cm as the height of triangle ABC
Area of triangle ABC = ½ × base × height
36 = ½ × 9 × h
By further calculation
36 × 2 = 9 × h
⇒ h = (36 × 2)/9
So we get
h = 4 × 2
⇒ h = 8 cm
Hence, height of triangle ABC is 8 cm.
Question 19. The area of a square plot is 484 mV Find the length of its one side and the length of its one diagonal.
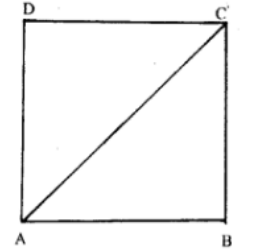
Answer :
ABCD is a square plot having area = 484 m2
Sides of square are AB, BC, CD and AD
We know that, Area of square = side × side
484 = (side)2
So we get
Side = √484 = 22 m
⇒ AB = BC = 22 m
In triangle ABC
Using Pythagoras Theorem
AC2 = AB2 + BC2
AC2 = 222 + 222
⇒ AC2 = 484 + 484 = 968
By further calculation
AC = √968 = √(484×2)
⇒ AC = 22× √2
So we get
AC = 22 × 1.414 = 31.11 m
Hence, length of side is 22 m and length of diagonal is 31.11 m.
(ML Aggarwal Mensuration Exe-16.2 Class 9 ICSE Maths Solutions)
Question 20. A square has the perimeter 56 m. Find its area and the length of one diagonal correct upto two decimal places.
Answer :
Consider ABCD as a square with side x m
Perimeter of square = 4 × side
56 = 4x
By calculation
x = 56/4 = 14 m
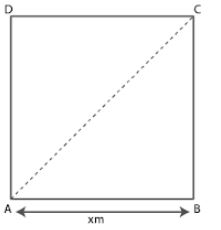
In triangle ABC
Using Pythagoras theorem
AC2 = AB2 + BC2
AC2 = 142 + 142
By calculation
AC2 = 196 + 196 = 392
So we get
AC = √392
⇒ AC = √(196×2)
⇒ AC = 14√2
Substituting the value of √2
AC = 14 × 1.414
⇒ AC = 19.80 m
Hence, the side of square is 14 m and diagonal is 19.80 m.
Mensuration Exercise-16.2
ML Aggarwal Class 9 ICSE Maths Solutions
Page 365
Question 21. A wire when bent in the form of an equilateral triangle encloses an area of 36√3 cm2. Find the area enclosed by the same wire when bent to form:
(i) a square, and
(ii) a rectangle whose length is 2 cm more than its width.
Answer :
Area of equilateral triangle = 36 √3 cm2
Consider x cm as the side of equilateral triangle
Area = √3/4 (side)2
36√3 = √3/4 ×(x)2
By calculation
x2 = (36√3 ×4)/√3
⇒ x2 = 36 × 4
So ,
x = √(36×4)
⇒ x = 6 × 2
⇒ x = 12 cm
Here,
Perimeter of equilateral triangle = 3 × side
= 3 × 12
= 36 cm
(i) We know that, Perimeter of equilateral triangle = Perimeter of square
It can be written as
36 = 4 × side
So we get
Side = 36/4 = 9 cm
Area of square = side × side
= 9 × 9
= 81 cm2
(ii) We know that, Perimeter of triangle = Perimeter of rectangle …(1)
According to the condition of rectangle
Length is 2 cm more than its width
Width of rectangle = x cm
Length of rectangle = (x + 2) cm
Perimeter of rectangle = 2 (l + b)
= 2 [(x+2) + x]
By further calculation
= 2 (2x + 2)
= 4x + 4
Using equation (1)
4x + 4 = Perimeter of triangle
⇒ 4x + 4 = 36
By calculation
4x = 36 – 4 = 32 cm
So we get
x = 32/4 = 8 cm
Here,
Length of rectangle = 8 + 2 = 10 cm
Breadth of rectangle = 8 cm
Area of rectangle = length × breadth
= 10×8
= 80 cm2
Question 22. Two adjacent sides of a parallelogram are: 15 cm and 10 cm. If the distance between the longer sides is 8 cm, find the area of the parallelogram. Also find the distance between shorter sides.
Answer :
ABCD as a parallelogram
Longer side AB = 15 cm
Shorter side = 10 cm
Distance between longer side DM = 8 cm
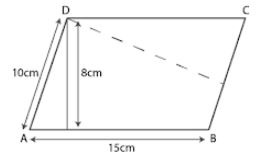
Consider DN as the distance between the shorter side
Area of parallelogram ABCD = base × height
We can write it as
= AB×DM
= 15 × 8
= 120 cm2
If base is AD
Area of parallelogram = AD × DN
120 = 10 × DN
So ,
DN = 120/10 = 12 cm
Hence, the area of parallelogram is 120 cm2 and the distance between shorter side is 12 cm.
(ML Aggarwal Mensuration Exe-16.2 Class 9 ICSE Maths Solutions)
Question 23. ABCD is a parallelogram with sides AB = 12 cm, BC = 10 cm and diagonal AC = 16 cm. Find the area of the parallelogram. Also find the distance between its shorter sides.
Answer :
It is given that
ABCD is a parallelogram
AB = 12 cm, BC = 10 cm and AC = 16 cm
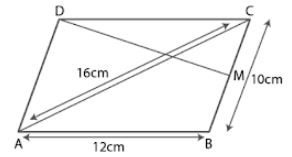
Area of triangle ABC
BC = a = 10 cm
AC = b = 16 cm
AB = c = 12 cm
We know that
s = (a + b + c)/2
s = (10 + 16 + 12)/2
By further calculation
s = 38/2 = 19 cm
Here,
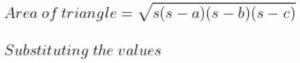
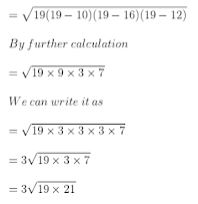
3√399 cm2
Area of parallelogram = 2 × Area of triangle ABC
= 2 × 3√399
= 6 √399
So we get
= 6 × 19.96
= 119.8 cm2
Consider DM as the distance between the shorter lines
Base = AD = BC = 10 cm
Area of parallelogram = AD × DM
119.8 = 10 × DM
By calculation
DM = 119.8/10
⇒ DM = 11.98 cm
Hence, the distance between shorter lines is 11.98 cm.
Question 24. Diagonals AC and BD of a parallelogram ABCD intersect at O. Given that AB = 12 cm and perpendicular distance between AB and DC is 6 cm. Calculate the area of the triangle AOD.
Answer :
It is given that
ABCD is a parallelogram
AC and BD are the diagonal which intersect at O
AB = 12 cm and DM = 6 cm
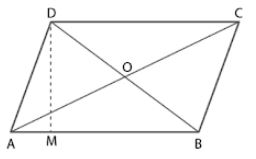
We know that
Area of parallelogram ABCD = AB×DM
= 12 × 6
= 72 cm2
Area of triangle AOD = ¼ × Area of parallelogram
= ¼ × 72
= 18 cm2
Question 25. ABCD is a parallelogram with side AB = 10 cm. Its diagonals AC and BD are of length 12 cm and 16 cm respectively. Find the area of the parallelogram ABCD.
Answer :
ABCD is a parallelogram
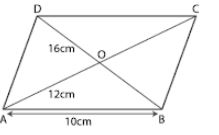
AB = 10 cm, AC = 12 cm
AO = CO = 12/2 = 6 cm
BD = 16 cm
BO = OD = 16/2 = 8 cm
In triangle AOB
a = 10 cm, b = AO = 6 cm, c = BO = 8 cm
s = (a + b + c)/2
s = (10 + 6 + 8)/2
By calculation
s = 24/2 = 12 cm
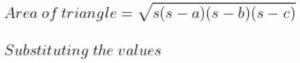
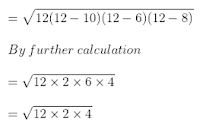
= 12×2
= 24 cm2
We know that, Area of parallelogram ABCD = 4 × Area of triangle AOB
= 4×24
= 96 cm2
Question 26. The area of a parallelogram is p cm2 and its height is q cm. A second parallelogram has equal area but its base is ‘r’ cm more than that of the first. Obtain an expression in terms of p, q and r for the height h of the second parallelogram.
Answer :
Area of a parallelogram = p cm2
Height of first parallelogram = q cm
We know that, Area of parallelogram = base × height
p = base × q
Base = p/q
Here
Base of second parallelogram = (p/q + r)
Taking LCM
= (p + qr)/ q cm
Area of second parallelogram = Area of first parallelogram = p cm2
It can be written,
Base × height = p cm2
[(p + qr)/q] × h = p
So we get
h = pq/(p + qr) cm
Hence, the height of second parallelogram is h = pq/(p + qr) cm.
(ML Aggarwal Mensuration Exe-16.2 Class 9 ICSE Maths Solutions)
Question 27. What is the area of a rhombus whose diagonals are 12 cm and 16 cm ?
Answer :
It is given that
ABCD is a rhombus
BD = 12 cm and AC = 16 cm are diagonals
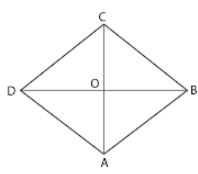
We know that
Area of rhombus ABCD = ½ × AC × BD
Substituting the values
= ½ × 16 × 12
By further calculation
= 8 × 12
= 96 cm2
Question 28. The area of a rhombus is 98 cm². If one of its diagonal is 14 cm, what is the length of the other diagonal?
Answer :
It is given that
Area of rhombus = 98 cm2
One of its diagonal = 14 cm
We know that, Area of rhombus = ½ ×product of diagonals
98 = ½ ×one diagonal ×other diagonal
⇒ 98 = ½ ×14 ×other diagonal
By calculation
Other diagonal = (98×2)/14
= 7 × 2
= 14 cm
Hence, the other diagonal is 14 cm.
Question 29. The perimeter of a rhombus is 45 cm. If its height is 8 cm, calculate its area.
Answer :
It is given that
ABCD is a rhombus
Consider x cm as each side

Perimeter = 45 cm
AB + BC + CD + AD = 45 cm
x + x + x + x = 45
⇒ 4x = 45
By division
x = 45/4 cm
Height = 8 cm
Area of rhombus = base × height
= 45/4 ×8
= 45 ×2
= 90 cm2
(ML Aggarwal Mensuration Exe-16.2 Class 9 ICSE Maths Solutions)
Question 30. PQRS is a rhombus. If it is given that PQ = 3 cm and the height of the rhombus is 2.5 cm, calculate its area.
Answer :
PQRS is a rhombus
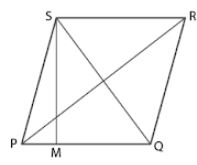
PQ = 3 cm
Height = 2.5 cm
Consider PQ as the base of rhombus PQRS.
SM = 2.5 cm is the height of rhombus
We know that, Area of rhombus PQRS = base × height
= 3 ×2.5
= 7.5 cm2
Question 31. If the diagonals of a rhombus are 8 cm and 6 cm, find its perimeter.
Answer :
ABCD as a rhombus with AC and BD as two diagonals
Here
AC = 8 cm and BD = 6 cm
AO = 4 cm and BO = 3 cm
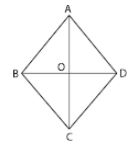
In triangle ABC
Using Pythagoras theorem
AB2 = AO2 + BO 2
AB2 = 42 + 32
By calculation
AB2 = 16 + 9 = 25
So we get
AB = √25 = 5 cm
Side of rhombus ABCD = 5 cm
Here
Perimeter of rhombus = 4 × side
= 4 × 5
= 20 cm
Question 32. If the sides of a rhombus are 5 cm each and one diagonal is 8 cm, calculate
(i) the length of the other diagonal, and
(ii) the area of the rhombus.
Answer :
(i) It is given that
ABCD is a rhombus with side AB, BC, CD and AD
AB = BC = CD = AD = 5 cm
AC = 8 cm and AO = 4 cm

In triangle AOB
Using Pythagoras theorem
AB2 = AO2 + BO2
52 = 42 + BO2
By calculation
25 = 16 + BO2
⇒ BO2 = 25 – 16 = 9
So ,
BO = √9 = 3 cm
⇒ BD = 2 × BO = 2 × 3 = 6 cm
Length of other diagonal = 6 cm
(ii) Area of rhombus = ½ × product of diagonals
= ½ × 8 × 6
By calculation
= 4 × 6
= 24 cm2
(ML Aggarwal Mensuration Exe-16.2 Class 9 ICSE Maths Solutions)
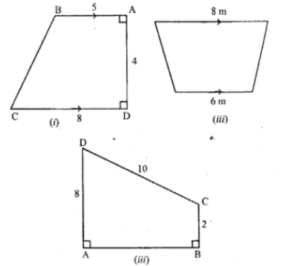
Question 33.
(a) The diagram (t) given below is a trapezium. Find the length of BC and the area of the trapezium Assume AB = 5 cm, AD = 4 cm, CD = 8 cm
(b) The diagram (ii) given below is a trapezium Find (i) AB (ii) area of trapezium ABCD.
(c) The cross-section of a canal is shown in figure (iii) given below. If the canal is 8 m wide at the top and 6 m wide at the bottom and the area of the cross-section is 16.8 m², calculate its depth
Answer :
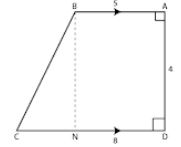
(a) It is given that
ABCD is a trapezium
AB = 5 cm, AD = 4 cm and CD = 8 cm
Construct BN perpendicular to CD
Here,
BN = 4 cm
CN = CD – ND
⇒ CN = CD – AO
⇒ CN = 8 – 5 = 3 cm
In triangle BCN
Using Pythagoras theorem
BC2 = BN2 + CN2
BC2 = 42 + 32
By calculation
BC2 = 16 + 9 = 25
⇒ BC = √25 = 5 cm
Length of BC = 5 cm
Area of trapezium = ½ ×sum of parallel sides ×height
It can be written as
= ½ × (AB + CD) × AD
= ½ × (5 + 8) × 4
By calculation
= ½ × 13 × 4
So we get
= 13 × 2
= 26 cm2
Area of trapezium = 26 cm2
(b) From the figure (ii)
AD = 8 units
BC = 2 units
CD = 10 units
Construct CN perpendicular to AD
AN = 2 units
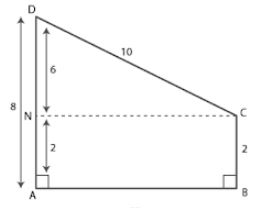
We know that
DN = AD – DN
Substituting the values
= 8 – 6
= 2 units
In triangle CDN
Using Pythagoras theorem
CD2 = DN2 + NC2
Substituting the values
102 = 62 + NC2
By further calculation
NC2 = 102 – 62
⇒ NC2 = 100 – 36 = 64
So we get
NC = √64 = 8 units
From the figure NC = AB = 8 units
We know that
Area of trapezium = ½ × sum of parallel sides × height
It can be written as
= ½ ×(BC + AD)×AB
Substituting the values
= ½ ×(2 + 8)×8
By further calculation
= ½ ×10×8
= 5 × 8
= 40 sq. units
(c) Consider ABCD as the cross section of canal in the shape of trapezium.
AB = 6 m, DC = 8 m
Take AL as the depth of canal
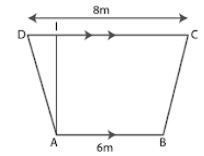
So the area of cross-section = 16.8 m2
It can be written as
½ × sum of parallel sides × depth = 16.8
⇒ ½ × (AB + DC) × AL = 16.8
Substituting the values
½ × (6 + 8) × AL = 16.8
By further calculation
½ × 14 × AL = 16.8
⇒ AL = (16.8 × 2)/14
So we get
AL = (16.8×1)/7
⇒ AL = 2.4 m
Mensuration Exercise-16.2
ML Aggarwal Class 9 ICSE Maths Solutions
Page 366
Question 34. The distance between parallel sides of a trapezium is 12 cm and the distance between mid-points of other sides is 18 cm. Find the area of the trapezium.
Answer :
Consider ABCD as a trapezium in which AB || DC
Height CL = 12 cm
E and F are the mid-points of sides AD and BC
EF = 18 cm
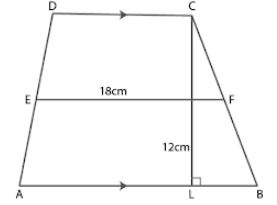
We know that
EF = ½ (AB + DC) = 18 cm
Here
Area of trapezium ABCD = ½ (AB + DC) ×height
Substituting the values
= 18 × 12
= 216 cm2
Question 35. The area of a trapezium is 540 cm². If the ratio of parallel sides is 7 : 5 and the distance between them is 18 cm, find the length of parallel sides.
Answer :
Area of trapezium = 540 cm2
Ratio of parallel sides = 7: 5
Consider 7x cm as one parallel side
Other parallel side = 5x cm
Distance between the parallel sides = height = 18 cm
We know that, Area of trapezium = ½ × sum of parallel sides × height
Substituting the values
540 = ½ × (7x + 5x) × 18
By calculation
540 = ½ × 12x × 18
⇒ 540 = 6x × 18
⇒ 540 = 108x
⇒ x = 540/108 = 5
Here
First parallel side = 7x = 7 × 5 = 35 cm
Second parallel side = 5x = 5 × 5 = 25 cm
(ML Aggarwal Mensuration Exe-16.2 Class 9 ICSE Maths Solutions)
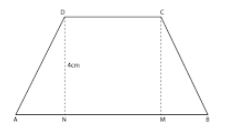
Question 36. The parallel sides of an isosceles trapezium are in the ratio 2 : 3. If its height is 4 cm and area is 60 cm2, find the perimeter.
Answer :
ABCD is an isosceles trapezium
BC = AD
Height = 4 cm
Consider CD = 2x and AB = 3x
Area of trapezium = ½ (sum of parallel sides)×height
Substituting the values
60 = ½ × (2x + 3x) × 4
By further calculation
60 = ½ × 5x × 4
⇒ 60 = 5x × 2
⇒ 60 = 10x
So we get
x = 60/10 = 6
Here,
CD = 2x = 2 × 6 = 12 cm
AB = 3x = 3 × 6 = 18 cm
AN = BM
We can write it as
AN = AB – BN
⇒ AN = AB – (MN + BM)
MN = CD
⇒ AN = AB – (CD + BM)
Similarly BM = AN
AN = AB – (CD + AN)
Substituting the values
AN = 18 – (12 + AN)
⇒ AN = 18 – 12 – AN
⇒ AN + AN = 6
⇒ 2AN = 6
By division
AN = 6/2 = 3
In triangle AND
Using Pythagoras theorem
AD2 = DN2 + AN2
Here DN = 4 cm
AD2 = 42 + 32
By further calculation
AD2 = 16 + 9 = 25
So we get
AD= √25 = 5 cm
Here AD = BC = 5 cm
Perimeter of trapezium = AB + BC + CD + AD
= 18 + 5 + 12 + 5
= 40 cm
Question 37. The area of a parallelogram is 98 cm². If one altitude is half the corresponding base, determine the base and the altitude of the parallelogram.
Answer :
Area of parallelogram = 98 cm2
Condition – If one altitude is half the corresponding base
Take base = x cm
Corresponding altitude = x/2 cm
Area of parallelogram = base × altitude
98 = x × x/2
⇒ 98 = x2/2
By cross multiplication
x2 = 98 × 2 = 196
So we get
x = √196 = 14 cm
Base = 14 cm
Here,
altitude = 14/2 = 7 cm
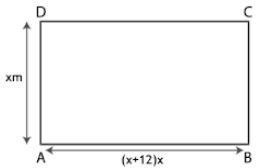
Question 38. The length of a rectangular garden is 12m more than its breadth. The numerical value of its area is equal to 4 times the numerical value of its perimeter. Find the dimensions of the garden
Answer :
The dimensions of rectangular garden are
Breadth = x m
Length = (x + 12) m
We know that
Area = l × b
Area = (x + 12) × x
⇒ Area = (x2 + 12x) m2
Perimeter = 2 (l + b)
= 2 [(x + 12) + x]
= 2 [ x + 12 + x]
= 2 [2x + 12]
= (4x + 24) m
Numerical value of area = 4 × numerical value of perimeter
x 2 + 12x = 4 × (4x + 24)
By calculation
x2 + 12x = 16x + 96
⇒ x2 + 12x – 16x – 96 = 0
⇒ x2 – 4x – 96 = 0
It can be written as
x2 – 12x + 8x – 96 = 0
Taking out the common terms
x (x – 12) + 8 (x – 12) = 0
⇒ (x + 8) (x – 12) = 0
Here,
x + 8 = 0 or x – 12 = 0
So ,
x = -8 (not possible) or x = 12
Breadth of rectangular garden = 12 m
Length of rectangular garden = 12 + 12 = 24 m
Question 39. If the perimeter of a rectangular plot is 68 m and length of its diagonal is 26 m, find its area.
Answer :
It is given that
Perimeter of a rectangular plot = 68 m
Length of its diagonal = 26 m
ABCD is a rectangular plot of length x m and breath y m
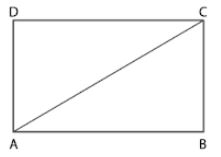
Perimeter = 2 (length + breadth)
68 = 2 (x + y)
By calculation
68/2 = x + y
⇒ 34 = x + y
So we get
x = 34 – y …(1)
In triangle ABC
Using Pythagoras theorem
AC2 = AB2 + BC2
262 = x2 + y2
⇒ x2 + y2 = 676
Now substituting the value of x in equation (1)
(34 – y)2 + y2 = 676
⇒ 1156 + y2 – 68y + y2 = 676
By calculation
2y2 – 68y + 1156 – 676 = 0
⇒ 2y2 – 68y – 480 = 0
Taking 2 as common
2 (y2 – 34y – 240) = 0
⇒ y2 – 34y – 240 = 0
It can be written as
y2 – 24y – 10y – 240 = 0
Taking out the common terms
y (y – 24) – 10 (y – 24) = 0
⇒ (y – 10) (y – 24) = 0
Here,
y – 10 = 0 or y – 24 = 0
y = 10 m or y = 24 m
Now substituting the value of y in equation (1)
y = 10 m, x = 34 – 10 = 24 m
y = 24 m, x = 34 – 24 = 10 m
Area in both cases = xy
= 24×10 or 10×24
= 240 m2
Hence, the area of the rectangular block is 240 m2.
Question 40. A rectangle has twice the area of a square. The length of the rectangle is 12 cm greater and the width is 8 cm greater than 2 side of a square. Find the perimeter of the square.
Answer :
Side of a square = x cm
Length of rectangle = (x + 12) cm
Breadth of rectangle = (x + 8) cm
We know that, Area of square = side × side = x×x = x2 cm2
Area of rectangle = l × b
= (x + 12) (x + 8) cm2
Based on the question
Area of rectangle = 2 ×area of square
(x + 12) (x + 8) = 2 × x2
It can be written as
x (x + 8) + 12 (x + 8) = 2x2
⇒ x2 + 8x + 12x + 96 = 2x2
⇒ x2 – 2x2 + 8x + 12x + 96 = 0
By calculation
-x2 + 20x + 96 = 0
⇒ -(x2 – 20x – 96) = 0
⇒ x2 – 20x – 96 = 0
We can write,
x2 – 24x + 4x – 96 = 0
⇒ x (x – 24) + 4 (x – 24) = 0
⇒ (x + 4) (x – 24) = 0
Here,
x + 4 = 0 or x – 24 = 0
⇒ x = -4 or x = 24 cm
Side of square = 24 cm
Perimeter of square = 4 × side
= 4 × 24
= 96 cm
(ML Aggarwal Mensuration Exe-16.2 Class 9 ICSE Maths Solutions)
Question 41. The perimeter of a square is 48 cm. The area of a rectangle is 4 cm2 less than the area of the square. If the length of the rectangle is 4 cm greater than its breadth, find the perimeter of the rectangle.
Answer :
Perimeter of a square = 48 cm
Side = perimeter/4 = 48/4 = 12 cm
We know that, Area = side2 = 122 = 144 cm2
Area of rectangle = 144 – 4 = 140 cm2
Take breadth of rectangle = x cm
Length of rectangle = x + 4 cm
So the area = (x + 4) × x cm2
(x + 4) x = 140
By further calculation
x2 + 4x – 140 = 0
⇒ x2 + 14x – 10x – 140 = 0
Taking out the common terms
x (x + 14) – 10 (x + 14) = 0
⇒ (x + 14) (x – 10) = 0
Here,
x + 14 = 0 where x = – 14
x – 10 = 0 where x = 10
Breadth = 10 cm
Length = 10 + 4 = 14 cm
Perimeter = 2 (l + b)
= 2 (14 + 10)
= 2 × 24
= 48 cm
Question 42. In the adjoining figure, ABCD is a rectangle with sides AB = 10 cm and BC = 8 cm. HAD and BFC are equilateral triangles; AEB and DCG are right angled isosceles triangles. Find the area of the shaded region and the perimeter of the figure.
Answer :

It is given that
ABCD is a rectangle with sides AB = 10 cm and BC = 8 cm
HAD and BFC are equilateral triangle with each side = 8 cm
AEB and DCG are right angled isosceles triangles with hypotenuse = 10 cm
Consider AE = EB = x cm
In triangle ABE
AE2 + EB2 = AB2
Substituting the values
x2 + x2 = 102
⇒ 2x2 = 100
By further calculation
x2 = 100/2 = 50
⇒ x = √50 = √(25 × 2) = 5√2 cm
We know that
Area of triangle AEB = Area of triangle GCD
It can be written as
= ½ × x × x
= ½ x2 cm2
Substituting the value of x
= ½ × 50
= 25 cm2
Area of triangle HAD = Area of BFC
It can be written as
= √3/4 × 82
= √3/4 × 64
= 16√3 cm2
Area of shaded portion = Area of rectangle ABCD + 2 area of triangle AEB + 2 area of triangle BFC
Substituting the values
= (10×8) + (2×25) + (2×16√3)
By further calculation
= 80 + 50 + 32√3
So we get
= (130 + 32√3) cm2
Here
Perimeter of the figure = AE + EB + BF + FC + CD + GD + DH + HA
It can be written as
= 4AE + 4BF
Substituting the values
= (4×5√2) + (4×8)
So we get
= 20√2 + 32
= (32 + 20√2) cm
(ML Aggarwal Mensuration Exe-16.2 Class 9 ICSE Maths Solutions)
Question 43.
(a) Find the area enclosed by the figure (i) given below, where ABC is an equilateral triangle and DGFG is an isosceles trapezium.
All measurements are in centmetres.
(b) Find the area enclosed by the figure (ii) given below. AH measurements are in centimetres.
(c) In the figure (iii) given below, from a 24. cm x 24 cm piece of cardboard, a block in the shape of letter M is cut off. Find the area of the cardboard left over, all measurements are in centimetres.

Answer :
(a) It is given that
ABC is an equilateral triangle and DEFG is an isosceles trapezium
EF = GD = 5 cm
DE = 6 cm
GF = GB + BC + CF
= 3 + 6 + 3
= 12 cm
AB = AC = BC = 6 cm
Join BD and CE
In right triangle CEF
CE2 = EF2 – CF2
= 52 – 32
= 25 – 9
= 16
So,
CE = √16 = 4 cm
Area of triangle ABC = √3/4 × 62
By calculation
= √3/4 × 36
= 9√3 cm2
Area of trapezium DEFG = ½ (DE + GF) × CE
= ½ ×(6+12)× 4
By further calculation
= ½ ×18×4
= 36 cm2
So the area of figure = 9√3 + 36
= 9 × 1.732 + 36
= 15.59 + 36
= 51.59 cm2
(b) We know that, Length of rectangle = 2 + 2 + 2 + 2 = 8 cm
Width of rectangle = 2 cm
Area of rectangle = l × b
= 8 × 2
= 16 cm2
Here
Area of each trap = ½ (2+2) × (6–2)
By calculation
= ½ × 4 × 4
= 8 cm2
So the total area = area of rectangle + area of 2 trapezium
= 16 + 8 + 8
= 32 cm2
(c) We know that, Length of each rectangle = 24 cm
Width of each rectangle = 6 cm
Area of each rectangle = l × b
Substituting the values
= 24 × 6
= 144 cm2
Base of each parallelogram = 8 cm
Height of each parallelogram = 6 cm
So the area of each parallelogram = 8 × 6 = 48 cm2
Here,
Area of the M-shaped figure = (2×144) + (2×48)
So we get
= 288 + 96
= 384 cm2
Area of the square cardboard = 24 × 24 = 576 cm2
Area of the removing cardboard = 576 – 384 = 192 cm2
Mensuration Exercise-16.2
ML Aggarwal Class 9 ICSE Maths Solutions
Page 367
Question 44.
(a) The figure (i) given below shows the cross-section of the concrete structure with the measurements as given. Calculate the area of cross-section.
(b) The figure (ii) given below shows a field with the measurements given in metres. Find the area of the field.
(c) Calculate the area of the pentagon ABCDE shown in fig. (iii) below, given that AX = BX = 6 cm, EY = CY = 4 cm, DE = DC = 5cm,DX = 9cmand DX is perpendicular to EC and AB.

Answer :
(a) From the figure (i)
AB = 1.8 m, CD = 0.6 m, DE = 1.2 m
EF = 0.3 m, AF = 2.4 m
Construct DE to meet AB in G
∠FEG = ∠GAF = 900
So, AGEF is a rectangle
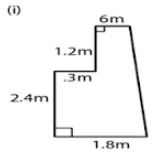
We know that, Area of given figure = Area of rectangle AGEF + Area of trapezium GBCD
It can be written as
= (l × b) + ½ (sum of parallel sides× height)
= (AF×AG) + ½ (GB+CD)×DG
= (2.4×0.3) + ½ [(AB – AG) + CD]×(DE + EG)
Here AG = FE and using EG = AF
= 0.72 + ½ [(1.8–0.3) + 0.6]×(1.2 + 2.4)
By calculation
= 0.72 + ½ [1.5+0.6]×3.6
= (0.72 + ½) × (2.1× 3.6)
So,
= 0.72 + (2.1×1.8)
= 0.72 + 3.78
= 4.5 m2
(b) ABCD is a pentagonal field
AX = 12 m, BX = 30 m, XZ = 15 m, CZ = 25 m,
DZ = 10 m, AD = 12 + 15 + 10 = 37 m, EY = 20 m

We know that, Area of pentagonal field ABCDE = Area of triangle ABX + Area of trapezium BCZX + Area of triangle CDZ + Area of triangle AED
It can be written as
= (½ ×base × height) + [½ (sum of parallel sides)×height] + [½ × base × height] + [½ × base × height]
= [½ ×BX×AX] + [½ (BX + CZ)×XZ] + [½ ×CZ×DZ] + [½ ×AD×EY]
= [½×30×12] + [½ (30+25)×15] + [½×25×10] + [½ ×37×20]
By calculation
= [15×12] + [7.5×55 ]+ [25×5] + [37×10]
So ,
= 180 + 412.5 + 125 + 370
= 1087.5 m2
(c) It is given that ABCDE is a pentagon
AX = BX = 6 cm, EY = CY = 4 cm
DE = DC = 5 cm, DX = 9 cm
Construct DX perpendicular to EC and AB

In triangle DEY
Using Pythagoras Theorem
DE2 = DY2 + EY2
52 = DY2 + 42
⇒ 25 = DY2 + 16
⇒ DY2 = 25 – 16 = 9
So ,
DY = √9 = 3 cm
Here,
Area of pentagonal field ABCDE = Area of triangle DEY + Area of triangle DCY + Area of trapezium EYXA + Area of trapezium CYXB
It can be written as
= (½ ×base× height) + (½ ×base ×height) + [½ ×(sum of parallel sides) ×height] + [½ ×(sum of parallel sides) ×height]
= [½ ×EY ×DY] + [½ ×CY ×DY] + [½ ×(EY + AX) ×XY] + [½ ×(CY + BX) ×XY]
= [½ ×4 ×3] + [½ ×4 ×3] + [½ ×(4+6) ×(DX – DY)] + [½ (4+6) ×(DX – DY)]
By calculation
= (2×3) + (2×2) + [½× 10×(9 – 3)] + [½ ×10 ×(9 – 3)]
So we get
= 6 + 6 + (5×6) + (5×6)
= 6 + 6 + 30 + 30
= 72 cm2
(ML Aggarwal Mensuration Exe-16.2 Class 9 ICSE Maths Solutions)
Question 45. If the length and the breadth of a room are increased by 1 metre the area is increased by 21 square metres. If the length is increased by 1 metre and breadth is decreased by 1 metre the, area is decreased by 5 square metres. Find the perimeter of the room.
Answer :
Take length of room = x m
Breadth of room = y m
Here,
Area of room = l × b = xy m2
We know that, Length is increased by 1 m then new length = (x + 1) m
Breadth is increased by 1 m then new breadth = (y + 1) m
So the new area = new length × new breadth
= (x + 1) (y + 1) m2
Based on the question
xy = (x + 1) (y + 1) – 21
By further calculation
xy = x (y + 1) + 1 (y + 1) – 21
⇒ xy = xy + x + y + 1 – 21
So we get
0 = x + y + 1 – 21
⇒ 0 = x + y – 20
⇒ x + y – 20 = 0
⇒ x + y = 20 …(1)
Length is increased by 1 metre then new length = (x + 1) metre
Breadth is decreased by 1 metre than new breadth = (y – 1) metre
So the new area = new length × new breadth
= (x + 1) (y – 1) m2
Based on the question
xy = (x + 1) (y – 1) + 5
By calculation
xy = x (y – 1) + 1 (y – 1) + 5
⇒ xy = xy – x + y – 1 + 5
⇒ 0 = -x + y + 4
So we get
x – y = 4 …(2)
By adding equations (1) and (2)
2x = 24
⇒ x = 24/2 = 12 m
Now substituting the value of x in equation (1)
12 + y = 20
⇒ y = 20 – 12 = 8 m
Here
Length of room = 12 m
Breadth of room = 8 m
So the perimeter = 2 (l + b)
= 2 (12 + 8)
= 2 × 20
= 40 m
Question 46. A triangle and a parallelogram have the same base and same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Answer :
Sides of a triangle = 26 cm, 28 cm and 30 cm
We know that, s = (a + b + c)/2
Substituting the values
s = (26 + 28 + 30)/ 2
⇒ s = 84/2
⇒ s = 42 cm
Here,
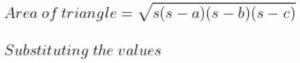
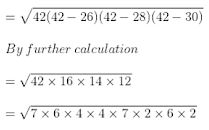
So we get
= 2 × 4 × 6 × 7
= 336 cm2
We know that, Base = 28 cm
Height = Area/base
= 336/28
= 12 cm
Question 47. A rectangle of area 105 cm² has its length equal to x cm. Write down its breadth in terms of x. Given that its perimeter is 44 cm, write down an equation in x and solve it to determine the dimensions of the rectangle.
Answer :
Area of rectangle = 105 cm2
Length of rectangle = x cm
We know that, Area = length × breadth
105 = x × breadth
⇒ x = 105/x cm
Perimeter of rectangle = 44 cm
So,
2 (l + b) = 44
⇒ 2 (x + 105/x) = 44
By calculation
(x2 + 105)/ x = 22
By cross multiplication
x2 + 105 = 22x
⇒ x2 – 22x + 105 = 0
x2 – 15x – 7x + 105 = 0
⇒ x(x – 15) – 7(x – 15) = 0
⇒ (x – 7) (x – 15) = 0
Here,
x – 7 = 0 or x – 15 = 0
⇒ x = 7 cm or x = 15 cm
If x = 7 cm,
Breadth = 105/7 = 15 cm
If x = 15 cm,
Breadth = 105/15 = 7 cm
Hence, the required dimensions of rectangle are 15 cm and 7 cm.
(ML Aggarwal Mensuration Exe-16.2 Class 9 ICSE Maths Solutions)
Question 48. The perimeter of a rectangular plot is 180 m and its area is 1800 m². Take the length of plot as x m. Use the perimeter 180 m to write the value of the breadth in terms of x. Use the value of the length, breadth and the area to, write an equation in x. Solve the equation to calculate the length and breadth of the plot.
Answer :
Perimeter of a rectangular plot = 180 m
Area of a rectangular plot = 1800 m2
Take length of rectangle = x m
Here
Perimeter = 2 (length + breadth)
180 = 2 (x + breadth)
⇒ 180/2 = x + breadth
⇒ x + breadth = 90
⇒ Breadth = 90 – x m
Area of rectangle = l × b
1800 = x × (90 – x)
⇒ 90x – x2 = 1800
It can be written as
– (x2 – 90x) = 1800
⇒ x2 – 90x = – 1800
By calculation
x2 – 90x + 1800 = 0
⇒ x2 – 60x – 30x + 1800 = 0
⇒ x (x – 60) – 30 (x – 60) = 0
⇒ (x – 30) (x – 60) = 0
Here,
x – 30 = 0 or x – 60 = 0
⇒ x = 30 or x = 60
If x = 30 m
Breadth = 90 – 30 = 60 m
If x = 60 m
Breadth = 90 – 60 = 30 m
Hence, the required length of rectangle is 60 m and the breadth of rectangle is 30 m.
— : End of ML Aggarwal Mensuration Exe-16.2 Class 9 ICSE Maths Solutions :–
Return to :- ML Aggarawal Maths Solutions for ICSE Class-9
Thanks
Please Share with Your Friends