ML Aggarwal Mensuration Exe-17.4 Class 10 ICSE Maths Solutions. We Provide Step by Step Answer of Exe-17.4 Questions for Mensuration as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Mensuration Exe-17.4 Class 10 ICSE Maths Solutions
| Board | ICSE |
| Subject | Maths |
| Class | 10th |
| Chapter-17 | Mensuration |
| Writer / Book | Understanding |
| Topics | Solutions of Exe-17.4 |
| Academic Session | 2024-2025 |
Mensuration Exe-17.4
ML Aggarwal Class 10 ICSE Maths Solutions
Page 423
Take π = 22/7, unless stated otherwise.
Question 1. The adjoining figure shows a cuboidal block of wood through which a circular cylindrical hole of the biggest size is drilled. Find the volume of the wood left in the block.
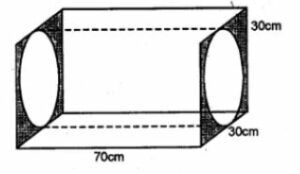
Answer :
Diameter of the biggest hole = 30 cm.
Radius (r) = 30/2 = 15 cm
and height (h) = 70 cm.
Volume of the cuboidal block = lbh
= 70 × 30 × 30
= 63000 cm3
Volume of cylindrical hole = r2h
= (22/7) × 152 × 70
= 22 × 225 × 10
= 49500 cm3
Volume of the wood left in the block = 63000 – 49500 = 13500 cm3
Hence,
the volume of the wood left in the block is 13500 cm3.
Question 2. The given figure shows a solid trophy made of shining glass. If one cubic centimetre of glass costs Rs 0.75, find the cost of the glass for making the trophy.

Answer :
Edge of cubical part = 28 cm
and radius of cylindrical part (r) = 28/2 = 14cm
Height of the cylinder, h = 28 cm
Volume of the cube = a3
= 283
= 28×28×28
= 21952 cm3
Volume of the cylinder = r2h
= (22/7)×142×28
= 22×2×14×28
= 17248 cm3
Total volume of the solid = Volume of the cube + volume of the cylinder
= 21952+17248
= 39200 cm3
Cost of 1 cm3 glass = Rs. 0.75
Total cost of glass = 39200×0.75
= Rs. 29400
Hence the cost of making the trophy is Rs. 29400.
Question 3. From a cube of edge 14 cm, a cone of maximum size is carved out. Find the volume of the remaining material.
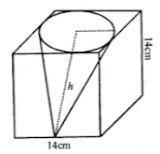
Answer :
Edge of a cube = 14 cm
Volume = (side)³ = (14)³ = 14 × 14 × 14 cm³ = 2744 cm³
Now diameter of the cone cut out from it = 14 cm
Volume of the cube = a3
= 143
= 14 × 14 × 14
= 2744 cm3
Volume of the cone = (1/3)πr2h
= (1/3) × (22/7) × 72 × 14
= 22 × 7 × 14/3
= 2156/3 cm3
Volume of the remaining material = Volume of the cube – Volume of the cone
= (2744 – 2156)/3
= (3 × 2744 – 2156)/3
= (8232 – 2156)/3
= 6076/3
= 2025.1/3 cm3
Hence the volume of the remaining material is 2025.1/3 cm3
(ML Aggarwal Mensuration Exe-17.4 Class 10)
Question 4. A cone of maximum volume is curved out of a block of wood of size 20 cm x 10 cm x 10 cm. Find the volume of the remaining wood.
Answer :
Given dimensions of the block of wood = 20 cm × 10 cm × 10 cm
Volume of the block of wood = 20 × 10× 10 = 2000 cm3 [Volume = lbh]
Diameter of the cone, d = 10 cm
Radius of the cone, r = d/2 = 10/2 = 5 cm
Height of the cone, h = 20 cm
Volume of the cone = (1/3)πr2h
= (1/3) × (22/7) × 52 × 20
= (22 × 25 × 20)/(3 × 7)
= 11000/21 cm3
Volume of the remaining wood = Volume of block of wood – Volume of cone
= (2000 – 11000)/21
= (21×2000 – 11000)/21
= (42000 – 11000)/21
= 31000/21
= 1476.19 cm3
Hence,
the volume of the remaining wood is 1476.19 cm3.
Question 5. 16 glass spheres each of radius 2 cm are packed in a cuboidal box of internal dimensions 16 cm x 8 cm x 8 cm and then the box is filled with water. Find the volume of the water filled in the box.
Answer :
Given :
dimensions of the box = 16 cm × 8 cm × 8 cm
So volume of the box = lbh = 16 × 8 × 8 = 1024 cm3
Radius of the glass sphere, r = 2 cm
Volume of the sphere = (4/3)πr3
= (4/3) × (22/7) × 23
= (4 × 22 × 8)/(3 × 7)
= 704/21
Volume of 16 spheres = (16 × 704)/21 = 11264/21 = 536.38 cm3
Volume of water filled in the box = Volume of the box – Volume of 16 spheres
= 1024 – 536.38
= 487.62 cm3
Hence,
the volume of the water filled in the box is 487.62 cm3.
(ML Aggarwal Mensuration Exe-17.4 Class 10)
Question 6. A cuboidal block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter that the hemisphere can have? Also, find the surface area of the solid.
Answer :
Side of cuboidal = 7 cm
Diameter of hemisphere = 7 cm
and radius (r) = 7/2 cm
= 3.5 cm
Surface area of the hemisphere = 2πr2
= 2 × (22/7) × 3.52
= 44 × 12.25/7
= 539/7
= 77 cm2
Surface area of the cube = 6a2
= 6 × 72
= 6 × 49
= 294 cm2
Surface area of base of hemisphere = πr2
= (22/7) × 3.52
= 22 × 12.25/7
= 38.5 cm2
Surface area of the solid = surface area of the cube + surface area of hemisphere – surface area of the base of hemisphere
= 294 + 77 – 38.5
= 332.5 cm2
Hence,
the surface area of the solid is 332.5 cm2.
Question 7. A wooden article was made by scooping out a hemisphere from each end of a solid cylinder (as shown in the given figure). If the height of the cylinder is 10 cm and its base is of radius 3.5 cm, find the total surface area of the article.
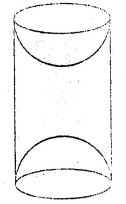
Answer :
Height of the cylinder = 10 cm
and radius of the base = 3.5 cm
Total surface area
= Curved surface area of cylinder + 2 × Curved surface area of hemisphere
= 2πrh + 2 × 2πr2
= 2πr(h + 2r)
= 2 × (22/7) × 3.5 × (10 + 2×3.5)
= (154/7) × (10 + 7)
= 22 × 17
= 374 cm2
Hence,
the total surface area of the article is 374 cm2.
Question 8. A hemispherical and conical hole is scooped out of a solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows :
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm. Give your answer correct to the nearest whole number.
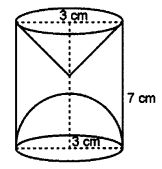
Answer :
Given that :
Radius of each of hemisphere, cone and cylinder (r) = 3 cm
Height of cylinder = 7 cm
Height of cone = 3 cm
Volume of remaining solid = Vol. of cylinder – Vol. of cone – Vol. of hemisphere
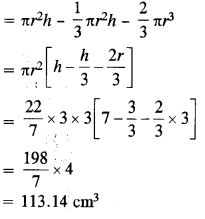
Mensuration Exe-17.4
ML Aggarwal Class 10 ICSE Maths Solutions
Page 424
Question 9. A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. If the total height of the toy is 15.5 cm, find the total surface area of the toy.
Answer :
Total height of the toy = 15.5 cm
Radius of the base of the conical part (r) = 3.5 cm
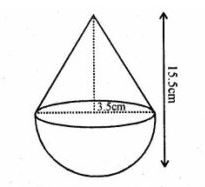
Total height of the toy = 15.5 cm
Height of the cone = 15.5 – 3.5 = 12 cm
Slant height of the cone, l = √(h2 + r2)
l = √(122 + 3.52)
⇒ l = √(144 + 12.25)
⇒ l = √(156.25)
⇒ l = 12.5 cm
Total surface area of the toy = curved surface area of cone + curved surface area of the hemisphere
= πrl + 2πr2
= πr(l + 2r)
= (22/7) × 3.5 × (12.5 + 2 × 3.5)
= (77/7) × (12.5 + 7)
= 11 × 19.5
= 214.5 cm2
Hence
the total surface area of the toy is 214.5 cm2.
Question 10. A circus tent is in the shape of a cylinder surmounted by a cone. The diameter of the cylindrical portion is 24 m and its height is 11 m. If the vertex of the cone is 16 m above the ground, find the area of the canvas used to make the tent.
Answer :
Radius of base of cylindrical portion of tent (r) = 24/2 = 12 m
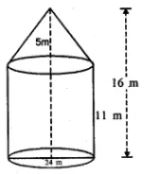
Height of the cylindrical part, H = 11 m
Since vertex of cone is 16 m above the ground, height of cone, h = 16 – 11
h = 5 m
Slant height of the cone, l = √(h2 + r2)
l = √(52 + 122)
⇒ l = √(25 + 144)
⇒ l = √(169)
⇒ l = 13 m
Radius of cone, r = 12 m
Area of canvas used to make the tent = curved surface area of the cylindrical part + curved surface area of the cone.
Area of canvas used to make the tent = 2πrH + πrl
= πr(2H + l)
= (22/7) × 12 × (2 × 11 + 13)
= (264/7) × (22 + 13)
= (264/7) × 35
= 264 × 5
= 1320 m2
Hence,
the area of canvas used to make the tent is 1320 m2.
(ML Aggarwal Mensuration Exe-17.4 Class 10)
Question 11. An exhibition tent is in the form of a cylinder surmounted by a cone. The height of the tent above the ground is 85 m and the height of the cylindrical part is 50 m. If the diameter of the base is 168 m, find the quantity of canvas required to make the tent. Allow 20% extra for folds and stitching. Give your answer to the nearest m².
Answer :
Total height of the tent = 85 m
Height of cylindrical part (h1) = 50 m
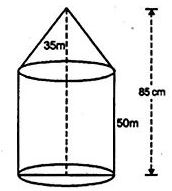
height of the cone, h = 85 – 50
h = 35 m
Diameter of the base, d = 168 m
Radius of the base of cylindrical part, r = d/2 = 168/2 = 84 m
Radius of cone, r = 84 m
Slant height of the cone, l = √(h2 + r2)
l = √(352 + 842)
⇒ l = √(1225 + 7056)
⇒ l = √(8281)
⇒ l = 91 m
Surface area of tent = curved surface area of cylinder + curved surface area of cone
= 2πrH + πrl
= πr(2H + l)
= (22/7) × 84 × (2 × 50 + 91)
= (22/7) × 84 × (100 + 91)
= ((22 × 84)/7) × 191
= (1848/7) × 191
= 264 × 191
= 50424 m2
Adding 20% extra for folds and stitches,
Area of canvas = 50424 + 20% of 50424
= 50424 + (20/100) × 50424
= 50424 + 0.2 × 50424
= 50424 + 10084.8
= 60508.8 m2
= 60509 m2
Hence,
the quantity of canvas required to make the tent is 60509 m2.
Question 12. From a solid cylinder of height 30 cm and radius 7 cm, a conical cavity of height 24 cm and of base radius 7 cm is drilled out. Find the volume and the total surface of the remaining solid.
Answer :
Radius of solid cylinder (r1) = 7 cm
height of the cylinder, H = 30 cm
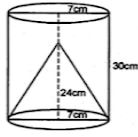
Height of cone, h = 24 cm
Radius of cone, r = 7 cm
Slant height of the cone, l = √(h2 + r2)
l = √(242 + 72)
⇒ l = √(576 + 49)
⇒ l = √(625)
⇒ l = 25 cm
Volume of the remaining solid = Volume of the cylinder – Volume of the cone
= πr2H – (1/3)πr2h
= πr2(H – h/3)
= (22/7) × 72 × (30 – 24/3)
= (22 × 7) × (30 – 8)
= (154) × (22)
= 3388 cm3
Volume of the remaining solid is 3388 cm3.
Total surface area of the remaining solid = Curved surface area of cylinder + surface area of top of the cylinder + curved surface area of the cone
Total surface area of the remaining solid = 2πrH + πr2 + πrl
= πr(2H + r + l)
= (22/7) × 7(2 × 30 + 7 + 25)
= 22 × (60 + 32)
= 22 × 92
= 2024 cm2
Hence, the total surface area of the remaining solid is 2024 cm2.
Question 13. The adjoining figure shows a hemisphere of radius 5 cm surmounted by a right circular cone of base radius 5 cm. Find the volume of the solid if the height of the cone is 7 cm. Give your answer correct to two places of decimal.
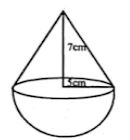
Answer :
Height of the conical part (h) = 7 cm
and radius of the base (r) = 5 cm
Height of the cone, h = 7 cm
Volume of the solid = Volume of the hemisphere + Volume of the cone
= (2/3)πr3 + (1/3)πr2h
= (1/3)πr2(2r + h)
= (1/3) × (22/7) × 52(2×5 + 7)
= (22/21) × 25(10 + 7)
= (22/21) × 25 × 17
= 445.238 cm3
= 445.24 cm3
Hence,
the volume of the solid is 445.24 cm3.
Question 14. A buoy is made in the form of a hemisphere surmounted by a right cone whose circular base coincides with the plane surface of the hemisphere. The radius of the base of the cone is 3.5 metres and its volume is 2/3 of the hemisphere. Calculate the height of the cone and the surface area of the buoy correct to 2 places of decimal
Answer :
Radius of base of hemisphere = 7/2 m
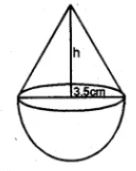
Given radius of the cone, r = 3.5 cm
Radius of hemisphere, r = 3.5 cm = 7/2 cm
Volume of hemisphere = (2/3)πr3
= (2/3) × (22/7) × (7/2)3
= (2/3) × (22/7) × (7/2) × (7/2) × (7/2)
= (22/3) × (7/2) × (7/2)
= 11 × 49/6
= 539/6 m3
Volume of cone = 2/3 of volume of hemisphere
= (2/3) × 539/6
= 539/9 m3
Volume of cone = (1/3)πr2h
(1/3)πr2h = 539/9
⇒ (1/3) × (22/7) × (7/2)2 × h = 539/9
⇒ h = 539 × 3 × 2/9 × 11 × 7
⇒ h = 14/3
⇒ h = 4.667
⇒ h = 4.67 m
Hence, the height of the cone is 4.67 m.
Slant height of cone, l = √(h2 + r2)
= √((14/3)2 + (7/2)2)
= √((196/9) + (49/4))
= √((784/36) + (441/36))
= √(1225/36)
= 35/6 m
= πrl + 2πr2
= πr(l+ 2r)
= (22/7) × (7/2) × ((35/6) + 2 × (7/2))
= 11 × ((35/6) + 7)
= 11 × (5.8333 + 7)
= 11 × (12.8333)
= 141.166 m2
= 141.17 m2
Hence,
the Surface area of the buoy is 141.17 m2.
Question 15. A building is in the form of a cylinder surmounted by a hemisphere valted dome and contains 41 (19/21) m3of air. If the internal diameter of dome is equal to its total height above the floor, find the height of the building.
Answer :
Let the radius of the dome be r.
Internal diameter = 2r
Given internal diameter is equal to total height.
Total height of the building = 2r
Height of the hemispherical area = r
So height of cylindrical area, h = 2r – r = r
Volume of the building = Volume of cylindrical area + volume of hemispherical area
= πr2h + (2/3)πr3
= πr3+ (2/3)πr3 [∵ h = r]
= πr3 (1 + 2/3)
= πr3 (3 + 2)/3
= (5/3)πr3
Given,
Volume of the building = 41(19/21) = 880/21
⇒ (5/3)πr3 = 880/21
⇒ (5/3) × (22/7) × r3 = 880/21
⇒ r3 = 880 × 3 × 7/(5 × 22 × 21)
⇒ r3 = 880/110
⇒ r3 = 8
Taking cube root
r = 2 m
Height of the building = 2r = 2 × 2 = 4 m
Hence
the height of the building is 4 m.
(ML Aggarwal Mensuration Exe-17.4 Class 10)
Question 16. A rocket is in the form of a right circular cylinder closed at the lower end and surmounted by a cone with the same radius as that of the cylinder. The diameter and the height of the cylinder are 6 cm and 12 cm respectively. If the slant height of the conical portion is 5 cm, find the total surface area and the volume of the rocket. (Use π = 3.14).
Answer :
Height of the cylindrical part (A) = 12 cm
Diameter = 6 cm
Radius (r) = 6/2 = 3 cm
Slant height of the conical part (l) = 5 cm
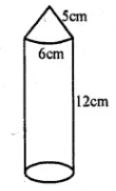
Height of the cone, h = √(l2 – r2)
⇒ h = √(52 – 32)
⇒ h = √(25 – 9)
⇒ h = √16
⇒ h = 4 cm
Total surface area of the rocket = curved surface area of cylinder + base area of cylinder + curved surface area of cone
= 2πrH + πr2 + πrl
= πr(2H + r + l)
= 3.14 × 3 × (2×12 + 3 + 5)
= 3.14 × 3 × (24 + 3 + 5)
= 3.14 × 3 × 32
= 301.44 cm2
Hence, the Total surface area of the rocket is 301.44 cm2.
Volume of the rocket = Volume of the cone + volume of the cylinder
= (1/3)πr2h + πr2H
= πr2((h/3) + H)
= 3.14 × 32 × ((4/3) + 12)
= 3.14 × 9 × ((4 + 36)/3)
= 3.14 × 9 × (40/3)
= 3.14 × 3 × 40
= 376.8 cm3
Hence, the volume of the rocket is 376.8 cm3.
Question 17. The adjoining figure represents a solid consisting of a right circular cylinder with a hemisphere at one end and a cone at the other. Their common radius is 7 cm. The height of the cylinder and the cone are each of 4 cm. Find the volume of the solid.
Answer :
Given common radius, r = 7 cm
Height of the cone, h = 4 cm
Height of the cylinder, H = 4 cm
Volume of the solid = Volume of the cone + Volume of the cylinder + Volume of the hemisphere
= (1/3)πr2h + πr2H + (2/3)πr3
= πr2[(h/3) + H + (2r/3)]
= (22/7) × 72 × [(4/3) + 4 + (2 × 7)/3]
= 22 × 7 × ((4 + 12 + 14)/3)
= 22 × 7 × 30/3
= 1540 cm3
Hence,
the volume of the solid is 1540 cm3.
(ML Aggarwal Mensuration Exe-17.4 Class 10)
Question 18. A solid is in the form of a right circular cylinder with a hemisphere at one end and a cone at the other end. Their common diameter is 3.5 cm and the height of the cylindrical and conical portions are 10 cm and 6 cm respectively. Find the volume of the solid. (Take π = 3.14)
Answer :
Diameter = 3.5 cm
Radius (r) = 3.5/2 = 1.75 cm
Height of cylindrical part (h1) = 10 cm
and height of conical part (h2) = 6 cm
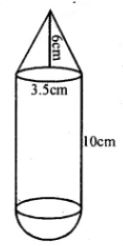
Volume of the solid = Volume of the cone + Volume of the cylinder + Volume of the hemisphere
= (1/3)πr2h + πr2H + (2/3πr3
= πr2((h/3) + H + (2r/3))
= 3.14 × 1.752 × ((6/3) + 10 + (2 × 1.75)/3)
= 3.14 × 3.0625 × (2 + 10 + 1.167)
= 3.14 × 3.0625 × 13.167
= 9.61625 × 13.167
= 126.617 cm3
= 126.62 cm3
Hence,
the volume of the solid is 126.62 cm3.
Mensuration Exe-17.4
ML Aggarwal Class 10 ICSE Maths Solutions
Page 425
Question 19. A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The height and radius of the cylindrical part are 13 cm and 5 cm respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Calculate the surface area of the toy if the height of the conical part is 12 cm.
Answer :
Height of cylindrical part = 13 cm
Radius = 5 cm
Radius of cone (r) = 5 cm
Height of cone (h) = 12 cm
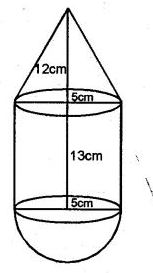
Slant height of the cone, l = √(h2 + r2)
= √(12)2 + (5)2)
= √(144 + 25)
= √169
= 13 cm
Surface area of the toy = curved surface area of cylinder + curved surface area of hemisphere + curved surface area of cone
= 2πrH + 2πr2 + πrl
= πr(2H + 2r + l)
= (22/7) × 5(2×13 + 2×5 + 13)
= (110/7) × (26 + 10 + 13)
= (110/7) × 49
= 110 × 7
= 770 cm2
Hence
the surface area of the toy is 770 cm2.
(ML Aggarwal Mensuration Exe-17.4 Class 10)
Question 20. The adjoining figure shows a model of a solid consisting of a cylinder surmounted by a hemisphere at one end. If the model is drawn to a scale of 1 : 200, find:
(i) the total surface area of the solid in π m².
(ii) the volume of the solid in π litres.
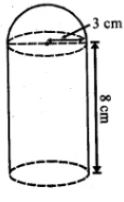
Answer :
(i) In the given figure,
Height of cylindrical portion (h) = 8 cm
Radius (r) = 3 cm
Scale = 1 : 200
Total surface area = 2πr2 + 2πrh
= 2πr(r + h) cm2
= 2 × π × 3[3 + 8] cm2
= 6π × 11
= 66π cm2
∴ Surface area of the solid = 66π × (200)2/1 cm2
= 66π × 40000 cm2
= (66 × 40000)/(100 × 100) π
= 264π m2
(ii) And volume in = π litres (of model)
= 2/3 πr3 + πr2h
= πr2 (2/3r + h) cm3
= π × (3)2 (2/3 × 3 + 8) cm3
= 9π (2 + 8)
= 90π cm3
Scale = 1 : 200
∴ Capacity = 90π × (200)3 cm3
= 90π × 8000000 cm3
= 720000000π cm3
= (720000000π)/(100 × 100 × 100)
= 720π m3
= 720 π × 1000 litres
= 720000π litres
–: End of ML Aggarwal Mensuration Exe-17.4 Class 10 ICSE Maths Solutions :–
Return to :- ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends


