ML Aggarwal Measures of Central Tendency Exe-21.2 Class 10 ICSE Maths Solutions. We Provide Step by Step Answer of Exe-21.2 Questions for Measures of Central Tendency as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Measures of Central Tendency Exe-21.2 Class 10 ICSE Maths Solutions
| Board | ICSE |
| Subject | Maths |
| Class | 10th |
| Chapter-21 | Measures of Central Tendency |
| Writer / Book | Understanding |
| Topics | Solutions of Exe-21.2 |
| Academic Session | 2024-2025 |
Measures of Central Tendency Exe-21.2
ML Aggarwal Class 10 ICSE Maths Solutions
Page 499
Question 1. A student scored the following marks in 11 questions of a question paper : 3, 4, 7, 2, 5, 6, 1, 8, 2, 5, 7 Find the median marks.
Answer :
Arranging in the ascending order, 1, 2, 2, 3, 4, 5, 5, 6, 7, 7, 8
Here, n = 11 i.e. odd,
The middle term = (n+1)\2 = (11+1)\2 = 12\6 = 6th term
Median = 5
Question 2. For the following set of the number, find the median :
10, 75, 3, 81, 17, 27, 4, 48, 12, 47, 9, 15
Answer :
On arranging in ascending order 3, 4, 9, 10, 12, 15, 17, 27, 47, 48, 75, 81
Here, n = 12 which is even
Therefore, median = {(n/2)th term + (n/2 + 1)th term}/2
= {(12/2)th term + (12/2 + 1)th term}/2
= (6th term + 7th term)/2
= (15 + 17)/2 = 32/2 = 16
Median = 16.
Question 3. Calculate the mean and the median of the numbers : 2, 1, 0, 3, 1, 2, 3, 4, 3, 5
Answer :
Writing in ascending order 0, 1, 1, 2, 2, 3, 3, 3, 4, 5
Here, n = 10 which is even
Median = ½ ( n/2 th term + ((n/2) + 1)th term)
= ½ (10/2 th term + ((10/2) + 1)th term)
= ½ (5 th term + (5 + 1)th term)
= ½ (5 th term + 6th term)
= ½ (2 + 3)
= ½ × 5
= 2.5
Hence, the median is 2.5.
Mean = sum of the observations/number of observations
= Ʃxi/n
= (0 + 1 + 1 + 2 + 2 + 3 + 3 + 3 + 4 + 5)/10
= 24/10
= 2.4
Hence, the mean is 2.4.
Question 4. The median of the observations 11, 12, 14, (x – 2), (x + 4), (x + 9), 32, 38, 47 arranged in ascending order is 24. Find the value of x and hence find the mean.
Answer :
Observation are :
11, 12, 14, (x – 2), (x + 4), (x + 9), 32, 38, 47
n = 9
Median = (9+1)\2 th term
i.e, 5th term = x + 4
median = 24
x + 4 = 24
⇒ x = 24 – 4 = 20
Sum of observations = 11 + 12 + 14 + (x – 2) + (x + 4) + (x + 9) + 32 + 38 + 47
= 165 + 3x
Substitute x = 20
Sum of observations = 165 + 3 × 20
= 165 + 60
= 225
Mean = Sum of observations /number of observations
= 225/9 = 25
Question 5. The mean of the numbers 1, 7, 5, 3, 4, 4, is m. The numbers 3, 2, 4, 2, 3, 3, p have mean m – 1 and median q. Find
(i) p
(ii) q
(iii) the mean of p and q.
Answer :
(i) Mean of 1, 7, 5, 3, 4, 4 is m.
Here n = 6
Mean, m = (1 + 7 + 5 + 3 + 4 + 4)/6
⇒ m = 24/6
⇒ m = 4
Given the numbers 3, 2, 4, 2, 3, 3, p have mean m-1.
So,
m-1 = (3 + 2 + 4 + 2 + 3 + 3 + p)/7
⇒ 4 – 1 = (17 + p)/7
⇒ 3 = (17 + p)/7
⇒ 3 × 7 = 17 + p
⇒ 21 = 17 + p
⇒ p = 21 – 17
p = 4
Hence, the value of p is 4.
(ii) Given the numbers have median q.
Arranging them in ascending order
2, 2, 3, 3, 3, 4, 4
Here n = 7 which is odd
So, median = ((n + 1)/2)th term
⇒ q = ((7 + 1)/2)th term
⇒ q = (8/2)th term
⇒ q = 4th term
⇒ q = 3
So, value of q is 3.
(iii) mean of p and q = (p + q)/2
= (4 + 3)/2
= 7/2
= 3.5
Question 6. Find the median for the following distribution:

Answer :
Writing the distribution in cumulative frequency table:
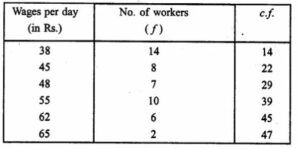
Here total number of observations, n = 47 which is odd.
So median = ((n + 1)/2)th term
= ((47 + 1)/2)th term
= (48/2)th term
= 24th term
= 48 [Since, 23rd to 29th observation is 48]
Measures of Central Tendency Exe-21.2
ML Aggarwal Class 10 ICSE Maths Solutions
Page 500
Question 7. Marks obtained by 70 students are given below :

Calculate the median marks.
Answer :
Arranging the variates in ascending order and in c.f. table.
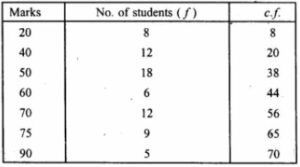
Median = ½ ( n/2th term + ((n/2)+1)th term)
Here, total number of observations, n = 70 which is even.
= ½ (70/2th term + ((70/2)+1)th term)
= ½ (35th term + (35+1)th term)
= ½ (35th term + 36th term)
= ½ (50 + 50) [Since all observations from 21st to 38th are 50]
= ½ ×100
= 50
Question 8. Calculate the mean and the median for the following distribution :

Answer :
Writing the distribution in c.f. table :

Mean = Ʃfx/Ʃf
= 390/20
= 19.5
Hence the mean is 19.5.
Here number of observations, n = 20 which is even.
So median = = ½ (n/2 th term + ((n/2) + 1)th term)
= ½ (20/2 th term + ((20/2) + 1)th term)
= ½ (10 th term + (10 + 1)th term)
= ½ (10 th term + 11th term)
= ½ (20+20) [Since all observations from 9th to 14th are 20]
= ½ ×140
= 20
Question 9.
The daily wages (in rupees) of 19 workers are
41, 21, 38, 27, 31, 45, 23, 26, 29, 30, 28, 25, 35, 42, 47, 53, 29, 31, 35.
Find
(i) the median
(ii) lower quartile
(iii) upper quartile range,
(iv) interquartile range.
Answer :
Arranging the observations in ascending order
21, 23, 25, 26, 27, 28, 29, 29, 30, 31, 31, 35, 35, 38, 41, 42, 45, 47, 53
Here n = 19 which is odd.
(i) Median = ((n + 1)/2)th term
= (19 + 1)/2
= 20/2
= 10th term
= 31
(ii) Lower quartile, Q1 = ((n + 1)/4) th term
= (19 + 1)/4
= 20/4
= 5th term
= 27
(iii) Upper quartile, Q3 = (3(n + 1)/4)th term
= (3 × (19 + 1)/4)th term
= (3 × (20/4))th term
= (3 × 5)th term
= 15 th term
= 41
(iv) Interquartile range = Q3 – Q1
= 41 – 27
= 14
Question 10. From the following frequency distribution, find :
(i) the median
(ii) lower quartile
(iii) upper quartile
(iv) inter quartile range

Answer :
Writing frequency distribution in c.f. table :

So median = ½ (n/2th term + ((n/2) + 1)th term)
(i) Here number of observations, n = 48 which is even.
= ½ (48/2th term + ((48/2) + 1)th term)
= ½ (24th term + (24 + 1)th term)
= ½ (24th term + 25th term)
= ½ (22 + 22) [Since all observations from 19th to 27th are 22]
= ½ × 44
= 22
Hence, the median is 22.
(ii) Lower quartile, Q1 = (n/4)th term
= (48)/4
= 12th term
= 20
Hence the lower quartile is 20.
(iii) Upper quartile, Q3 = (3n/4)th term
= (3 × 48/4)th term
= (3 × 12)th term
= 36th term
= 27
Hence the upper quartile is 27.
(iv) Interquartile range = Q3 – Q1
= 27 – 20
= 7
Hence, the Interquartile range is 7.
Question 11. For the following frequency distribution, find :
(i) the median
(ii) lower quartile
(iii) upper quartile

Answer :
Writing the distribution in cumulative frequency (c.f.) table :

(i) Here number of observations, n = 63 which is odd.
Median = ((n + 1)/2)th term
= (63 + 1)/2
= 64/2
= 32th term
= 40
(ii) Lower quartile, Q1 = ((n + 1)/4) th term
= (63 + 1)/4
= 64/4
= 16th term
= 34
(iii) Upper quartile, Q3 = (3(n + 1)/4)th term
= (3 × (63 + 1)/4)th term
= (3 × (64/4))th term
= (3 × 16)th term
= 48th term
= 48
-: End of ML Aggarwal Measures of Central Tendency Exe-21.2 Class 10 ICSE Maths Solutions :–
Return to :- ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends


