ML Aggarwal Measures of Central Tendency Exe-21.3 Class 10 ICSE Maths Solutions. We Provide Step by Step Answer of Exe-21.3 Questions for Measures of Central Tendency as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Measures of Central Tendency Exe-21.3 Class 10 ICSE Maths Solutions
| Board | ICSE |
| Subject | Maths |
| Class | 10th |
| Chapter-21 | Measures of Central Tendency |
| Writer / Book | Understanding |
| Topics | Solutions of Exe-21.3 |
| Academic Session | 2024-2025 |
Measures of Central Tendency Exe-21.3
ML Aggarwal Class 10 ICSE Maths Solutions
Question 1. Find the mode of the following sets of numbers ;
(i) 5, 7, 6, 8, 9, 0, 6, 8, 1, 8
(ii) 9, 0, 2, 8, 5, 3, 5, 4, 1, 5, 2, 7
Answer :
(i) ∵ The number 8 occurs maximum times
Mode = 8
(ii) ∵ The number 5, occurs maximum times
Mode = 5
Question 2. Find the mean, median and mode of the following distribution : 8, 10, 7, 6, 10, 11, 6, 13, 10
Answer :
Mean =
= 81/9 = 9
Given nos. in ascending order are as follows:
6, 6, 7, 8, 10, 10, 10, 11, 13
Median = (n+1)\2 th term = (9+1)\2 = 5th term = 10
Mode = 10 (having highest frequency 3 times)
Question 3. Calculate the mean, the median and the mode of the following numbers : 3, 1, 5, 6, 3, 4, 5, 3, 7, 2
Answer :
Arranging in ascending order 1, 2, 3, 3, 3, 4, 5, 5, 6, 7
Mean = Ʃxi/n
= (1 + 2 + 3 + 3 + 3 + 4 + 5 + 5 + 6 + 7)/10
= 39/10
= 3.9
Here number of observations, n = 10 which is even.
So median = ½ (n/2th term + ((n/2) + 1)th term)
= ½ (10/2th term + ((10/2) + 1)th term)
= ½ (5th term + (5 + 1)th term)
= ½ (5th term + 6th term)
= ½ (3 + 4)
= ½ × 7
= 3.5
In the given set, 3 occurs maximum number of times.
Hence,
the mode is 3.
Question 4. The marks of 10 students of a class in an examination arranged in ascending order are as follows: 13, 35, 43, 46, x, x +4, 55, 61,71, 80
If the median marks is 48, find the value of x. Hence, find the mode of the given data. (2017)
Answer :
Given marks are 13, 35, 43, 46, x, x + 4, 55, 61, 71, 80
n = 10 (even), median = 48
median = ½ (n/2th term + ((n/2) + 1)th term)
48 = ½ (10/2th term + ((10/2) + 1)th term)
⇒ 48 = ½ (5th term + (5 + 1)th term)
⇒ 48 = ½ (5th term + 6th term)
⇒ 48 = ½ (x + x + 4)
⇒ 48 = ½ × (2x + 4)
⇒ 48 = x + 2
⇒ x = 48 – 2 = 46
⇒ x + 4 = 46 + 4 = 50
So the distribution becomes
13, 35, 43, 46, 46, 50, 55, 61, 71, 80
Here, 46 occurs maximum number of times.
Hence, the mode is 46.
Question 5. Find the mode and median of the following frequency distribution :
![]()
Answer :

Question 6. In a class of 40 students, marks obtained by the students in a class test (out of 10) are given below:

Calculate the following for the given distribution :
(i) Median
(ii) Mode
Answer :

Here,
Marks corresponding to cumulative frequency 20 is 6
Thus, the required median is 6.
Clearly, 6 occurs 10 times which is maximum.
Hence, mode is 6.
Measures of Central Tendency Exe-21.3
ML Aggarwal Class 10 ICSE Maths Solutions
Page 503
Question 7. The marks obtained by 30 students in a class assessment of 5 marks is given below:

Calculate the mean, median and mode of the above distribution.
Answer :
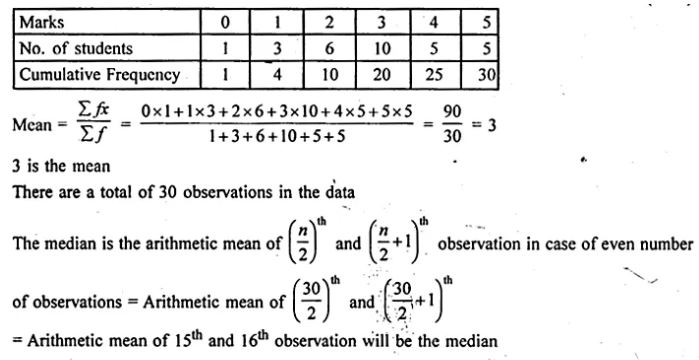
= ½ (3 + 3)
= 6/2
= 3
Hence, the median is 3.
Here, the mark 3 occurs maximum number of times.
Hence, the mode is 3.
Question 8. The distribution given below shows the marks obtained by 25 students in an aptitude test. Find the mean, median and mode of the distribution.

Answer :
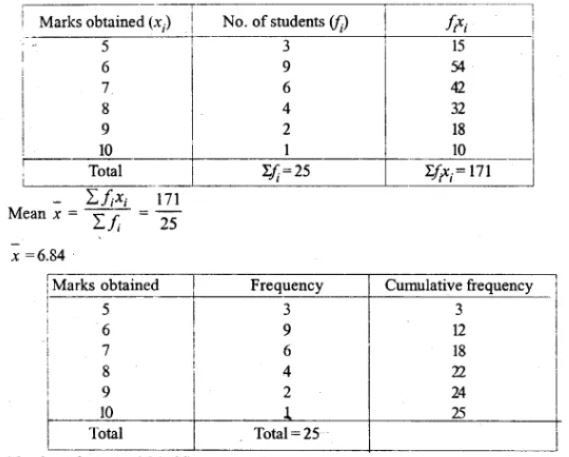
n = 25 which is odd.
Median = ((n + 1)/2)th term
= (25 + 1)/2
= 26/2
= 13th term
= 7
Hence, the median is 7.
Here, the frequency corresponding to 6 is maximum.
Hence,
the mode is 6.
Question 9. The following table gives the weekly wages (in Rs.) of workers in a factory :

Calculate:
(i) The mean.
(ii) the modal class
(iii) the number of workers getting weekly wages below Rs. 80.
(iv) the number of workers getting Rs. 65 or more but less than Rs. 85 as weekly wages.
Answer :
Representing the given distribution in cumulative frequency distribution
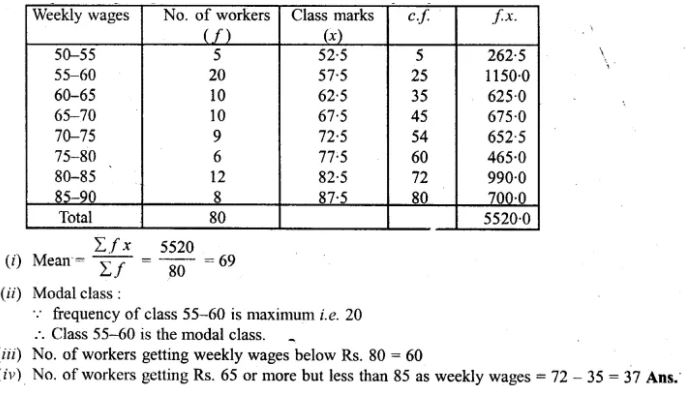
-: End of ML Aggarwal Measures of Central Tendency Exe-21.3 Class 10 ICSE Maths Solutions :–
Return to :- ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends


