Expansions ICSE Class-9th Concise Selina Mathematics

Expansions ICSE Class-9th Concise Selina Mathematics Solutions (Including Substitution) Chapter-4. We provide step by step Solutions of Exercise / lesson-4 Expansions (Including Substitution) for ICSE Class-9 Concise Selina Mathematics by RK Bansal.

Our Solutions contain all type Questions with Exe-4 A, Exe-4 B, Exe-4 C, Exe-4 D and Exe-4 E to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-9 Mathematics .

Expansions ICSE Class-9th Concise Selina Mathematics Solutions (Including Substitution) Chapter-4

---

–: Select Topics :–

 

Exe-4 A,

Exe-4 B,

Exe-4 C,

Exe-4 D,

 

---

Exercise – 4(A) Expansions (Including Substitution) ICSE Class-9th Concise Selina Mathematics

Question 1.1

Answer 

We Know that
( a + b )2 = a2 + b2 + 2ab
(2a + b)2 = 4a2 + b2 + 2 x 2a x b
= 4a2 + b2 + 4ab

Question 1.2

Answer 

We know that
( a + b )² = a² + b² + 2ab
( 3a + 7b )² = 9a² + 49b² + 2 x 3a x 7b
= 9a² + 49b² + 42ab

Question 1.3

Answer 

We know that
( a – b )² = a² + b² – 2ab
( 3a – 4b )² = 9a² + 16b² – 2 x 3a x 4b
= 9a² + 16b² – 24ab

Question 1.4

Find the square of : ……….

Answer 

We know that,
( a – b )2 = a2 + b2 – 2a

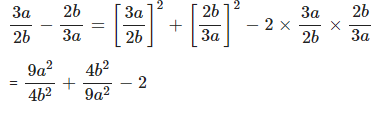
Question 2.1

Answer 

(101)²
(101)² = (100 + 1)²
We know that,
(a + b)² = a² + b² + 2ab
∴ (100 + 1)² = 100² + 1² + 2 x 100 x 1
= 10,000 + 1 + 200
= 10,201

Question 2.2

Answer 

(502)²
(502)² = (500 + 2)²
We know that,
( a + b )² = a² + b² + 2ab
∴ ( 500 + 2 )² = 500² + 2² + 2 x 500 x 2
= 250000 + 4 + 2000
= 2,52,004

Question 2.3

Answer 

(97)²
(97)² = (100 – 3)²
We know that,
( a – b )² = a² + b² – 2ab
∴ (100 – 3)² = 100² + 3² – 2 x 100 x 3
= 10000 + 9 – 600
= 9,409

Question 2.4

Answer 

(998)²
(998)² = (1000 – 2)²
We know that
( a – b )² = a² + b² – 2ab
∴ (1000 – 2)² = 1000² + 2² – 2 x 1000 x 2
= 1000000 + 4 – 4000
= 9,96,004

Question 3.1

Evalute : …………

Answer 

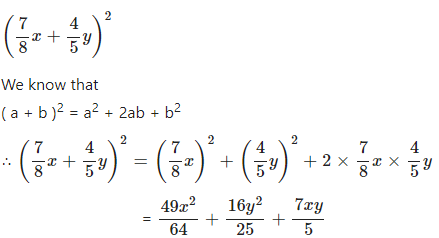
Question 3.2

Evalute :………….

Answer 

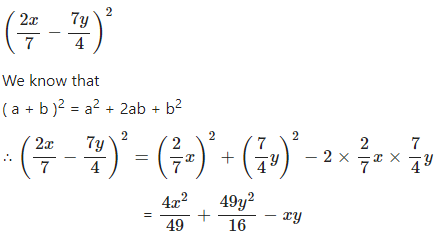
Question 4.1

Evaluate :…………..

Answer 

Consider the given expression :

 

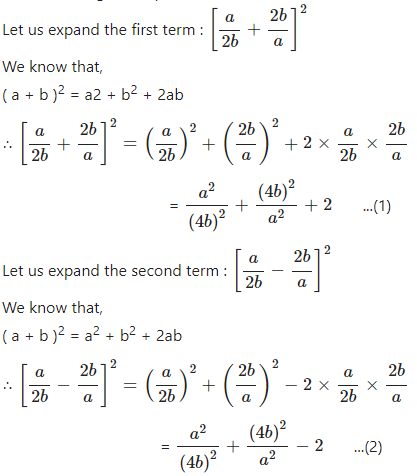
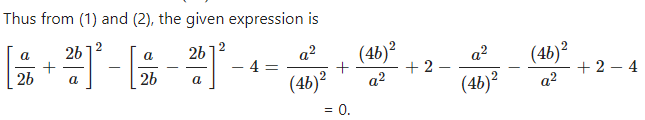
Question 4.2

Answer 

Question 5

Answer 

Question 6

Answer 

We know that,
( a – b )² = a² – 2ab + b²
and
( a + b )² = a² + 2ab + b²
Rewrite the above equation, we have
( a + b )² = a²  + b² – 2ab + 4ab
= ( a + b )² + 4ab              …(1)
Given that a – b = 7; ab = 18
Substitute the values of ( a – b ) and (ab)
in equation (1), we have
( a + b )² = (7)² + 4(18)
= 49 + 72 = 121
⇒ a + b = $\pm \sqrt{121}$

⇒ a + b = $\pm 11$

Question 7

If x + y = $\frac{7}{2}\text{and xy}=\frac{\mathrm{5/}}{2}$  ; find :  x – y  and x² – y²

Answer 

We know that,
( x + y )² = x² + 2xy + y²
and
( x – y )² = x² – 2xy + y²
Rewrite the above equation, we have
( x – y )² = x²  + y² + 2xy – 4xy
= ( x + y )² – 4xy              …(1)

 

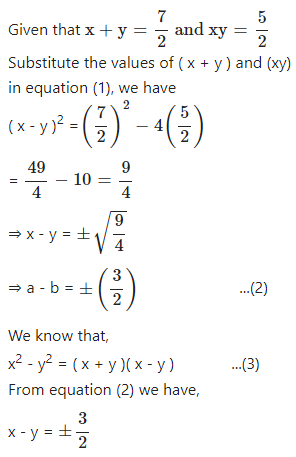
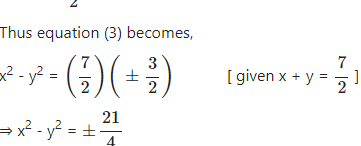
Question 8

If a – b = 0.9 and ab = 0.36; find:
(i) a + b
(ii) a² – b²

Answer 

(i) We know that,
( a – b )² = a² – 2ab + b²
and
( a + b )² = a² + 2ab + b²
Rewrite the above equation, we have
( a + b )² = a²  + b² – 2ab + 4ab
= ( a – b )² + 4ab              …(1)
Given that a – b = 0.9 ; ab = 0.36
Substitute the values of ( a – b ) and (ab)
in equation (1), we have
( a + b )² = ( 0.9 )² + 4( 0.36 )

= 0.81 + 1.44 = 2.25
⇒ a + b = $\pm \sqrt{2.25}$
⇒ a + b = $\pm 1.5$                        ..(2)

(ii) We know that,
a² – b² = ( a + b )( a – b )             ….(3)
From equation (2) we have,
a + b = $\pm$1.5
Thus equation (3) becomes,
a² – b² = $(\pm 1.5)\left(0.9\right)$                [ given a – b = 0.9 ]
⇒ a² – b² = $\pm$1.35

Question 9

If a – b = 4 and a + b = 6; find
(i) a² + b²
(ii) ab

Answer 

(i) We know that,
( a – b )² = a² – 2ab + b²
Rewrite the above identity as,
a²  + b² = ( a – b ) + 2ab           ….(1)
Similarly, we know that,
( a + b )² = a² + 2ab + b²
Rewrite the above identity as,
a²  + b² = ( a + b )² – 2ab                                     …..(2)
Adding the equations (1) and (2), we have
2( a² + b² ) = ( a – b )² + 2ab + ( a + b )² – 2ab
⇒ 2( a² + b² ) = ( a – b )²  + ( a + b )²

⇒ ( a² + b² ) = 26                                            …..(4)

From equation (4), we have
a2 + b2 = 26
Consider the identity,
( a – b )2 = a2 + b2 – 2ab                                ….(5)
Substitute the value a – b = 4 and a2 + b2 = 26
in the above equation, we have
(4)2 = 26 – 2ab
⇒ 2ab = 26 – 16
⇒  2ab = 10

ab=5

Question 10

If a + $\frac{\mathrm{1/}}{a}$= 6 and  a ≠ 0 find :

(i) a….

Answer 

We know that,
( a + b )² = a² + 2ab + b²
and
( a – b )² = a² – 2ab + b² 
Thus,

 

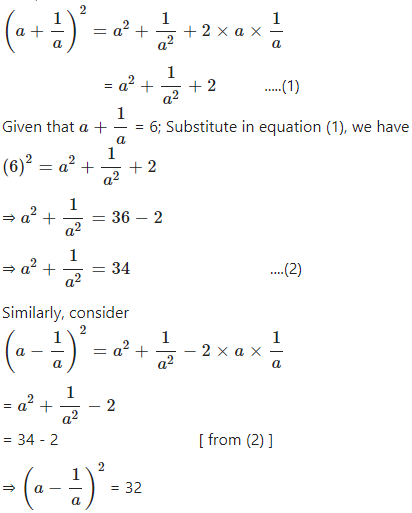
Question 11

If a………….find :

(i) a….

Answer 

We know that,
( a + b )² = a² + 2ab + b²
and
( a – b )² = a² – 2ab + b² 
Thus,

Question 12

If a² – 3a + 1 = 0, and a ≠ 0; find :

Answer 

(i) Consider the given equation
a² – 3a + 1 = 0
Rewrite the given equation, we have

 

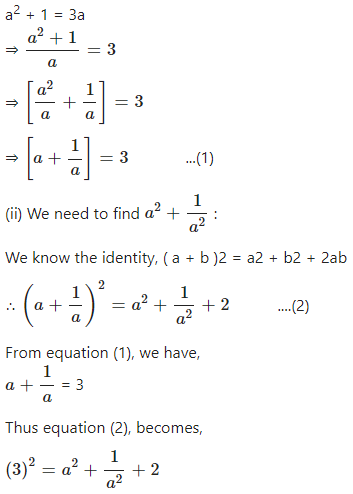
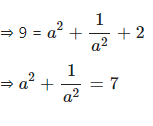
Question 13

If a² – 5a – 1 = 0 and a ≠ 0 ; find :
(i) ………
(ii) …………

(iii) ………..

Answer 

(i) Consider the given equation
a2 – 5a – 1 = 0
Rewrite the given equation, we have
a2 – 1 = 5a

 

Question 14

Answer 

Given that ( 3x + 4y ) = 16 and xy = 4
We need to find 9x² + 16y².
We know that
( a + b )² = a² + b² + 2ab
Consider the square of 3x + 4y :
∴ ( 3x + 4y )² = (3x)² + (4y)² + 2 x 3x x 4y
⇒ ( 3x + 4y )² = 9x² + 16y² + 24xy         …..(1)

Substitute the values of ( 3x + 4y ) and xy
in the above equation (1), we have
( 3x + 4y )² = 9x² + 16y² + 24xy

⇒ (16)² = 9x² + 16y² + 24(4)

⇒ 256 = 9x² + 16y² + 96

⇒ 9x² + 16y² = 160

 

Question 15

Answer 

Given x is 2 more than y, so x = y + 2
Sum of squares of x and y is 34, so x² + y² = 34.
Replace x = y + 2 in the above equation and solve for y.
We get (y + 2)² + y² = 34

2y² + 4y – 30 = 0
y² + 2y – 15 = 0
(y + 5)(y – 3) = 0
So y = -5 or 3
For y = -5, x =-3
For y = 3, x = 5
Product of x and y is 15 in both cases.

Question 16

Answer 

Let the two positive numbers be a and b.
Given difference between them is 5 and sum of squares is 73.

So a – b = 5, a² + b² = 73
Squaring on both sides gives
(a – b)² = 5²
a² + b² – 2ab = 25
but a² + b² = 73
so 2ab = 73 – 25 = 48
ab = 24
So, the product of numbers is 24.

---

Expansions (Including Substitution) Exe-4 B for ICSE Class-9th Concise Selina Mathematics

Question 1.1

Answer 

( a – b )³ = a³ – 3ab( a – b ) – b³
( 3a – 2b )³ = (3a)³ – 3 x 3a x 2b( 3a – 2b) – (2b)³
= 27a³ – 18ab( 3a – 2b ) – 8b³
= 27a³ – 54a²b + 36ab² – 8b³

 

Question 1.2

Answer 

( a + b )³ = a³ + 3ab( a + b ) + b³
( 5a + 3b)³ = (5a)³ + 3 x 5a x 3b( 5a + 3b) + (3b)³
= 125a³ + 45ab( 5a + 3b ) + 27b³
= 125a³ + 225a²b + 135ab² + 27b³ 

Question 1.3

Find the cube of : $2a+\dots \dots \dots \dots ..$

Answer 

( a + b )3 = a3 + 3ab( a + b ) + b3

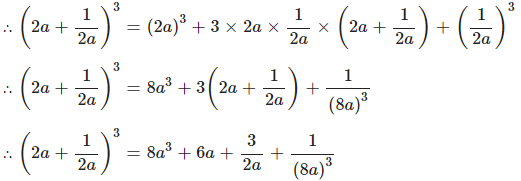
Question 1.4

Find the cube of : $(3\mathrm{a\dots \dots \dots .}$

Answer 

( a – b )³ = a³ – 3ab( a – b ) – b³

 

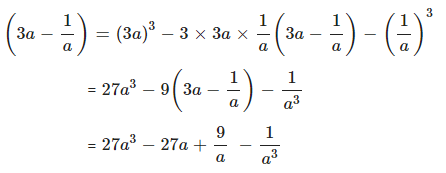
Question 2

Answer 

 

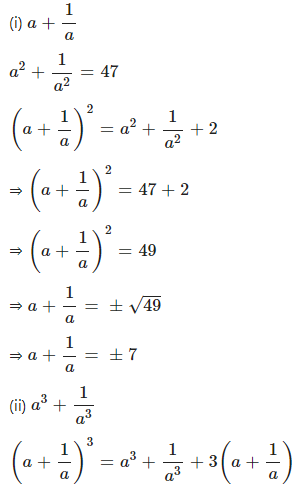
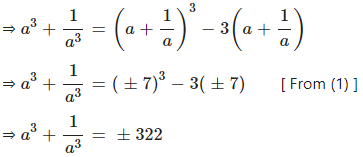
Question 3

Answer 

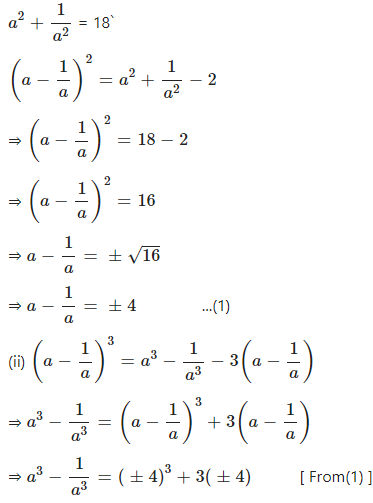
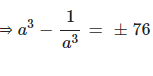
Question 4

If $a+\dots \dots \dots ..$ ; then show that

…………

Answer 

 

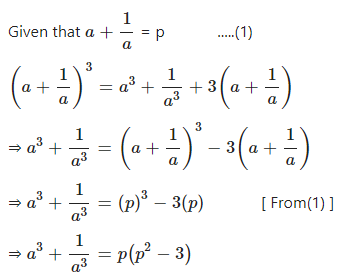
Question 5

Answer 

Question 6

If ${(a+\dots \dots \dots \dots \dots \dots \dots ..}^{}$

Answer 

 

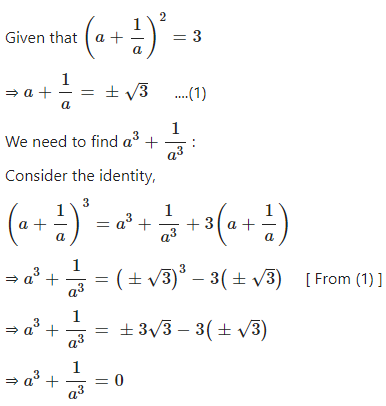
Question 7

Answer 

Given that a + 2b + c = 0;
⇒ a + 2b = -c          ….(1)
Now consider the expansion of ( a + 2b )³ :
( a + 2b )³ = ( – c )³
a³ + (2b)³ + 3 x a x 2b x ( a + 2b ) = -c³

⇒         a³ + 8b³ + 3 x a x 2b x (-c) = -c³          [ from (1) ]

⇒                           a³ + 8b³ – 6abc = -c³ 

⇒                              a³ + 8b³ – c³ = 6abc

Hence proved.

 

Question 8.1

Answer 

Property is if a + b + c = 0 then a³ + b³ + c³ = 3abc
a = 13, b = -8 and c = -5
13³ + (-8)³ + (-5)³ = 3(13)(-8)(-5) = 1560

 

Question 8.2

Answer 

Property is if a + b + c = 0 then a³ + b³ + c³ = 3abc
a = 7, b = 3, c = -10
7³ + 3³ + (-10)³ = 3(7)(3)(-10) = -630

 

Question 8.3

Answer 

Property is if a + b + c = 0 then a³ + b³ + c³ = 3abc
a = 9, b = -5, c = -4
9³ – 5³ – 4³ = 9³ + (-5)³ + (-4)³ = 3(9)(-5)(-4) = 540

 

Question 8.4

Answer 

Property is if a + b + c = 0 then a3 + b3 + c3 = 3abc
a = 38, b = -26, c = -12
383 + (-26)3 + (-12)3 = 3(38)(-26)(-12) = 35568

 

 

Question 9.1

If a ≠ 0 and $\mathrm{a\dots \dots \dots \dots ..}$= 3 ; find :

…………

Answer 

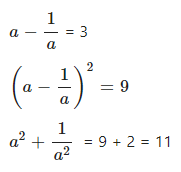
Question 9.2

If a ≠ 0 and …….. 3 ; Find :

…………

Answer 

 

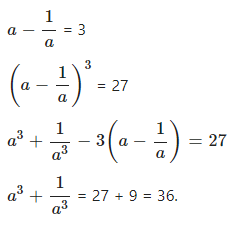
Question 10.1

If a ≠ 0 and $\mathrm{a\dots \dots \dots \dots \dots ..}$= 4 ; find : ………

Answer 

 

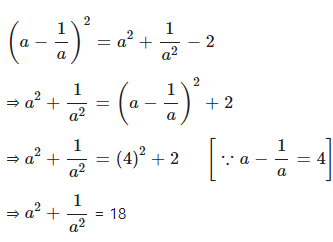
Question 10.2

If a ≠ 0 and $\mathrm{a\dots \dots \dots \dots \dots ..}$= 4 ; find : ………

Answer 

 

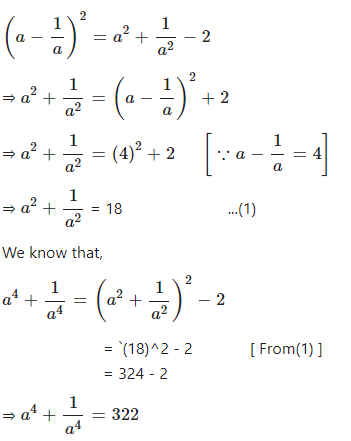
Question 10.3

If a ≠ 0 and $\mathrm{a\dots \dots \dots \dots \dots ..}$= 4 ; find : ………

Answer 

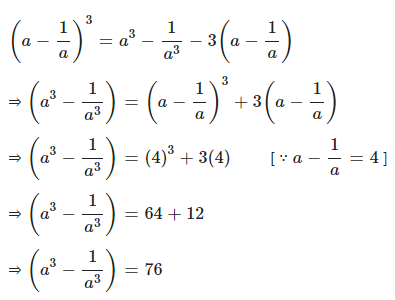
Question 11

If X ≠ 0 and X + ………; then show that :

……….

Answer 

 

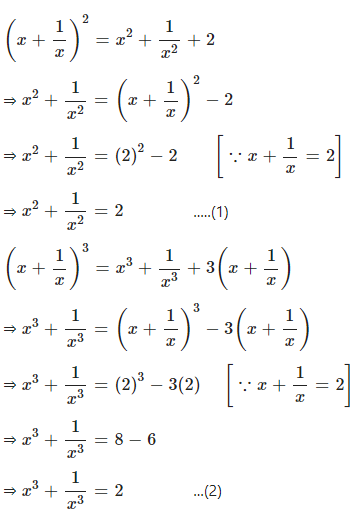
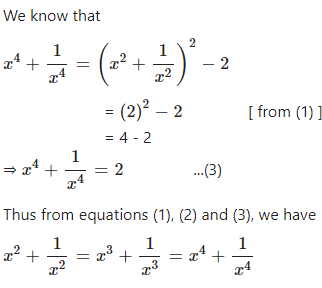
Question 12

Answer 

Given that 2x – 3y = 10, xy = 16

∴ (2x – 3y)³ = (10)³

⇒ 8x³ – 27y³ – 3 (2x) (3y) (2x – 3y) = 1000

⇒ 8x³ – 27 y³ -18xy (2x – 3y) = 1000

⇒ 8x³ – 27 y³ – 18 (16) (10)  = 1000

⇒ 8x³ – 27 y³ – 2880 = 1000

⇒8x³ – 27 y³ = 1000 + 2880

⇒ 8x³ – 27 y³ =3880

 

Question 13.1

Answer 

Question 13.2

Answer 

(3x – 5y – 2z) (3x – 5y + 2z)

= {(3x – 5y) – (2z)} {(3x – 5y) + (2z)}

= (3x – 5y)² – (2z)²{since(a + b) (a – b) = a² – b²}

= 9x² + 25y² – 2 × 3x × 5y – 4z²

= 9x² + 25y²– 30xy – 4z²

= 9x² +25y² – 4z² – 30xy

 

Question 14

Answer 

Given sum of two numbers is 9 and their product is 20.
Let the numbers be a and b.
a + b = 9
ab = 20

Squaring on both sides gives
(a+b)² = 9²
a² + b² + 2ab = 81
a² + b² + 40 = 81
So sum of squares is 81 – 40 = 41

Cubing on both sides gives
(a + b)³ = 9³
a³ + b³ + 3ab(a + b) = 729
a³ + b³ + 60(9) = 729
a³ + b³ = 729 – 540 = 189
So the sum of cubes is 189.

 

Question 15

Two positive numbers x and y are such that x > y. If the difference of these numbers is 5 and their product is 24, find:
(i) Sum of these numbers
(ii) Difference of their cubes
(iii) Sum of their cubes.

Answer 

Given x – y = 5 and xy = 24 (x>y)
(x + y)² = (x – y)² + 4xy = 25 + 96 = 121
So, x + y = 11; sum of these numbers is 11.

Cubing on both sides gives
(x – y)³ = 5³
x³ – y³ – 3xy(x – y) = 125
x³ – y³ – 72(5) = 125
x³ – y³= 125 + 360 = 485
So, difference of their cubes is 485.

Cubing both sides, we get
(x + y)³ = 11³
x³ + y³ + 3xy(x + y) = 1331
x³ + y³ = 1331 – 72(11) = 1331 – 792 = 539
So, sum of their cubes is 539.

 

Question 16

Answer 

xy = ab                                                   ….(i)

4x² + y² = a                                            ….(ii)

Now, (2x + y)² = (2x)² + 4xy + y²

= 4x² + y² + 4xy

= a + 4b                                                 ….[From (i) and (ii)]

⇒ 2x + y = $\pm \sqrt{a+4b}$

---

Selina Solutions of Expansions (Including Substitution) Exe-4 C for ICSE Class-9th Concise Mathematics

Question 1.1

Answer 

( x + 8 )( x + 10 ) = x² + ( 8 + 10 )x + 8 x 10
= x² + 18x + 80

 

Question 1.2

Answer 

( x + 8 )( x – 10 ) = x² + ( 8 – 10 )x + 8 x (-10)
= x² – 2x – 80

 

Question 1.3

Answer 

( X – 8 ) ( X + 10 ) = X² – ( 8 – 10 )X – 8 x 10
= X² + 2X – 80

Question 1.4

Answer 

( X – 8 )( X – 10 ) = X² – ( 8 + 10 )X + 8 x 10
= X² – 18X + 80

 

Question 2.1

Expand : $(2\mathrm{x\dots \dots \dots .,\dots \dots .}$

Answer 

 

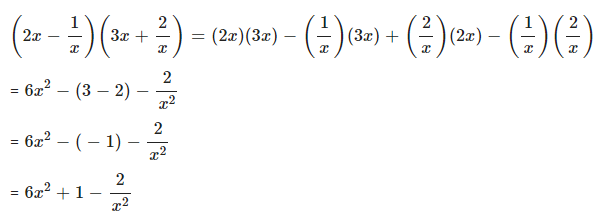
Question 2.2

Expand : $(3\mathrm{a\dots \dots \dots \dots }$

Answer 

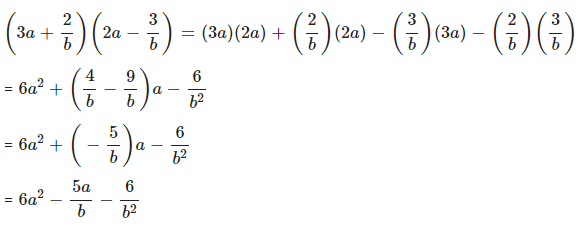
Question 3.1

Expand : ( x + y – z )²

Answer 

( x + y – z )² = x² + y² + z² + 2(x)(y) – 2(y)(z) – 2(z)(x)
= x² + y² + z² + 2xy – 2yz – 2zx

 

Question 3.2

Expand : ( x – 2y + 2 )² 

Answer 

x – 2y + 2 )²  = x² + (2y)² + (2)² – 2(x)(2y) – 2(2y)(2) + 2(2)(x)
= x² + 4y² + 4 – 4xy – 8y + 4x

 

Question 3.3

Expand : ( 5a – 3b + c )²

Answer 

( 5a – 3b + c)² = (5a)² + (3b)² + (c)² – 2(5a)(3b) – 2(3b)(c) + 2(c)(5a)

= 25a² + 9b² + c² – 30ab – 6bc + 10ca

 

Question 3.4

Expand : ( 5x – 3y – 2 )²

Answer 

( 5x – 3y – 2 )² = (5x)² + (3y)² + (2)² – 2(5x)(3y) + 2(3y)(2) – 2(2)(5x)

= 25x² + 9y² + 4 – 30xy + 12y – 20x

 

Question 3.5

Expand : ${(\mathrm{x\dots \dots \dots \dots ..}}^{}$

Answer 

 

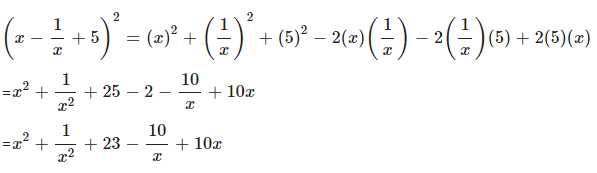
Question 4

Answer 

We know that
( a + b + c )² = a² + b² + c² + 2( ab + bc + ca )       …….(1)
Given that, a² + b² + c² = 50 and a + b + c = 12.
We need to find ab + bc + ca :
Substitute the values of  (a² + b² + c² ) and ( a + b + c )
in the identity (1), we have
(12)² = 50 + 2( ab + bc + ca )

⇒ 144 = 50 + 2( ab + bc + ca )
⇒ 94 = 2( ab + bc + ca)
⇒ ab + bc + ca = $\frac{\mathrm{94/}}{2}$
⇒ ab + bc + ca = 47

 

Question 5

Answer 

We know that
( a + b + c )² = a² + b² + c² + 2( ab + bc + ca )     ….(1)
Given that, a² + b² + c² = 35 and ab + bc + ca = 23
We need to find a + b + c :
Substitute the values of ( a² + b² + c² ) and ( ab + bc + ca )
in the identity (1), we have
( a + b + c )² = 35 + 2(23)
⇒ ( a + b + c )² = 81
⇒ a + b + c = $\pm \sqrt{81}$
⇒ a + b + c = $\pm 9$

 

Question 6

Answer 

We know that
( a + b + c )² = a² + b² + c² + 2( ab + bc + ca )    …..(1)
Given that, a + b + c = p and ab + bc + ca = q
We need to find a² + b² + c² :
Substitute the values of ( ab + bc + ca ) and ( a + b + c )
in the identity (1), we have
(p)² = a² + b² + c² + 2q
⇒ p² = a² + b² + c² + 2q
⇒ a² + b² + c² = p² – 2q

 

Question 7

Answer 

a² + b² + c² = 50 and ab + bc + ca = 47
Since ( a + b + c )² = a² + b² + c² + 2( ab + bc + ca )
∴ ( a + b + c )² = 50 + 2(47)
⇒ ( a + b + c )² = 50 + 94 = 144
⇒ a + b +c = $\sqrt{144}=\pm 12$
∴ a + b + c = $\pm 12$

 

Question 8

Answer 

x + y – z = 4 and x² + y² + z² = 30
Since ( x + y – z)2 = x2 + y2 + z2 + 2( xy – yz – zx ), we have
(4)2 = 30 + 2( xy – yz – zx )
⇒ 16 = 30 + 2( xy – yz – zx )
⇒ 2( xy – yz – zx ) = -14
⇒ xy – yz – zx = $-\frac{\mathrm{14/}}{\mathrm{2= \; -7}}$
∴ xy – yz – zx = -7

---

Concise Selina Maths Solutions, Exe-4 D Expansions (Including Substitution) ICSE Class-9th 

Question 1

If x + 2y + 3z = 0 and x³ + 4y³ + 9z³ = 18xyz ; evaluate :

………………………………

Answer

Given that x³ + 4y³ + 9z³ = 18xyz and x + 2y + 3z = 0
x + 2y = – 3z, 2y + 3z = -x and 3z + x = -2y
Now

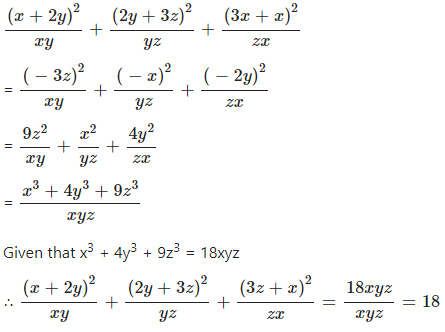
Question 2.1

If a + $\frac{\mathrm{1/}}{a}$ = m and a ≠ 0 ; find in terms of ‘m’; the value of :
$\mathrm{a\dots \dots .}$

Answer

 

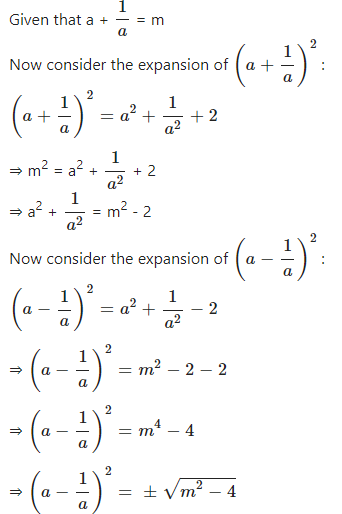
Question 2.2

If a + $\frac{\mathrm{1/}}{a}$= m and a ≠ 0 ; find in terms of ‘m’; the value of :

………………….

Answer

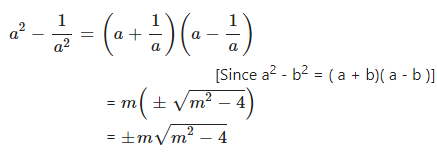
Question 3.1

In the expansion of (2x² – 8) (x – 4)²; find the value of
coefficient of x³

Answer

( 2x² – 8 )( x – 4 )²
= ( 2x² – 8 )( x² – 8x + 16 )
= 4x⁴ – 16x³ + 32x² – 8x² + 64x -128
= 4x⁴ – 16x³ + 24x² + 64x – 128
Hence,
Coefficient of x³ = -16

 

Question 3.2

Answer

( 2x² – 8 )( x – 4 )²
= ( 2x² – 8 )( x² – 8x + 16 )
= 4x⁴ – 16x³ + 32x² – 8x² + 64x -128
= 4x⁴ – 16x³ + 24x² + 64x – 128
Hence,
Coefficient of x² = 24

 

Question 3.3

Answer

( 2x² – 8 )( x – 4 )²
= ( 2x² – 8 )( x² – 8x + 16 )
= 4x⁴ – 16x³ + 32x² – 8x² + 64x -128
= 4x⁴ – 16x³ + 24x² + 64x – 128
Hence,
Constant term = -128

 

Question 4

If x > 0 and $x^{\mathrm{2\dots \dots \dots \dots ..}}$

Answer

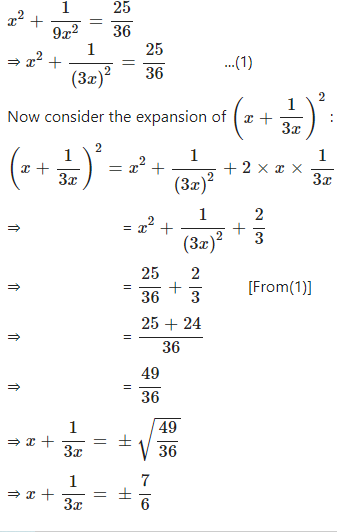
Question 5

If 2( x² + 1 ) = 5x, find :
(i) ………

(ii) ……………

Answer

 

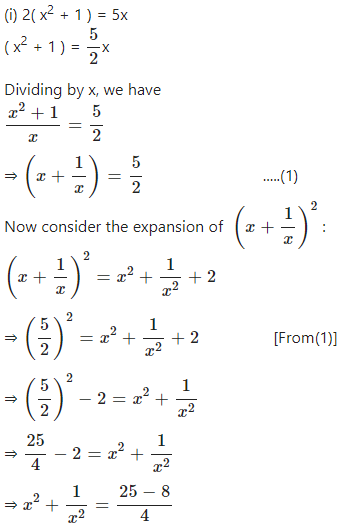
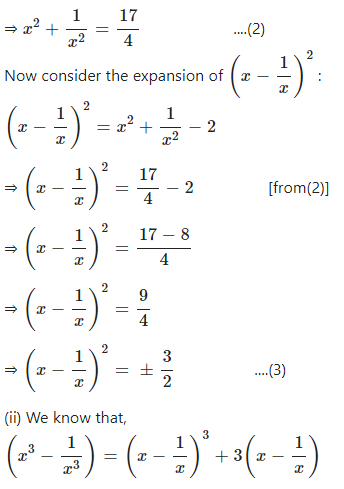
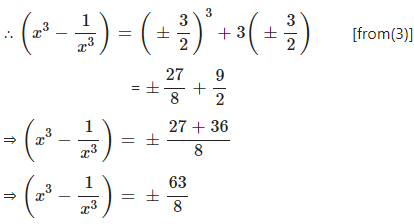
Question 6.1

Answer

a2 + b2 = 34, ab= 12

(a + b)2 = a2 + b2 + 2ab
= 34 + 2 x 12 = 34 + 24 = 58

(a – b)2 = a2 + b2 – 2ab
= 34 – 2 x 12 = 34- 24 = 10

3(a + b)2 + 5(a – b)2 = 3 x 58 + 5 x 10 = 174 + 50 = 224

 

Question 6.2

If a² + b² = 34 and ab = 12; find : 7(a – b)² – 2(a + b)²

Answer

a² + b² = 34, ab= 12

(a + b)² = a² + b² + 2ab
= 34 + 2 x 12 = 34 + 24 = 58

(a – b)² = a² + b² – 2ab
= 34 – 2 x 12 = 34- 24 = 10\

7(a – b)² – 2(a + b)²  = 7 x 10 – 2 x 58 = 70 – 116 = – 46

 

Question 7

f 3x – …………………………

Answer

 

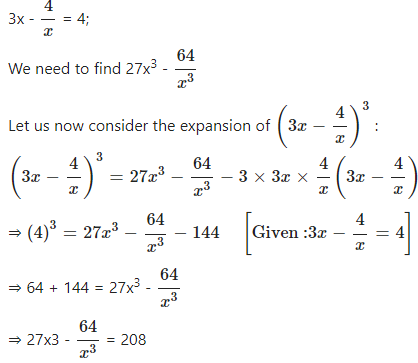
Question 8

If x² + ${\mathrm{x\dots \dots ..}}^{}$= 7 and  x ≠ 0; find the value of

……………..

Answer

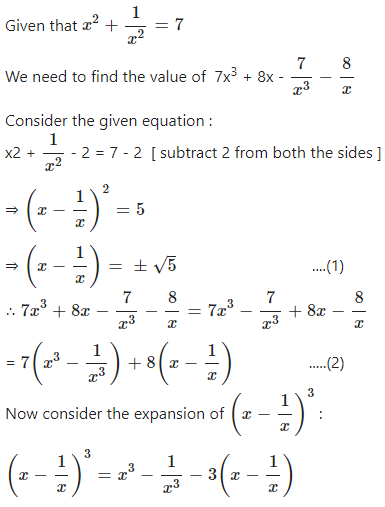
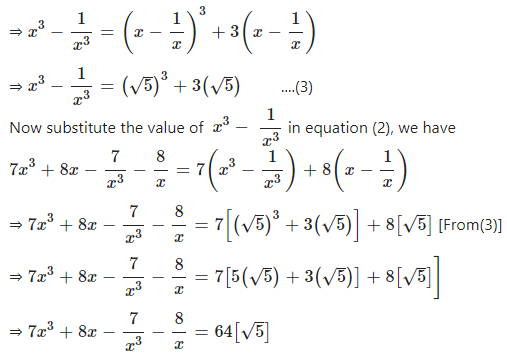
Question 9

If x =…………….. Find:…………..

Answer

 

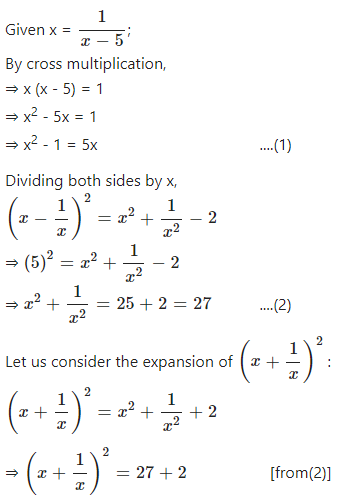
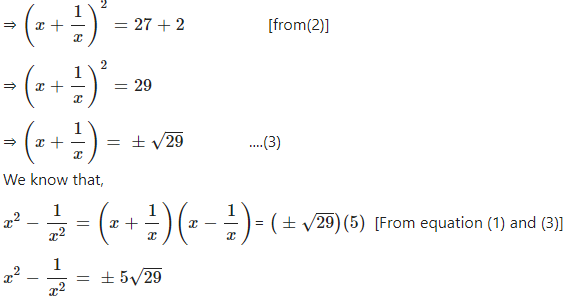
Question 10

If x = ……… find………….

Answer

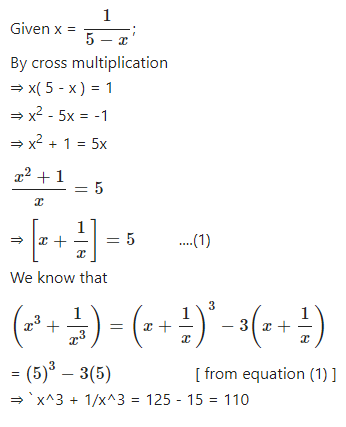
Question 11

Answer

Given that 3a + 5b + 4c = 0
3a + 5b = – 4c
Cubing both sides,
(3a + 5b)³ = (-4c)³
⇒ (3a)³ + (5b)³ + 3 x 3a x 5b (3a + 5b) = -64c³
⇒ 27a³ + 125b³ + 45ab x (-4c) = -64c³
⇒ 27a³ + 125b³ – 180abc = -64c³
⇒ 27a³ + 125b³ + 64c³ = 180abc
Hence proved.

 

Question 12

Answer

 

Question 13.1

Answer

4x² + ax + 9 = (2x + 3)²
Comparing coefficients of x terms, we get
ax = 12x
so, a = 12

 

Question 13.2

Answer

4x² + ax + 9 = (2x – 3)²
Comparing coefficients of x terms, we get
ax = -12x
so, a = -12

 

Question 13.3

Answer

9x² + (7a – 5)x + 25 = (3x + 5)²
Comparing coefficients of x terms, we get
(7a – 5)x = 30x
7a – 5 = 30
7a = 35
a = 5

 

Question 14.1

If $\frac{{\mathrm{x\dots \dots \dots \dots \dots \dots .}}^{}}{}\text{Find If}x$

Answer

 

Question 14.2

If $\frac{{\mathrm{x\dots \dots \dots \dots \dots \dots .}}^{}}{}\text{Find If}x$

Answer

 

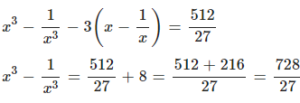
Question 15.1

The difference between two positive numbers is 4 and the difference between their cubes is 316.
Find : Their product

Answer

Given difference between two positive numbers is 4 and difference between their cubes is 316.
Let the positive numbers be a and b
a – b = 4
a³ – b³ = 316
Cubing both sides,
(a – b)³ = 64
a³ – b³ – 3ab(a – b) = 64

Given a³ – b³ = 316
So 316 – 64 = 3ab(4)
252 = 12ab
So ab = 21; product of numbers is 21

 

Question 15.2

The difference between two positive numbers is 4 and the difference between their cubes is 316.
Find : The sum of their squares

Answer

Given difference between two positive numbers is 4 and difference between their cubes is 316.
Let the positive numbers be a and b
a – b = 4                         …..(1)
a³ – b³ = 316                  …..(2)

Squaring(eq 1) both sides, we get
(a – b)² = 16
a² + b² – 2ab = 16
a² + b² = 16 + 42 = 58
Sum of their squares is 58.

---

Exercise – 4(E) Expansions (Including Substitution) ICSE Class-9th Concise Selina Mathematics

Question 1.1

Answer

Question 1.2

Simplify : ( x – 6 )( x – 4 )( x + 2 )

Answer

Using identity : (x + a)(x + b)(x + c) = x³ + (a + b + c)x² + (ab + bc + ca)x + abc

(x – 6)(x – 4)(x + 2)
= x³ + (-6 – 4 + 2)x² + [-6 × (-4) + (-4) × 2 + 2 × (-6)]x + (-6) × (-4) × 2
= x³ – 8x² + (24 – 8 – 12)x + 48
= x³ – 8x² + 4x + 48

Question 1.3

Answer

Using identity :
(x + a)(x + b)(x + c) = x³ + (a + b + c)x² + (ab + bc + ca)x + abc

( x – 6 )( x – 4 )( x – 2 )
= x³ + (-6 – 4 – 2)x² + [-6 × (-4) + (-4) × (-2) + (-2) × (-6)]x + (-6) × (-4) × (-2)
= x³ – 12x² + (24 + 8 + 12)x – 48
= x³ – 12x² + 44x – 48

 

Question 1.4

Answer

Question 2.1

Simplify using following identity : $(a\pm b)(a^2\pm ab+b^2)=a^3\pm {\mathrm{b³}}^{}$( 4x² + 6xy + 9y² )

Answer

( 2x + 3y )( 4x² + 6xy + 9y² )
= ( 2x + 3y )[ (2x)² – (2x)(3y) + (3y)² ]
= (2x)³ + (3y)³
= 8x³ + 27y³

 

Question 2.2

 Simplify using following identity : $(a\pm \mathrm{b)\dots \dots \dots \dots ..}$

Answer

 

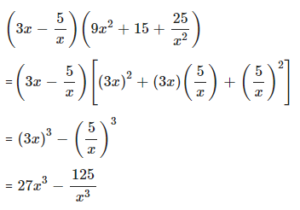
Question 2.3

Simplify using following identity : $(a\pm \mathrm{b)\dots \dots \dots \dots \dots \dots .}$

Answer

 

 

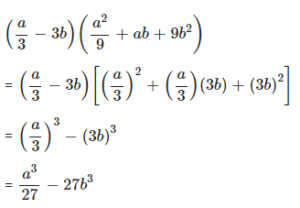
Question 3.1

Answer

Using identity: (a ± b)³ = a³ ± b³ ± 3ab(a ± b)
(104)³ = (100 + 4)³
= (100)³ + (4)³ + 3 × 100 × 4(100 + 4)
= 1000000 + 64 + 1200 × 104
= 1000000 + 64 + 124800
= 1124864

Question 3.2

Answer

(97)³ = (100 – 3)³
= (100)³ – (3)³ – 3 × 100 × 3(100 – 3)
= 1000000 – 27 – 900 × 97
= 1000000 – 27 – 87300
= 912673

Question 4

Simplify :………..

Answer

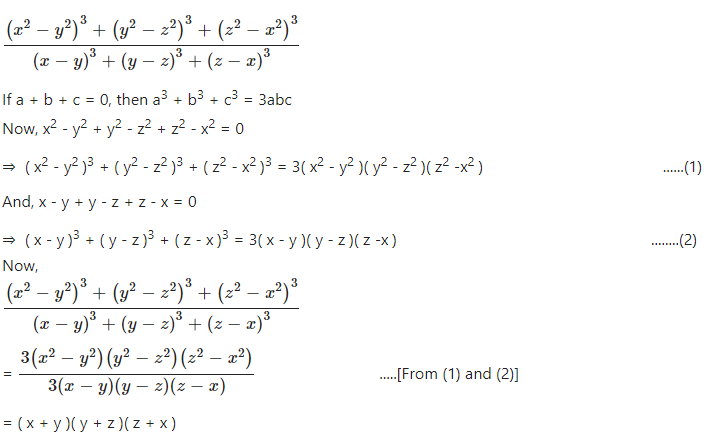
Question 5.1

Evaluate :……………

Answer

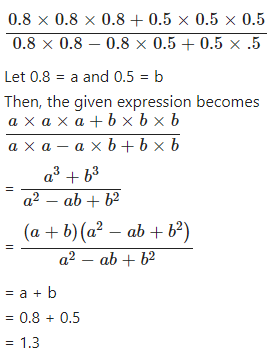
Question 5.2

Evaluate :
$\frac{\mathrm{1.2\dots \dots \dots \dots \dots \dots \dots \dots ..}}{}$

Answer

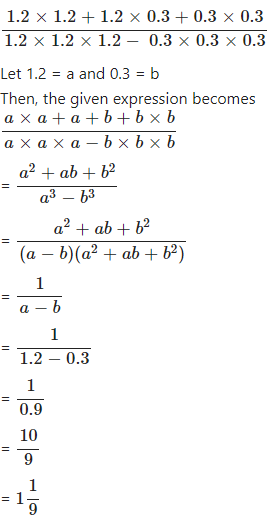
Question 6

Answer

a³ – 8b³ + 27c³ = a³ + (-2b)³ + (3c)³
Since a – 2b + 3c = 0, we have
a³ – 8b³ + 27c³ = a³ + (-2b)³ + (3c)³
= 3(a)( -2b)(3c)
= -18abc

Question 7

Answer

x + 5y = 10
⇒ (x + 5y)³ = 10³
⇒ x³ + (5y)³ + 3(x)(5y)(x + 5y) = 1000
⇒ x³ + (5y)³ + 3(x)(5y)(10) = 1000
= x³ + (5y)³ + 150xy = 1000
= x³ + (5y)³ + 150xy – 1000 = 0

Question 8

If x = 3 + 2√2, find :
(i) ……………..

(ii) …………..

(iii) …………

(iv)……${\mathrm{\dots \dots \dots \dots }}^{}$

Answer

 

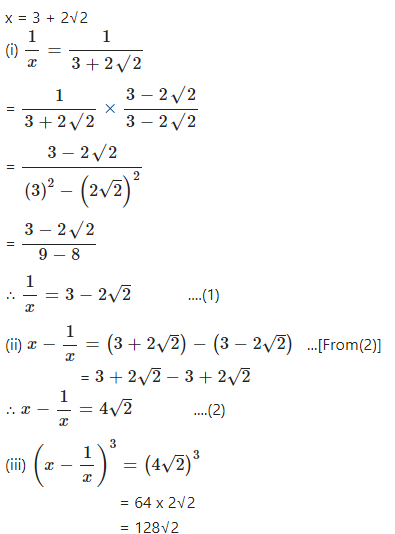
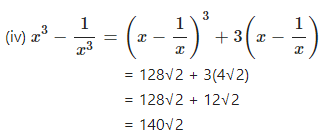
Question 9

Answer

a + b = 11 and a2 + b2 = 65
Now, (a+b)² = a² + b² + 2ab
⇒ (11)² = 65 + 2ab
⇒ 121 = 65 + 2ab
⇒  2ab = 56
⇒  ab = 28

a³ + b³ = ( a + b )( a² – ab + b2)
= (11)(65 – 28)
= 11 x 37
= 407

Question 10

Answer

Question 11.1

Answer

(a + b)(a + b) = (a + b)²
= a × a + a × b + b × a + b × b
= a² + ab + ab + b²
= a² + b² + 2ab

Question 11.2

Answer

(a + b)(a + b)(a + b)
= (a × a + a × b + b × a + b × b)(a + b)
= (a² + ab + ab + b²)(a + b)
= (a² + b² + 2ab)(a + b)
= a² × a + a² × b + b² × a + b² × b + 2ab × a + 2ab × b
= a³ + a² b + ab² + b³ + 2a²b + 2ab²
= a³ + b³ + 3a²b + 3ab²

Question 11.3

Answer

(a + b)(a + b)(a + b)
= (a × a + a × b + b × a + b × b)(a + b)
= (a² + ab + ab + b²)(a + b)
= (a² + b² + 2ab)(a + b)
= a² × a + a² × b + b² × a + b² × b + 2ab × a + 2ab × b
= a³ + a² b + ab² + b³ + 2a²b + 2ab²
= a³ + b³ + 3a²b + 3ab²

replacing b by -b, we get
= a³ + (-b)³ + 3a²(-b) + 3a(-b)²
= a³ – b³ – 3a²b + 3ab²

 

— End of Expansions ICSE Class-9th Concise Solutions :–

---

Return to – Concise Selina Maths Solutions for ICSE Class -9

---

Thanks