ML Aggarwal Fractions Exe-6.1 Class 6 ICSE Maths Solutions
ML Aggarwal Fractions Exe-6.1 Class 6 ICSE Maths Solutions. We Provide Step by Step Answer of Exe-6.1 Questions for Fractions as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-6.
ML Aggarwal Fractions Exe-6.1 Class 6 ICSE Maths Solutions
| Board | ICSE |
| Publications | Avichal Publishig Company (APC) |
| Subject | Maths |
| Class | 6th |
| Chapter-6 | Fractions |
| Writer | ML Aggarwal |
| Book Name | Understanding |
| Topics | Solution of Exe-6.1 Questions |
| Edition | 2023-2024 |
Fractions Exe-6.1
ML Aggarwal Class 6 ICSE Maths Solutions
Page-107
Question 1. Write the following division as fractions:
(i) 3 ÷ 7
(ii) 11 ÷ 78
(iii) 113 ÷ 128
Answer:
(i) 3 ÷ 7 = 3/7
(ii) 11 ÷ 78 = 11/78
(iii) 113 ÷ 128 = 113/128
Question 2. Write the following fractions in words.
(i) 2/7
(ii) 3/10
(iii) 15/28
Answer:
(i) 2/7 = Two – Seventh
(ii) 1/10 = Three – Tenth
(iii) 15/28 fifteen – Twenty eighth
Question 3. Write the following fractions in number form:
(i) one – sixth
(ii) three – eleventh,
(iii) seven-fortieth
(iv) thirteen – one hundred twenty fifth
Answer:
(i) One – sixth = 1/0
(ii) Three-eleventh = 3/11
(iiii) seven-fortieth = 7/40
(iv) Thirteen-one hundred twenty fifth = 13/125
Question 4. What fraction of each of the following is shaded part?
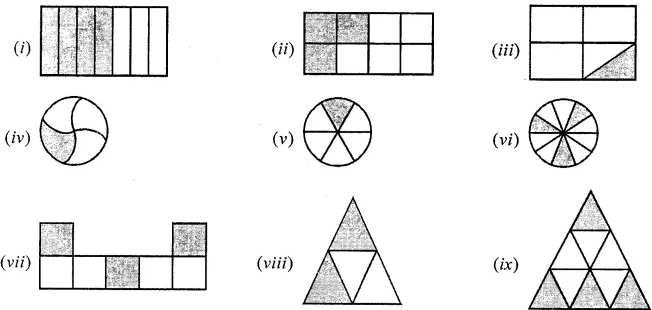
Answer:
(i) 4/7
(ii) 3/8
(iii) 1/8
(iv) 1/4
(v) 1/6
(vi) 3/10
(vii) 3/7
(viii) 2/4
(ix) 4/9
Question 5. Shade the parts of the following figures according to given fractions:
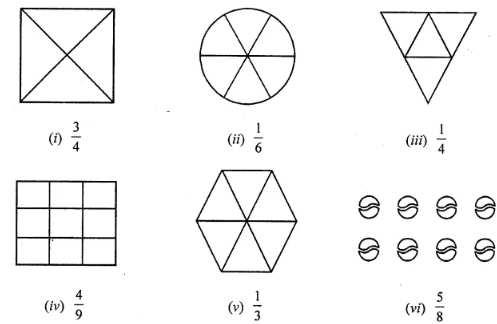
Answer:
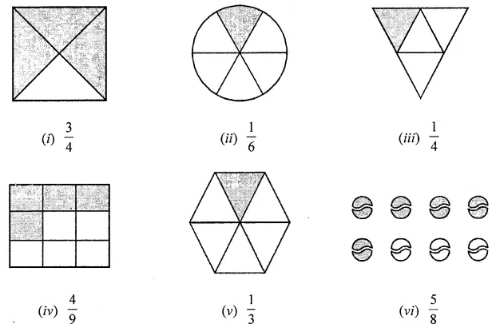
Fractions Exe-6.1
ML Aggarwal Class 6 ICSE Maths Solutions
Page-108
Question 6. Write the fraction in which
(i) numerator = 5 and denominator = 13
(ii) denominator = 23 and numerator = 17
Answer:
(i) 5/13
(ii) 17/23
Question 7. Shabana has to stitch 35 dresses. So, ar she has stitched 21 dresses. What fraction of dresses has she stitched?
Answer:
Number of dresses she had to stiches = 35
Number of dresses she has finished = 21
∴ Fraction of dresses she has finished = 21/35 = 3/5
Question 8. What fraction of a day is 8 hours ?
Answer:
Number of hours in a day = 24 hours
∴ Required fraction = 8/24
Question 9. What fraction of an hour is 45 minutes ?
Answer:
An hour (1 hour) = 60 minutes
∴ Required fraction = 45/60
Question 10. How many natural numbers are there from 87 to 97? What fraction of them are prime numbers?
Answer:
The natural numbers from 87 to 97 are 87, 88, 89, 90, 91, 92, 93, 94, 95, 96 and 97. Total number of natural number = 11 Out of these, the prime numbers are 87 and 97
Total number of these prime numbers = 2
∴ Required fraction = 2/11
— : End of ML Aggarwal Fractions Exe-6.1 Class 6 ICSE Maths Solutions :–
Return to – ML Aggarwal Maths Solutions for ICSE Class -6
Thanks
