Framing Algebraic Expressions ICSE Class-6th Concise Mathematics Selina Solutions Chapter-21 (Including Evaluation). We provide step by step Solutions of Exercise / lesson-21 Framing Algebraic Expressions (Including Evaluation) for ICSE Class-6 Concise Selina Mathematics. Our Solutions contain all type Questions to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-6 .
Framing Algebraic Expressions ICSE Class-6th Concise Mathematics Selina Solutions Chapter-21 (Including Evaluation)
Exercise – 21
Framing Algebraic Expressions ICSE Class-6th
Concise Mathematics Selina Solutions Chapter-21 (Including Evaluation)
Question- 1.
Write in the form of an algebraic expression :
(i) Perimeter (P) of a rectangle is two times the sum of its length (l) and its breadth (b).
(ii) Perimeter (P) of a square is four times its side.
(iii) Area of a square is square of its side.
(iv) Surface area of a cube is six times the square of its edge.
Answer-1
(i) Let P be the perimeter and / be the length, and b be the breadth.
P = 2 (l + b)
(ii) Let P be the perimeter and a be the side of the square.
P = 4a
(iii) Let A be the area of the square and a be the sides of the square.
A = (a)2
(iv) Let S be the surface area and a be the edges of the cube.
S = 6a2
Question -2.
Express each of the following as an algebraic expression :
(i) The sum of x and y minus m.
(ii) The product of x and y divided by m.
(iii) The subtraction of 5m from 3n and then adding 9p to it.
(iv) The product of 12, x, y and z minus the product of 5, m and n.
Answer-2
i) x + y – m
(ii) xy⁄m
(iii) 3n – 5m + 9p
(iv) 12xyz – 5mn
(v) p + 2r – s – (a + 3n + 4x)
Question -3.
Construct a formula for the following :
Total wages (₹ W) of a man whose basic wage is (₹ B) for t hours week plus (₹ R) per hour, if he Works a total of T hours.
Answer-3
Wages for t hours = ₹ B
Wages for overtime = R(T – t)
=> Total wages = Wages for t hours + wages for overtime of (T – t) hours
=> ₹ W = ₹ B + ₹ R (T – t)
Question- 4.
If x = 4, evaluate :
(i) 3x + 8
(ii) x2 – 2x
(iii) x²⁄m
Answer-4
(i) 3x + 8
= (3 × 4) + 8
= 12 + 8
= 20
(ii) x2 – 2x
= (4)2 − 2(4)
= (4 × 4) − (2 × 4)
= 16 − 8
= 8
(iii) x²⁄m
= 4²⁄2
= 4 x 4⁄2
= 16⁄2
= 8
Question 5.
(i) 5m – 6
(ii) 2m2 + 3m
(iii) (2m)2
Answer -5
(i) 5m − 6
= (5 × 6) − 6
= 36 − 6
= 30
(ii) 2m2 + 3m
= 2 (6)2 + 3 (6)
= 2 × 6 × 6 + 3 × 6
= 72 + 18
= 90
(iii) (2m)2
= (2 × m) × (2 × m)
= (2 × 6) × (2 × 6)
= 12 × 12
= 144
Question -6.
(i) 12x + 7
(ii) 5x2 + 4x
(iii) x²⁄8
Answer-6
(i) 12x + 7
= (12 × 4) + 7
= 48 + 7
= 55
(ii) 5x2 + 4x
= (5 × 4 × 4) + 4 (4)
= 80 + 16
= 96
(iii) x²⁄8
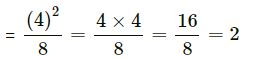
Question- 7.
If m = 2, evaluate :
(i) 16m – 7
(ii) 15m2 – 10m
(iii) …1⁄4..m³………
Answer-7
(i) 16m – 7
= (16 × 2) – 7
= 32 – 7
= 25
(ii) 15m2 – 10m
= 15 (2)2 − 10(2)
= (15 × 2 × 2) − (10 × 2)
= 60 − 20
= 40
(iii) …1⁄4..m³………
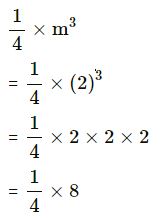
= 2
Question- 8.
If x = 10, evaluate :
(i) 100x + 225
(ii) 6x2 – 25x
(iii) 1⁄50..x³.
Answer-8
If x = 10, evaluate :
(i) 100x + 25
= (100 × 10) + 225
= 1000 + 225
= 1225
(ii) 6x2 – 25x
= 6(10)2 − 25(10)
= (6 × 10 × 10) − (25 × 10)
= 600 − 250
= 350

Question-9
(i) 5a
(ii) a2
(iii) a3
Answer- 9.
If a = – 10, evaluate :
(i) 5a
= 5 × (− 10)
= − 50
(ii) a2
= (− 10)2
= − 10 × (− 10)
= 100
(iii) a3
= a × a × a
= (− 10)3
= (− 10) × (− 10) × (− 10)
= − 1000
Question -10.
If x = – 6, evaluate :
(i) 11x
(ii) 4x2
(iii) 2x3
Answer-10
(i) 11x
= 11 × (− 6)
= − 66
(ii) 4x2
= 4 × (− 6) × (− 6)
= 4 × 36
= 144
= 2 × (− 6) × (− 6) × (− 6)
= 2 × (− 216)
= − 432
Question -11.
If m = – 7, evaluate :
(i) 12m
(ii) 2m2
(iii) 2m3
Answer-11
(i) 12m
= 12 × (− 7)
= − 84
(ii) 2m2
= 2 × m × m
= 2 × (− 7) × (− 7)
= 2 × 49
= 98
= 2 × (− 7) × (− 7) × (− 7)
= 2 × (− 343)
= − 686
Question -12.
Find the average (A) of four quantities p, q, r and s. If A = 6, p = 3, q = 5 and r = 7 ; find the value of s.
Answer-12
Given, average of four quantities (A) = 6
and p = 3, q = 5, r = 7 and s = ?
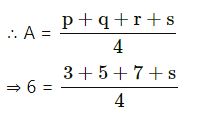
⇒ 6 × 4 = 15 + s
⇒ s = 24 − 15
⇒ s = 9
Question -13.
If a = 5 and b = 6, evaluate :
(i) 3ab
(ii) 6a2b
(iii) 2b2
Answer-13
(i) 3ab
= 3 × a × b
= 3 × 5 × 6
= 90
(ii) 6a2b
= 6 × a × a × b
= 6 × 5 × 5 × 6
= 900
(iii) 2b2
= 2 × b × b
= 2 × 6 × 6
= 72
Question -14.
If x = 8 and y = 2, evaluate :
(i) 9xy
(ii) 5x2y
(iii) (4y)2
Answer-14:
(i) 9xy
= 9 × x × y
= 9 × 8 × 2
= 144
(ii) 5x2y
= 5 × x × x × y
= 5 × 8 × 8 × 2
= 640
(iii) (4y)2
= 4 × y × 4 × y
= 4 × 2 × 4 × 2
= 8 × 8
= 64
Question- 15.
If x = 5 and y = 4, evaluate :
(i) 8xy
(ii) 3x2y
(iii) 3y2
Answer-15:
(i) 8xy
= 8 × x × y
= 8 × 5 × 4
= 160
(ii) 3x2y
= 3 × x × x × y
= 3 × 5 × 5 × 4
= 300
(iii) 3y2
= 3 × y × y
= 3 × 4 × 4
= 48
Question- 16.
If y = 5 and z = 2, evaluate :
(i) 100yz
(ii) 9y2z
(iii) 5y2
(iv) (5z)3
Answer-16:
(i) 100yz
= 100 × y × z
= 100 × 5 × 2
= 1000
(ii) 9y2z
= 9 × y × y × z
= 9 × 5 × 5 × 2
= 450
(iii) 5y2
= 5 × y × y
= 5 × 5 × 5
= 125
(iv) (5z)3
= (5 × z) × (5 × z) × (5 × z)
= 5 × 2 × 5 × 2 × 5 × 2
= 10 × 10 × 10
= 1000
Question -17.
If x = 2 and y = 10, evaluate :
(i) 30xy
(ii) 50xy2
(iii) (10x)2
(iv) 5y2
Answer-17:
(i) 30xy
= 30 × x × y
= 30 × 2 × 10
= 600
(ii) 50xy2
= 50 × x × y × y
= 50 × 2 × 10 × 10
= 10000
(iii) (10x)2
= (10 × x) × (10 × x)
= 10 × 2 × 10 × 2
= 400
(iv) 5y2
= 5 × y × y
= 5 × 10 × 10
= 500
Question -18.
If m = 3 and n = 7, evaluate :
(i) 12mn
(ii) 5mn2
(iii) (10m)2
(iv) 4n2
Answer-18
(i) 12mn
= 12 × m × n
= 12 × 3 × 7
= 252
(ii) 5mn2
= 5 × m × n × n
= 5 × 3 × 7 × 7
= 735
(iii) (10m)2
= (10 × m) × (10 × m)
= (10 × 3) × (10 × 3)
= 30 × 30
= 900
(iv) 4n2
= 4 × n × n
= 4 × 7 × 7
= 196
Question -19.
If a = -10, evaluate :
(i) 3a – 2
(ii) a2 + 8a
(iii) ….1⁄5..a².……
Answer-19:
(i) 3a – 2
= (3 × a) − 2
= 3 × (− 10) − 2
= − 30 − 2
= − 32
(ii) a2 + 8a
= (a × a) + (8 × a)
= (− 10 × (− 10)) + (8 × (− 10))
= 100 + (− 80)
= 100 − 80
= 20
(iii)
. …..
…..
= 20
Question -20.
If x = -6, evaluate :
(i) 4x – 9
(ii) 3x2 + 8x
(iii) …x²⁄2..…..
Answer-20:
(i) 4x – 9
= (4 × x) – 9
= (4 × (– 6)) – 9
= – 24 – 9
= – 33
(ii) 3x2 + 8x
= (3 × x × x) + (8 × x)
= (3 × (− 6) × (− 6)) + (8 × (− 6))
= − 108 + (− 48)
= 60
(iii)
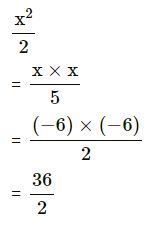
= 18
Question -21.
If m = -8, evaluate :
(i) 2m + 21
(ii) m2 + 9m
(iii) m²⁄4..
Answer-21:
(i) 2m + 21
= 2 × m + 21
= 2 × (− 8) + 21
= − 16 + 21
= 5
(ii) m2 + 9m
= (m × m) + (9 × m)
= (− 8 × − 8) + (9 × (− 8))
= 64 + (− 72)
= 64 − 72
= − 8
(iii)
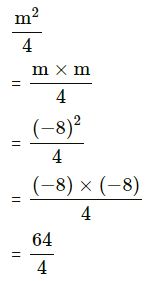
= 16
Question- 22.
If p = -10, evaluate :
(i) 6p + 50
(ii) 3p2 – 20p
(iii) p²⁄50..
Answer-22:
(i) 6p + 50
= (6 × p) + 50
= (6 × (− 10)) + 50
= − 60 + 50
= − 10
(ii) 3p2 – 20p
= (3 × p × p) − (20 × p)
= (3 × (− 10) × (− 10)) − (20 × (− 10))
= 300 − (− 200)
= 300 + 200
= 500
(iii)
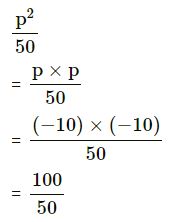
= 2
Question- 23.
If y = -8, evaluate :
(i) 6y + 53
(ii) y2 + 12y
(iii) y³⁄4..
Answer23:
(i) 6y + 53
= (6 × y) + 53
= (6 × (− 8)) + 53
= − 48 + 53
= 5
(ii) y2 + 12y
= (y × y) + (12 × y)
= ((− 8) × (− 8)) + (12 × (− 8))
= 64 + (− 96)
= −32
(iii)

Question -24.
If x = 2 and 7 = -4, evaluate :
(i) 11xy
(ii) 5x2y
(iii) (5y)2
(iv) 8x2
Answer-24:
(i) 11xy
= 11 × x × y
= 11 × 2 × (− 4)
= − 88
(ii) 5x2y
= 5 × x × x × y
= 5 × 2 × 2 × (− 4)
= − 80
(iii) (5y)2
= 5 × y × 5 × y
= 5 × (− 4) × 5 × (− 4)
= (− 20) × (− 20)
= 400
(iv) 8x2
= 8 × x × x
= 8 × 2 × 2
= 32
If m = 9 and n = -2, evaluate
(i) 4mn
(ii) 2m2n
(iii) (2n)3
Answer-25:
(i) 4mn
= 4 × m × n
= 4 × 9 × (− 2)
= − 72
(ii) 2m2n
= 2 × m × m × n
= 2 × 9 × 9 × (− 2)
= 2 × 81 × (− 2)
= − 324
(iii) (2n)3
= (2 × n) × (2 × n) × (2 × n)
= (2 × (− 2)) × (2 × (− 2)) × (2 × (− 2))
= (− 4) × (− 4) × (− 4)
= − 64
Question- 26.
If m = -8 and n = -2, evaluate :
(i) 12mn
(ii) 3m2n
(iii) (4n)2
Answer-26:
(i) 12mn
= 12 × m × n
= 12 × (− 8) × (− 2)
= 192
(ii) 3m2n
= 3 × m × m × n
= 3 × 64 × (− 2)
= − 384
(iii) (4n)2
= 4 × n × 4 × n
= (4 × (− 2)) × (4 × (− 2))
= (− 8) × (− 8)
= 64
Question -27.
If x = -5 and y = -8, evaluate :
(i) 4xy
(ii) 2xy2
(iii) 4x2
(iv) 3y2
Answer-27:
(i) 4xy
= 4 × x × y
= 4 × (− 5) × (− 8)
= 160
(ii) 2xy2
= 2 × x × y × y
= 2 × (− 5) × (− 8) × (− 8)
= − 10 × 64
= − 640
(iii) 4x2
= 4 × x × x
= 4 × (− 5) × (− 5)
= 100
(iv) 3y2
= 3 × y × y
= 3 × (− 8) × (− 8)
= 192
Question -28.
Find T, if T = 2a – b, a = 7 and b = 3.
Answer-28:
T = 2a – b, a = 1 and b = 3
Put the value of a = 1, and b = 3 in above equation
T = (2 × 7) − 3
T = 14 – 3
T = 11
Question- 29.
From the formula B = 2a2 – b2, calculate the value of B when a = 3 and b = -1.
Answer-29:
B = 2a2 – b2
Put the values of a = 3 and b = − 1 in above equation
B = 2 × (3)2 – (− 1)2
B = 18 – 1
B = 17
Value of B is = 17
Question- 30.
The wages ₹ W of a man earning ₹ x per hour for t hours are given by the formula W = xt. Find his wages for working 40 hours at a rate of ₹ 39.45 per hour.
Answer-30:
T = 40 hours
x = ₹ 39.45
W = xt = 40 × 39.45
W = ₹ 1578
Question -31.
The temperature in Fahrenheit scale is represented by F and the tempera¬ture in Celsius scale is represented by C. If F = 9⁄5 x C + 32, find F when C = 40.
Answer-31:
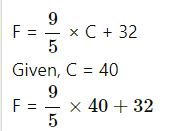
= 9 × 8 + 32
F = 104°
End of Framing Algebraic Expressions Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -6
Thanks


