Friction Numerical Motion on Inclined Plane Class 11 Nootan ISC Physics Solutions Ch-7. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-11 Physics.
Friction Numerical Motion on Inclined Plane Class 11 Nootan ISC Physics Solutions
| Board | ISC |
| Class | 11 |
| Subject | Physics |
| Writer | Kumar and Mittal |
| Publication | Nageen Prakashan |
| Chapter-7 | Friction |
| Topics | Numerical Motion on Inclined Plane |
| Academic Session | 2024-2025 |
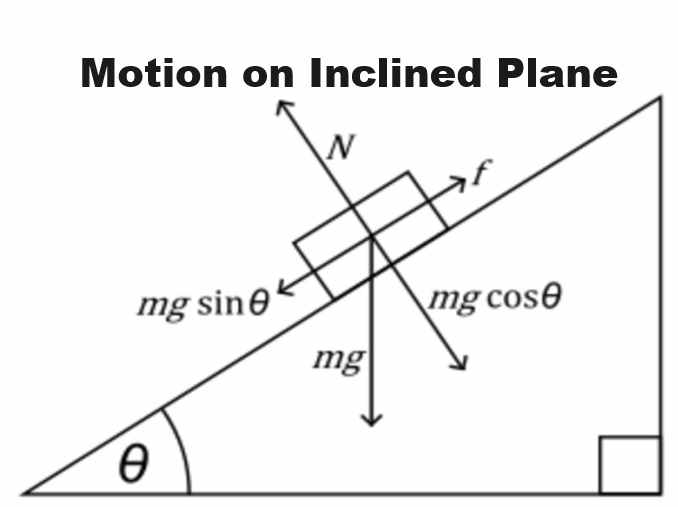
Numerical Motion on Inclined Plane
Friction Numerical Class 11 ISC Nootan Solutions Ch-7 of Kumar and Mittal Physics of Nageen Prakashan
Question-7: A block placed on a rough inclined plane of length 4.0 m just begins to slide down when the upper end of the plane is 1.0 m high from the ground. Calculate the coefficient of static friction.
Answer-
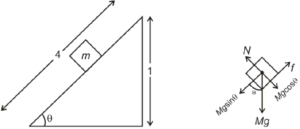
N = mg cosθ
mg sinθ = μmg cosθ
μ = tanθ
μ = 1/√4² – 1² = 1 /√15 = 0.258
Question-8: A block rests on a plane of variable inclination. Find the incline of the plane with the horizontal at which the block just slides down. The coefficient of friction between the block and the plane is µs = 1/√3.
Answer- N = mg cosθ
mg sinθ = μN
mg sinθ = μmg cosθ
μ = tanθ
θ = tan^-1(μ) = tan^-1 (1/√3) = 30°
Question-9: A block of mass 0.05 kg when placed on a rough 15°-inclined plane slides down without acceleration. The inclination is then increased to 30°. What would be the acceleration of the block? g = 9.8 m/s²
Answer- When the block of mass m = 0.05 kg is placed on 15° incline, its acceleration is zero. if f is the force of friction
f=mg sin 15°
when put on 30° incline let acceleration be a
so, mg sin 30° – f =ma or mg sin 30° – mg sin° =ma
a=g(sin 30° – sin 15°) = 9.8 m/s²(0.5 – 0.258)
a ≈ 2.63 m/s²
Question-10: A body is in limiting equilibrium on a rough plane inclined at 30° with the horizontal. When the inclination is increased to 45°, the body slides down with acceleration. Find this acceleration. Take g = 9.8 m/s².
Answer- in limiting equilibrium , fs = mg sinθ
μs x mg cos θ = mg sin θ
μs = (1/√3)
mg sin θ – μ x mg cos θ =ma
g x sin θ – 1/√3 x g x cos 45° =a
a = g x (1/√2 – 1√3 x 1/√2)
a= 7.154 / 56
a = 2.93 m/s²
Question-11: A body slides down from rest from the top of a 6.4 m long rough plane inclined at 30° with the horizontal. Find the time taken by the block in reaching the bottom of the plane. Take µk = 0.2 and g = 9.8 m/s².
Answer- acceleration of block due to gravity on the plane is given by;
a = g SinΘ – f / m
a = g SinΘ – µR Cosθ / m
a = g SinΘ – µmg Cosθ / m
a = 9.8 x Sin 30 – µg Cosθ
a = 4.9 – (0.2)(9.8) Cos (30)
a = 4.9 – 1.697 = 3.20 m/s²
t = ?
If S = 6.4m
S = u t + 1/2at² ……………. u = initial velocity = 0 at the top of inclined plane
6.4 = 0 + 1/2(3.2)t²
6.4 = 1.6t²
=> t² = 6.4 / 1.6
=> t²= 4
=> t = 2 s
—: end of Friction Numerical Motion on Inclined Plane Class 11 Nootan ISC Solutions Ch-7 :—
Return to : – Nootan Solutions for ISC Physics Class-11 Nageen Prakashan
Thanks
Please Share with your friends if helpful