Fundamental Concepts ICSE Class-7 Concise Selina mathematics Solutions Chapter-11. We provide step by step Solutions of Exercise / lesson-11 Fundamental Concepts ( Including Fundamental Operations ) for ICSE Class-7 Concise Selina Mathematics. Our Solutions contain all type Questions with Exe-11 A , Exe-11 B Exe-11 C , Exe-11 D , Exe-11 E and Exe-11 F to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-7.
Fundamental Concepts ICSE Class-7 Concise Selina mathematics Solutions Chapter-11
–: Select Topics :–
Exercise – 11 A Fundamental Concepts ICSE Class-7 mathematics
Question 1.
Separate constant terms and variable terms from tile following :

Answer
Constant is only 8 other are variables.
Question 2.
Constant is only 8 others are variables
(i) 2x ÷ 15
(ii) ax+ 9
(iii) 3x2 × 5x
(iv) 5 + 2a-3b
(v) 2y – z÷x
(vi) 3p x q ÷ z
(vii) 12z ÷ 5x + 4
(viii) 12 – 5z – 4
(ix) a3 – 3ab2 x c
Answer
(i)
2x ÷ 15 = 2x/15
It is a monomial as it has one term.
(ii)
ax + 9: It is binomial
(∵ It has two terms)
(iii)
3x2 × 5x = 15x3 – It is monomial
(∵ It has one term)
(iv)
5 + 2a – 3b – It is trinomial
(∵ It has three terms)
(v)
2y –(7/3) z ÷ x = 2y – (7z/3x) – It is binomial
(∵ It has two terms)
(vi)
3p x q ÷ z – (3pq/z) – It is monomial
(∵ It has one terms)
(vii)
12z ÷ 5x + 4 = (12z/5x)+4 – It is binomial
(∵ It has two terms)
(viii)
12 – 5 z – 4 = 8 – 5 z – It is binomial
(∵ It has two terms)
(ix)
a3 – 3ab2 x c = a3 – 3ab2c – It is binomial
(∵ It has two terms)
Question 3.
Write the coefficient of:
(i) xy in – 3axy
(ii) z2 in p2yz2
(iii) mn in -mn
(iv) 15 in – 15p2
Answer
(i) Co-efficient of xy in – 3 axy = – 3a
(ii) Co-efficient of z2 in p2yz2 = p2y
(iii) Co-efficient of mn in – mn = – 1
(iv) Co-efficient of 15 in – 15p2 is -p2
Question 4.
For each of the following monomials, write its degree :
(i) 7y
(ii) – x2y
(iii) xy2z
(iv) – 9y2z3
(v) 3 m3n4
(vi) – 2p2q3r4
Answer
(i) Degree of 7y = 1
(ii) Degree of – x2y = 2 + 1 = 3
(iii) Degree of xy2z = 1 + 2 + 1 = 4
(iv) Degree of – 9y2z3 = 2 + 3 = 5
(v) Degree of 3m3n4 = 3 + 4 = 7
(vi) Degree of – 2p2q3r4 = 2 + 3 + 4 = 9
Question 5.
Write the degree of each of the following polynomials :
(i) 3y3-x2y2 + 4x
(ii) p3q2 – 6p2q5 + p4q4
(iii) – 8mn6+ 5m3n
(iv) 7 – 3x2y + y2
(v) 3x – 15
(vi) 2y2z + 9yz3
Answer
(i) The degree of 3y3 – x2y2+ 4x is 4 as x2
(ii) The degree of p3q2 – 6p2q5 – p4q4 is 8 as p4 q4 is the term which has highest degree.
(iii) The degree of – 8mn6 + 5m3n is 7 as – 8mx6 is the term that has the highest degree.
(iv) The degree of 7 – 3x2y + y2 is 3 as – 3x2y is the term which has the highest degree.
(v) The degree of 3x – 15 is 1 as 3x is the term which is highest degree.
(vi) The degree of 2y2z + 9yz3 is 4 as 9yz3 has the highest degree.
Question 6.
Group the like term together :
(i) 9x2, xy, – 3x2, x2 and – 2xy
(ii) ab, – a2b, – 3ab, 5a2b and – 8a2b
(iii) 7p, 8pq, – 5pq – 2p and 3p
Answer
(i) 9x2, – 3x2 and x2 are like terms xy and – 2xy are like terms.
(ii)
ab, – 3ab, are like terms,
– a2b, 5a2b, – 8a2b are like terms
(iii)
7p, – 2p and 3p are like terms,
8pq, – 5pq are like terms.
Question 7.
Write numerical co-efficient of each of the followings :
(i) y
(ii) -y
(iii) 2x2y
(iv) – 8xy3
(v) 3py2
(vi) – 9a2b3
Answer
(i) Co-efficient of y = 1
(ii) Co-efficient of-y = – 1
(iii) Co-efficient of 2x2y is = 2
(iv) Co-efficient of – 8xy3 is = – 8
(v) Co-efficient of 3py2 is = 3
(vi) Co-efficient of – 9a2b3 is = – 9
Question 8.
In -5x3y2z4; write the coefficient of:
(i) z2
(ii) y2
(iii) yz2
(iv) x3y
(v) -xy2
(vi) -5xy2z
Also, write the degree of the given algebraic expression.
Answer
(i)
-5x3y2z4
Co-efficient of z2 is -5x3y2z2
Degree of the given expression is 3 + 2 + 4 = 9
(ii)
-5x3y2z4
Co-efficient of y2 is -5x3z4
Degree of the given expression is 3 + 2 + 4 = 9
(iii)
-5x3y2z4
Co-efficient of yz2 is -5x3yz2
Degree of the given expression is 3 + 2 + 4 = 9
(iv)
-5x3y2z4
Co-efficient of x3y is -5yz4
Degree of the given expression is 3 + 2 + 4 = 9
(v)
-5x3y2z4
Co-efficient of -xy2 is 5x2z4
Degree of the given expression is 3 + 2 + 4 = 9
(vi)
-5x3y2z4
Co-efficient of -5xy2z is x2z3
Degree of the given expression is 3 + 2 + 4 = 9
Fundamental Concepts ICSE Class-7 Exe-11 B
Question 1.
Fill in the blanks :
(i) 8x + 5x = ………
(ii) 8x – 5x =……..
(iii) 6xy2 + 9xy2 =……..
(iv) 6xy2 – 9xy2 = ………
(v) The sum of 8a, 6a and 5b = ……..
(vi) The addition of 5, 7xy, 6 and 3xy = …………
(vii) 4a + 3b – 7a + 4b = ……….
(viii) – 15x + 13x + 8 = ………
(ix) 6x2y + 13xy2 – 4x2y + 2xy2 = ……..
(x) 16x2 – 9x2 = and 25xy2 – 17xy2=………
Answer
(i) 8x + 5x = 13x
(ii) 8x – 5x = 3x
(iii) 6xy2 + 9xy2 = 15xy2
(iv) 6xy2 – 9xy2 = -3xy2
(v)
The sum of 8a, 6a and 5b
= 8a + 6a + 5b = 14a + 5b
(vi)
The addition of 5, 7xy, 6 and 3xy
= 5 + 6 + 7xy + 3xy = 11 + 10 xy
(vii)
4a + 3b – 7a + 4b
= 4a – 7a + 3b + 4b = -3a + 7b = 7b – 3a
(viii) – 15x + 13x + 8 = – 2x + 8 = 8 – 2x
(ix)
6x2y + 13xy2 – 4x2y + 2xy2
= 6x2y – 4x2y + 13xy2 + 2xy2 = 2x2y + 15xy2
(x) 16x2 – 9x2 = 7x2 and 25xy2 – 17xy2 = 8xy2
Question 2.
Add :
(i)- 9x, 3x and 4x
(ii) 23y2, 8y2 and – 12y2
(iii) 18pq – 15pq and 3pq
Answer
(i)
– 9x, 3x and 4x
= – 9x + 7x = – 2x
(ii)
23y2 , 8y2 and – 12y2
= 31y2 – 12y2 = 19y2
(iii)
18pq – 15pq and 3pq
= 18pq + 3pq – 15pq = 21pq – 15pq = 6 pq
Question 3.
Simplify :
(i) 3m + 12m – 5m
(ii) 7n2 – 9n2 + 3n2
(iii) 25zy—8zy—6zy
(iv) -5ax2 + 7ax2 – 12ax2
(v) – 16am + 4mx + 4am – 15mx + 5am
Answer
(i)
3m + 12m – 5m
= 15m – 5m = 10m
(ii)
7n2 – 9n2 + 3n2
= 7n2 + 3n2 – 9n2
= 10n2 – 9n2 = n2
(iii)
25zy – 8zy – 6zy
= 25zy – 14zy = 11zy
(iv)
-5ax2 + 7ax2 – 12ax2
= – 5ax2 – 12ax2 + 7ax2
= – 17ax2 + 7ax2 = – 10ax2
(v)
– 16am + 4mx + 4am – 15mx + 5am
= – 16am + 4am + 5am + 4mx – 15mx
= – 16am + 9am + 4mx – 15mx
= – 7 am – 11 mx
Question 4.
Add :
(i) a + i and 2a + 3b
(ii) 2x + y and 3x – 4y
(iii)- 3a + 2b and 3a + b
(iv) 4 + x, 5 – 2x and 6x
Answer
(i)
a + b and 2a + 3b
= a + b + 2a + 3b
= a + 2a + b + 3b = 3a + 4b
(ii)
2x + y and 3x – 4y
= 2x + 3x + y – 4y
= 5x – 3y
(iii)
– 3a + 2b and 3a + b
= – 3a + 3a + 2b + b
= 0 + 3b = 3b
(iv)
4 + x, 5 – 2x and 6x
= x – 2x + 6x + 4 + 5
= 7x – 2x + 9
= 5x + 9
Question 5.
Find the sum of:
(i) 3x + 8y + 7z, 6y + 4z- 2x and 3y – 4x + 6z
(ii) 3a + 5b + 2c, 2a + 3b-c and a + b + c.
(iii) 4x2+ 8xy – 2y2 and 8xy – 5y2 + x2
(iv) 9x2 – 6x + 7, 5 – 4x and 6 – 3x2
(v) 5x2 – 2xy + 3y2 and – 2x2 + 5xy + 9y2
and 3x2 -xy- 4y2
(vi) a2 + b2 + 2ab, 2b2 + c2 + 2bc
and 4c2-a2 + 2ac
(vii) 9ax – 6bx + 8, 4ax + 8bx – 7
and – 6ax – 46x – 3
(viii) abc + 2 ba + 3 ac, 4ca – 4ab + 2 bca
and 2ab – 3abc – 6ac
(ix) 4a2 + 5b2 – 6ab, 3ab, 6a2 – 2b2
and 4b2 – 5 ab
(x) x2 + x – 2, 2x – 3x2 + 5 and 2x2 – 5x + 7
(xi) 4x3 + 2x2 – x + 1, 2x3 – 5x2– 3x + 6, x2 + 8 and 5x3 – 7x
Answer
(i)
3x + 8y + 7z; 6y + 4z- 2x and 3y – 4x + 6z
3x + 8y + 7z + 6y + 4z – 2x + 3y – 4x + 6z
= 3x – 6x + 17y + 17z
= – 3x + 17y + 17z
(ii)
3a + 5b + 2c, 2a + 3b-c and a + b + c.
3a + 5b + 2c + 2a + 3b – c + a + b + c.
= 6a + 9b + 3c – c
= 6a + 9b + 2c
(iii)
4x2+ 8xy – 2y2 and 8xy – 5y2 + x2
4x2+ 8xy – 2y2 + 8xy – 5y2 + x2
= 4x2 + x2 + 8xy + 8xy – 2y2 – 5y2
= 5x2 + 16xy – 7y2
(iv)
9x2 – 6x + 7, 5 – 4x and 6 – 3x2
9x2 – 6x + 7 + 5 – 4x + 6 – 3x2
= 9x2 – 3x2 – 6x – 4x + 7 + 5 + 6
= 6x2 – 10x + 18
(v)
5x2 – 2xy + 3y2 and – 2x2 + 5xy + 9y2 and 3x2 -xy- 4y2
5x2 – 2xy + 3y2 + – 2x2 + 5xy + 9y2 + 3x2 -xy- 4y2
= 5x2 – 2x2 + 3x2 – 2xy + 5xy – xy + 3y2 + 9y2 – 4y2
= 8x2 – 2x2 + 5xy – 3xy + 12y2 – 4y2
=6x2 + 2xy + 8y2
(vi)
a2 + b2 + 2ab, 2b2 + c2 + 2bc and 4c2 -a2 + 2ac
a2 + b2 + 2ab + 2b2 + c2 + 2bc + 4c2 -a2 + 2ac
= a2 – a2 + b2 + 2b2 + c2 + 4c2 + 2ab + 2bc + 2ac
= 3b2 + 5c2 + 2ab + 2bc + 2ac
(vii)
9ax – 6bx + 8, 4ax + 8bx – 7 and – 6ax – 46x – 3
9ax – 6bx + 8 + 4ax + 8bx – 7 – 6ax – 46x – 3
= 9ax + 4ax – 6ax – 6bx + 8bx – 4bx + 8 – 7 – 3
= 13ax – 6ax + 8bx – 10bx + 8 – 10
= 7ax – 2bx – 2
(viii)
abc + 2 ba + 3 ac, 4ca – 4ab + 2 bca and 2ab – 3abc – 6ac
abc + 2 ba + 3 ac + 4ca – 4ab + 2 bca + 2ab – 3abc – 6ac
= abc + 2abc – 3abc + 2ab – 4ab + 2ab + 3ca + 4ca – 6ca
= 3abc – 3abc + 4ab – 4ab + 7ca – 6ca
= 0 + 0 + ca = ca
(ix)
4a2 + 5b2 – 6ab, 3ab, 6a2 – 2b2 and 4b2 – 5 ab
4a2 + 5b2 – 6ab + 3ab, 6a2 – 2b2 + 4b2 – 5 ab
= 4a2 + 6a2 + 5b2 – 2b2 + 4b2 – 6ab + 3ab – 5ab
= 10a2 + 9b2 – 2b2 – 11ab + 3ab
= 10a2 + 7b2 – 8ab
(x)
x2 + x – 2, 2x – 3x2 + 5 and 2x2 – 5x + 7
= x2 + x – 2 + 2x – 3x2 + 5 + 2x2 – 5x + 7
= x2 – 3x2 + 2x2 + x + 2x – 5x – 2 + 5 + 7
= 3x2 – 3x2 + 3x – 5x – 2 + 12
= 0 – 2x + 10
= – 2x + 10
(xi)
4x3 + 2x2 – x + 1, 2x3 – 5x2 – 3x + 6, x2 + 8 and 5x3 – 7x
4x3 + 2x2 – x + 1 + 2x3 – 5x2 – 3x + 6 + x2 + 8 + 5x3 – 7x
= 4x3 + 2x3 + 5x3 + 2x2 – 5x2 + x2 – x – 3x – 7x + 1 + 6 + 8
= 11x3 + 3x2 – 5x2 – 11x + 15
= 11x3 – 2x2 – 11x + 15
Question 6.
Find the sum of:
(i) x and 3y
(ii) -2a and +5
(iii) – 4x2 and +7x
(iv) +4a and -7b
(v) x3+3x2y and 2y2
(vi) 11 and -by
Answer
(i) x + 3y
(ii) -2a + 5
(iii) – 4x2 + 7x
(iv) + 4a and -7b = 4a – 7b
(v) x3+3x2y and 2y2 = x3+ 3x2y + 2y2
(vi) 11 and -by = 11 – by
Question 7.
The sides of a triangle are 2x + 3y, x + 5y and 7x – 2y, find its perimeter.
Answer
Sides of a triangle are 2x + 3y, x + 5y, 7x – 2y
∴ Perimeter = sum of three sides of the triangle
= 2x + 3y + x + 5y + 7x – 2y
= 2x + x + 7x + 3y + 5y – 2y
= 10x + 8y – 2x
= 10x + 6y
Question 8.
The two adjacent sides of a rectangle are 6a + 96 and 8a – 46. Find its, perimeter.
Answer
Sides of a rectangle are 6a + 9b
and 8a – 4b
Let, length = 6a + 9b
and breadth = 8a – 4b
∴ Perimeter = 2 (l + b)
= 2 (6a + 9b + 8a – 4b)
= 2 (14 a + 5 b)
= 28a + 10b
Question 9.
Subtract the second expression from the first:
(i) 2a + b, a + b
(ii) – 2b + 2c, b + 3c
(iii) 5a + b, – 6b + 2a
(iv) a3 – 1 + a, 3a – 2a2
(v) p + 2, 1
(vi) x + 2y + z, – x – y – 3z
(vii) 3a2 – 8ab – 2b2 , 3a2 – 4ab + 6b2
(viii) 4pq – 6p2 – 2q2 , 9p2
(ix) 10abc, 2a2 + 2abc – 4b2
(x) a2 + ab + c2, a2 – d2
Answer
(i)
(2a + b) – (a + b)
= 2a + b – a – b
= 2a – a + b – b
= a + 0 = a
(ii)
(- 2b + 2c) + (b + 3c)
= – 2b + 2c – b – 3c
= – 2b – b + 2c – 3c
= – 3b – c
(iii)
(5a + b) – (- 6b + 2a)
= 5a + b + 6b – 2a
= 5a – 2a + b + 6b
= 3a + 7b
(iv)
(a3 – 1 + a) – (3a – 2a2)
= a3 – 1 + a – 3a + 2a2
= a3 + 2a2 – 2a – 1
(v) (p + 2) – 1 = p + 2 – 1 = p + 1
(vi)
(x + 2y + z) – (- x – y – 3z)
= x + 2y + z + x + y+ 3z
= x + x + 2y + y + z + 3z
= 2x + 3y + 4z
(vii)
(3a2 – 8ab – 2b2) – (3a2 – 4ab + 6b2 )
= 3a2 – 8ab – 2b2 – 3a2 + 4ab – 6b2
= 3a2 – 3a2 – 2b2 – 6b2 – 8ab + 4ab
= 0 – 8b2 – 4ab
= – 4ab – 8b2
(viii)
(4pq – 6p2 – 2q2) – (9p2)
= 4pq – 6p2 – 2q2 – 9p2
= 4pq – 15p2 – 2q2
(ix)
10abc – (2a2 + 2abc – 4b2 )
= 10 abc – 2a2 – 2abc + 4b2
= 10 abc – 2 abc – 2a2 + 4b2
= 8abc – 2a2 + 4b2
(x)
(a2 + ab + c2) – (a2 – d2 )
= a2 + ab + c2 – a2 + d2
= a2 – a2 + ab + c2 + d2
= ab + c2 + d2
Question 10.
Subtract:
(i) 4x from 8 – x
(ii) – 8c from c + 3d
(iii) – 5a – 2b from b + 6c
(iv) 4p + p2 from 3p2 – 8p
(v) 5a – 3b + 2c from 4a – b – 2c
(vi) – xy + yz – zx from xy – yz – xz
(vii) 2x2 – 7xy – y2 from 3x2 – 5xy + 3y2
(viii) a2 – 3ab – 6b2 from 2b2 – a2 + 2ab
(ix) 4x2 – 5x2y + y2 from – 3y2 + 5xy2 – 7x2 – 9x2y
(x) 6m3 + 4m2 + 7m – 3 from 3m3 + 4
Answer
(i)
4x from 8 – x
= (8 – x) – 4x
= 8 – x – 4x
= 8 – 5x
(ii)
– 8c from c + 3d
= (c + 3d) – (- 8c)
= c + 3d + 8c
= 9c + 3d
(iii)
– 5a – 2b from b + 6c
= (b + 6c) – (- 5a – 2b)
= b + 6c + 5a + 2b
= 5a + 3b + 6c
(iv)
4p + p2 from 3p2 – 8p
= (3p2 – 8p) – (4p + p2)
= 3p2 – 8p – 4p – p2
= 2p2 – 12p
(v)
5a – 3b + 2c from 4a – b – 2c
= (4a – b – 2c) – (5a – 3b + 2c)
= 4a – b – 2c – 5a + 3b – 2c
= 4a – 5a – b + 3b – 2c – 2c
= – a + 2b – 4c
(vi)
– xy + yz – zx from xy – yz – xz
= (xy – yz – xz) – (- xy + yz – xz)
= xy – yz + zx + xy – yz + xz
= xy + xy – yz – yz + zx + xz
= xy + xy – yz – yz + zx + xz
= 2(xy – yz + zx)
(vii)
2x2 – 7xy – y2 from 3x2 – 5xy + 3y2
= (3x2 – 5xy + 3y2) – (2x2 – 7xy – y2)
= 3x2 – 5xy + 3y2 – 2x2 + 7xy + y2
= 3x2 – 2x2 – 5xy + 7xy + 3y2 + y2
= x2 + 2xy + 4y2
(viii)
a2 – 3ab – 6b2 from 2b2 – a2 + 2ab
= (2b2 – a2 + 2ab) – (a2 – 3ab – 6b2)
= 2b2 – a2 + 2ab – a2 + 3ab + 6b2
= – a2 + a2 + 2b2 + 6b2 + 2ab + 3ab
= – 2a2 + 8b2 + 5ab
= 8b2 + 5ab – 2a2
(ix)
4x2 – 5x2y + y2 from – 3y2 + 5xy2 – 7x2 – 9x2y
= (- 3y2 + 5xy2 – 7x2 – 9x2y) – (4x2 – 5x2y + y2)
= – 3y2 + 5xy2 – 7x2 – 9x2y – 4x2 + 5x2y – y2
= – 3y2 – y2 + 5xy2 – 7×2 – 4x2 – 9x2y + 5x2y
= – 4y2 + 5xy2 – 11x2 – 4x2y
(x)
6m3 + 4m2 + 7m – 3 from 3m3 + 4
= (3m3 + 4) – (6m3 + 4m2 + 7m – 3)
= 3m3 + 4 – 6m3 + 4m2 + 7m – 3
= 3m3 – 6m3 – 4m2 – 7m + 4 + 3
= – 3m3 – 4m2 – 7m + 7
Question 11.
Subtract – 5a2 – 3a + 1 from the sum of 4a2 + 3 – 8a and 9a – 7.
Answer
sum of 4a2 + 3 – 8a and 9a – 7
= 4a2 + 3 – 8a + 9a – 7 = 4a2 + a – 4
∴ (4a2 + a – 4) – (- 5a2 – 3a + 1)
= 4a2 + a – 4 + 5a2 + 3a – 1
= 4a2 + 5a2 + a + 3a – 4 – 1
= 9a2 + 4a – 5
Question 12.
By how much does 8x3 – 6x2 + 9x – 10 exceed 4x3 + 2x2 + 7x -3 ?
Answer
8x3 – 6x2 + 9x – 10 exceeds 4x3 + 2x2 + 7x -3
= (8x3 – 6x2 + 9x – 10) – (4x3 + 2x2 + 7x – 3)
= 8x3 – 6x2 + 9x – 10 – 4x3 + 2x2 + 7x – 3
= 8x3 – 4x3 – 6x2 – 2x2 + 9x – 7x – 10 + 3
= 4x3 – 8x2 + 2x – 7
Question 13.
What must be added to 2a3 + 5a – a2 – 6 to get a2 – a – a3 + 1 ?
Answer
We get, the required result by subtracting
2a3 + 5a – a2 – 6 from – a3 + a2 – a + 1
= (- a3 + a2 – a + 1) – (2a3 – a2 + 5a – 6)
= – a3 + a2 – a + 1 – 2a3 + a2 – 5a + 6
= – a3 – 2a3 + a2 + a2 – a – 5a + 1 + 6
= – 3a3 + 2a2 – 6a + 7
Question 14.
What must be subtracted from a2 + b2 + lab to get – 4ab + 2b2 ?
Answer
We get, the required result by subtracting
– 4ab + 2b2 from a2 + b2 + 2ab
= a2 + b2 + 2ab – (- 4ab + 2b2)
= a2 + b2 + 2ab + 4ab – 2b2
= a2 + b2 – 2b2 + 2ab + 4ab
= a2 – b2 + 6ab
Question 15.
Find the excess of 4m2 + 4n2 + 4p2 over m2+ 3n2 – 5p2
Answer
The required result will be by substracting
m2+ 3n2 – 5p2 from 4m2 + 4n2 + 4p2
= 4m2 + 4n2 + 4p2 – (m2 + 3n2 – 5p2)
= 4m2 + 4n2 + 4p2 – m2 – 3n2 – 5p2
= 4m2 – m2 + 4n2 – 3n2 + 4p2 + 5p2
= 3m2 + n2 + 9p2
Question 16.
By how much is 3x3 – 2x2y + xy2 -y3 less than 4x3 – 3x2y – 7xy2 +2y3
Answer
We can get the required results by substracting
3x3 – 2x2y + xy2 -y3 from 4x3 – 3x2y – 7xy2 +2y3
= (4x3 – 3x2y – 7xy2 +2y3 ) – (3x3 – 2x2y + xy2 -y3)
= 4x3 – 3x2y – 7xy2 +2y3 – 3x3 + 2x2y – xy2 + y3
= 4x3 – 3x3 – 3x2y + 2x2y – 7xy2 – xy2 +2y3 + y3
= x3 – x2y – 8xy2 + 3y3
Question 17.
Subtract the sum of 3a2 – 2a + 5 and a2 – 5a – 7 from the sum of 5a2 -9a + 3 and 2a – a2 – 1
Answer
Sum of 3a2 – 2a + 5 and a2 – 5a – 7
= 3a2 – 2a + 5 + a2 – 5a – 7
= 3a2 + a2 – 2a – 5a + 5 – 7
= 4a2 – 7a – 2
and sum of 5a2 -9a + 3 and 2a – a2 – 1
= 5a2 – 9a + 3 + 2a – a2 – 1
= 5a2 – a2 – 9a + 2a + 3 – 1
= 4a2 – 7a + 2
Now (4a2 – 7a + 2) – (4a2 – 7a – 2)
= 4a2 – 7a + 2 – 4a2 + 7a + 2
= 4a2 – 4a2 – 7a + 7a + 2 + 2
= 0 + 0 + 4 = 4
Question 18.
The perimeter of a rectangle is 28x3+ 16x2 + 8x + 4. One of its sides is 8x2 + 4x. Find the other side
Answer
Perimeter of a rectangle (2l + 2b)
= 28x3 + 16x2 + 8x + 4
Let one side (l) = 8x2 + 4x
∴ 2l = 2 (8x2 + 4x) = 16x2 + 8x
∴ 2b = (28x3 + 16x2 + 8x + 4) – (16x2 + 8x)
= 28x3 + 16x2 + 8x + 4 – 16x2 – 8x
= 28x3 + 4
∴ Other side (b) = (28x3+4)/2
=14×3+2
Question 19.
The perimeter of a triangle is 14a2 + 20a + 13. Two of its sides are 3a2 + 5a + 1 and a2 + 10a – 6. Find its third side.
Answer
perimeter of a triangle = 14a2 + 20a + 13
Sum of two sides
= 3a2 + 5a + 1 + a2 + 10a – 6
= 3a2 + a2 + 5a + 10a + 1 – 6
= 4a2 + 15a – 5
∴ Third side = (14a2 + 20a + 13) – (4a2 + 15a – 5)
= 14a2 + 20a + 13 – 4a2 – 15a + 5
= 14a2 – 4a2 + 20a – 15a + 13 + 5
= 10a2 + 5a + 18
Question 20.
(i) If x = 4a2 + b2 – 6ab; y = 3b2 – 2a2 + 8ab and z = 6a2 + 8b2 – 6ab
find: x + y + z
(ii) If x = 4a2 + b2 – 6ab; y = 3b2 – 2a2 + 8ab and z = 6a2 + 8b2 – 6ab
find: x – y – z
Answer
(i)
x = 4a2 + b2 – 6ab
y = 3b2 – 2a2 + 8ab
z = 6a2 + 8b2 – 6ab
x + y + z
= 4a2 + b2 – 6ab + 3b2 – 2a2 + 8ab + 6a2 + 8b2 – 6ab
= 4a2 – 2a2 + 6a2 + b2 + 3b2 + 8b2 – 6ab + 8ab – 6ab
= 10a2 – 2a2 + 12b2 – 12ab + 8ab
= 8a2 + 12b2 – 4ab
(ii)
x = 4a2 + b2 – 6ab
y = 3b2 – 2a2 + 8ab
z = 6a2 + 8b2 – 6ab
x – y – z
= (4a2 + b2 – 6ab) – (3b2 – 2a2 + 8ab) – (6a2 + 8b2 – 6ab)
= 4a2 + b2 – 6ab – 3b2 + 2a2 – 8ab – 6a2 – 8b2 + 6ab
= 4a2 – 2a2 – 6a2 + b2 – 3b2 – 8b2 – 6ab – 8ab + 6ab
= 6a2 – 6a2 + b2 – 11b2 – 14ab + 6ab
= – 10b2 – 8ab
Question 21.

Answer
(i)
m = 9x2 – 4xy + 5y2
n = – 3x2 + 2xy – y2
∴ 2m – n
= 2 (9x2 – 4xy + 5y2) – (- 3x2 + 2xy – y2)
= 18x2 – 8xy + 10y2 + 3x2 – 2xy + y2
= 18x2 + 3x2 – 8xy – 2xy + 10y2 + y2
= 21x2 – 10xy + 11y2
(ii)
m = 9x2 – 4xy + 5y2
n = – 3x2 + 2xy – y2
∴ m + 2n
= (9x2 – 4xy + 5y2) + 2 (- 3x2 + 2xy – y2)
= 9x2 – 4xy + 5y2 – 6x2 + 4xy – 2y2
= 9x2 – 6x2 – 4xy + 4xy + 5y2 – 2y2
= 3x2 + 3y2
(iii)
m = 9x2 – 4xy + 5y2
n = – 3x2 + 2xy – y2
∴ m – 3n
= (9x2 – 4xy + 5y2) – 3 (- 3x2 + 2xy – y2)
= 9x2 – 4xy + 5y2 + 9x2 – 6xy + 3y2
= 18x2 – 10xy + 8y2
Question 22.
Simplify:

Answer
(i)
3x + 5(2x + 6) – 7x
⇒ 3x + 10x + 30 – 7x
⇒ 3x + 10x – 7x + 30
⇒ 13x – 7x + 30
⇒ 6x + 30
(ii)
3(4y – 10) 2(y – 1)
⇒ 12y – 30 + 2y – 2
⇒ 12y + 2y – 30 – 2
⇒ 14y – 32
(iii)
– (7 + 6x) – 7(x + 2)
⇒ – 7 – 6x – 7x – 14
⇒ – 7x – 6x – 7 – 14
⇒ -13 x – 21
(iv)
x – (x – y) – y – (y – x)
⇒ x – x + y – y – y + x
⇒ 2x – x – 2y + y
⇒ x – y
(v)
4x + 7y – (5y – 8) – 2x
⇒ 4x + 7y – 5y + 8 – 2x
⇒ 4x – 2x + 7y – 5y + 8
⇒ 2x + 2y + 8
(vi)
– 2m + 5 + 4(m – 3)
⇒ – 2m + 5 + 4m – 12
⇒ – 2m + 4m + 5 – 12
⇒ 2m – 7
(vii)
2x – y + 5 – (x – y)
⇒ 2x – y + 5 – (x – y)
⇒ 2x – x + 5
⇒ x + 5
(viii)
2(x – y) – (x – 8)
⇒ 2x – 2y – x + 8
⇒ 2x – x – 2y + 8
⇒ x – 2y + 8
(ix)
4(3x – 8) – 3(5x + 3) – 2(6x – 8)
⇒ 12x – 32 – 15x – 9 – 12x + 16
⇒ 12x – 15x – 12x – 32 – 9 + 16
⇒ 12x – 27x – 41 + 16
⇒ – 15 x – 25
(x)
5(x – 4) – 3(x – 4) + 7(x – 4)
⇒ 5x – 20 – 3x + 12 + 7x – 28
⇒ 5x + 7x – 3x + 12 + 7x – 28
⇒ 12x – 3x – 48 + 12
⇒ 9x – 36
Exe – 11 C Soved Questions of Fundamental Concepts for ICSE Class-7
Question 1.
Multiply:

Answer
(i)
Product of 3x, 5x2y and 2y
= 3x + 5x2y × 2y
= 3 × 5 × 2 × x × x2 × y × y
= 30x3y2
(ii)
Product of 5, 3a and 2ab2
= 5 × 3a × 2ab2
= 5 × 3 × 2 × a × ab2
= 30a2b2
(iii)
Product of 5x + 2y and 3xy
= 3xy (5x + 2y)
= 3xy × 5x + 3xy × 2y
= 15x2y + 6xy2
(iv)
Product of 6a – 5b and – 2a
= -2a (6a – 5b)
= – 2a × 6a + (- 2a) × (- 5b)
= – 12a2 + 10ab
(v)
Product of 4a + 5b and 4a – 5b
= 16a2 – 25b2
4a + 5b
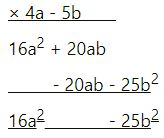
(vi)
Product of 9xy + 2y2 and 2x – 3y
= 18x2y – 23xy2 – 6y3
9xy + 2y2
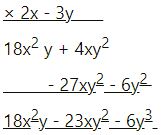
(vii)
Product of – 3m2n + 5mn – 4mn2 and 6m2n
= 6m2n (- 3m2n + 5mn – 4mn2 )
= 6m2n × (- 3m2n) + 6m2n × 5mn + 6m2n × (- 4mn2)
= 18m4n2 + 30m3n2 – 24 m3n3
(viii)
Product of 6xy2 – 7x2y2 + 10x3 and – 3x2y3
= – 3x2y3 (6xy2 – 7x2y2 + 10x3)
= – 3x2y3 × 6xy2 + (- 3x2y3) × (- 7x2y2 ) + (- 3x2y3) × 10x3
= – 18x3y5 + 21x4y5 – 30x5y3
Question 2.
Copy and complete the following multi-plications :

Answer
(i)
3a + 2b
× – 3xy
– 9axy – 6bxy
(ii)
9x + 5y
× – 3xy
– 27x2y + 15xy2
(iii)
3xy – 2x2 – 6x
× -5x2y
-15x3y2 + 10x4y + 30x3y
(iv)
a + b
× a + b
a2 + ab
ab + b2
a2 + 2ab + b2
(v)
ax – b
× 2ax + 2b2
2a2x2 – 2abx + 2ab2x – 2b3
(vi)
2a – b + 3c
× 2a – 4b
4a2 – 2ab + 6ac
– 8ab + 4b2 – 12bc
4a2 – 10ab + 6ac + 4b2 – 12bc
(vii)
3m2 + 6m – 2n
× 5n – 3m
15m2n + 30mn – 10n2 – 9m3 – 18m2
+ 6mn
15m2n + 36mn – 10n2 – 9m3 – 18m2
(viii)
6 – 3x + 2x2
× 1 + 5x – x2
6 – 3x + 2x2
+ 30x – 15x2 + 10x3
– 6x2 + 3x3 – 2x4
6 + 27x – 19x2 + 13x3 – 2x4
(ix)
4x3 – 10x2 + 6x – 8
× 3 + 2x – x2
12x3 – 30x2 + 18x – 24
8x4 – 20x3 + 12x2 – 16x
4x5 + 10x4 – 6x3 + 8x2
4x5 + 18x4 – 14x3 – 10x2 + 2x – 24
Question 3.
Evaluate :


Answer
(i)
(c + 5)(c – 3) = c (c – 3) +5 (c – 3)
= c2 – 3c + 5c – 15
= c2 + 2c – 15
(ii)
(3c – 5d)(4c – 6d)
= 3c (4c – 6d) – 5d(4c – 6d)
= 12c2 – 18cd – 20cd + 30d2
= 12c2 – 38cd + 30d2
(iii)
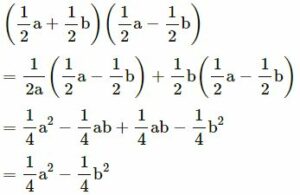
(iv)
(a2 + 2ab + b2)(a + b)
= a(a2 + 2ab + b2) + b(a2 + 2ab + b2)
= a3 + 2a2b + ab2 + a2b + 2ab2 + b3
= a3 + 3a2b + 3ab2 + b3
(v)
(3x – 1)(4x3 – 2x2 + 6x – 3)
= 3x (4x3 – 2x2 + 6x – 3) – 1 (4x3 – 2x2 + 6x – 3)
= 12x4 – 6x3 + 18x2 – 9x – 4x3 + 2x2 – 6x + 3
= 12x4 – 6x3 – 4x3 + 18x2 + 2x2 – 9x – 6x + 3
= 12x4 – 10x3 + 20x2 – 15x + 3
(vi)
(4m – 2)(m2 + 5m – 6)
= 4m (m2 + 5m – 6) – 2(m2 + 5m – 6)
= 4m3 + 20m2 – 24m – 2m2 – 10m + 12
= 4m3 + 20m2 – 2m2 – 24m – 10m + 12
= 4m3 + 18m2 – 34m + 12
(vii)
(8 – 12x + 7x2 – 6x3)(5 – 2x)
= 5(8 – 12x + 7x2 – 6x3) – 2x (8 – 12x + 7x2 – 6x3)
= 40 – 60x + 35x2 – 30x3 – 16x + 24x4 – 14x3 + 12x4
= 40 – 60x – 16x + 35x2 + 24x4 – 30x3 – 14x3 + 12x4
= 40 – 76x + 59x2 – 44x3 + 12x4
(viii)
(4x2 – 4x + 1)(2x3 – 3x2 + 2)
= 4x2 (2x3 – 3x2 + 2) – 4x (2x3 – 3x2 + 2) + 1 (2x3 – 3x2 + 2)
= 8x5 – 12x4 + 8x2 – 8x4 + 12x3 – 8x + 2x3 – 3x2 + 2
= 8x5 – 12x4 – 8x4 + 12x3 + 2x3 + 8x2 – 3x2 – 8x + 2
= 8x5 – 20x4 + 14x3 + 5x2 – 8x + 2
(ix)
(6p2 – 8pq + 2q2) (- 5p)
= -5p × 6p2 – 5p × (- 8pq) – 5p (2q2)
= – 30p3 + 40p2q – 10pq2
(x)
– 4y (15 + 12y – 8z) (x – 2y)
= – 4y (x – 2y)(15x + 12y – 8z)
= (- 4xy + 8y2)(15x + 12y – 8z)
= – 4xy (15x + 12y – 8z) + 8y2 (15x +12y – 8z)
= -60x2y – 48xy2 + 32xy + 120xy2 + 96y3 – 64y2z
= -60x2y – 48xy2 + 120xy2 – 64y2z + 96y3 + 32xy
= -60x2y + 72xy2 – 64y2z + 96y3 + 32xyz
(xi)
(a2 + b2 + c2 – ab – bc – ca)(a + b + c)
= a (a2 + b2 + c2 – ab – bc – ca) + b (a2 + b2 + c2 – ab – bc – ca) + c (a2 + b2 + c2 – ab – bc – ca)
= a3 + ab2 + ac2 – a2b – abc – ca2 +a2b + b3 + bc2 – ab2 – b2c – abc + a2c + b2c + c3 – abc – bc2 – c2a
= a3 + b3 + c3 -a2b + a2b – ca2 + a2c + bc2 – bc2 – ab2 + ab2 – abc – abc – abc + ac2 – ac2 + b2c – b2c
= a3 + b3 + c3 – 3abc
Question 4.
Evaluate:

Answer
(i)
(a + b)(a – b)
= a (a – b) + b(a – b)
= a2 – ab + ab – b2
= a2 – b2
(ii)
(a2 + b2)(a + b)(a – b)
= (a2 + b2)(a2 – b2) …{from(i)}
= a2 (a2 – b2) + b2 (a2 – b2)
= a4 – a2b2 + a2b2 – b4
= a8 – a4b4 + a4b4 – b8
= a4 – b4
(iii)
(a4 + b4)(a2 + b2)(a + b)(a – b)
= (a4 + b4) (a4 – b4) ….{from(ii)}
= a4 (a4 + b4) + b4 (a4 + b4)
= a8 – a4b4 + a4b4 – b8
= a8 – b8
Question 5.
Evaluate :

Answer
(i)
(3x – 2y)(4x + 3y)
= 3x (4x + 3y) – 2y (4x + 3y)
= 12x2 + 9xy – 8xy – 6y2
= 12x2 + xy – 6y2
(ii)
(3x – 2y)(4x + 3y)(8x – 5y)
= 3x (4x + 3y) – 2y (4x + 3y)(8x – 5y)
= (12x2 + 9xy – 8xy – 6y2 )(8x – 5y)
= (12x2 + xy – 6y2 )(8x – 5y)
= 8x (12x2 + xy – 6y2 ) – 5y (12x2 + xy – 6y2 )
= 96x3 + 8x2y – 48xy2 – 60x2y – 5xy2 + 30y3
= 96x3 + 8x2y – 60x2y – 48xy2 – 5xy2 + 30y3
= 96x3 – 52x2y – 53xy2 + 30y3
(iii)
(a + 5)(3a – 2)(5a + 1)
= {a (3a – 2) + 5(3a – 2)} (5a + 1)
= (3a2 – 2a + 15a – 10)(5a + 1)
= (3a2 + 13a – 10)(5a + 1)
= 5a (3a2 + 13a – 10) + 1 (3a2 + 13a – 10)
= 15a3 + 65a2 – 50a + 3a2 + 13a – 10
= 15a3 + 68a2 – 37a – 10
(iv)
(a + 1)(a2 – a + 1) and (a – 1)(a2 + a + 1)
= a (a2 – a + 1) + 1 (a2 – a + 1)
= a3 – a2 + a + a2 – a + 1
= a3 + 1
(a – 1)(a2 + a + 1)
= a(a2 + a + 1) – 1(a2 + a + 1)
= a3 + a2 + a – a2 – a – 1
= a3 – 1
Now, (a + 1)(a2 – a + 1) + (a – 1)(a2 + a + 1)
= a3 + 1 + a3 – 1
= 2a3
(v)
(5m – 2n)(5m + 2n)(25m2 + 4n2)
= {5m (5m + 2n) – 2n(5m + 2n)} (25m2 + 4n2)
= (25m2 + 10mn – 10mn – 4n2)(25m2 + 4n2)
= (25m2 – 4n2)(25m2 + 4n2)
= 25m2 (25m2 + 4n2) – 4n2 (25m2 + 4n2)
= 625m4 + 100m2n2 – 100m2n2 – 16n4
= 625m4 – 16n4
Question 6.
Multiply:

Answer
(i)
mn4, m3n and 5m2n3
⇒ 5m2n3 × mn4 × m3n
⇒5m2+1+3 n3+4+1
= 5m6n8
(ii)
2mnpq, 4mnpq and 5mnpq
⇒ 5mnpq × 2mnpq × 4mnpq
⇒5×2×4m1+1+1 n1+1+1 p1+1+1 q1+1+1
⇒ 40m3n3p3q3
(iii)
pq – pm and p2m
⇒ p2m × (pq – pm)
⇒ p3qm – p3m2
(iv)
x3 – 3y3 and 4x2y2
⇒ 4x2y2 × (x3 – 3y3)
⇒ 4x5y2 – 12x2y5
(v)
a3 – 4ab and 2a2b
⇒ 2a2b × (a3 – 4ab)
⇒ 2a5b – 8a3b2
(vi)
x2 + 5yx – 3y2 and 2x2y
⇒ 2x2y × (x2 + 5yx – 3y2)
⇒ 2x4y + 10x3y2 – 6x2y3
Question 7.
Multiply:

Answer
(i)
(2x + 3y)(2x + 3y)
⇒ 2x (2x + 3y) + 3y(2x + 3y)
⇒ 4x2 + 6xy + 6xy + 9y2
⇒ 4x2 + 12xy + 9y2
(ii)
(2x – 3y)(2x + 3y)
⇒ 2x (2x + 3y) – 3y(2x + 3y)
⇒ 2x × 2x + 2x × 3y – 3y × 2x – 3y × 3y
⇒ 4x2 + 6xy – 6xy – 9y2
⇒ 4x2 + 0 – 9y2
⇒ 4x2 – 9y2
(iii)
(2x – 3y)(2x + 3y)
⇒ 2x (2x + 3y) – 3y(2x + 3y)
⇒ 2x × 2x + 2x × 3y – 3y × 2x – 3y × 3y
⇒ 4x2 + 6xy – 6xy – 9y2
⇒ 4x2 + 0 – 9y2
⇒ 4x2 – 9y2
(iv)
(2x – 3y)(2x – 3y)
⇒ 2x (2x – 3y) – 3y(2x – 3y)
⇒ 2x × 2x – 2x × 3y + 3y × 2x + 3y × 3y
⇒ 4x2 – 6xy – 6xy + 9y2
⇒ 4x2 – 12xy + 9y2
(v)
(- 2x + 3y)(2x – 3y)
⇒ – 2x (2x – 3y) + 3y(2x – 3y)
⇒ – 4x2 + 6xy + 6xy – 9y2
⇒ – 4x2 + 12xy – 9y2
(vi)
(xy + 2b)(xy – 2b)
⇒ xy (xy – 2b) + 2b (xy – 2b)
⇒ x2y2 – 2bxy + 2bxy – 4b2
⇒ x2y2 – 4b2
(vii)
(x – a)(x + 3b)
⇒ x (x + 3b) – a (x + 3b)
⇒ x2 + 3bx – ax – 3ab
(viii)
(2x + 5y + 6)(3x + y – 8)
⇒ 2x (3x + y – 8) + 5y(3x + y – 8) + 6 (3x + y – 8)
⇒ 6x2 + 2xy – 16x + 15xy + 5y2 – 40y + 18x + 6y – 48
⇒ 6x2 + 2xy + 15xy – 16x + 18x + 5y2 – 40y + 6y – 48
⇒ 6x2 + 17xy + 2x + 5y2 – 34y – 48
(ix)
(3x – 5y + 2)(5x – 4y – 3)
⇒ 3x (5x – 4y – 3) – 5y (5x – 4y – 3) + 2 (5x – 4y – 3)
⇒ 15x2 – 12xy – 9x – 25xy + 20y2 + 15y + 10x – 8y – 6
⇒ 15x2 – 12xy – 25xy – 9x + 10x + 20y2 + 15y – 8y – 6
⇒ 15x2 – 37xy + x + 20y2 + 7y – 6
(x)
(6x – 2y)(3x – y)
⇒ 6x (3x – y) – 2y (3x – y)
⇒ 18x2 – 6xy – 6xy + 2y2
⇒ 18x2 – 12xy + 2y2
(xi)
(1 + 6x2 – 4x3)(-1 + 3x – 3x2)
⇒ 1(- 1 + 3x – 3x2) + 6x2 (- 1 + 3x – 3x2) – 4x3 (- 1 + 3x – 3x2)
⇒ – 1 + 3x – 3x2 – 6x2 + 18x3 – 18x4 + 4x3 – 12x4 + 12x5
⇒ – 1 + 3x – 9x2 + 22x3 – 30x4 + 12x5
ICSE Class-7 Concise Selina mathematics Solutions Exe- 11 D
Question 1.
Divide:


Answer
(i)
– 16ab2c by 6abc
=-16ab2c/6abc
=-(8/3)b
(ii)
25x2y by – 5y2
=25x2y/-5y2
=-5x2 /y
(iii)
8x + 24 by 4
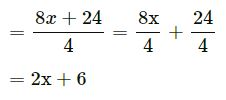
(iv)
4a2 – a by – a
= (4a2-a)/-a
= (4a2 /-a) – (a-a)
= – 4a + 1
(v)
8m – 16 by – 8
![]()
(vi)
– 50 + 40p by 10p
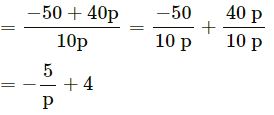
(vii) 4x3 – 2x2 by – x
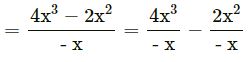
= – 4x2 + 2x
(viii)
10a3 – 15a2b by – 5a2
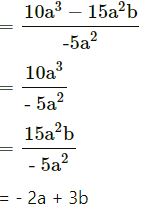
(ix) 12x3y – 8x2y2 + 4x2y3 by 4xy
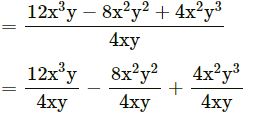
= 3x2 – 2xy + xy2
(x) 9a4b – 15a3b2 + 12a2b3 by – 3a2b
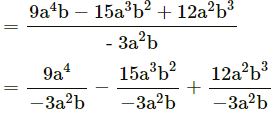
= – 3a2 + 5ab – 4b2
Question 2.
Divide :

Answer
(i)
9a4b – 15a3b2 + 12a2b3 by – 3a2b
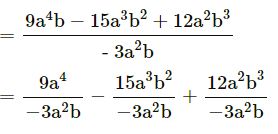
= – 3a2 + 5ab – 4b2
(ii)
m2 – 2mn + n2 by m – n
m – n
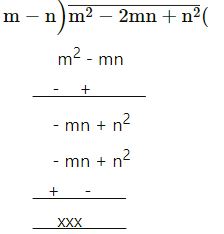
= m – n
(iii)
a2 + 4a + 1 by 2a + 1
2a + 1
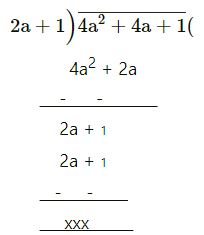
= 2a + 1
(iv)
p2 + 4p + 4 by p + 2
p + 2
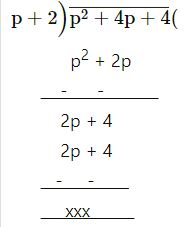
= p + 2
(v)
x2 + 4xy + 4y2 by x + 2y
x + 2y
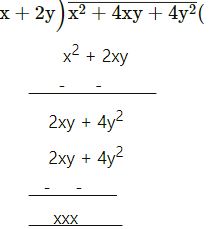
= x + 2y
(vi)
2a2 – 11a + 12 by a – 4
2a – 3
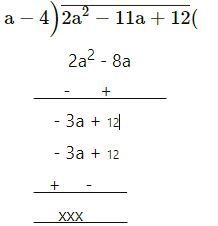
= 2a – 3
(vii)
6x2 + 5x – 6 by 2x + 3
3x – 2
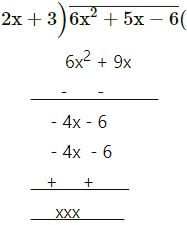
= 3x – 2
(viii)
8a2 + 4a – 60 by 2a – 5
4a + 12
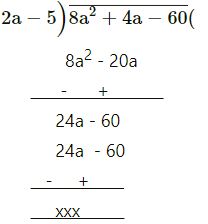
= 4a + 12
(ix)
9x2 – 24xy + 16y2 by 3x- 4y
3x – 4y
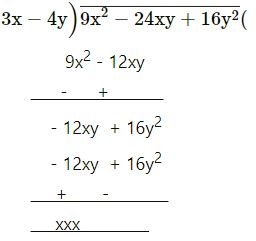
= 3x – 4y
(x)
15x2 + 31xy + 14y2 by 5x + 7y
3x + 2y
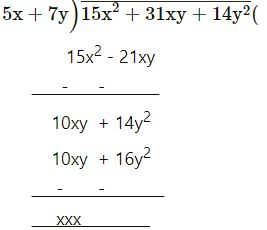
= 3x + 2y
(xi)
35a3 + 3a2b – 2ab2 by 5a – b
7a2 + 2ab
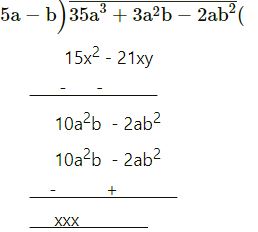
= 7a2 + 2ab
(xii)
6x3 + 5x2 – 21x + 10 by 3x – 2
2x2 + 3x – 5
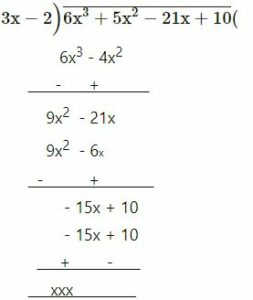
= 2x2 + 3x – 5
Question 3.
The area of a rectangle is 6x2– 4xy – 10y2 square unit and its length is 2x + 2y unit. Find its breadth
Answer
Area of a rectangle
= 6x2 – 4xy – 10y2 sq.units
Length = 2x + 2y units
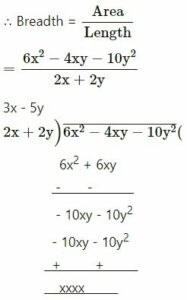
= 3x – 5y units
Hence breadth = 3x – 5y units
Question 4.
The area of a rectangular field is 25x2 + 20xy + 3y2 square unit. If its length is 5x + 3y unit, find its breadth, Hence find its perimeter.
Answer
Area of a rectangle
= 25x2 + 20xy + 3y2
Length = (5x + 3y) units
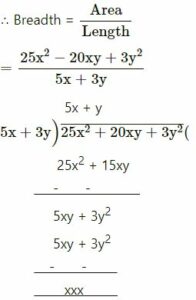
Hence Breadth = 5x + y
Hence perimeter of rectangular field
= 2 (l + b)
= 2 (5x + 3y + 5x + y)
= 2 (10x + 4y)
= 20x + 8y
Question 5.
Divide:

Answer
(i)
2m3n5 by – mn
= 2m3n5 / -mn
= – 2m2n4
(ii) 5x2 – 3x by x
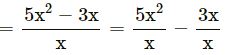
= 5x – 3
(iii) 10x3y – 9xy2 – 4x2y2 by xy
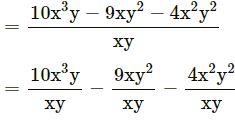
= 10x2 – 9y – 4xy
(iv)
3y3 – 9ay2 – 6ab2y by -3y
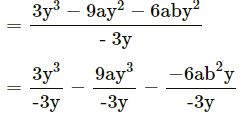
= – y2 + 3ay2 + 2ab2
(v)
x5 – 15x4 – 10x2 by -5x2
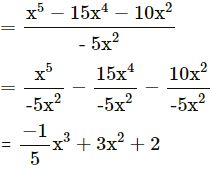
(vi) 12a2 + ax – 6x2 by 3a – 2x
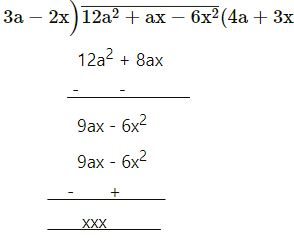
= 4a + 3x
(vii)
6x2 – xy – 35y2 by 2x – 5y
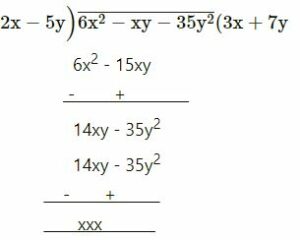
= 3x + 7y
(viii) x3 – 6x2 + 11x – 6 by x2 – 4x + 3
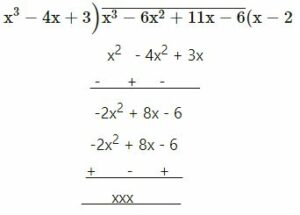
= x – 2
(ix)
m3 – 4m2 + m + 6 by m2 – m – 2
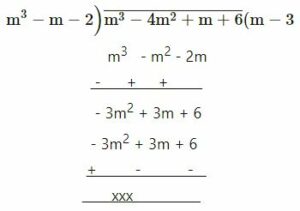
= m – 3
Fundamental Concepts ICSE Class-7 Exe- 11 E
Simplify
Question 1.

Answer
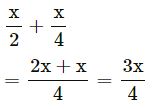
Question 2.
![]()
Answer
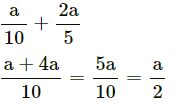
Question 3.

Answer
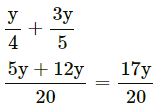
Question 4.

Answer
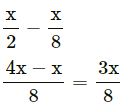
Question 5.

Answer
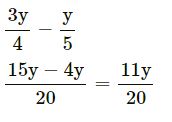
Question 6.

Answer
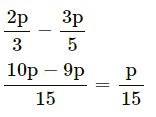
Question 7.

Answer

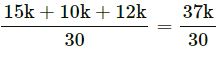
(LCM of 2, 3, 5 = 30)
Question 8.
![]()
Answer
![]()
(LCM of 5, 4 = 20)
![]()
Question 9.
![]()
Answer
![]()
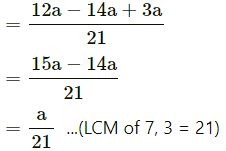
Question 10.
![]()
Answer
![]()
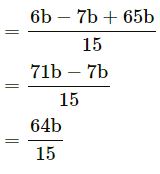
Question 11.
![]()
Answer
![]()

Question 12.

Answer

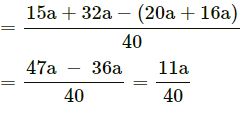
Question 13.
![]()
Answer
![]()
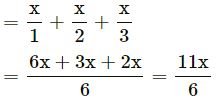
Question 14.
![]()
Answer
![]()
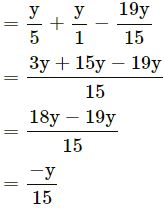
Question 15.
![]()
Answer
![]()
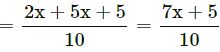
Question 16

Answer

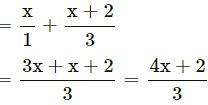
Question 17.

Answer

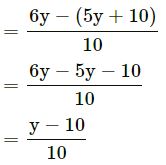
Question 18.
![]()
Answer
![]()
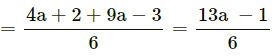
.(LCM of 3,2 = 6)
Question 19.

Answer

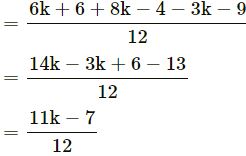
Question 20.

Answer

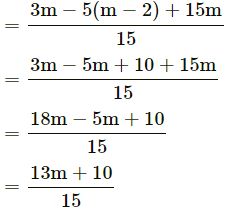
Question 21
.

Answer


Question 22.

Answer

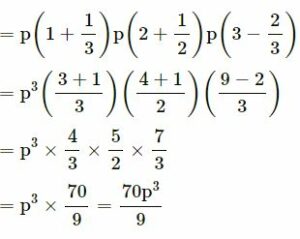
Question 23.
![]()
Answer
![]()
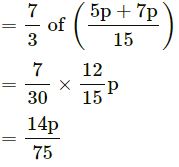
Question 24.

Answer

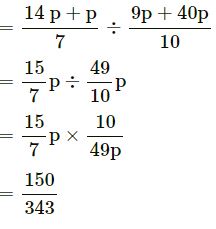
Question 25.

Answer

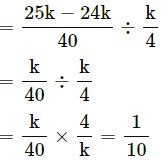
Question 26.

Answer

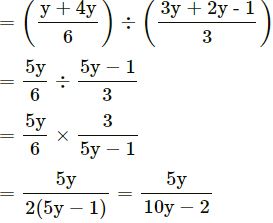
Exe – 11 F Concise Selina Maths ICSE Class-7
Enclose the given terms in brackets as required :
Question 1.
x – y – z = x-{…….)
Answer
x – y – z = x – (y + z)
Question 2.
x2 – xy2 – 2xy – y2 = x2 – (…….. )
Answer
x2 – xy2 – 2xy – y2
= x2 – (xy2 + 2xy + y2)
Question 3.
4a – 9 + 2b – 6 = 4a – (…….. )
Answer
4a – 9 + 2b – 6
= 4a – (9 – 2b + 6)
Question 4.
x2 -y2 + z2 + 3x – 2y = x2 – (…….. )
Answer
x2 -y2 + z2 + 3x – 2y
= x2 – (y2 – z2 – 3x + 2y)
Question 5.
– 2a2 + 4ab – 6a2b2 + 8ab2 = – 2a (……… )
Answer
– 2a2 + 4ab – 6a2b2 + 8ab2
= – 2a (a – 2b + 3ab2 – 4b2)
Simplify :
Question 6.
2x – (x + 2y- z)
Answer
2x – (x + 2y- z)
= 2x – x – 2y + z
= x – 2y + z
Question 7.
p + q – (p – q) + (2p – 3q)
Answer
p + q – (p – q) + (2p – 3q)
= p + q – p + q + 2p – 3q
= 2p – q
Question 8.
9x – (-4x + 5)
Answer
9x – (- 4x + 5)
= 9x + 4x – 5
= 13x – 5
Question 9.
6a – (- 5a – 8b) + (3a + b)
Answer
6a – (- 5a – 8b) + (3a + b)
= 6a + 5a + 8b + 3a + b
= 6a + 5a + 3a + 8b + b
= 14a + 9b
Question 10.
(p – 2q) – (3q – r)
Answer
(p – 2q) – (3q – r)
=p – 2q – 3q + r
=p – 5q + r
Question 11.
9a (2b – 3a + 7c)
Answer
9a (2b – 3a + 7c)
= 18ab – 27a2 + 63ca
Question 12.
-5m (-2m + 3n – 7p)
Answer
– 5m (-2m + 3n – 7p)
= – 5m x (-2m) + (-5m) (3n) – (-5m) (7p)
= 10m2 – 15mn + 35 mp.
Question 13.
-2x (x + y) + x2
Answer
– 2x (x + y) + x2
= -2x × x + (-2x)y + x2
= – 2x2 – 2xy + x2
= – 2x2 + x2 – 2xy = – x2 – 2xy
Question 14.

Answer

= b × 2b – b × (1/b) – 2b×b+2b×(1/b)
= 2b2 – 1 – 2b2 + 2
= 2b2 – 2b2 – 1 + 2
= 1
Question 15.
8 (2a + 3b – c) – 10 (a + 2b + 3c)
Answer
8 (2a + 3b – c) – 10 (a + 2b + 3c)
= 16a + 24b – 8c – 10a – 20b- 30c
= 16a – 10a + 24b – 20b – 8c – 30c
= 6a + 4b – 38c
Question 16.

Answer

= a2 + 1 – b2 + 1 – c2 – 1
= a2 – b2 – c2 + 1
Question 17.
5 x (2x + 3y) – 2x (x – 9y)
Answer
5 x (2x + 3y) – 2x (x – 9y)
= 10x2 + 15xy – 2x2 + 18xy
= 10x2 – 2x2 + 15xy+ 18xy
= 8x2 + 33xy
Question 18.
a + (b + c – d)
Answer
a + (b + c – d)
= a + (b + c – d)
= a + b + c – d
Question 19.
5 – 8x – 6 – x
Answer
5 – 8x – 6 – x
= 5 – 6 – 8x – x
= -1 – 7x
Question 20.
2a + (6- )
Answer
2a + (6- )
= 2a + (b – a + b)
= 2a + b – a + b
= a + 2b
Question 21.
3x + [4x – (6x – 3)]
Answer
3x + [4x – (6x – 3)]
= 3x + [4x – 6x + 3]
= 3x + 4x – 6x + 3
= 3x + 4x – 6x + 3
= 7x – 6x + 3
= x + 3
Question 22.
5b – {6a + (8 – b – a)}
Answer
5b – {6a + (8 – b – a)}
= 5b – 6a – 8 + b + a
= -6a + a + 5b +b – 8
= -5a + 6b – 8
Question 23.
2x-[5y- (3x -y) + x]
Answer
2x – [5y – (3x – y) + x]
= 2x – {5y – 3x +y + x}
= 2x – 5y + 3x -y – x
= 2x + 3x – x – 5y – y
= 4x – 6y
Question 24.
6a – 3 (a + b – 2)
Answer
6a – 3 (a + b – 2)
= 6a – 3a – 3b + 6
= 3a – 3b + 6
Question 25.
8 [m + 2n-p – 7 (2m -n + 3p)]
Answer
8 [m + 2n – p – 7 (2m – n + 3p)]
= 8 [m + 2n – p- 14m + 7n – 21p]
= 8m+ 16n – 8p – 112m + 56n – 168p
= 8m – 112m + 16n + 56n – 8p – 168p
= -104m + 72n – 176p
Question 26.
{9 – (4p – 6q)} – {3q – (5p – 10)}
Answer
{9 – (4p – 6q)} – {3q – (5p – 10)}
= {9 – 4p + 6q} – {3q -5p+ 10}
= 9 – 4p + 6q – 3q + 5p – 10
= 9 – 4p + 5p + 6q – 3q – 10
= p + 3q – 1
Question 27.
2 [a – 3 {a + 5 {a – 2) + 7}]
Answer
2 [a – 3 {a + 5 {a – 2) + 7}]
= 2 [a – 3 {a + 5a – 10 + 7}]
= 2 [a – 3a – 15a + 30 – 21]
= 2a – 6a – 30a + 60 – 42
= 2a – 36a + 60 – 42
= -34a + 18
Question 28.
5a – [6a – {9a – (10a – )}]
Answer
5a – [6a – {9a – (10a – )}]
= 5a – [6a – {9a – (10a – 4a + 3a)}]
= 5a – [6a – {9a – 10a + 4a – 3a}]
= 5a- [6a – 9a + 10a – 4a + 3a]
= 5a – 6a + 9a – 10a + 4a – 3a
= 5a + 9a + 4a – 6a – 10a – 3a
= 18a – 19a
= – a
Question 29.
9x + 5 – [4x – {3x – 2 (4x – 3)}]
Answer
9x + 5 – [4x – {3x – 2 (4x – 3)}]
= 9x + 5 – [4x – {3x – 8x + 6}]
= 9x + 5 – [4x – 3x + 8x – 6]
= 9x + 5-4x + 3x – 8x + 6
= 9x + 3x – 4x – 8x + 5 + 6
= 12x – 12x + 11
= 11
Question 30.
(x + y – z)x + (z + x – y)y – (x + y – z)z
Answer
(x + y – z)x + (z + x – y)y – (x + y – z)z
= x2+ xy – zx + yz + xy -y2 – zx – yz + z2
= x2 – y2 + z2 + 2xy – 2zx
Question 31.
-1 [a-3 {b -4 (a-b-8) + 4a} + 10]
Answer
-1 [a – 3 {b – 4 (a – b – 8) + 4a} + 10]
= -1 [a – 3 {b – 4{a – b – 8) + 4a} + 10]
= -1[a – 3 {b – 4a + Ab +32 + 4a} + 10]
= -1 [a – 3b + 12a – 126 – 96 – 12a + 10]
= -a + 3b – 12a + 12b + 96 + 12a – 10
= -a-12a + 12a+ 3b+ 12b – 96 – 10
= – a + 15b – 106
Question 32.
![]()
Answer
![]()
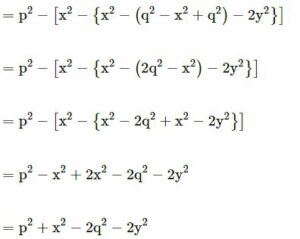
Question 33.
10 – {4a – (7 – ) – (5a –
)}
Answer
10 – {4a – (7 – ) – (5a –
)}
= 10 – {4a – (7 – a + 5) – (5a – 1 – a)}
= 10- {4a -(12 – a) -(4a – 1)}
= 10 – {4a – 12 + a- 4a + 1}
= 10 – 4a + 12 – a + 4a – 1
= 10 + 12 – 1 – 4a – a + 4a
= 21 – a
Question 34.
7a- [8a- (11a-(12a- )}]
Answer
7a- [8a- (11a-(12a- )}]
= 7a – [8a – {11a – (12a – 6a + 5a)}]
= 7a – [8a – {11a – (17a – 6a)}]
= 7a – [8a – {11a – (11a)}]
= 7a – [8a – {11a – 11a}]
= 7a – 8a
= – a
Question 35.
![]()
Answer
![]()
= 8x – [4y – {4x + (2x – 2y + 2x)}]
= 8x – [4y – {4x + (4x – 2y)}]
= 8x – [4y – {4x + 4x – 2y}]
= 8x – [4y – {4x – 4x + 2y}]
= 8x – [- 8x + 6y]
= 8x + 8x – 6y
= 16x – 6y
Question 36.
x-(3y- +2z-
)
Answer
x-(3y- +2z-
)
= x – (3y – 4z + 3x + 2z -5y + 7x)
= x – (- 2y – 2z + 10x)
= x + 2y + 2z – 10x
= – 9x + 2y + 2z
— End of Fundamental Concepts Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -7
Thanks