Gauss Theorem Numerical on Electric Flux Class-12 Nootan ISC Physics Solutions Ch-2. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-12 Physics.
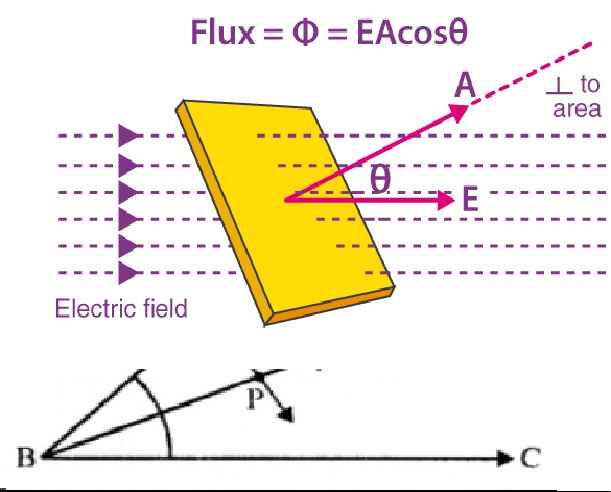
Gauss Theorem Numerical on Electric Flux Class-12 Nootan ISC Physics Solutions Ch-2
| Board | ISC |
| Class | 12 |
| Subject | Physics |
| Book | Nootan |
| Chapter-2 | Gauss Theorem |
| Topics | Numerical on Electric Flux |
| Academic Session | 2025-2026 |
Numerical on Electric Flux
Gauss Theorem Numerical on Electric Flux Class-12 Nootan ISC Physics Solutions Ch-2
Que-1. A point-charge of 1.8 µC is at the centre of a cubical Gaussian surface of 55 cm side. Find the net electric flux through the surface.
Ans-1 We use Gauss’ law: 𝜖0𝜙 = 𝑞,
where Φ is the total flux through the cube surface and q is the net charge inside the cube.
Thus,
𝜙 = 𝑞/𝜖0
= [(1.8×10^−6 𝐶)/(8.85×10^−12 𝐶²/𝑁.𝑚)]
= 2.0×10^5 𝑁.𝑚²/𝐶.
Que-2. The net outward electric flux through the surface of a box is 8.0 x 10^3 N m²/C. What is the net charge inside the box?
Ans-2 Given: Net outward flux through the surface of the box is 8× 10³ Nm²/C.
From Gausses law, the electric flux through the surface of the box is given as,
ϕ= q ε0
Where, q is the net charge of the body, and ε 0 is the permittivity of the free space.
By substituting the values in the above equation, we get
8× 10³ = q 8.854× 10^−12 q = 70.832× 10^−9 C
= 70.8 nC
Que-3. A point-charge produces an electric flux of -750 N m²/C through a spherical Gaussian surface of 10 cm radius with centre at the charge. (i) If the radius of the Gaussian surface be doubled, how much flux would pass through the surface? (ii) What is the magnitude of the point-charge?
Ans-3 (i) Total flux from a closed surface in independent of its size that is why total flux will remain unchanged
i.e., -750 Nm²/C
(ii) total charge = total flux x ε0
= -750 x 8.85 x 10^-12
= -6.64 x 10^-9 C.
Que-4. An isolated conductor of any shape has a net charge of +10 µC. Inside the conductor is a cavity within which is a point-charge of +3.0 µC. What is the charge on the cavity wall? On the outer surface of the conductor.
Ans-4 The inner surface of cavity will get -3μc charge dise to induction
∴ the outer surface will be reduced by -3μc charge
∴ charge on outer surface
= 10 – (-3) = 13μc.
Que-5. Given a uniform electric field E = 5 × 10^3 i N/C, find the electric flux of this field through a square of side 10 cm, whose plane is parallel to the YZ-plane. What would be the flux through the same square, if the plane of the square makes an angle of 30° with the X-axis?
Ans-5 Flux through a surface is given by:
ϕ = E.dS
Area is S = ES cos(90) = 0.1×0.1 = 0.01 m²
ϕ = 5×10³×0.01 = 50 Nm²/C
When the square makes an angle of 30o with the x-axis, angle made by the normal with electric field is 90°−30° = 60°
Hence, ϕ = ES cos(60°) = 25 Nm²/C.
Que-6. State Gauss’ law in electrostatic. A cube with each side ‘a’ meter is kept in an electric field given by E = Kxi, (as is shown in the figure) where K is a positive dimensional constant. Surface ABCD is parallel to Y-Z plane and surface CDEH is parallel to X-Z plane. Find out
(i) the electric flux through the cube, and
(ii) the net charge inside the cube.
Ans-6
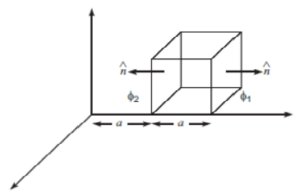
Net flux ø = ø1 + ø2
where ø1 = E.dS
2aC dS Cos0° = 2aC x a² = 2a³C
ø2 = aC x a² Cos180° = -a³C
ø = 2a³ C +(-a³C) = a³C Nm²/C
(ii) Net Charge = ε0 x ø = a³C ε0 coulomb
q = a³C ε0 coulomb
Que-7. A hollow cylindrical box of length 1 m and area of cross-section 25 cm² is placed in a three-dimensional coordinate system as shown in the figure. The electric field in the region is given by E = 50 xi, where E is in N/C and x is in metres. Find
(i) net flux through the cylinder.
(ii) charge enclosed by the cylinder.
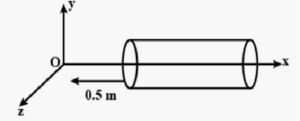
Ans-7 Area of the cross-section of the cylinder A = 25×10^−4 m¯²
Electric field at the face nearer to the origin E1 = 20×0.5 = 10 N/C
Thus flux entering through this face ϕ1 = E1A = 10×25×10^−4 = 2.5×10¯² Wb
Distance of second face from origin = 1+0.5 = 1.5 m
Electric field at the face away from the origin E2 = 20×(1.5) = 30 N/C
Thus flux leaving out through this face ϕ2 = E2A = 30×25×10^−4 = 7.5×10¯² Wb
(i) : Net flux through the cylinder ϕ = (7.5−2.5)×10¯² = 5×10¯² Wb
(ii) : Charge enclosed in the cylinder Q = ϕϵo
∴ Q = 5×10¯²×8.85×10¯¹² = 4.42×10¯¹³ C
— : End Gauss Theorem Numerical on Electric Flux Class-12 Nootan ISC Physics Solutions :–
Return to : – Nootan Solutions for ISC Class-12 Physics
Thanks
Please share with your friends


