HCF and LCM ICSE Class-6th Concise Selina Mathematics Solutions Chapter-8 . We provide step by step Solutions of Exercise / lesson-8 HCF and LCM for ICSE Class-6 Concise Selina Mathematics. Our Solutions contain all type Questions of Exe-8 A, Exe-8 B Exe-8 C and Exe-8 D to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-6 .
HCF and LCM ICSE Class-6th Concise Selina Maths Solutions Chapter-8
–: Select Topics :–
Exercise – 8 A of HCF and LCM Solved Questions for ICSE Class-6th Concise Selina Mathematics
Question- 1.
Write all the factors of :
(i) 15
(ii) 55
(iii) 48
(iv) 36
(v) 84
Answer-1
(i) Factors of 15 = F15 = 1, 3, 5 and 15
(ii) Factors of 55 = F55 = 1, 5, 11 and 55
(iii) Factors of 48 = F48 = 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48
(iv) Factors of 36 = F56 = 1, 2, 3, 4, 6, 9, 12, 18 and 36.
(v) Factors of 84 = F84 = 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42 and 84.
Question- 2.
Write all prime numbers :
(i) less than 25
(ii) between 15 and 35
(iii) between 8 and 76
Answer-2
(i) 2, 3, 5, 7, 11, 13, 17, 19 and 23
(ii) 17, 19, 23, 29 and 31
(iii) 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71 and 73
Question -3.
Write the prime-numbers from :
(i) 5 to 45
(ii) 2 to 32
(iii) 8 to 48
(iv) 9 to 59
Answer-3
(i) 7, 11, 13, 17, 19, 23, 29, 31, 37, 41 and 43.
(ii) 3, 5, 7, 11, 13, 17, 19, 23 29 and 31.
(iii) 11, 13, 17, 19, 23, 29, 31, 37, 41, 43 and 47.
(iv) 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47 and 53.
Question- 4.
Write the prime factors of:
(i) 16
(ii) 27
(iii) 35
(iv) 49
Answer-4
(i) Prime factors of 16 = 2

(ii) Prime factors of 27 = 3
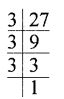
(iii) Prime factors of 35 = 5, 7
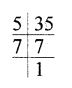
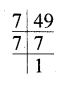
(iv) Prime factors of 49 = 7
Question- 5.
If Pn means prime factors of n, find:
(i) p6
(ii) P24
(iii) p50
(iv) P42
Answer-5
(i) F6 = 1, 2, 3, 6
P.F6 (Prime factor of 6) = 2 and 3.
(ii) F24 = 1, 2, 3, 4, 6, 8, 12, 24
P.F24 = 2 and 3.
(iii) F50 = 2, 5, 5
P.F50 = 2 and 5.
(iv) F42 = 1, 2, 3, 6, 7, 14, 21, 42
P.F42 = 2, 3 and 7.
Exercise – 8 B HCF and LCM Solutions for ICSE Class-6th Concise Selina Maths
Question- 1.
Using the common factor method, find the H.C.F. of :
(i) 16 and 35
(ii) 25 and 20
(iii) 27 and 75
(iv) 8, 12 and 18
(v) 24, 36, 45 and 60
Answer-1
(i) F16 = 1, 2, 4, 8, 16
F35 = 1, 5, 7, 35
Common factors between 16 and 35 = 1
H.C.F. of 16 and 35 = 1
(ii) F25 = 1, 5, 25
F20 = 1, 2, 4, 5, 10, 20
Common factors between 25 and 20 = 1, 5
H.C.F. of 25 and 20 = 5
(iii) F27 = 1, 3, 9, 27
F75 = 1, 3, 5, 15, 25, 75
Common factors between 27 and 75 = 1, 3
H.C.F. of 27 and 75 = 3
(iv) F8 = 1, 2, 4, 8
F12 = 1, 2, 3, 4, 6, 12
F18 = 1, 2, 3, 6, 9, 18
Common factors between 8, 12 and 18 = 1, 2
H.C.F. of 8, 12 and 18 = 2
(v) F24 = 1, 2, 3, 4, 6, 8, 12, 24
F36 = 1, 2, 3, 4, 6, 12, 18, 36
F45 = 1, 3, 5, 9, 15, 45
F60 = 1, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Common factor between 24, 36, 45 and 60 = 1, 3
H.C.F. of 24, 36, 45 and 60 = 3
Question -2.
Using the prime factor method, find the H.C.F. of:
(i) 5 and 8
(ii) 24 and 49
(iii) 40, 60 and 80
(iv) 48, 84 and 88
(v) 12, 16 and 28
Answer-2
(i) Prime factor of 5 = 5
Prime factor of 8 = 2 x 2 x 2
No common prime factor
H.C.F. of 5 and 8 = 1
(as both the number are co-prime)
(ii) Prime factor of 24 = 2 x 2 x 2 x 3
Prime factor of 49 = 7 x 7
No common prime factor, number are co-prime.
H.C.F. of 24 and 49 = 1.
(iii) Prime factor of 40 = 2 x 2 x 2 x 5
Prime factor of 60 = 2 x 2 x 3 x 5
Prime factor of 80 = 2 x 2 x 2 x 2 x 5
Common prime factor = 2 x 2 x 5
H.C.F. of 40, 60 and 80 = 2 x 2 x 5 = 20
(iv) Prime factor of 48 = 2 x 2 x 2 x 2 x 3
Prime factor of 84 = 2 x 2 x 3 x 7
Prime factor of 88 = 2 x 2 x 2 x 11
Common prime factor of 48, 84 and 88 = 2 x 2
H.C.F. of 48, 84 and 88 = 2 x 2 = 4
(v) Prime factor of 12 = 2 x 2 x 3
Prime factor of 16 = 2 x 2 x 2 x 2
Prime factor of 28 = 2 x 2 x 7
Common prime factor between 12, 16 and 28 = 2 x 2
H.C.F. of 12, 16 and 28 = 2 x 2 = 4
Question- 3.
Using the division method, find the H.C.F. of the following :
(i) 16 and 24
(ii) 18 and 30
(iii) 7, 14 and 24
(iv) 70,80,120 and 150
(v) 32, 56 and 46
Answer-3
(i) 16 and 24
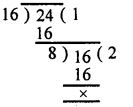
Since the last division is 8
Hence HCF of 16 and 24 = 8
(ii) 18 and 30
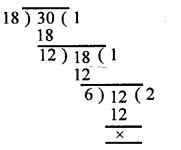
Since the last division is 6
Hence HCF of 18 and 30 = 6
(iii) 7, 14 and 24
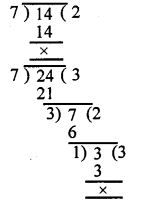
Since the last division is 1
Hence HCF of 7, 14 and 24 = 1
(iv) 70,80,120 and 150
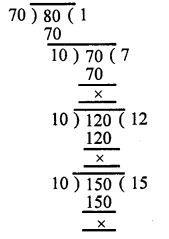
Since the last division is 10
Hence HCF of 70,80,120 and 150 = 10
(v) 32, 56 and 46

Since the last division is 2
Hence HCF of 32, 56 and 46 = 2
Question-4
Use a method of your own choice to find the H.C.F. of :
(i) 45, 75 and 135
(ii) 48, 36 and 96
(iii) 66, 33 and 132
(iv) 24, 36, 60 and 132
(v) 30, 60, 90 and 105
Answer-4
(i) Factor of 45 = F45 = 3 x 3 x 5
Factor of 75 = F75 = 3 x 5 x 5
and Factor of 135 = F135 = 3 x 3 x 3 x 5
Now the common factors of 45, 75 and 135 = 3 and 5
H.C.F. = 3 x 5 = 15
(ii) Factor of 48 = F48 = 2 x 2 x 2 x 2 x 3
Factor of 36 = F36 = 2 x 2 x 3 x 3
and factor of 96 = 2 x 2 x 2 x 2 x 2 x 3
Now the common factor of 48, 36 and 96 = 2, 2 and 3
H.C.F. = 2 x 2 x 3 = 12
(iii) Factor of 66 = F66 = 2 x 3 x 11
Factor of 33 = F33 = 3 x 11
and factor of 132 = F132 = 2 x 2 x 3 x 11
Now the common factor of 66, 33 and 132 = 3 and 11
H.C.F. = 3 x 11 =33
(iv) Factor of 24 = F24 = 2 x 2 x 2 x 3
Factor of 36 = F36 = 2 x 2 x 3 x 3
Factor of 60 = F60 = 2 x 2 x 3 x 5
and Factor of 132 = F132 = 2 x 2 x 3 x 11
Now the common factors of 24, 36, 60 and 132 = 2, 2 and 3
H.C.F. = 2 x 2 x 3 = 12
(v) Factor of 30 = F30 = 2 x 3 x 5
Factor of 60 = F60 = 2 x 2 x 3 x 5
Factor of 90 = F90 = 2 x 3 x 3 x 5
and factor of 105 = F105 = 3 x 5 x 7
Now the common factor of 30, 60, 90 and 105 = 3 and 5
H.C.F. = 3 x 5 = 15
Question -5.
Find the greatest number that divides each of 180, 225 and 315 completely.
Answer-5
The greatest number that divides 180, 225 and 315 will be HCF of 180, 225, 315
Let us first find HCF of 180 and 225
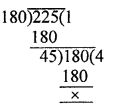
Since the third number is 315 and HCF of 180 and 225 is 45
Hence now to get HCF of 315 and 45

HCF of 180, 225, 315 = 45
Question -6.
Show that 45 and 56 are co-prime numbers.
Answer-6
The HCF of two co-prime numbers is always 1
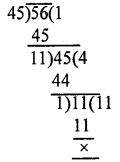
Because HCF of 45 and 56 is 1
Hence proved that 45 and 56 are co-prime numbers
Question- 7.
Out of 15, 16, 21 and 28, find out all the pairs of co-prime numbers.
Answer-7

Question- 8.
Find the greatest number. that will divide 93, 111 and 129, leaving remainder 3 in each case.
Answer-8
Since Remainder is 3 in each case numbers are
93 – 3 = 90
111 – 3 = 108
129 – 3 = 126
Required number will be HCF of 90,108 and 126
HCF of 90 and 108
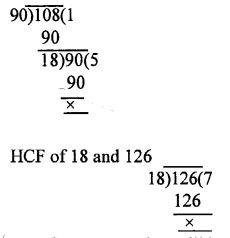
Hence the greatest number. that will divide 93, 111 and 129, leaving remainder 3 = 18
Exercise – 8 C HCF and LCM
Concise Maths Selina Solutions for ICSE Class-6
Question -1.
Using the common multiple method, find the L.C.M. of the following :
(i) 8, 12 and 24
(ii) 10, 15 and 20
(iii) 3, 6, 9 and 12
Answer-1

Question- 2.
Find the L.C.M. of each the following groups of numbers, using
(i) the prime factor method and
(ii) the common division method :
(i) 18, 24 and 96
(ii) 100, 150 and 200
(iii) 14, 21 and 98
(iv) 22, 121 and 33
(v) 34, 85 and 51
Answer-2
(i) L.C.M. of 18, 24 and 96
(i) By prime factors
Prime factors of 18 = 2 x 3 x 3
Prime factors of 24 = 2 x 2 x 2 x 3
Prime factors of 96 = 2 x 2 x 2 x 2 x 2 x 3
L.C.M. = 2 x 2 x 2 x 2 x 2 x 3 x 3 = 288
By common division method
L.C.M. of 18, 24 and 96 = 2 x 2 x 2 x 3 x 3 x 4 = 288





Question -3.
The H.C.F. and the L.C.M. of two numbers are 50 and 300 respectively. If one of the numbers is 150, find the other one.
Answer-3
H.C.F. = 50
L.C.M. = 300
Product of L.C.M. and H.C.F. = 300 x 50 = 15000
One number = 150
The other number
H.C.F. x L.C.M. = 1st number x 2nd Number
50. x 300. = 150 x 2nd Number
15000 = 150 x 2nd Number
150 x 2nd Number = 15000
2nd Number = 15000 / 150
2nd Number = 100
Question -4.
The product of two numbers is 432 and their L.C.M. is 72. Find their H.C.F.
Answer-4
Here, product of two number = 432
L.C.M. = 72
HCF = ?
Product of L.C.M. and H.C.F. = Product of two numbers
72 x HCF = 432
H.C.F. = 432 / 72 = 6
Question 5.
The product of two numbers is 19,200 and their H.C.F. is 40. Find their L.C.M.
Answer-5

Question- 6.
Find the smallest number which, when divided by 12, 15, 18, 24 and 36 leaves no remainder
Answer-6
The least number which is exactly divisible by each given number is their L.C.M.
Therefore Required number will be L.C.M. of 12, 15, 18, 24 and 36.

LCM =2 x 2 x 3 x 3 x 5 x 2
=360
Required number will be =360
Question -7.
Find the smallest number which, when increased by one is exactly divisible by 12, 18, 24, 32 and 40
Answer-7
First calculate LCM of 12, 18, 24, 32 and 40

LCM = 2 x 2 x 2 x 3 x 3 x 4 x 5
=1440
But Required Number = 1440 -1
= 1439
Question- 8.
Find the smallest number which, on being decreased by 3, is completely divisible by 18, 36, 32 and 27.
Answer-8
LCM of 18, 36, 32 and 27

LCM of 18, 36, 32 and 27 = 2 x 2 x 3 x3 x 8
LCM of 18, 36, 32 and 27 = 864
Hence Required Number = 864 + 3 = 867
Exercise – 8 D HCF and LCM ICSE Class-6th Revision Exercise
Question- 1.
Find the H.C.F. of :
(i) 108, 288 and 420
(ii) 36, 54 and 138
Answer-1
(i) H.C.F. of 108, 288, 420 = 12

Question- 2.
Find the L.C.M. of:
(i) 72, 80 and 252
(ii) 48, 66 and 120
Answer-2
(i) L.C.M. of 72, 80, 252

= 2 x 2 x 2 x 3 x 3 x 10 x 7
= 5040
(ii) LCM of 48, 66 and 120

= 2 x 2 x 2 x 2 x 3 x 5 x 11
= 2640
Question -3.
State true or false : Give an example.
(i) H.C.F. of two prime numbers is 1.
(ii) H.C.F. of two co-prime numbers is 1.
(iii) L.C.M. of two prime numbers is equal to their product.
(iv) L.C.M. of two co-prime numbers is equal to their product.
Answer-3
(i) True : Because the prime numbers have no common factor except 1.
(ii) True : Becuase co-prime numbers have no common factor except 1.
(iii) True : Because the prime number have no common factor except 1.
(iv) True : Because co-prime numbers have no common factor except 1.
Question -4.
The product of two numbers is 12096 and their H.C.F. is 36. Find their L.C.M.
Answer-4
product of two numbers = 12096
H.C.F. = 36
L.C.M. = ?
We know that
Product of two numbers = Product of their H.C.F. and L.C.M.
=> 12096 = 36 x L.C.M.
=> L.C.M. = 12096 / 36
= 336
Question -5.
The product of the H.C.F. and the L.C.M. of two numbers is 1152. If one number is 48, find the other one.
Answer-5
We know that:
Product of two numbers = Product of their H.C.F. and L.C.M.
=> 1st number x 2nd number = Product of their H.C.F. and L.C.M.
=> 48 x 2nd number = 1152
=> 2nd number = 1152 / 48 = 24
Question- 6.
(i) Find the smallest number that is completely divisible by 28 and 42.
(ii) Find the largest number that can divide 28 and 42 completely.
Answer-6
We know that the least number which is divisible by 28 and 42 is their L.C.M.

L.C.M. of 28 and 42 = 2 x 2 x 3 x 7 = 84
(ii) We know that the largest number which can divide 28 and 42 completely will be their H.C.F.
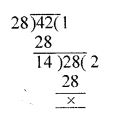
H.C.F. of 28 and 42 = 14
Question- 7.
Find the L.C.M. of 140 and 168. Use the L.C.M. obtained to find the H.C.F. of the given numbers.
Answer-7
Numbers are 140 and 168
L.C.M. of 140 and 168

Question- 8.
Find the H.C.F. of 108 and 450 and use the H.C.F. obtained to find the L.C.M. of the given numbers.
Answer-8
Numbers are given : 108 and 450
H.C.F. of 108 and 450= 18

— End of HCF and LCM ICSE Class-6th Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -6
Thanks


