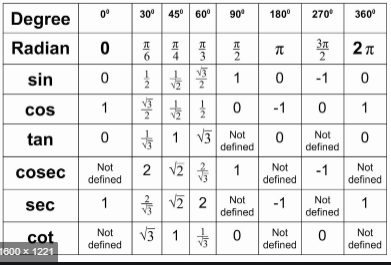
Height and Distances Chapter-22 Concise Solutions Class 10. Solutions of Exercise – 22 (A), Exercise –22 (B), Exercise – 22 (C) for Concise Selina Maths of ICSE Board Class 10th. Concise Maths Solutions Height and Distances Chapter-22 for ICSE Maths Class 10 is available here. All Solutions of Concise Selina Maths of Height and Distances Chapter-22 has solved. This is the Solutions of Height and Distances of Chapter-22 for ICSE Class 10th.
Height and Distances Chapter-22 Concise Solutions ICSE Maths Class 10
The Step by Step Solutions of Concise Mathematics Height and Distances Chapter-22 . Experience teachers Solved Height and Distances Chapter-22 to help students of class 10th ICSE board.
–: Select Topics:–
Exercise – 22 (A), Exercise –22 (B), Exercise – 22 (C)
How to Solve Height and Distances Chapter-22 Concise Maths
Note :- Before viewing Solutions of Height and Distances Chapter-22 of Concise Selina Maths. Read the Chapter Carefully and try to understand the Concept of Angle of elevation and Angle of Depression .Then solve all example of your text book. The Height and Distances Chapter-22 is main Chapter in ICSE board
Exercise-22(A) Height and Distances Chapter-22 Selina Concise Maths Solutions for ICSE Class 10
Question 1.
The height of a tree is 
Answer 1
Let AB be the tree and BC be its shadow.
∴ θ = 60°
∵ Angle of elevation of the sun = 60°
Question 2.
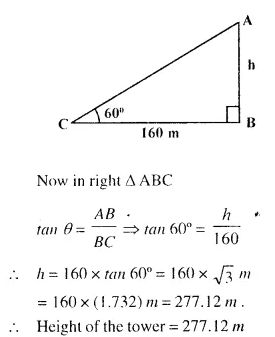
The angle of elevation of the top of a tower, from a point on the ground and at a distance of 160 m from its foot, is found to be 60°. Find the height of the tower.
Answer 2
Let AB be the tower and C is the point which is 160 m away from the foot of the tower,
i.e. CB = 160 m
Let height of the tower be x
Question 3.
A ladder is placed along a wall such that its upper end is resting against a vertical wall. The foot of the ladder is 2.4 m from the wall and the ladder is making an angle of 68“ with the ground. Find the height, upto which the ladder reaches.
Answer 3
Let AB be the wall and
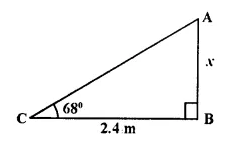
AC be the ladder, which is placed against the wall. If foot is 2.4 m away from the wall i.e. CB = 2.4m1.
Let AB =x m.
In right ∆ ABC,
tan θ = 
∴ x = 2.4 x tan 68° = 2.4 x 2.4751
= 5.94 m
Question 4.
Two persons are standing on the opposite sides of a tower. They observe the angles of elevation of the top of the tower to be 30° and 38° respectively. Find the distance between them, if the height of the tower is 50 m.
Answer 4
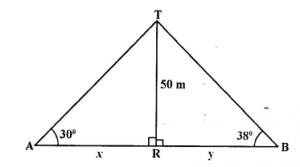
Two persons A and B are standing on the opposite side of the tower TR and height of tower TR = 50 m and angles of elevation with A and B are 30° and 38° respectively. Let AR = x and RB = y
Now in right ∆TAR,
Question 5.
A kite is attached to a string. Find the length of the string, when the height of the kite is 60 m. and the string makes an angle 30° with the ground.
Answer 5
Let KT be the height of kite and PK is the string which makes an angle of 30° with the ground.
∴ KT = 60 m
Let KP = xm.
Now in right ∆PKT,
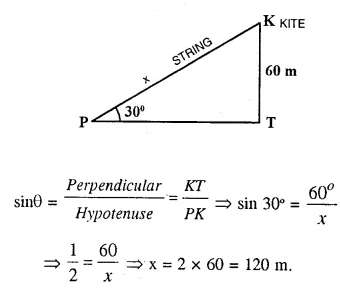
Question 6.
A boy 1.6m tall, is 20 m away from a tower and observes the angle of elevation of the top of the tower to be (i) 45° (ii) 60°. Find the height of the tower in each case.
Answer 6
(i) Let AB be the tower and MN be the boy who is 20m away from the foot of the tower.
Let AB = x and angle of elevation = 45°
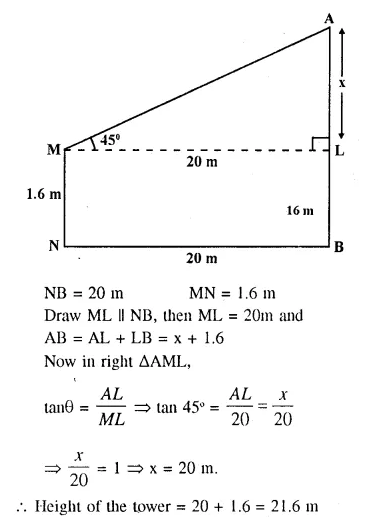
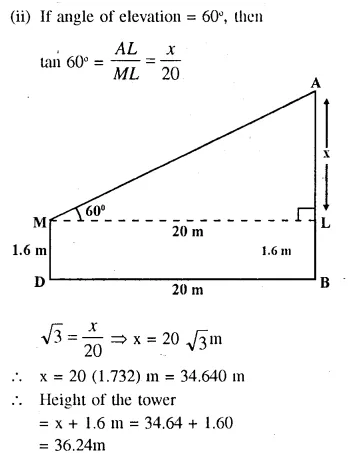
Question 7.
The upper part of a tree, broken over by the wind, makes an angle of 45° with the ground; and the distance from the root to the point where the top of the tree touches the ground, is 15m. What was the height of the tree before it was broken ?
Answer 7
Let AB be the tree which was broken at the point C which makes an angle of elevation of 45°, with the ground at a distance of 15m.
BD = 15m
AC = CD
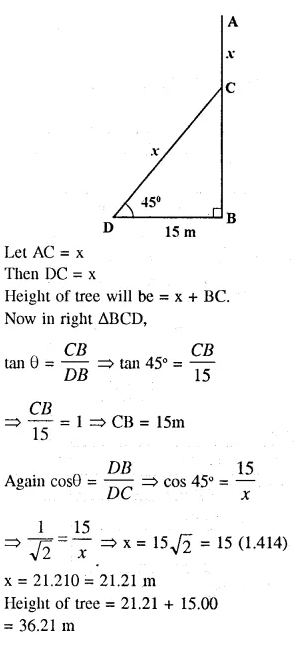
Question 8.
The angle of elevation of the top of an unfinished tower at a point distance 80 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60° ?
Answer 8
Distance of a point from the tower = 80 m
Angle of elevation = 30°
In second case the elevation of lower = 60°
In first case,
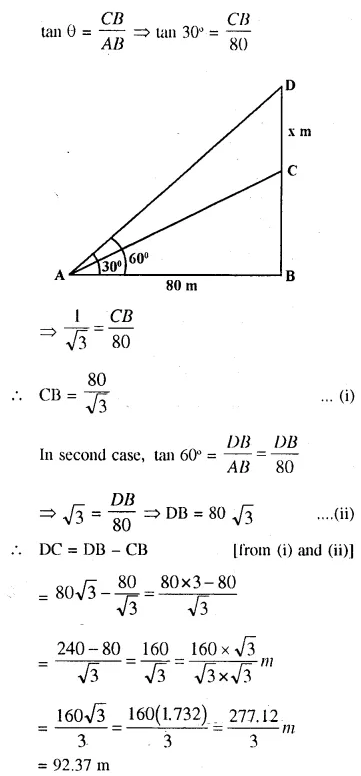
Question 9.
At a particular time, when the sun’s altitude is 30°, the length of the shadow of’C vertical tower is 45 m. Calculate :
(i) height of the tower.
(ii) the length of the shadow of the same tower, when the sun’s altitude is (a) 45° (b) 60°.
Answer 9
Shadow of the tower = 45 m and angle of elevation = 30°
Let AB be the lower and BC is its shadow.
∴ CB = 45 m.
Now in right ∆ABC,
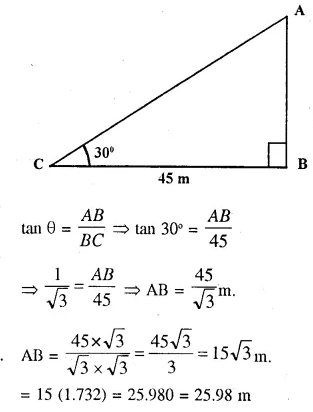
(ii) In second case,
(a) Angle of elevation = 45°
and height of tower = 25.98 m or 15
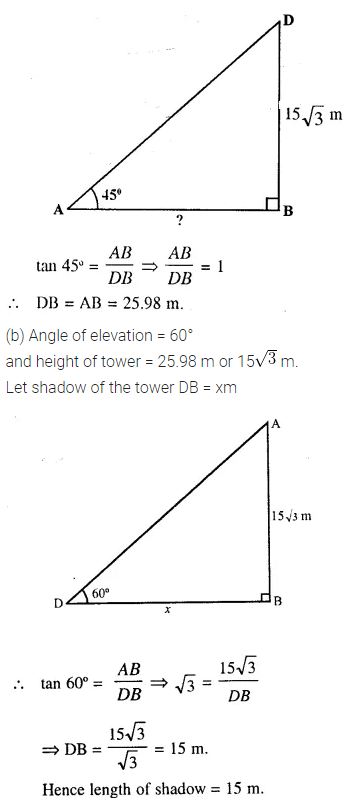
Question 10.
Two vertical poles are on either side of a road. A 30 m long ladder is placed between the two poles. When the ladder rests against one pole, it makes angle 32°24′ with the pole and when it is turned to rest against another pole, it makes angle 32°24′ with the road. Calculate the width of the road.
Answer 10
Two poles AB and CD which are at the either end of a road BD. A ladder 30 m long subtends an angle of 32° 24′ with the first pole AB and 32°24′ with the road when it is turned to rest against the second pole CD.
Now in right ∆ABE.
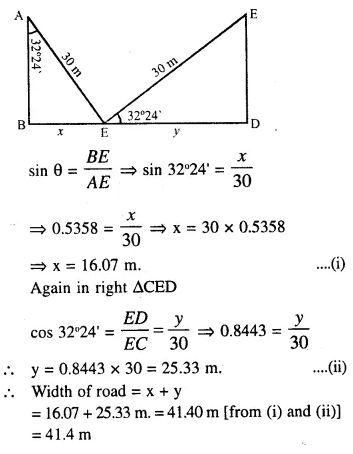
Question 11.
Two climbers are at points A and Bona vertical cliff face. To an observer C, 40 m from the foot of the cliff on the level ground, A is at an elevation of 48° and B of 57°. What is the distance between the climbers ?
Answer 11
A and B are two climbers on the cliff and ob-server is at C, 40 m from the foot of the cliff while the angles of elevations of each climber is 48° and 57° respectively.
In right ∆ACD,
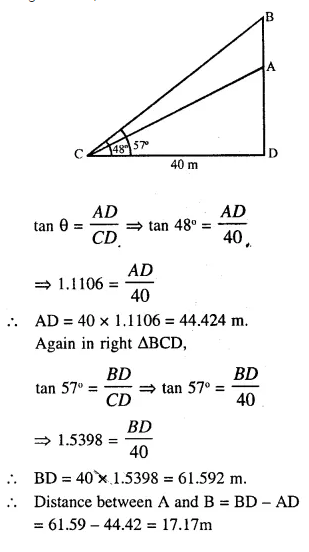
Question 12.
A man stands 9m away from a flag-pole. He observes that angle of elevation of the top of the pole is 28° and the angle of depression of the bottom of the pole is 13°. Calculate the height of the pole.
Answer 12
Let PL is the pole and MN is the man The angle of elevation of the top of the pole = 28°
arid the angle of depression of the bottom of the pole =13°
Man is 9 m away from the pole,
i.e. MQ = 9 m
Now in right ∆PMQ,
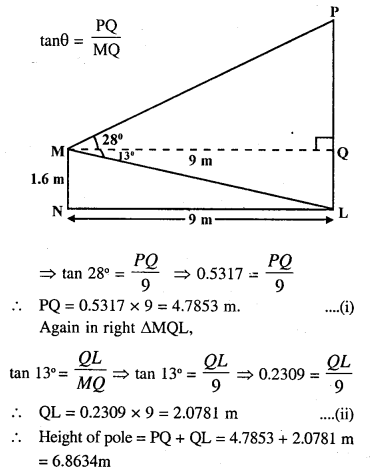
Question 13.
From the top of a cliff 92 m high, the angle of depression of a buoy is 20°. Calculate to the nearest metre the distance of the buoy from the foot of the cliff.
Answer 13
Let CD be the cliff and CD = 92m, B is the buoy,
then from C ,
the angle of depression is 20°
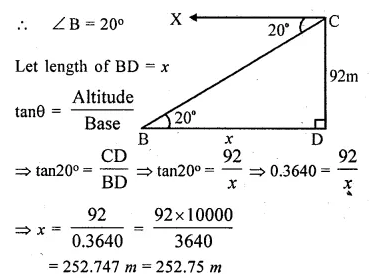
Height and Distances Exercise-22(B) Chapter-22 Selina Concise Maths Solutions for ICSE Class 10
Question 1.
In the figure given below, it is given that AB is perpendicular to BD and is of length X metres. DC = 30 m. ∠ADB = 30° and ∠ACB = 45°. Without using tables, find X.
Answer 1
Question 2.
Find the height of a tree when it is found that on walking away from it 20m, in a horizontal line through its base, the elevation of its top Changes from 60° to 30°.
Answer 2
Let AB be the tree and its height be x DC = 20 m.
Now in right ∆ADB
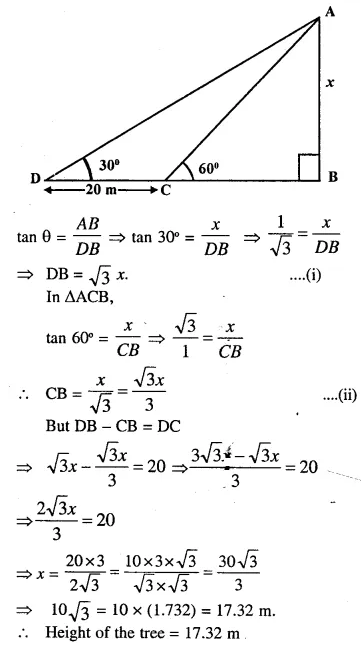
Question 3.
Find the height of a building, when it is found that on walking towards it 40 m in a horizontal line through its base the angular elevation of its top changes from 30° to 45°.
Answer 3
Let AB be the building and its
height be x and DC =40m
Now in right ∆ADB
Question 4.
From the top of a light house 100 m high, the angles of depression of two ships are observed as 48° and 36° respectively. Find the distance between the two ships (in the nearest metre) if :
(i) the ships are on the same side of the light house,
(ii) the ships are on the opposite sides of the light house.
Answer 4
AD = 100 m
In right angled ∆ABD
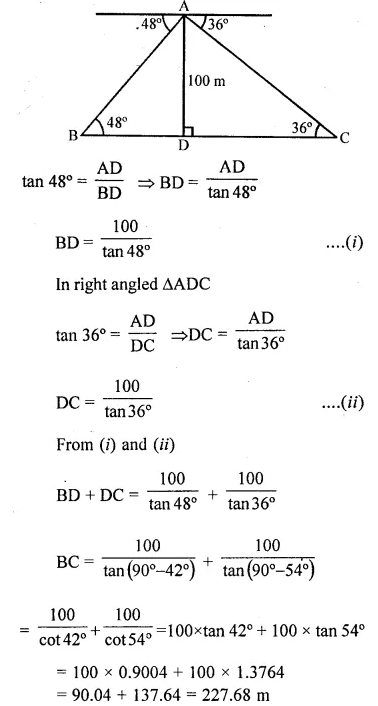
Question 5.
Two pillars of equal heights stand 011 either side of a roadway, which is 150m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60° and 30”; find the height of the pillars and the position of the point.
Answer 5
Let AB and CD be the two pillars which stand on either side of a road BD,
Then BD = 150m
Let AB = CD = h
and Let P be the point on the road such that the angles of elevation from P to the top of the pillars are 60° and 30° respectively.
Let BP = x then PD = 150 – x
Question 6.
From the figure given below, calculate the length of CD.
Answer 6
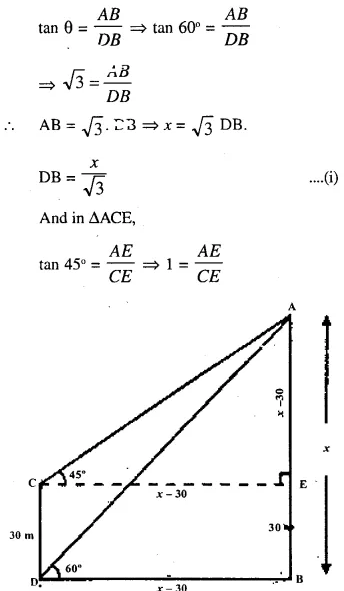
Question 7.
The angle of elevation of the top of a tower is observed to be 60°. At a point 30 m vertically above the first point of observation, the elevation is found to be 45°. Find :
(i) the height of the tower,
(ii) its horizontal distance from the points of observation.
Answer 7
Let height of tower = x i.e. AB = x
In the right ∆ADB,
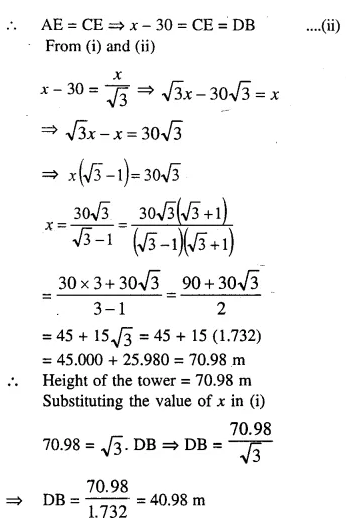
Question 8.
From the top of a cliff. 60 metre high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°. Find the height of the tower.
Answer 8
Height of the cliff AB = 60m
Let the height of tower = x
Draw TR 
Question 9.
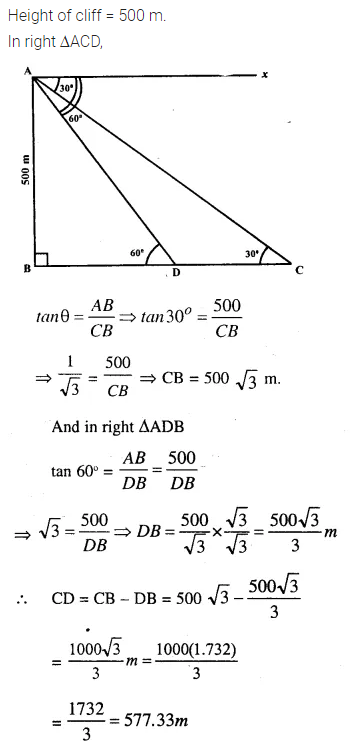
A man on a cliff observes a boat, at an angle of depression 30°, which is sailing towards the shore to the point immediately beneath him. Three minutes later the angle of depression of the boat is found to be 60°. Assuming that the boat sails at a uniform speed, determine :
(i) how much more time it will take to reach the shore.
(ii) the speed of the boat in metre per second, if the height of the cliff is 500 m.
Answer 9
Height of cliff = 500 m.
In right ∆ACD,
Question 10.
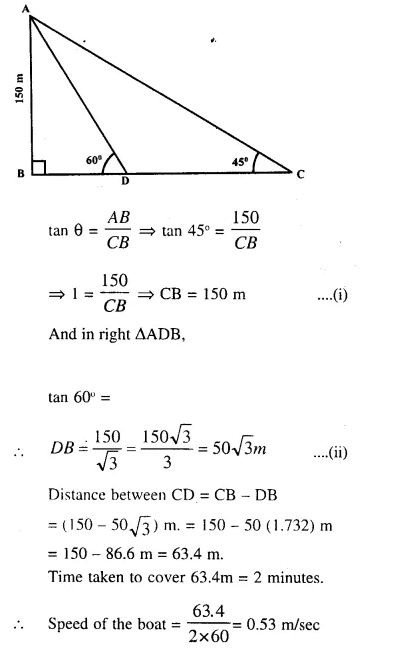
A man in a boat rowing away from a light house 150m high, takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 45°. Find the speed of the boat.
Answer 10
Height of the lighthouse AB = 150m
Now is right ∆ACB,
Question 11.
A person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 m away from the bank, he finds the angle of elevation to be 30°. Find :
(i) the height of the tree, correct to 2 decimal places,
(ii) the width of the river.
Answer 11
TR is the height of tree and RQ is the width of the river.
Let TR = x
Now in right ∆TQR
Question 12.
The horizontal distance between two towers is 75 m and the angular depression of the top of the first tower as seen from the top of the second, which is 160m high, is 45°. Find the height of the first tower.
Answer 12
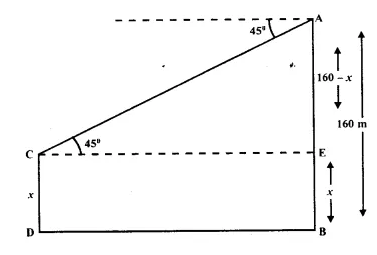
Let the height of first tower CD = x
and height of second tower AB = 160 m
Distance between them DB = 75 m.
In right ∆ACE,
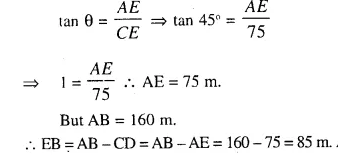
Question 13.
The length of the shadow of a tower standing on level plane is found to be 2y metres longer when the sun’s altitude is 30″ than when it was
45°. Prove that the height of the tower is y (
Answer 13
Let AB be the tower and AB = x
Distance CD = 2y
In right ∆ADB,
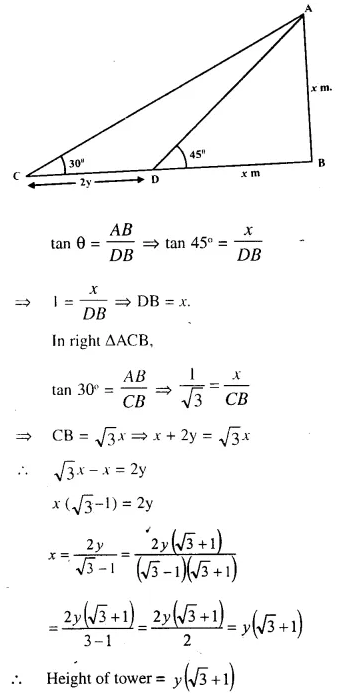
Question 14.
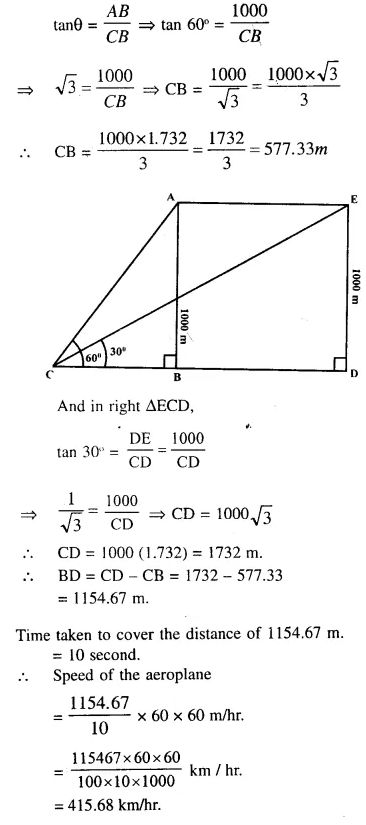
An aeroplane flying horizontally 1 km above the ground and going away from the observer is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°, find the uniform speed of the aeroplane in km per hour.
Answer 14
Height of aeroplane = 1 km = 1000 m.
In right ∆ACB,
Question 15.
From the top of a hill, the angles of depression of two consecutive kilometre stones, due east, are found to be 30° and 45° respectively. Find the distance of the two stones from the foot of the hill. (2007)
Answer 15
Solutions of Concise Maths Height and Distances Chapter-22 EXERCISE – 22 (C)
Question 1.
Find AD.
Answer 1
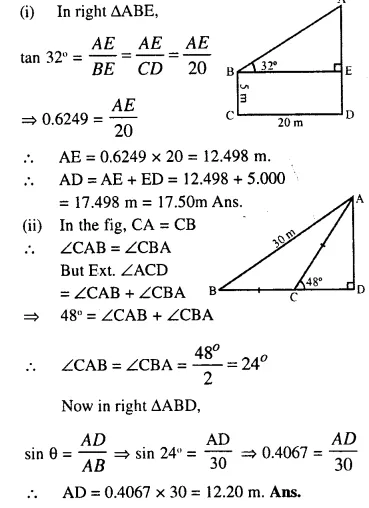
Question 2.
In the following diagram.
AB is a floor-board. PQRS is a cubical box with each edge = 1 m and ∠B = 60°. Calculate the length of the board AB.
Answer 2
Question 3.
Calculate BC.
Answer 3
Question 4.
Calculate AB .
Answer 4
Question 5.
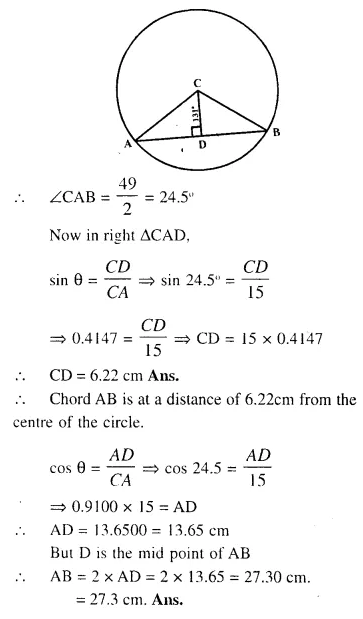
The radius of a circle is given as 15cm and chord AB subtends an angle of 131° at the centre C of the circle. Using trigonometry, Calculate :
(i) the length of AB;
(ii) the distance of AB from the centre C.
Answer 5
Chord AD substends an angle of 131° at the centre. Join CA, CB and draw CD ⊥ AB which bisects AB at D.
(In ∆CAB)
∵ CA = CB (radii of the same circle)
∴ ∠CAB = ∠CBA
But ∠CAB + ∠CBA = 180°- 131° = 49°
Question 6.
At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is 
Answer 6
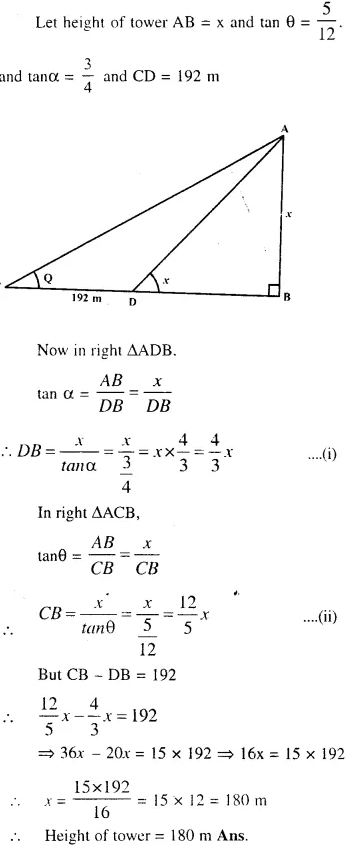
Question 7.
A vertical tower stands on horizontal plane and is surmounted by a vertical flagstaff of height h metre. At a point on the plane, the angle of elevation of the bottom of the flagstaff is a and that of the top of flagstaff is β. Prove that the height of the tower is :
Answer 7
Question 8.
With reference to the given figure, a man stands on the ground at point A, which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m.
The man’s eye is 2 m above the ground. He observes the angle of elevation of C. The top of the pole, as x°, where tan x° = 
(i) the distance AB in m;
(ii) the angle of elevation of the top of the pole
when he is standing 15 m from the pole. Give your answer to the nearest degree. [1999]
Answer 8
Question 9.
The angles of elevation of the top of a tower from two points on the ground at distances a and b metres from the base of the tower and in the same striaght line with it are complementary.Prove that height of the tower is 
Answer 9
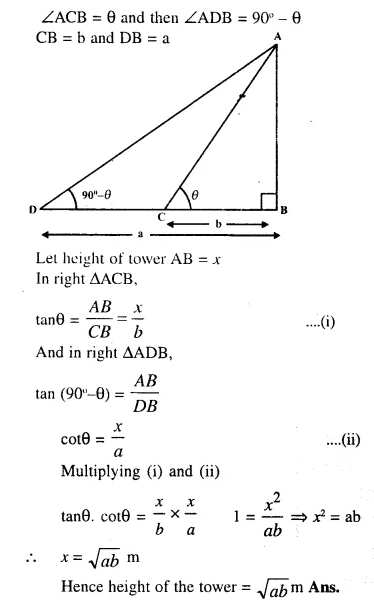
Question 10.
From a window A. 10 m above the ground the angle of elevation of the top C of a tower is x°, where tan x = 
Answer 10
Let CD be the height of the tower and height of window A from the ground = 10m
In right ∆AEC,
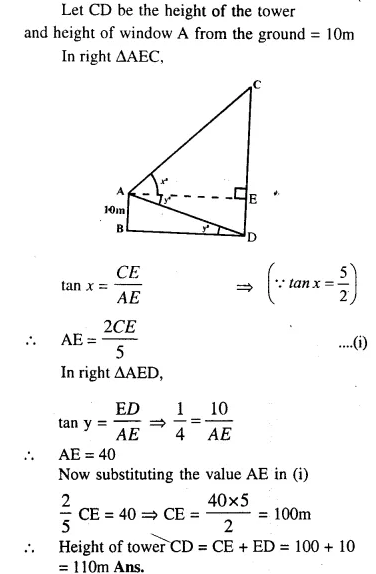
Question 11.
A vertical tower is 20 m high, A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower ? [2001]
Answer 11
Question 12.
A man standing on the bank of a river observes that the angle of elevation of a tree on the opposite bank is 60°. When he moves 50 m away from the bank, he finds the angle of elevation to be 30°. Calculate :
(i) the width of the river and
(ii) the height of the tree.
Answer 12
Let TR be the tree of height x m and y be the width AR of the river,
then ∠B = 30° and A = ∠60° , AB = 50 m.
Now in right ∆ATR,
Question 13.
A 20 m high vertical pole and a vertical tower are on the same level ground in such a way that the angle of elevation of the top of the tower, as seen from the foot of the pole, is 60° and the angle of elevation of the top of the pole as seen from the foot of the tower is 30°. Find
(i) the height of the tower.
(ii) the horizontal distance between the pole and the tower.
Answer 13
Let PQ is the pole and TS is the tower. PQ = 20 m.
Let TS = h and QS = x Angles of elevation from Q to T A T is 60° and from S to P is 30°.
In the ∆PQS
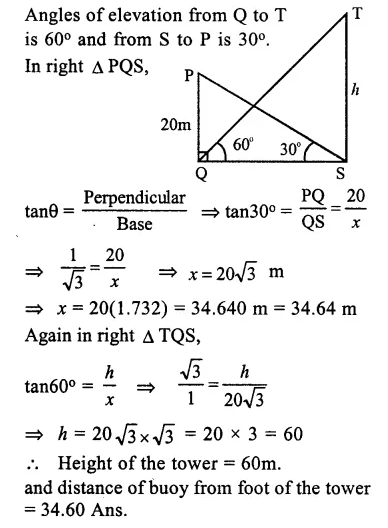
Question 14.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole the angle of elevation of the top of the tower is 60° and the angle of depression of the bottom of the tower is 30°.
Find : (i) the height of the tower, if the height of the pole is 20m;
(ii) the height of the pole, if the height of the tower is 75 m.
Answer 14
Let PQ is the pole and TW is the tower
Angle of elevation from T to P is 60° and angle of depression from P to W is 30°
∴ ∠PWQ = 30° = ∠RPW ( ∠ Altanate angles)
(i) In first case when height of pole OQ = 20m, Then in right ∆ PQW
Question 15.
From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
Answer 15
Let AQ is the sea-level
P is a point 36 m above sea-level
∴ PQ = 36
Let B be the bird and R is its reflection in the water and angle of elevation of the bird B at P is 30° and angle of depression of the reflection of the bird at R is 60°
Question 16.
……….
Answer 16
Question 17.
As observed from the top of a 80 m tall lighthouse, the angles of depression of two ships, on the same side of the light house in horizontal line with its base , are 30° and 40° respectively . Find the distance between the two ships.Give your answer correct to the nearest meter. [2012]
Answer 17
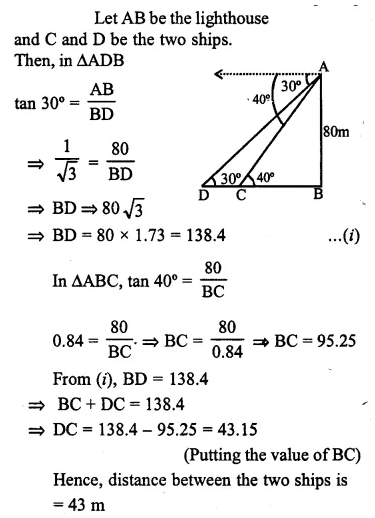
Question 18.
In the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find :
(i) the horizontal distance between AB and CD.
(it) the height of the lamp post.
Answer 18
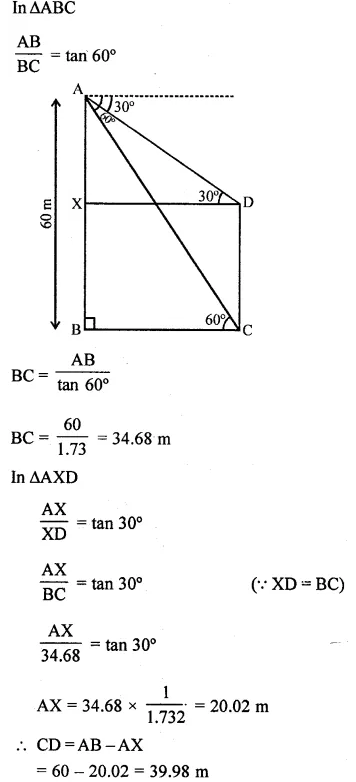
Question 19.
An aeroplane at an altitude of 250 m observes the angle of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number. (2014)
Answer 19
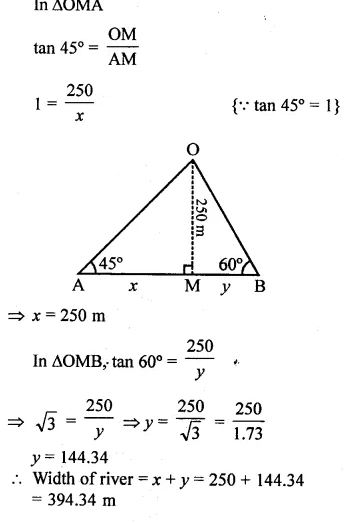
Question 20.
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second tower is 30° and 24° respectively. Find the height of the two towers. Give your answer correct to 3 significant figures. (2015)
Answer 20
AB and CD are two towers which are 120 m apart
i.e. BD= 120m
Angles of elevation of the top and angle of depression of bottom of the first tower observed from the top of second tower is 30° and 24°.
Question 21
The angles of depression of two ships A and B as observed from the top of a light house 60m high, are 60° and 45° respectively. If the two ships are on the opposite sides of the light house, find the distance between the two ships. Give your answer correct to the nearest whole number.
Answer 21
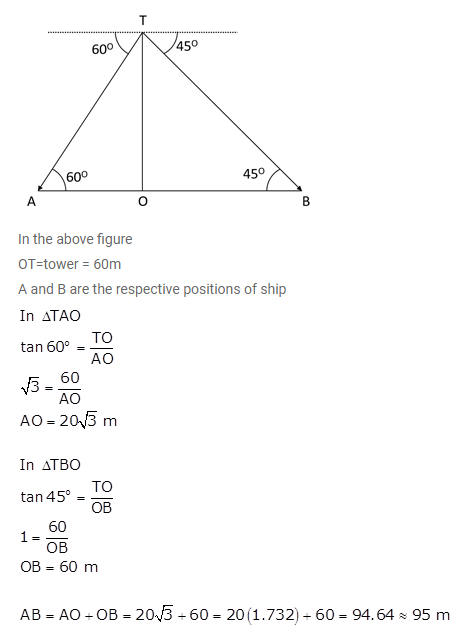
-: End of Height and Distances Chapter-22 Concise Solutions :-
Return to :- Concise Selina Maths Solutions for ICSE Class-10
Thanks
Please share with your friends
