ML Aggarwal Heights and Distances Exe-20 Solutions ICSE Class-10 Maths Ch-20. We Provide Step by Step Answer of Exercise-20 Heights and Distances Questions for ICSE Class-10 APC Understanding Mathematics. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Heights and Distances Exe-20 Solutions ICSE Class-10 Maths Ch-20
| Board | ICSE |
| Subject | Maths |
| Class | 10th |
| Chapter-20 | Heights and Distances |
| Writer / Book | Understanding |
| Topics | Solutions of Exe-20 |
| Academic Session | 2024-2025 |
ML Aggarwal Heights and Distances Exe-20 Solutions
ICSE Class-10 Maths Ch-20
Question 1. An electric pole is 10 metres high. If its shadow is 10√3 metres in length, find the elevation of the sun.
Answer :
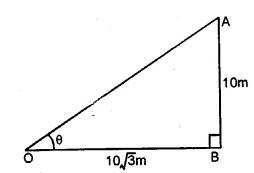
Let AB be the pole and
OB is its shadow.
AB = 10 m, OB = 10√3 m and θ is the angle of elevation of the sun.
We know that
tan θ = AB/ OB
tan θ = 10/10√3 = 1/√3
tan 300 = 1/√3
θ = 300
Question 2. The angle of elevation of the top of a tower from a point on the ground and at a distance of 150 m from its foot is 30°. Find the height of the tower correct to one place of decimal
Answer :
Let BC be the tower and
A is the point on the ground such that
∠A= 30° and AC = 150 m
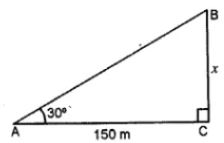
tan θ = BC/AC
tan 30° = x/150
By cross multiplication
1/√3 = x/150
So we get
x = 150/√3
Multiplying and dividing by √3
x = (150 ×√3)/(√3×√3)
By further calculation
x = 150√3/3 = 50√3 m
x = 50 (1.732)
⇒ x = 86.600 m
⇒ x = 86.6 m
(ML Aggarwal Heights and Distances Exe-20 Solutions)
Question 3. A ladder is placed against a wall such that it just reaches the top of the wall. The foot of the ladder is 1.5 metres away from the wall and the ladder is inclined at an angle of 60° with the ground. Find the height of the wall.
Answer :
Let AB be the wall and AC be the ladder
whose foot C is 1.5 m away from B
Let AB = x m and angle of inclination is 60°
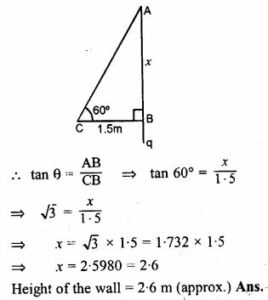
ML Aggarwal Heights and Distances Exe-20 Solutions
ICSE Class-10 Maths Ch-20
Page-478
Question 4. What is the angle of elevation of the sun when the length of the shadow of a vertical pole is equal to its height.
Answer :
Let AB be the pole and CB be its shadow
and θ is the angle of elevation of the sun.
Let AB = x m, then BC = x m
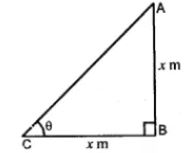
tan θ = AB/CB = x/x = 1
tan 45° = 1
⇒ θ = 45°
Hence, the angle of elevation of the sun is 45°.
Question 5. From a point P on level ground, the angle of elevation of the top of a tower is 30°. If the tower is 100 m high, how far is P from the foot of the tower ?
Answer :
Let AB be the tower and P is at a distance of x m from B, the foot of the tower.
While the height of the tower AB = 100 m
and angle of elevation = 30°
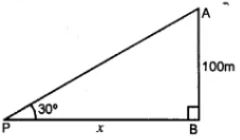
tan θ = AB/PB
tan 30° = 100/x
So we get
1/√3 = 100/x
By cross multiplication
x = 100√3
⇒ x = 100 (1.732) = 173.2 m
Question 6. From the top of a cliff 92 m high, the angle of depression of a buoy is 20°. Calculate to the nearest metre, the distance of the buoy from the foot of the cliff. (2005)
Answer :
Let AB be cliff whose height is 92 m
and C is buoy making depression angle of 20°.
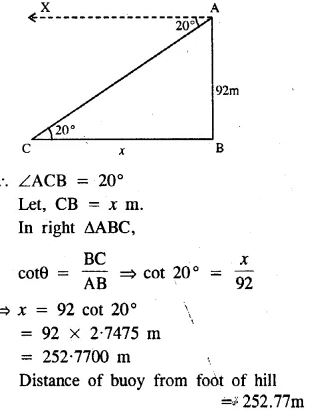
Question 7. A boy is flying a kite with a string of length 100 m. If the string is tight and the angle of elevation of the kite is 26°32′, find the height of the kite correct to one decimal place, (ignore the height of the boy).
Answer :
Let AB be the height of the kite A and AC is the string
and angle of elevation of the kite is 26°32′

Take AB = x m and AC = 100 m
sin θ = AB/AC
sin 26° 32’ = x/100
So we get
0.4467 = x/100
x = 100 × 0.4467
⇒ x = 44.67 = 44.7 m
Question 8. An electric pole is 10 m high A steel wire tied to the top of the pole is affixed at a point on the ground to keep the pole upright. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire.
Answer :
Let AB be the pole and AC be the wire
which makes an angle of 45° with the ground.
Height of the pole AB = 10 m
and let the length of wire AC = x m
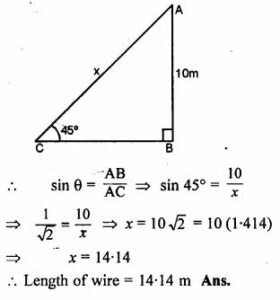
Question 9. A vertical tower is 20 m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower ? (2001)
Answer :
Let AB be the tower and
let a man C stands at a distance from the foot of the tower = x m
and cos θ = 0.53

Question 10. The upper part of a tree broken by wind, falls to the ground without being detached. The top of the broken part touches the ground at an angle of 38°30′ at a point 6 m from the foot of the tree. Calculate.
(i) the height at which the tree is broken.
(ii) the original height of the tree correct to two decimal places.
Answer :
Let TR be the total height of the tree
and TP is the broken part which touches the ground
at the distance of 6 m from the foot of the tree
making an angle of 38°30′ with the ground.
Let PR = x and TR = x + y
PQ = PT = y
In right ∆PQR
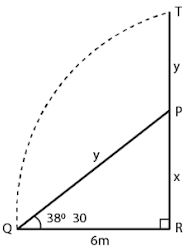
tan θ = PR/QR
tan 38° 30’ = x/6
x/6 = 0.7954
By cross multiplication
x = 0.7954 × 6 = 4.7724
We know that
sin θ = PR/PQ
sin 38° 30’ = x/y
So we get
0.6225 = 4.7724/y
⇒ y = 4.7724/0.6225 = 7.6665
Height of the tree = 4.7724 + 7.6665 = 12.4389 = 12.44 m
and height of the tree at which it is broken = 4.77 m
(ML Aggarwal Heights and Distances Exe-20 Solutions)
Question 11. An observer 1.5 m tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
Answer :
In the figure, AB is tower and CD is an observer.
θ is the angle of observation from
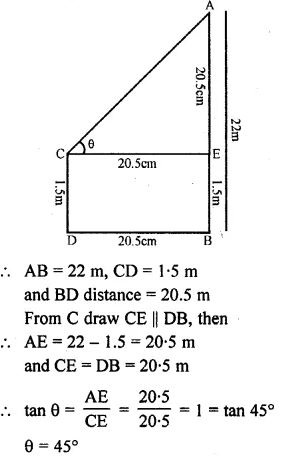
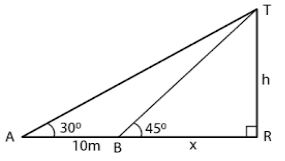
Question 12. In the adjoining figure, the angle of elevation from a point P of the top of a tower QR, 50 m high is 60° and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre.
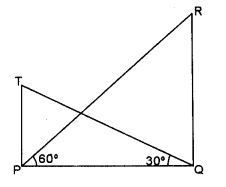
Answer :
Here, Height of the tower (QR) = 50 m
Height of the tower (PT) = h m
Inrt. ∠ed ∆ PQR, ∠RPQ = 60°

Hence, the required height of tower PT is 17 m (nearest to metre).
Question 13. From a point P on the ground, the angle of elevation of the top of a 10 m tall building and a helicopter hovering over the top of the building are 30° and 60° respectively. Find the height of the helicopter above the ground.
Answer :
let AB be the building and H is the helicopter hovering over it.
P is a point on the ground,
the angle of elevation of the top of building and helicopter are 30° and 60°
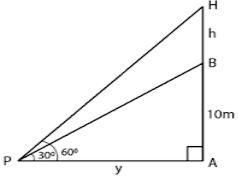
Height of the building AB = 10 m
Take PA = x m and BH = h m
In right triangle ABP
tan θ = P/B
tan 300 = AB/PA = 10/x
1/√3 = 10/x
⇒ x = 10√3 m
In right triangle APH
tan 600 = AH/PA
⇒ tan 600 = (10 + h)/ x
√3 = (10 + h)/ 10√3
10√3 × √3 = 10 + h
⇒ 30 = 10 + h
⇒ h = 30 – 10 = 20
Height of the helicopter from the ground = 10 + 20 = 30 m
Question 14. An aeroplane when flying at a height of 3125 m from the ground passes vertically below another plane at an instant when the angles of elevation of the two planes from the same point on the ground are 30° and 60° respectively. Find the distance between the two planes at the instant.
Answer :
Let the distance between the two planes = h m
Given that, AD = 3125 m and ∠ACB = 60° and ∠ACD = 30°
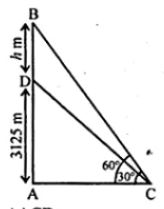
In triangle ACD
tan 300 = AD/AC
1/√3 = 3125/AC
⇒ AC = 3125√3 …(1)
In triangle ABC
tan 600 = AB/AC
√3 = (AD + DB)/ AC
So we get
√3 = (3125 + h)/ AC
⇒ AC = (3125 + h)/ √3 ….(2)
(3125 + h)/ √3 = 3125√3
h = (3125√3 × √3) – 3125
⇒ h = 3125 × 3 – 3125
⇒ h = 9375 – 3125
⇒ h = 6250 m
Therefore,
the distance between two planes at the instant is 6250 m.
Question 15. A man observes the angle of elevation of the top of the tower to be 45°. He walks towards it in a horizontal line through its base. On covering 20 m the angle of elevation changes to 60°. Find the height of the tower correct to 2 significant figures.
Answer :
Let AB be the tower of height h m. P and Q are the two observing points, such that
∠APB = 45°, ∠AQB = 60°, PQ = 20 m
In rt. ∠ed ∆QBA,
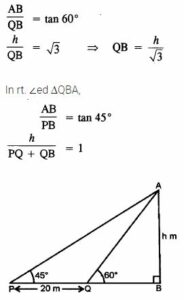
Hence, the height of the tower is 47.3 m.
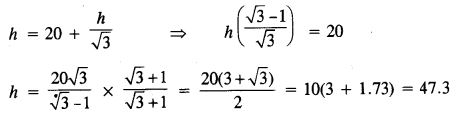
Question 16. The shadow of a vertical tower on a level ground increases by 10 m when the altitude of the sun changes from 45° to 30°. Find the height of the tower, correct to two decimal places. (2006)
Answer :
In the figure, AB is the tower,
BD and BC are the shadow of the tower in two situations.
Let BD = x m and AB = h m
tan 450 = h/x
1 = h/x
⇒ h = x …(1)
In triangle ABC
tan 300 = h/(x + 10)
1/√3 = h/(x + 10)
Using equation (1)
h√3 = h + 10
⇒ h (√3 – 1) = 10
h = 10/(√3 – 1)
h = [10 (√3 + 1)]/[(√3 – 1) (√3 + 1)]
h = (10√3 + 1)/ 2
h = 5 (1.73 + 1)
⇒ h = 5 × 2.73
⇒ h = 13.65 m
ML Aggarwal Heights and Distances Exe-20 Solutions
ICSE Class-10 Maths Ch-20
Page-479
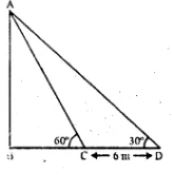
Question 17. From the top of a hill, the angles of depression of two consecutive kilometer stones, due east are found to be 30° and 45° respectively. Find the distance of two stones from the foot of the hill.
Answer :
Let A and B be the position of two consecutive kilometre stones.
Then AB = 1 km = 1000m
Let the distance BC = x m
∴ Distance AC = (1000 + x) m

Question 18. A man observes the angles of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m the angle of elevation changes to 60°. Find the height of the building correct to the nearest me he.
Answer :
Given that:
AB is a building CD = 60 m
In triangle ABC
tan 600 = AB/BC
√3 = AB/BC
BC = AB/√3 …(1)
In triangle ABD
tan 300 = AB/BD
⇒ 1/√3 = AB/(BC + 60)
BC + 60 = √3 AB
⇒ BC = √3 AB – 60
Using both the equations we get
AB/√3 = √3 AB – 60
AB = 3AB – 60√3
⇒ 3AB – AB = 60 × 1.732
AB = (60 × 1.732)/2
⇒ AB = 51.96 m
Question 19. At a point on level ground, the angle, of elevation of a vertical lower is found to be such that its tangent is 5/12. On walking 192 m towards the tower, the tangent of the angle is found to be  . Find the height of the tower. (1990)
. Find the height of the tower. (1990)
Answer :
Let TR be the tower and P is the point on the
ground such that tan θ = 5/12
tan α = ¾
PQ = 192 m
Take TR = x and QR = y
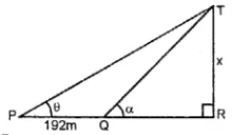
tan α = TR/QR = x\y
3/4 = x/y
⇒ y = 4/3 x …(1)
In right triangle TPR
tan θ = TR/PR
5/12 = x/(y + 192)
⇒ x = (y + 192) 5/12 …(2)
x = (4/3 x + 192) 5/12
So we get
x = 5/9 x + 80
⇒ x – 5/9 x = 80
⇒ 4/9 x = 80
x = (80 × 9)/4 = 180
(ML Aggarwal Heights and Distances Exe-20 Solutions)
Question 20. In the figure, not drawn to scale, TF is a tower. The elevation of T from A is x° where tan x =  and AF = 200 m. The elevation of T from B, where AB = 80 m, is y°. Calculate :
and AF = 200 m. The elevation of T from B, where AB = 80 m, is y°. Calculate :
(i) The height of the tower TF.
(ii) The angle y, correct to the nearest degree. (1997)
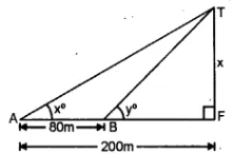
Answer :
Let height of the tower TF = x
tan x = 2/5, AF = 200 m, AB = 80 m
(i) In right ∆ATF,
tan x0 = TF/AF
2/5 = x/200
So we get
x = (2 × 200)/5
⇒ x = 400/5
⇒ x = 80 m
(ii) In right triangle TBF
tan y = TF/BF
tan y = 80/(200 – 80)
⇒ tan y = 80/120
⇒ tan y = 2/3 = 0.6667
y = 330 41’ = 340
Question 21. In the adjoining figure, not drawn to the scale, AB is a tower and two objects C and D are located on the ground, on the same side of AB. When observed from the top A of the tower, their angles of depression are 45° and 60°. Find the distance between the two objects. If the height of the tower is 300 m. Give your answer to the nearest metre.

Answer :
Let CB = x and
DB = y
AB = 300 m
tan θ = AB/CB
tan 450 = 300/x
⇒ 1 = 300/x
x = 300 m
In right triangle ADB
tan θ = AB/DB
tan 600 = 300/y
⇒ √3 = 300/y
y = 300/√3
Multiply and divide by √3
y = 300/√3 × √3/√3 = 300√3/3
So we get,
y = 100 × 1.732 = 173.2 m
CD = x – y = 300 – 173.2
= 126.8 = 127 m
Question 22. The horizontal distance between two towers is 140 m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 30°. If the height of the second tower is 60 m, find the height of the first tower.
Answer :
Let the height of first tower TR = x
height of second tower PQ = 60 m
Distance between the two towers QR = 140 m
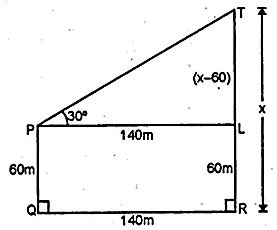
PL parallel to QR
LR = PQ = 60 m
PL = QR = 140 m
TL = (x – 60) m
In right triangle TPL
tan θ = TL/PL
tan 300 = (x – 60)/140
1/√3 = (x – 60)/140
x – 60 = 140/√3
Multiply and divide by √3
x – 60 = 140/√3 × √3/√3 = 140√3/3
x = 140√3/3 + 60
⇒ x = (140 × 1.732)/ 3 + 60
⇒ x = 80.83 + 60
⇒ x = 140.83
Question 23. As observed from the top of a 80 m tall lighthouse, the angles of depression of two ships on the same side of the , lighthouse in horizontal line with its base are 30° and 40° respectively. Find the distance between the two ships. Give your answer correct to the nearest metre.
Answer :
Let AB be the lighthouse and C and D be the two ships.
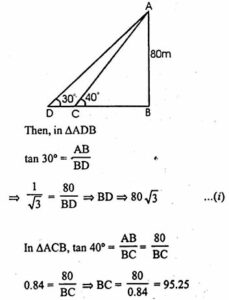
Using equation (1)
BD = 80 √3 = 80 × 1.73 = 138.4
Here we get
DC = BD – BC
⇒ DC = 138.4 – 95.25 = 43.15
Question 24. The angle of elevation of a pillar from a point A on the ground is 45° and from a point B diametrically opposite to A and on the other side of the pillar is 60°. Find the height of the pillar, given that the distance between A and B is 15 m.
Answer :
Let CD be the pillar and let CD = x
Angles of elevation of points A and B are 45° and 60° respectively.

Hence, the height of the pillar is 9.51 m.
Question 25. From two points A and B on the same side of a building, the angles of elevation of the top of the building are 30° and 60° respectively. If the height of the building is 10 m, find the distance between A and B correct to two decimal places
Answer :
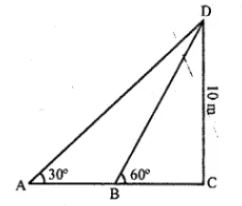
In triangle DBC
tan 600 = 10/BC
√3 = 10/BC
BC = 10/√3
In triangle DBC
tan 300 = 10/(BC + AB)
1/√3 = 10/[10/√3 + AB]
1/√3 [10/√3 + AB] = 10
AB = 10√3 – 10/√3
Taking LCM
AB = (30 – 10)/ √3
⇒ AB = 20/√3
⇒ AB = 20√3/3
AB = (20 × 1.732)/3
⇒ AB = 20 × 0.577
⇒ AB = 11.540 m
Question 26. The angles of depression of two ships A and B as observed from the top of a light house 60 m high are 60° and 45° respectively. If the; two ships are on the opposite sides of the light house, find the distance between the two ships. Give your answer correct to the nearest whole number. (2017)
Answer :
Let AD be the height of the lighthouse CD = 60 m
Let AD = x m, BD = y m
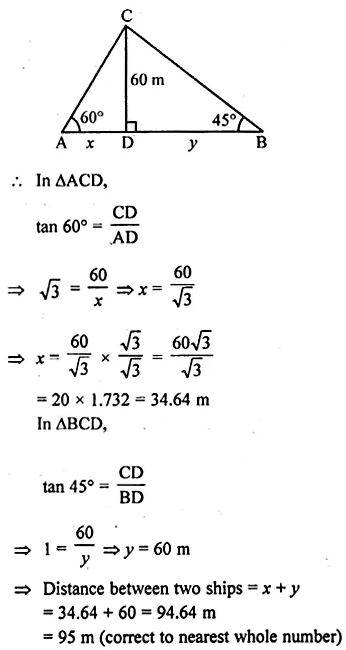
(ML Aggarwal Heights and Distances Exe-20 Solutions)
Question 27. An aeroplane at an altitude of 250 m observes the angle of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
Answer :
Let AD = 250 m height of aeroplane.
Two boats are at B and C.
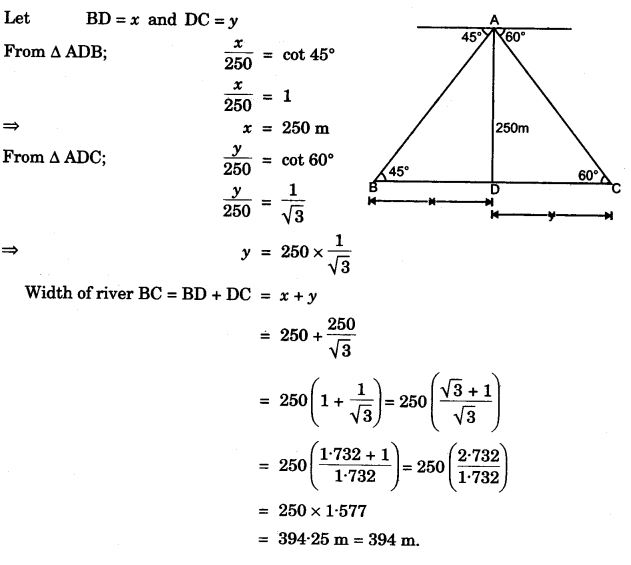
Question 28. From a tower 126 m high, the angles of depression of two rocks which are in a horizontal line through the base of the tower are 16° and 12°20′ Find the distance between the rocks if they are on
(i) the same side of the tower
(ii) the opposite sides of the tower.
Answer :
Let CD be the tower and CD = 126 m
Let A and B be the two rocks on the same line
and angles of depression are 16° and 12°20′ respectively,
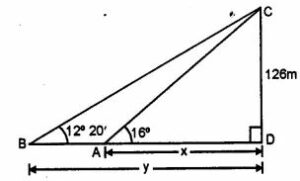
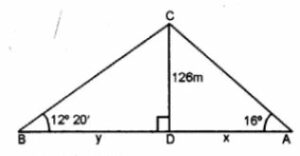
In triangle CAD
tan θ = CD/AD
tan 160 = 126/x
⇒ 0.2867 = 126/x
x = 126/0.2867
⇒ x = 439.48
In right triangle CBD
tan 120 20’ = 126/y
0.2186 = 126/y
⇒ y = 126/0.2186 = 576.40
(i) In the first case
On the same side of the tower
AB = BD – AD
⇒ AB = y – x
AB = 576.40 – 439.48
⇒ AB = 136.92 m
(ii) In the second case
On the opposite side of the tower
AB = BD + AD
⇒ AB = y + x
AB = 576.40 + 439.48
⇒ AB = 1015.88m
ML Aggarwal Heights and Distances Exe-20 Solutions
ICSE Class-10 Maths Ch-20
Page-480
Question 29. A man 1.8 m high stands at a distance of 3.6 m from a lamp post and casts a shadow of 5.4 m on the ground. Find the height of the lamp post.
Answer :
AB is the lamp post CD is the height of man.
BD is the distance of man from the foot of the lamp
and FD is the shadow of man.
CE || DB.
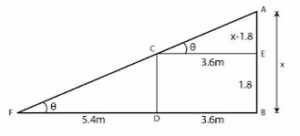
Take AB = x and CD = 1.8 m
EB = CD = 1.8 m
AE = x – 1.8
Shadow FD = 5.4 m
In right triangle ACE
tan θ = AE/CE
tan θ = (x – 1.8)/3.6 …(1)
In right triangle CFD
tan θ = CD/FD
tan θ = 1.8/5.4 = 1/3 …(2)
(x – 1.8)/3.6 = 1/3
3x – 5.4 = 3.6
⇒ 3x = 3.6 + 5.4 = 9.0
x = 9/3 = 3.0
Question 30. The angles of depression of the top and the bottom of an 8 m tall building from the top of a multi – storeyed building are 30° and 45° respectively. Find the height of tire multi-storeyed building and the distance between the two buildings, correct to two decimal places.
Answer :
Let AB be the CD be the building
The angles of depression in from A, to C
and D are 30° and 45° respectively
∠ACE = 30° and ∠ADB = 45°
CD = 8 m
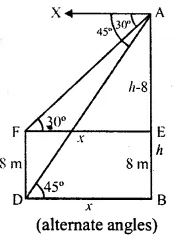
In right triangle ADB
tan θ = AB/DB
tan 450 = h/x
1 = h/x
⇒ x = h
In right triangle ACE
tan 300 = AE/CE
1/√3 = (h – 8)/h
h = √3h – 8√3
√3h – h = 8√3
⇒ h (√3 – 1) = 8√3
⇒ h = 8√3/(√3 – 1)
Multiply and divide by √3 + 1
h = 8√3/ (√3 – 1) × (√3 + 1)/(√3 + 1)
⇒ h = 8 (3 + √3)/(3 – 1)
Here
h = 8 (3 + 1.732)/2
⇒ h = 4 × 4.732
⇒ h = 18.928
⇒ h = 18.93 m
⇒ x = h = 18.93 m
Height of multi-storeyed building = 18.93 m
Question 31. A pole of height 5 m is fixed on the top of a tower. The angle of elevation of the top of the pole as observed from a point A on the ground is 60° and the angle of depression of the point A from the top of the tower is 45°. Find the height of the tower. (Take √3 = 1.732).
Answer :
Let QR be the tower and PQ be the pole on it
Angle of elevation from P to a point A is ∠PAR = 60°
and angle of depression from Q to A = 45°
∠QAR = 45° (alternate angle)
PQ = 5 m,
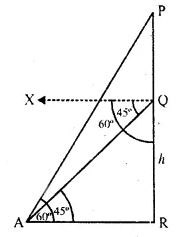
In right triangle QAR
tan θ = QR/AR
Substituting the values
tan 450 = h/AR
So we get
1 = h/AR
⇒ AR = h
In right triangle PAR
tan 600 = PR/AR
Substituting the values
√3 = (5 + h)/ h
So we get
√3h = 5 + h
⇒ h (√3 – 1) = 5
⇒ h (1.732 – 1) = 5
By further calculation
0.732 h = 5
⇒ h = 5/0.732 = 5000/732
⇒ h = 6.83
Question 32. A vertical pole and a vertical tower are on the same level ground. From the top of the pole the angle of elevation of the top of the tower is 60° and the angle of depression of the foot of the tower is 30°. Find the height of the tower if the height of the pole is 20 m.
Answer :
Let TR is tower and
PL is the pole on the same level, ground PL = 20m
From P, draw PQ || LR
then ∠ TPQ = 60° and ∠ QPR = 30°
∠PRL = ∠QPR = 300 which are the alternate angles
Take LR = x and TR = h
TQ = TR – QR = (h – 20) m

In right triangle PRL
tan θ = PL/LR
tan 300 = 20/x
1/√3 = 20/x
⇒ x = 20√3 m
In right triangle PQT
tan 600 = TQ/PQ
√3 = (h – 20)/x
⇒ √3 = (h – 20)/20√3
20√3 × √3 = h – 20
⇒ 20 × 3 = h – 20
⇒ h = 60 + 20 = 80 m
Question 33. From the top of a building 20 m high, the angle of elevation of the top of a monument is 45° and the angle of depression of its foot is 15°. Find the height of the monument.
Answer :
Let AB be the building and AB = 20 m and
let CD be the monument and let CD = x
The distance between the building and the monument be y,
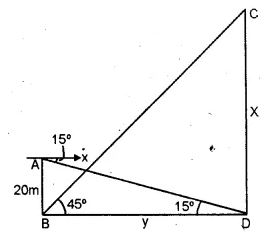
In right triangle BCD
tan θ = CD/BD
tan 450 = x/y
⇒ 1 = x/y
⇒ x = y …(1)
In right triangle ABD
tan 150 = AB/BD = 20/x
0.2679 = 20/x
x = 20/0.2679 = 74.65 m
(ML Aggarwal Heights and Distances Exe-20 Solutions)
Question 34. In the adjoining figure, the shadow of a vertical tower on the level ground increases by 10 m, when the altitude of the sun changes from 45° to 30°. Find the height of the tower and give your answer, correct to 1/10 of a metre.
Answer :
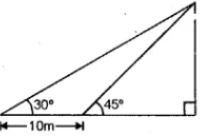
Let TR be the tower and TR = h ;
Let BR = x,
AB = 10 m
Angles of elevation from the top of the tower
at A and B are 30° and 45° respectively.

⇒ 0.732 h = 10
⇒ h = 10/0.732 = 13.66
Hence,
the height of the tower is 13.7 m.
Question 35. An aircraft is flying at a constant height with a speed of 360 km/h. From a point on the ground, the angle of elevation of the aircraft at an instant was observed to be 45°. After 20 seconds, the angle of elevation was observed to be 30°. Determine the height at which the aircraft is flying (use √3 = 1.732)
Answer :
Speed of aircraft = 360 km/h
Distance covered in 20 seconds = 360×20)/(60×60 = 2 km
E is the fixed point on the ground
and CD is the position of AB in height of aircraft
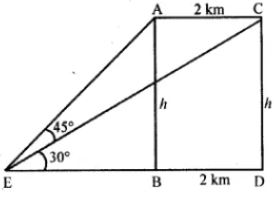
Take AB = CD = h km
In right triangle ARB
tan θ = AB/EB
tan 450 = h/EB
⇒ 1 = h/EB
⇒ EB = h
Here
ED = EB + BD = h + 2 km
In right triangle CED
tan 300 = CD/ED
1/√3 = h/(h + 2)
⇒ √3h = h + 2
⇒ 1.732h – h = 2
⇒ 0.732h = 2
2km = 2000 m
h = 2000/0.732
h = (2000 × 1000)/732
= 2732 m
— : End of ML Aggarwal Heights and Distances Exe-20 Solutions ICSE Class-10 Maths Ch-20 : –
Return to :- ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends


