ICSE Mathematics 2021 Specimen Paper for Class-10 Solved based on Further reduced syllabus. Specimen Mathematics ICSE Class-10 Paper for 2021. Model Specimen Paper for ICSE Board Class-10 Mathematics. Hence by better practice and Model Sample Paper ICSE Mathematics 2021 Specimen is very helpful for ICSE student appearing in 2020 exam of council. Visit official website www.cise.org for detail information about ICSE Class-10 Mathematics.
ICSE Mathematics 2021 Specimen Paper for Class-10 Solved
based on Further reduced syllabus
ICSE Mathematics 2021 Specimen Paper for Class-10 Solved
(Two hours and a half)
- Answers to this Paper must be written on the paper provided separately.
- You will not be allowed to write during the first 15 minutes.This time is to be spent in reading the question paper.
- The time given at the head of this Paper is the time allowed for writing the answers.
- Attempt all questions from Section A and any four questions from Section B.
- All working, including rough work, must be clearly shown and must be done on the same sheet as the part of the answer.
- Omission of essential working will result in loss of marks.
- The intended marks for questions or parts of questions are given in brackets [ ].
Mathematical tables are provided.
SECTION A (40 Marks)
ICSE Mathematics 2021 Specimen Paper for Class-10 Solved
Attempt all questions from this Section.
Question- 1
(a) Sonia had a recurring deposit account in a bank and deposited Rs. 600 per month for 2 ½ years. If the rate of interest was 10% p.a., find the maturity value of this account
(b )
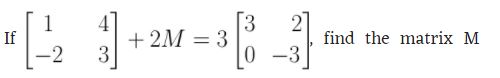
(c)
The marked price of an article is 12500. A dealer in Kolkata sells the article to consumer in the same city at a profit of 8%. If the rate of GST is 18%, find
(i) the selling price (excluding tax) of the article
(ii) IGST, CGST and SGST paid by the dealer to the Central and State Government
(iii) the amount which the consumer pays for the article.
Question- 2
(a) The area of the curved surface of a cylinder is 4400 cm2, and the circumference of its base is 110 cm. Find
(i) the height of the cylinder.
(ii) the volume of the cylinder.
(b)
A cone of maximum volume is curved out of a block of wood of size 20 cm x 10 cm x 10 cm. Find the volume of the remaining wood.
(c)
A bag contains 5 black, 7 red and 3 white balls. A ball is drawn at random from the bag, find the probability that the ball drawn is:
(i) red
(ii) black or white
(iii) not black.
Question- 3
(a )Express the ratios cos A, tan A and sec A in terms of sin A.
(b) A die is thrown once. What is the probability that the
(i) number is even
(ii) number is greater than 2 ?
Question-4
(a)
A river is 60 m wide. A tree of unknown height is on one bank. The angle of elevation of the top of the tree from the point exactly opposite to the foot of the tree on the other bank is 30°. Find the height of the tree.
(b)
Find the co-ordinates of the mid-point of the line segments joining the following pairs of points:
(i) (2, – 3), ( – 6, 7)
(ii) (5, – 11), (4, 3)
(iii) (a + 3, 5b), (2a – 1, 3b + 4)
SECTION B (40 Marks)
Attempt any four questions from this Section
Question- 5
(a) In the figure (i) given below, AB is a diameter of the circle APBR. APQ and RBQ are straight lines, ∠A = 35°, ∠Q = 25°. Find (i) ∠PRB (ii) ∠PBR (iii) ∠BPR.
(b) In the figure (ii) given below, it is given that ∠ABC = 40° and AD is a diameter of the circle. Calculate ∠DAC.
Question- 6
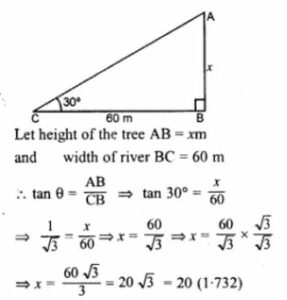
(a)
In the adjoining figure, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2 and DP produced meets AB produced at Q. If area of ∆CPQ = 20 cm², find

(i) area of ∆BPQ.
(ii) area ∆CDP.
(iii) area of || gm ABCD.
(b)
On a map drawn to a scale of 1 : 25000, a rectangular plot of land, ABCD has the following measurements AB = 12 cm and BG = 16 cm.
Calculate:
(i) the distance of a diagonal of the plot in km.
(ii) the area of the plot in sq. km.
Question- 7
(a)
Marks obtained by 40 students in a short assessment are given below, where a and b are two missing data.

If the mean of the distribution is 7.2, find a and b.
(b)
From the following frequency distribution, find :
(i) the median
(ii) lower quartile
(iii) upper quartile
(iv) inter quartile range

Question- 8
(a)
If point A is reflected in the y-axis, the co-ordinates of its image A1, are (4, – 3),
(i) Find the co-ordinates of A
(ii) Find the co-ordinates of A2, A3 the images of the points A, A1, Respectively under reflection in the line x = – 2
(b)
If point A is reflected in the y-axis, the co-ordinates of its image A1, are (4, – 3),
(i) Find the co-ordinates of A
(ii) Find the co-ordinates of A2, A3 the images of the points A, A1, Respectively under reflection in the line x = – 2
Question- 9
(a) The difference between the squares of two numbers is 45. The square of the smaller number is 4 times the larger number. Determine the numbers.
(b) From a pack of 52 cards, a blackjack, a red queen and two black kings fell down. A card was then drawn from the remaining pack at random. Find the probability that the card drawn is
(i) a black card
(ii) a king
(iii) a red queen.
Question- 10
(a)
Show that (x – 2) is a factor of 3x2 – x – 10. Hence factorise 3x2 – x – 10.
(b)
If P is the solution set of – 3x + 4 < 2x – 3, x ∈ N and Q is the solution set of 4x – 5 < 12, x ∈ W, find
(i) P ∩ Q
(ii) Q – P.
Solutions of ICSE Maths Specimen Paper -2021
Ans-1
(a)
Principal (n)= 2.5 year= 2.5*12 month=30 months
Principal (P)= Rs 600
Rate = 10% p.a.
Maturity Value= ……………
S.I.= P*n(n+1)*r*1/(2*100*12)
” ” = 600*30*31/2*100*12
Simple Interest .= RS 2335
Now Maturity Value = P*n+S.I.
Maturity Value=600*30+2325
…………………=RS 20325 Ans
(b)
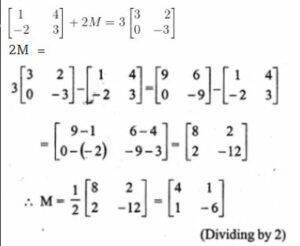
(c)
(i) the selling price (excluding tax) of the article
12500 + 12500 x 8/100
12500 + 1000
13500
(ii) IGST, CGST and SGST paid by the dealer to the Central and State Government
IGST, is nil due to intra state
CGST paid by the dealer to the Central Government
13500 x 9/100
1215
SGST paid by the dealer to the State Government
13500 x 9/100
1215
(iii) the amount which the consumer pays for the article.
Amount = Selling price + CGST + SGST
13500 + 1215 +1215
15930
Ans-2
(a)
Area of the curved surface of a cylinder = 4400 cm2
Circumference of base = 110 cm

(b)
Size of wooden block = 20 cm × 10 cm × 10 cm
Maximum diameter of the cone = 10 cm
and height (h) = 20 cm

(c)
In a bag,
Number of black balls = 5
and Number of red balls = 7
while number of white balls = 3
Total number of balls in the bag
= 5 + 7 + 3 = 15
(i) Probability of red balls

Ans-3
(a)

(b)
Dice is thrown once
Sample space = {1, 2, 3, 4, 5, 6}
(i) No. of ways in favour = 3
(∵ Even numbers are 2, 4, 6)
Total ways = 6
Probability = 6⁄3 = 1⁄2
(ii) No. of ways in favour = 4
(Numbers greater than 2 are 3, 4, 5, 6)
Total ways = 6
Probability = 4⁄6 = 2⁄3
Ans-4
(a)
Let AB be the tree and BC is the width of the river
and C is the point exactly opposite to B on the other bank
and angle of elevation is 30°.
= 36.640 = 36.64 m
Height of tree= 36.64 m
(b)
(i) Co-ordinates of the mid-point of (2, -3), ( -6, 7)

Ans-5
(a)
(i) ∠PRB = ∠BAP
(Angles in the same segment of the circle)
∴ ∠PRB = 35° (∵ ∠BAP = 35° given)
(ii) In ∆PRQ,

Ans-6
(a)
In the figure, ABCD is a parallelogram.
P is a point on BC such that BP : PC = 1 : 2
and DP is produced to meet ABC produced at Q.
Area ∆CPQ = 20 cm²

(b)
Scale factor (k) = 1⁄2500
Measurements of plot ABCD on the map are
AB = 12 cm and BC = 16 cm.

Ans-7
(a)
2a+15-3a=14
a=1
similar a+b=5
1+b=5
b=4
Solving (i) and (ii)
get a=1 , b= 4
(b)
Writing frequency distribution in c.f. table :

Ans-8
(a)
(i) ∵ A is reflected in the y-axis and its image is A1 (4, -3)
Co-ordinates of A will be (-4, -3)


Ans-9
(a)
Let the larger number = x
then smaller number = y
Now according to the condition,

(b)
In a pack of 52 cards, a blackjack, a red queen, two black being felt down.
Then number of total out comes = 52 – (1 + 1 + 2) = 48
(i) Probability of a black card (which are 26 – 3 = 23) = 23⁄48
(ii) Probability of a being (4 – 2 = 2) = 2⁄48 = 1⁄24
(iii) Probability of a red queen = (2 – 1 = 1) = 1⁄18
Ans-10
(a)
Let x – 2 = 0, then x = 2
Substituting the value of x in f(x),

(b)
(i) – 3 x + 4 < 2 x – 3
– 3x – 2x < – 3 – 4 => – 5x < – 7

Thanks





information about the solution should be at the top of the page ..
thanks for your suggestion
we will sure solve it in its update version (2021-2022 session)
team icsehelp
yess. And nice thing is that SOLUTION ARE GIVEN AT END…not after each respective question as other Q. paper.
thanks
In Q.paper, There is the absence of questions from chapter TANGENT AND INTERSECTING CHORDS as well as ARITHMETIC PROGRESSION.
*Please look for it.
Also, thanks for making paper from reduced syllabus 🙂 !
pls look for the answer of Q.4(a), it’s answer is 34.64 m not 36.64 m.
“20*1.732”.
ok
ok