Inequalities Concise Class-9th Selina ICSE Maths Solution Chapter-11. We provide step by step Solutions of Exercise / lesson-11 Inequalities for ICSE Class-9 Concise Selina Mathematics by R K Bansal.
Our Solutions contain all type Questions with Exe-11 A to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-9 Mathematics .
Inequalities Concise Class-9th Selina ICSE Maths Solution Chapter-11
Exercise – 11
Question 1
From the following figure, prove that: AB > CD.
………………….
Answer

Question 2
In a triangle PQR; QR = PR and ∠P = 36o. Which is the largest side of the triangle?
Answer

Since ∠R is the greatest, therefore, PQ is the largest side.
Question 3
If two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b.
Answer
The sum of any two sides of the triangle is always greater than third side of the triangle.
Third side < 13+8 =21 cm.
The difference between any two sides of the triangle is always less than the third side of the triangle.
Third side > 13-8 =5 cm.
Therefore, the length of the third side is between 5 cm and 9 cm, respectively.
The value of a =5 cm and b= 21cm.
Question 4
In each of the following figures, write BC, AC and CD in ascending order of their lengths.
………………..
Answer

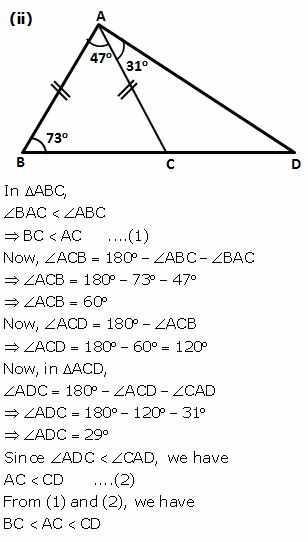
Question 5
Arrange the sides of ∆BOC in descending order of their lengths. BO and CO are bisectors of angles ABC and ACB respectively.
………………………
Answer
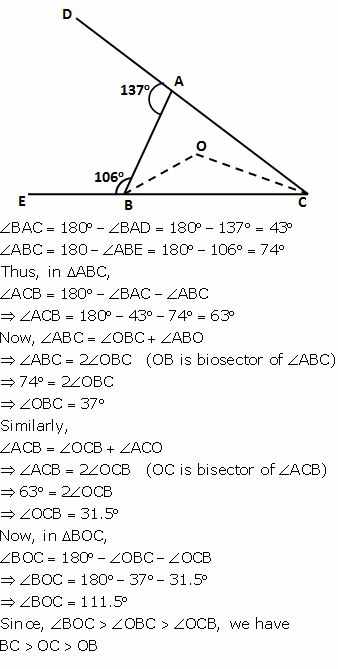
Question 6
D is a point in side BC of triangle ABC. If AD > AC, show that AB > AC.
Answer
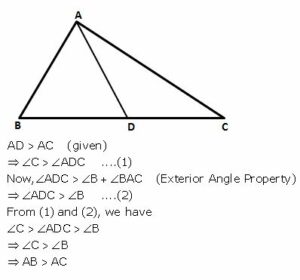
Question 7
n the following figure, ∠BAC = 60o and ∠ABC = 65o.
Prove that:
(i) CF > AF
(ii) DC > DF
Answer


Question 8
In the following figure; AC = CD; ∠BAD = 110o and ∠ACB = 74o.
Prove that: BC > CD
Answer


Question 9
From the following figure; prove that:
(i) AB > BD
(ii) AC > CD
(iii) AB + AC > BC
Answer

Question 10
In a quadrilateral ABCD; prove that:
(i) AB+ BC + CD > DA
(ii) AB + BC + CD + DA > 2AC
(iii) AB + BC + CD + DA > 2BD
Answer
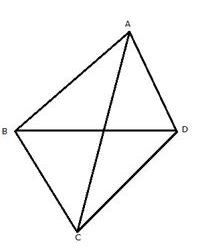
Const: Join AC and BD.
(i) In ΔABC,
AB + BC > AC….(i)[Sum of two sides is greater than the
third side]
In ΔACD,
AC + CD > DA….(ii)[ Sum of two sides is greater than the
third side]
Adding (i) and (ii)
AB + BC + AC + CD > AC + DA
AB + BC + CD > AC + DA – AC
AB + BC + CD > DA …….(iii)
(ii)In ΔACD,
CD + DA > AC….(iv)[Sum of two sides is greater than the
third side]
Adding (i) and (iv)
AB + BC + CD + DA > AC + AC
AB + BC + CD + DA > 2AC
(iii) In ΔABD,
AB + DA > BD….(v)[Sum of two sides is greater than the
third side]
In ΔBCD,
BC + CD > BD….(vi)[Sum of two sides is greater than the
third side]
Adding (v) and (vi)
AB + DA + BC + CD > BD + BD
AB + DA + BC + CD > 2BD
Question 11
In the following figure, ABC is an equilateral triangle and P is any point in AC; prove that:
(i) BP > PA
(ii) BP > PC
………………..
Answer

Question 12
P is any point inside the triangle ABC. Prove that:
∠BPC > ∠BAC.
Answer
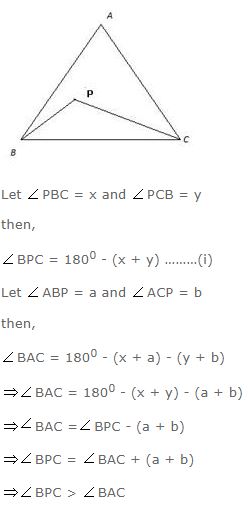
Question 13
Prove that the straight line joining the vertex of an isosceles triangle to any point in the base is smaller than either of the equal sides of the triangle.
Answer
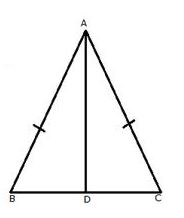
We know that exterior angle of a triangle is always greater than each of the interior opposite angles.
In ΔABD,
∠ADC > ∠B ……..(i)
In ABC,
AB = AC
∠B = ∠C …..(ii)
From (i) and (ii)
∠ADC > ∠ C
(i) In ΔADC,
∠ADC > ∠C
AC > AD ………(iii) [side opposite to greater angle is greater]
(ii) In ΔABC,
AB = AC
AB > AD[ From (iii)]
Question 14
In the following diagram; AD = AB and AE bisects angle A. Prove that:
(i) BE = DE
(ii) ∠ABD > ∠C
…………………
Answer


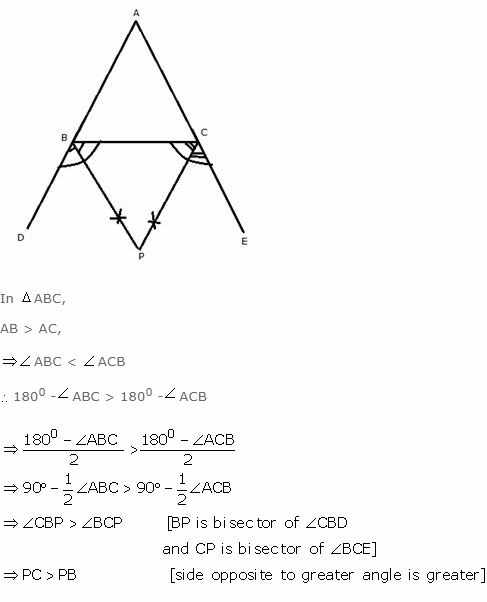
Question 15
The sides AB and AC of a triangle ABC are produced; and the bisectors of the external angles at B and C meet at P. Prove that if AB > AC, then PC > PB.
Answer
Question 16
In the following figure; AB is the largest side and BC is the smallest side of triangle ABC.
Write the angles xo, yo and zo in ascending order of their values.
Answer
Since AB is the largest side and BC is the smallest side of the triangle ABC
Since AB is the largest side and BC is the smallest side of the triangle ABC.
AB > AC > BC
⇒ 180° – z° > 180° – y° > 180° – x°
⇒ – z° > -y° > – x°
⇒ z° > y° > x°.
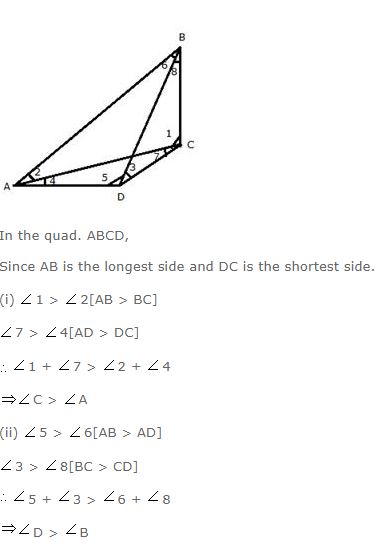
Question 17
In quadrilateral ABCD, side AB is the longest and side DC is the shortest.
Prove that:
(i) ……………
(ii)………..
Answer
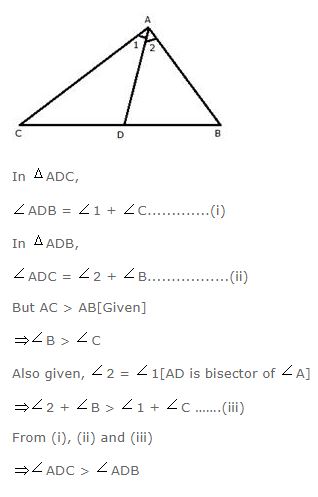
Question 18
In triangle ABC, side AC is greater than side AB. If the internal bisector of angle A meets the opposite side at point D, prove that: ∠ADC is greater than ∠ADB.
Answer
Question 19
In isosceles triangle ABC, sides AB and AC are equal. If point D lies in base BC and point E lies on BC produced (BC being produced through vertex C), prove that:
(i) AC > AD
(ii) AE > AC
(iii) AE > AD
Answer
We know that the bisector of the angle at the vertex of an isosceles triangle bisects the base at right angle.
Using Pythagoras theorem in AFB,
AB2 = AF2 + BF2…………..(i)
In AFD,
AD2 = AF2 + DF2…………..(ii)
We know ABC is isosceles triangle and AB = AC
AC2 = AF2 + BF2 ……..(iii)[ From (i)]
Subtracting (ii) from (iii)
AC2 – AD2 = AF2 + BF2 – AF2 – DF2
AC2 – AD2 = BF2 – DF2
Let 2DF = BF
AC2 – AD2 = (2DF)2 – DF2
or AC2 – AD2 = 4DF2 – DF2
AC2 = AD2 + 3DF2
hence AC2 > AD2
AC > AD
Similarly, AE > AC and AE > AD.
Question 20
Given: ED = EC
Prove: AB + AD > BC.
…………
Answer
The sum of any two sides of the triangle is always greater than the third side of the triangle.

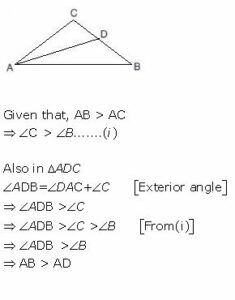
Question 21
In triangle ABC, AB > AC and D is a point in side BC. Show that: AB > AD.
Answer
— End of Inequalities Concise Class-9th Selina ICSE Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -9
Thanks


