ISC Mathematic 2021 Specimen Paper for Class-12 Solved

ISC Mathematic 2021 Specimen Paper for Class-12 Solved Question Paper for practice. Step by step Solutions with section-A, B and C. Visit official website CISCE for detail information about ISC Board Class-12 Maths.

By the practice of ISC Mathematic 2021 Specimen Paper for Class-12 Solved Question Paper you can get the idea of solving. Try Also other year except ISC Mathematic 2021 Specimen Paper for Class-12 Solved Question Paper of Previous Year for more practice. Because only  ISC Mathematic 2021 Specimen Paper for Class-12 is not enough for complete preparation of next council exam.

ISC Mathematic 2021 Specimen Paper for Class-12 Solved

---

-: Topics Included :-

Section-A

Section-B

Section-C

---

ISC Mathematic 2021 Specimen Paper for Class-12 Solved

Time Allowed: 3 Hours
Maximum Marks: 100

(Candidates are allowed additional 15 minutes for only reading the paper. They must NOT start writing during this time.)

• Candidates are required to attempt all questions from Section A and all questions either from Section B or Section C.
• Section A: Internal choice has been provided in three questions of four marks each and two questions of six marks each.
• Section B: Internal choice has been provided in two questions of four marks each.
• Section C: Internal choice has been provided in two questions of four marks each.
• All working, including rough work, should be done on the same sheet as, and adjacent to the rest of the answer.
• The intended marks for questions or parts of questions are given in brackets [ ].
• Mathematical tables and graph papers are provided.

---

Section – A (80 Marks)

ISC Mathematic 2021 Specimen Paper for Class-12

Question 1:

(i) If y – 2x – k = 0 touches the conic 3x² – 5y² = 15, find the value of k.

(ii) Prove that

(iii) Evaluate:

(iv)

(v) Without expanding at any stage, find the value of:

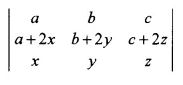
(vi) If A and B are events such that P(A) = ,1/2 P(B) = 1/3 and P(A∩B) = 1/4, then find: (a) P(A/B) (b) P(B/A)

(vii) Show that (A + A’) is symmetric matrix. if A =

(viii) Two balls are drawn from an urn containing 3 white, 5 red and 2 black balls, one by one without replacement. What is the probability that at least one ball is red?

(ix) If f: R → R, f(x) = x³ and g: R → R, g (x) = 2x² + 1, and R is the set of real numbers, then find fog(x) and gof (x).

(x) Find the matrix X for which:

Question 2:

(a) If

(b) Write the Boolean function corresponding to the switching circuit given below: [5]

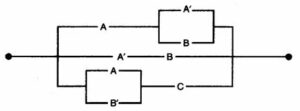
A, B and C represent switches in ‘on’ position and A’, B’ and C’ represent them in ‘off position. Using Boolean algebra, simplify the function and construct an equivalent switching circuit.

Question 3:

(a) Calculate Karl Pearson’s coefficient of correlation between x and y for the following data and interpret the result: [5]
(1, 6), (2, 5), (3, 7), (4, 9), (5, 8), (6, 10), (7, 11), (8, 13), (9, 12)
(b) The marks obtained by 10 candidates in English and Mathematics are given below: [5]
Estimate the probable score for Mathematics if the marks obtained in English are 24.

Question 4:

If tan^-1a + tan^-1b + tan^-1c = π, prove that a + b + c = abc.

Question 5:

Use properties of determinants to solve for x:

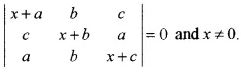
Question 6:

(a) Evaluate:
(b) Draw a rough sketch of the curve y² = 4x and find the area of region enclosed by the curve and the line y = x.

Question 7:

(a) Prove that locus of z is circle and find its centre and radius if (z – i)/(z – 1) is purely imaginary. [5]
(b) Solve: (x² – yx²) dy + (y² + xy²) dx = 0 [5]

Question 8:

Question 9:

Question 10:

Bag A contains 4 white balls and 3 black balls, while Bag B contains 3 white balls and 5 black balls. Two balls are drawn from Bag A and placed in Bag B. Then, what is the probability of drawing a white ball from Bag B?

Question 11:

Solve the following system of linear equations using matrix method:

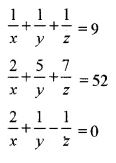
Question 12:

(a) Show that the function  is continuous at x = 1 but not differentiable.
Or
(b) Verify Rolle’s theorem for the following function:
f(x) = e^-x sin x on [0, π]

Question 13:

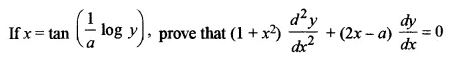
Question 14:

Evaluate: ∫ tan-1√x dx

---

Section – B (20 Marks)

Question 15:

A cone is inscribed in a sphere of radius 12 cm. If the volume of the cone is maximum, find its height.

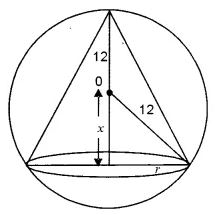
Question 16:

(a) Draw a rough sketch of the curve and find the area of the region bounded by curve y² = 8x and the line x = 2.
Or
(b) Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = -6 and x = 0.

Question 17:

(a) Find the equation of the plane passing through the intersection of the planes 2x + 2y – 3z – 7 = 0 and 2x + 5y + 3z – 9 = 0 such that the intercepts made by the resulting plane on the x – axis and the z – axis are equal.
Or
(b) Find the equation of the lines passing through the point (2, 1, 3) and perpendicular to the lines

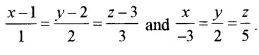
Question 18:

(a) In an automobile factory, certain parts are to be fixed into the chassis in a section before it moves into another section. On a given day, one of the three persons A, B and C carries out this task. A has a 45% chance, B has 35% chance and C has a 20% chance of doing the task. The probability that A, B and C will take more than the allotted time is 1/6, 1/10 and 1/20 respectively.
If it is found that the time taken is more than the allotted time, what is the probability that A has done the task?
(b) The difference between mean and variance of a binomial distribution is 1 and the difference of their squares is 11. Find the distribution.

---

Section – C (20 Marks)

ISC Mathematic 2021 Specimen Paper for Class-12

Question 19:

(a) A man borrows ₹ 20,000 at 12% per annum, compounded semi-annually and agrees to pay it in 10 equal semi-annual instalments. Find the value of each instalment, if the first payment is due at the end of two years.
(b) A company manufactures two types of products A and B. Each unit of A requires 3 grams of nickel and 1 gram of chromium, while each unit of B requires 1 gram of nickel and 2 grams of chromium. The firm can produce 9 grams of nickel and 8 grams of chromium. The profit is ₹ 40 on each unit of the product of type A and ₹ 50 on each unit of type B. How many units of each type should the company manufacture so as to earn a maximum profit? Use linear programming to find the solution.

Question 20:

(a) Given the total cost function for x units of a commodity as:
C(x) = 1/3 x³ + 3x² – 16x + 2.

Find:
(i) Marginal cost function
(ii) Average cost function
(b) Find the coefficient of correlation from the regression lines: x – 2y + 3 = 0 and 4x – 5y + 1 = 0.
(c) The average cost function associated with producing and marketing x units of an item is given by AC = 2x – 11 + 50/x. Find the range of values of the output x, for which AC is increasing.

Question 21:

A manufacturing company makes two types of teaching aids A and B of Mathematics for Class X. Each type of A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available per week are 180 and 30 respectively. The company makes a profit of ₹ 80 on each piece of type A and ₹ 120 on each piece of type B. How many pieces of type A and type B should be manufactured per week to get a maximum profit? Formulate this as Linear Programming Problem and solve it. Identify the feasible region from the rough sketch.

Question 22:

(a) The price relatives and weights of a set of commodities are given below: [5]

If the sum of the weights is 40 and the weighted average of price relatives index number is 122, find the numerical values of x and y.
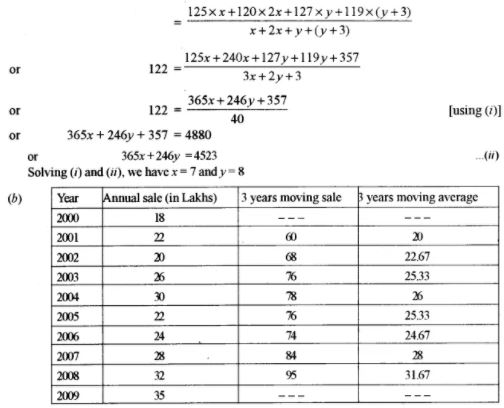
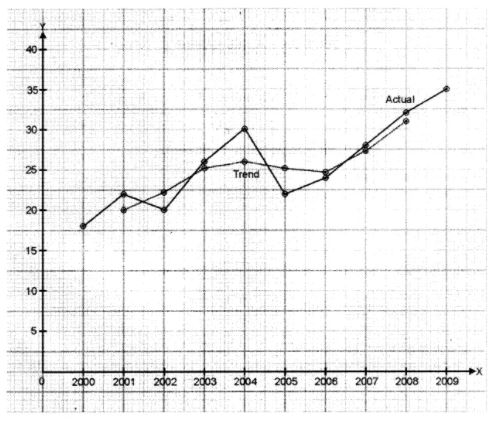
(b) Construct 3 yearly moving averages from the following data and show on a graph against the original data: [5]

---

Solution

Answer 1:

(i)

(ii)

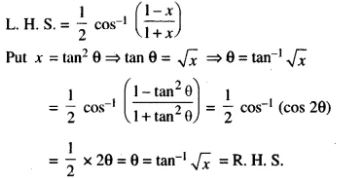
(iii)

(iv)

(v)

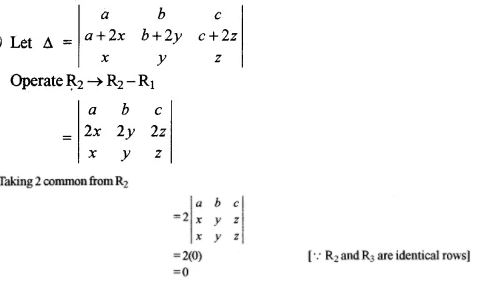
(vi)

(vii)

(viii)

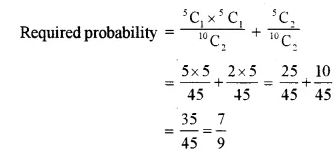
(ix)

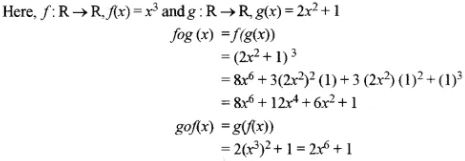
(x)

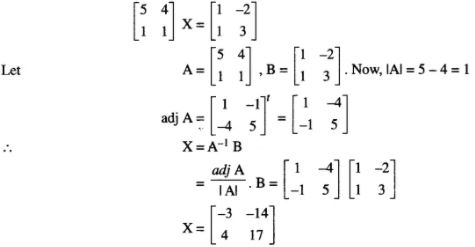
Answer 2:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

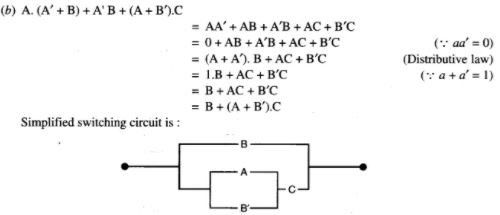
Answer 3:

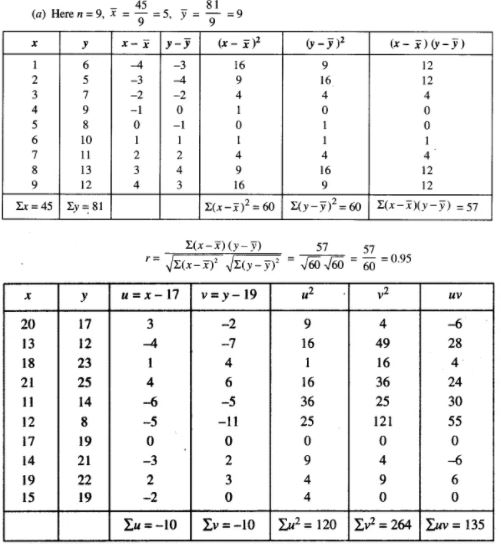
(b) Here n = 10.
Take the marks obtained in English and Mathematics as x and y respectively.
Let for x assumed mean be 17 and for v assumed mean be 19.
We construct the table as follows:

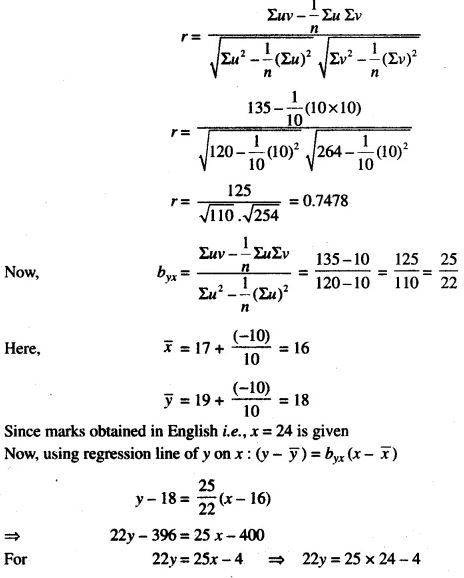
y = 596/22  = 27.09 = 27 marks approx.
Probable marks of mathematics is 27, when marks obtained in English are 24.

Answer 4:

Answer 5:

Answer 6:

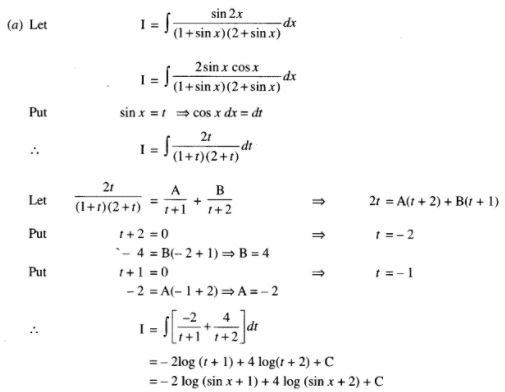
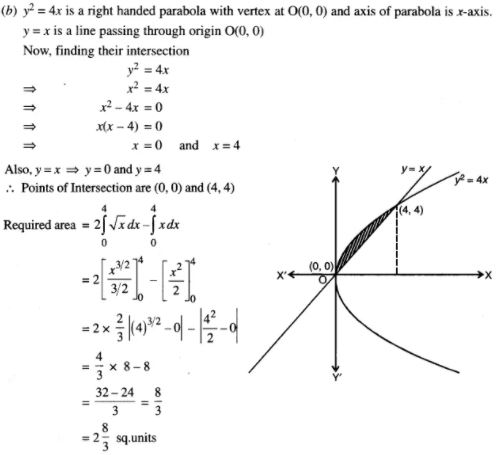
Answer 7:

Answer 8:

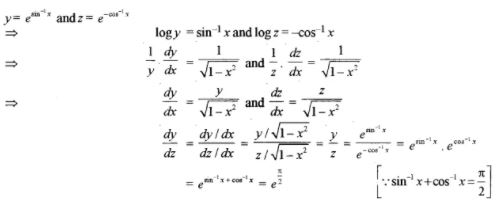
Answer 9:

Answer 10:

Here, we have three cases
Case 1: Two balls drawn from Bag A are White.
Case 2: Two balls drawn from Bag A are Black.
Case 3: Two balls drawn from Bag A are one White and other Black.

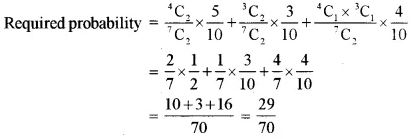
Answer 11:

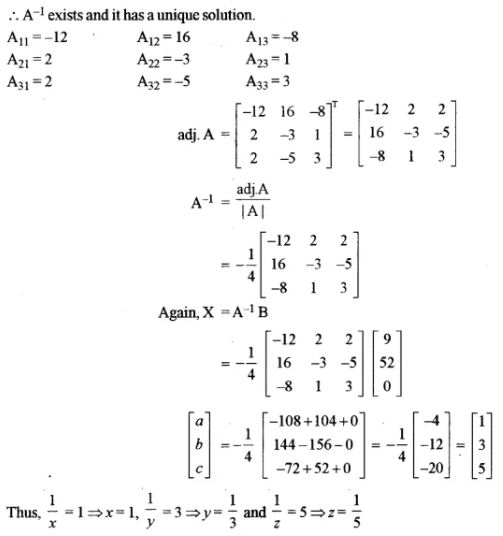
Answer 12:

Answer 13:

Answer 14:

---

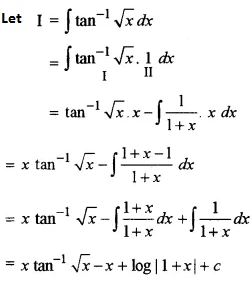
Answer 15:

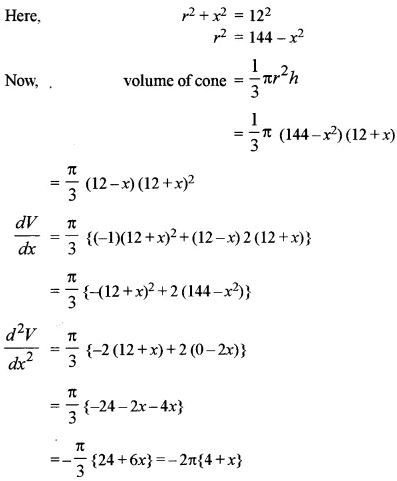
Answer 16:

(a) Given curves are:
y² = 8x …(i)
and x = 2 …(ii)
Putting x = 2 in eqn. (i),
we have y² = 16
⇒ y = ±4
when x = 2, y = 4
when x = 2, y = -4
Points of intersections are (2, 4) and (2, -4)

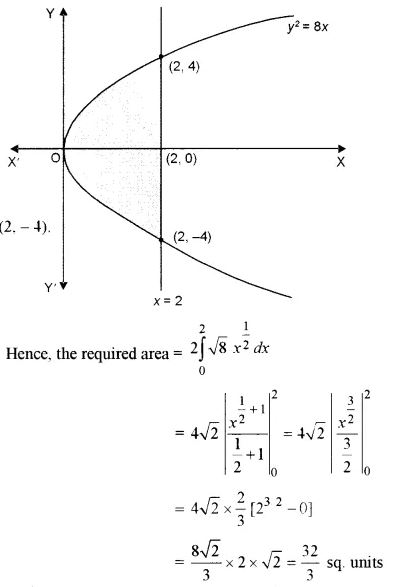
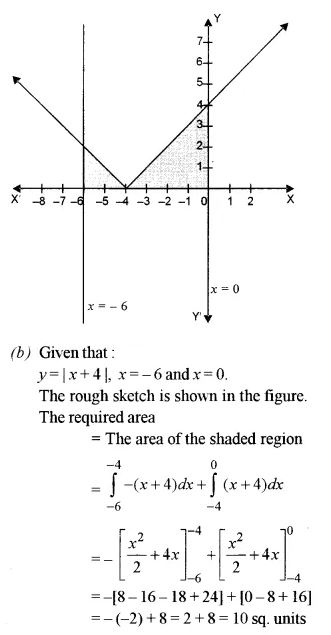
Answer 17:

(a) Given planes are:
2x + 2y – 3z – 7 = 0 … (i)
and 2x + 5y + 3z – 9 = 0 … (ii)
Equation of the plane passing through the intersection of the planes (i) and (ii) is:

Answer 18:

---

Answer 19:

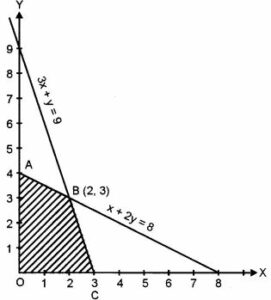
Coordinates of O is (0, 0)
Coordinates of A is (0, 4)
Coordinates of C is (3, 0)
Coordinates of B is (2, 3)
At O, Z = 0
At A, Z = 40 × 0 + 50 × 4 = ₹ 200
At B, Z = 40 × 2 + 50 × 3 = 80 + 150 = ₹ 230
At C, Z = 40 × 3 + 50 × 0 = ₹ 120
The feasible region is the shaded portion.
Maximum profit is ₹ 230 at B (2, 3) i.e., the company produces 2 units of type A product and 3 units of type B product

Answer 20:

(a) Given the total cost function for x units of a commodity is:
C(x) = 1/3 x³ + 3x² – 16x + 2
(i) C'(x) = x² + 6x – 16
Which is the required marginal cost function
(ii) Average cost function = c(x)/x
1/3 x + 3x – 16 + 2/x
(b) Given regression lines are:
x – 2y + 3 = 0 …..(i)
and 4x – 5y + 1 = 0 …..(ii)
From eqn. (i), we have
x = 2y – 3
Reg. of x on y = 2
From eqn. (ii), we have

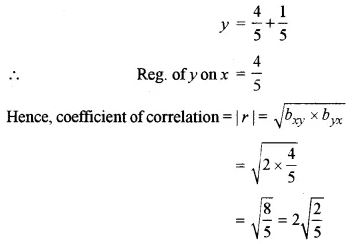
(c) The average cost function associated with producing and marketing x units of an item is given as:
AC = 2x – 11 + 50/x
Output ’ for which AC increases is:
d/dx (AC) > 0
⇒ d/dx (2x – 11 + (50/x)) > 0
⇒ 2 – (50/x²) >0
⇒ x² – 25 > 0
⇒ (x – 5)(x + 5) > 0
⇒ x > 5 [∵ x > 0]

Answer 21:

Let x and y be the number of teaching aids of type A and type B be produced by the company.
Objective Function (Z) = 80x + 120y
Subject to constraints
9x + 12y ≤ 180
or 3x + 4y ≤ 60,
x + 3y ≤ 30
and x, y ≥ 0
Table of solutions of 3x + 4y = 60

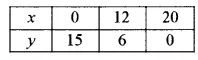
Table of solutions of x + 3y = 30

Plot the points A(0, 15), B(12, 6), C (20, 0), D(0, 10) and E(30, 0) to get the required graph as shown in the figure. Shaded region is the required feasible region and comer points of bounded feasible region are:

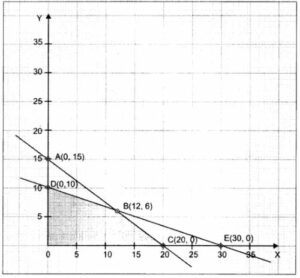
O(0, 0), B(12, 6), C(20, 0) and D(0, 10)
At O(0, 0), Z = 0 + 0 = 0
At C(20, 0), Z = 20 × 80 + 0 = 1600
At B(12, 6), Z = 12 × 80 + 120 × 6 = 1680 → Maximum
At D(0, 10), Z = 0 + 120 × 10 = 1200
Hence, maximum profit can be made by manufacturing 12 teaching aids of type A and 6 teaching aids of type B.

Answer 22:

(a) Given x + 2x + y + (y + 3) = 40
or 3x + 2y = 37 …(i)
and I = the index for the set = 122
We have I = weighted average of price-relatives

-: End of ISC Mathematic 2021 Specimen Paper for Class-12 Solved Paper :-

---

Return to – ISC Class-12 Solved Previous Year Question Paper

Thanks

Please Share with Your Friends.