ISC Maths 2020 Paper Solved Class-12 Previous Year Questions

ISC Maths 2020 Paper Solved Class-12 Previous Year Questions for practice. Step by step Solutions with section-A, B and C. Visit official website CISCE for detail information about ISC Board Class-12 Maths.

By the practice of ISC Maths 2020 Class-12 Solved Previous Year Question Paper you can get the idea of solving. Try Also other year except ISC Maths 2020 Paper Solved Class-12 Previous Year Question for more practice. Because only ISC Maths 2020 Paper is not enough for complete preparation of next council exam.

ISC Maths 2020 Paper Solved Class-12 Previous Year Questions for practice

-: Select Your Topics :-

Section-A

Section-B

Section-C

ISC Maths 2020 Paper Solved Class-12 Previous Year Questions for practice

MATHEMATICS

Time Allowed: 3 Hours
Maximum Marks: 100

(Candidates are allowed additional 15 minutes for only reading the paper. They must NOT start writing during this time.)

The Question Paper consists of three sections A, B and C.

Candidates are required to attempt all questions from Section A and all question either from Section B or Section C

Section A: Internal choice has been provided in three questions of four marks each and two questions of six marks each.

Section B: Internal choice has been provided in two question of four marks each.

Section C: Internal choice has been provided in two question of four marks each.

All working, including rough work, should be done on the same sheet as, and adjacent to, the rest of the answer.

The intended marks for questions or parts of questions are given in brackets [ ].

Mathematical tables and graphs papers are provided.

SECTION – A (80 Marks)

ISC Maths 2020 Paper (Solved )

Question 1:

i) Determine whether the binary operations $\ast$ on $R$ defined by $a \ast b = | a - b |$ is commutative. Also, find the value of $(-3) \ast 2$ .

ii) Prove that

$\tan^2( \sec^{-1} 2) + \cos^2 ( \mathrm{cosec}^{-1} 3) = 11$

iii) Without expanding at any stage, find the value of the determinant:

$\triangle = \left| \begin{array}{ccc} 20 & a & b+c \\ 20 & b & a+c \\ 20 & c & a+b \end{array} \right|$

iv) If $\begin{bmatrix} 2 & 3 \\ 5 & 7 \end{bmatrix} \begin{bmatrix} 1 & -3 \\ -2 & 4 \end{bmatrix} = \begin{bmatrix} -4 & 6 \\ -9 & x \end{bmatrix}$ , find $x$

v) Find $\frac{dy}{dx}$ if $x^3 + y^3 = 3axy$

vi) The edge of a variable cube is increasing at a rate of $10$ cm/sec. How fast is the volume of the cube increasing when the edge is $5$ cm long?

vii) Evaluate $\int \limits_{4}^{5} |x-5| dx$

viii) Form a differential equation of the family of the curves $y^2 = 4ax$

ix) A bag contains $5$ white, $7$ red and $4$ black balls. If four balls are drawn one by one with replacements, what is the probability that none is white?

x) Let A and B be two events such that $P(A) =$ $\frac{1}{2}$ $, P(B) = p$ and $P(A \cup B) =$ $\frac{3}{5}$ . Find $'p'$ and $A$ and $B$ are independent events.

Answer-1

i) For commutative

$a \ast b = b \ast a$ for all $a, b \in A$

Given $a \ast b = | a - b |$

$b \ast a = |b - a | = |a - b | = a \ast b$ . Hence proved.

$(-3) \ast 2 = |-3 - 2 | = |-5| = 5$ .

ii) Given $\tan^2( \sec^{-1} 2) + \cos^2 ( \mathrm{cosec}^{-1} 3) = 11$

Let $\sec^{-1} 2 = \theta \Rightarrow 2 = \sec \theta$

And let $\mathrm{cosec}^{-1} 3 = \alpha \Rightarrow 3 = \mathrm{cosec} \alpha$

$\therefore$ LHS $= \tan^2 \theta + \cot^2 \alpha = ( \sec^2 \theta - 1 ) + ( \mathrm{cosec}^2 \alpha -1)$

$= (2^2 -1 ) + ( 3^2 - 1 )$

$= (4-1) + ( 9-1) = 3 + 8 = 11 =$ RHS. Hence proved.

iii) Given $\triangle = \left| \begin{array}{ccc} 20 & a & b+c \\ 20 & b & a+c \\ 20 & c & a+b \end{array} \right|$

$\Rightarrow \triangle = 20 \left| \begin{array}{ccc} 1 & a & b+c \\ 1 & b & a+c \\ 1 & c & a+b \end{array} \right|$

$C_2 \rightarrow C_2+C_3$

$\Rightarrow \triangle = 20 \left| \begin{array}{ccc} 1 & a+b+c & b+c \\ 1 & b+c+a & a+c \\ 1 & c+a+b & a+b \end{array} \right|$

$\Rightarrow \triangle = 20(a+b+c) \left| \begin{array}{ccc} 1 & 1 & b+c \\ 1 & 1 & a+c \\ 1 & 1 & a+b \end{array} \right| = 0$

Note: Determinant of a Matrix with two Identical rows or columns is equal to 0. It is one of the property of determinants. If, we have any matrix with two identical rows or columns then its determinant is equal to zero.

iv) Given

$\begin{bmatrix} 2 & 3 \\ 5 & 7 \end{bmatrix} \begin{bmatrix} 1 & -3 \\ -2 & 4 \end{bmatrix} = \begin{bmatrix} -4 & 6 \\ -9 & x \end{bmatrix}$

$\Rightarrow \begin{bmatrix} 2-6 & -6+12 \\ 5-14 & -15+28 \end{bmatrix} = \begin{bmatrix} -4 & 6 \\ -9 & x \end{bmatrix}$

$\Rightarrow \begin{bmatrix} -4 & 6 \\ -9 & 13 \end{bmatrix} = \begin{bmatrix} -4 & 6 \\ -9 & x \end{bmatrix}$

$\Rightarrow x = 13$

v) $x^3 + y^3 = 3axy$

Differentiating on both sides

$3x^2 + 3y^2$ $\frac{dy}{dx}$ $= 3a \Big[ x$ $\frac{dy}{dx}$ $+ y \Big]$

$\Rightarrow x^2 + y^2$ $\frac{dy}{dx}$ $= ax$ $\frac{dy}{dx}$ $+ a y$

$\Rightarrow x^2 - ay = \Big($ $\frac{dy}{dx}$ $\Big) (ax - y^2)$

$\Rightarrow$ $\frac{dy}{dx}$ $=$ $\frac{x^2 - ay}{ax - y^2}$

vi) Let the edge be $x$

Given $\frac{dx}{dt}$ $= 10$ cm/sec

We need to find $\frac{dV}{dt}$ at $x = 5$ cm

We know $V = x^3$

$\Rightarrow$ $\frac{dV}{dt}$ $= 3x^2$ $\frac{dx}{dt}$ $= 3 \times 25 \times 10 = 750 \ cm^3/sec$

vii) $\int \limits_{4}^{5} |x-5| dx$

$= - \int \limits_{4}^{5} (x-5) dx$

$= - \Big[$ $\frac{x^2}{2}$ $- 5x \Big]_{4}^{5}$

$= - \Big[ \Big($ $\frac{5^2}{2}$ $- 5\times 5 \Big) - \Big($ $\frac{4^2}{2}$ $- 5\times 4 \Big) \Big]$

$= - \Big[$ $\frac{25}{2}$ $- 25 -$ $\frac{16}{2}$ $+ 20 \Big]$

$=$ $\frac{1}{2}$

viii) Consider the given equation.

$y^2=4ax$ … … … … … (i)

On differentiating both sides w.r.t $x$ , we get

$2y$ $\frac{dy}{dx}$ $= 4a$ … … … … … (ii)

From equations (i) and (ii), we get

$y^2 = 2y$ $\frac{dy}{dx}$ $x$

$2x$ $\frac{dy}{dx}$ $= y$

$\frac{dy}{dx}$ $=$ $\frac{y}{2x}$

ix) Balls are drawn one by one with replacements and each try is independent

Probability of not drawing a White ball $=$ $\frac{11}{16}$

Therefore the probability of not drawing white ball in four consecutive draws $= \Big($ $\frac{11}{16}$ $\Big)^4$

x) $P(A \cup B) + P(A \cap B) = P(A) + P(B)$

$\Rightarrow$ $\frac{3}{5}$ $+ P(A) .P(B) =$ $\frac{1}{2}$ $+p$

$\Rightarrow$ $\frac{3}{5}$ $+$ $\frac{1}{2}$ $p =$ $\frac{1}{2}$ $+p$

$\Rightarrow$ $\frac{1}{2}$ $p =$ $\frac{1}{10}$

$\Rightarrow p =$ $\frac{1}{5}$

Question 2:

If the function

$f : R \rightarrow R$ be defined as $f(x) =$ $\frac{3x+4}{5y-7}$ $, ( x \neq$ $\frac{7}{5}$ $)$ and

$g : R \rightarrow R$ be defined as $g(x) =$ $\frac{7x+4}{5x-3}$ $, ( x \neq$ $\frac{3}{5}$ $)$ .

Show that $(gof) = (fog) (x)$

Answer-4

If $f : A \rightarrow B$ and $g : B \rightarrow A$

$(gof) (x) = g(f(x)) = g \Big($ $\frac{3x+4}{5y-7}$ $\Big)$

$=$ $\frac{7\Big( \frac{3x+4}{5y-7} \Big)+4}{5\Big( \frac{3x+4}{5y-7} \Big)-3}$ $=$ $\frac{21x+ 28 + 20x - 28}{15x + 20 - 15x + 21}$ $=$ $\frac{41x}{41}$ $= x$

Similarly,

$(fog) (x) = f(g(x)) = f \Big($ $\frac{7x+4}{5x-3}$ $\Big)$

$=$ $\frac{3\Big( \frac{7x+4}{5x-3} \Big)+4}{5\Big( \frac{7x+4}{5x-3} \Big)-7}$ $=$ $\frac{21x + 12 + 20x - 12}{35x+20-35x+21}$ $=$ $\frac{41x}{41}$ $= x$

Hence proved.

Question 3:

a) If $\cos^{-1}$ $\frac{x}{2}$ $+ \cos^{-1}$ $\frac{y}{3}$ $= \theta$ , then prove that $9x^2 - 12 xy \cos \theta + 4 y^2 = 36 \sin^2 \theta$

b) Evaluate $\cos( 2 \cos^{-1} x + \sin^{-1} x)$ at $x =$ $\frac{1}{5}$

Answer-3

a) $\cos^{-1}$ $\frac{x}{2}$ $+ \cos^{-1}$ $\frac{y}{3}$ $= \theta$

$\cos^{-1} \Big[ \Big($ $\frac{x}{2}$ $\Big) \Big($ $\frac{y}{2}$ $\Big) -$ $\sqrt{1 - \frac{x^2}{4}} \sqrt{1 - \frac{y^2}{4}}$ $\Big] = \theta$

$\Rightarrow$ $\frac{xy}{6}$ $-$ $\frac{1}{6}$ $\sqrt{(4-x^2)(9-y^2)} = \cos \theta$

$\Rightarrow xy - \sqrt{(4-x^2)(9-y^2)} = 6 \cos \theta$

$\Rightarrow xy -6 \cos \theta = \sqrt{(4-x^2)(9-y^2)}$

Squaring both sides

$\Rightarrow x^2y^2 + 36 \cos^2 \theta - 12 xy \cos \theta = 36 - 9x^2 -4y^2 + x^2 y^2$

$\Rightarrow 9x^2 + 4y^2 - 12xy \cos \theta = 36 ( 1 - \cos \theta)$

$\Rightarrow 9x^2 + 4y^2 - 12xy \cos \theta = 36 \sin^2 \theta$

b) $\cos ( 2 \cos^{-1} x + \sin^{-1} x)$

$= \cos ( \cos^{-1} x + \cos^{-1} x + \sin^{-1} x)$

$= \cos ( \cos^{-1} x +$ $\frac{\pi}{2}$ $)$

$= - \sin ( \cos^{-1} x)$

Let $\cos^{-1} x = \theta$

$\therefore x = \cos \theta$

$= - \sin \theta$

$= -\sqrt{1 - \cos^2 \theta}$

$= - \sqrt{1 - x^2}$

$= - \sqrt{1 - \Big( \frac{1}{5} \Big)^2}$

$= -$ $\sqrt{\frac{24}{25}}$

$=-$ $\frac{\sqrt{24}}{5}$

Question 4:

Using the properties of determinants, show that

$\left| \begin{array}{ccc} x & p & q \\ p & x & q \\ q & p & x \end{array} \right| = ( x-p) (x^2 +px - 2q^2)$

Answer-4:

LHS $= \left| \begin{array}{ccc} x & p & q \\ p & x & q \\ q & q & x \end{array} \right|$

$C_1 \rightarrow C_1 - C_2$

$= \left| \begin{array}{ccc} x-p & p & q \\ p-x & x & q \\ 0 & q & x \end{array} \right|$

$= (x-p) \left| \begin{array}{rrr} 1 & p & q \\ -1 & x & q \\ 0 & q & x \end{array} \right|$

$R_2 \rightarrow R_2+R_1$

$= (x-p) \left| \begin{array}{ccc} 1 & p & q \\ 0 & x+p & 2q \\ 0 & q & x \end{array} \right|$

$= ( x-p) [ (x+p) x - 2q^2]$

$= ( x-p) [ x^2 +px - 2q^2]$ . Hence proved.

Question 5:

Verify Rolle’s theorem for the function $f(x) = - 1 + \cos x$ in the interval $[0, 2\pi ]$

Answer-5

Step I: The function is continuous in $[0, 2\pi ]$

Step II: The function is derivable in $(0, 2\pi )$

Step III: $f(0) = - 1 + \cos 0 = -1 + 1 = 0$

$f(2\pi) = - 1 + \cos 2\pi = -1 + 1 = 0$

$\therefore f(0) = f( 2\pi)$

Therefore there must be at least one point $c$ in $(0, 2\pi )$ at which $f'(c) = 0$

$f'(x) = - \sin x$

$\Rightarrow f'(c) = - \sin c = 0$

$\Rightarrow c = \pi$ $\{ c \neq 0, 2\pi \}$

Hence verified.

Question-6

If $y = e^{m \sin^{-1}x}$ , prove that $(1-x^2)$ $\frac{d^2y}{dx^2}$ $- x$ $\frac{dy}{dx}$ $= m^2y$

Answer-6

$y = e^{m \sin^{-1}x}$

Differentiating w.r.t $x$

$\Rightarrow y' = e^{m \sin^{-1}x}. m.$ $\frac{1}{\sqrt{1-x^2}}$

$\Rightarrow y' =$ $\frac{my}{\sqrt{1-x^2}}$

$\Rightarrow y' \sqrt{1-x^2} = my$

Squaring both sides

$\Rightarrow (y')^2 ( 1- x^2) = m^2 y^2$

Differentiating again

$\Rightarrow (y')^2 ( - 2x) + ( 1- x^2) 2y'y'' = 2 m^2yy'$

$\Rightarrow -x(y')^2 + ( 1 - x^2)y'y'' = m^2 y y'$

$\Rightarrow -xy' + ( 1- x^2) y'' = m^2 y$

$\Rightarrow (1-x^2) y'' - xy' = m^2y$

Question-7

(a) The equation of a tangent at $(2, 3)$ on the curve $y^2 = px^3+q$ is $y = 4x - 7$ . Find the value of $'p'$ and $'q'$ .

(b) Using L’Hospital’s rule, evaluate $\lim \limits_{x \to 0}$ $\frac{xe^x - \log (1+x)}{x^2}$

Answer-7

(a) $y^2 = px^3 + q$

Differentiating w.r.t $x$

$2 y y' = 3 px^2 + 0$

$\Rightarrow$ $\frac{dy}{dx}$ $= y' =$ $\frac{3px^2}{2y}$

Now as $y = 4x - y$ , slope of tangent $= 4$

$\therefore$ $\frac{dy}{dx}$ $= 4$

$\therefore$ $\frac{3p(2)^2}{2(3)}$ $= 4$

$\Rightarrow p = 2$

Since $(2, 3)$ is lying on the curve,

$3^2 = ( 2) 2^3 + q$

$\Rightarrow q = 9 - 16 = - 7$

(b) $\lim \limits_{x \to 0}$ $\frac{xe^x - \log (1+x)}{x^2}$

$= \lim \limits_{x \to 0}$ $\frac{xe^x + e^x - \frac{1}{1+x} }{2x}$

$=$ $\frac{0+e^0+e^0+ \frac{1^2}{1}}{2}$ $=$ $\frac{1+1+1}{2}$ $=$ $\frac{3}{2}$

Question 8:

(a) Evaluate: $\int \limits_{}^{}$ $\frac{dx}{\sqrt{5x-4x^2}}$

(b) Evaluate: $\int \limits_{}^{}$ $\sin^3 x \cos^4 x dx$

Answer-8:

(a)

$\int \limits_{}^{}$ $\frac{dx}{\sqrt{5x-4x^2}}$

Using the method of completing the square first

$5x - 4x^2 = - 4 \Big[ x^2 -$ $\frac{5}{4}$ $x \Big]$

$\Rightarrow 5x - 4x^2 = -4 \Big[ x^2 -$ $\frac{5}{4}$ $x + \Big($ $\frac{5}{8}$ $\Big)^2 - ($ $\frac{5}{8}$ $)^2 \Big]$

$\Rightarrow 5x - 4x^2 = -4 \Big[ \Big(x-$ $\frac{5}{8}$ $\Big)^2 -$ $\frac{25}{64}$ $\Big]$

$\Rightarrow 5x - 4x^2 = 4 \Big[$ $\frac{25}{64}$ $- \Big(x-$ $\frac{5}{8}$ $\Big)^2 \Big]$

Therefore

$\int \limits_{}^{}$ $\frac{dx}{\sqrt{5x-4x^2}}$

$=$ $\int \limits_{}^{}$ $\frac{dx}{\sqrt{4[ ( \frac{5}{8})^2 - ( x - \frac{5}{8})^2 ]}}$

$=$ $\frac{1}{2}$ $\int \limits_{}^{}$ $\frac{dx}{\sqrt{( \frac{5}{8})^2 - ( x - \frac{5}{8})^2 }}$

Since $\int \limits_{}^{} \frac{dx}{\sqrt{a^2 - x^2}}$ $= \sin^{-1} \Big($ $\frac{x}{a}$ $\Big) + c$

$=$ $\frac{1}{2}$ $\sin \Big[$ $\frac{x - \frac{5}{8}}{\frac{5}{8}}$ $\Big] + c$

(b)

$\int \limits_{}^{}$ $\sin^3 x \cos^4 x dx$

$=$ $\int \limits_{}^{}$ $\sin^2 x ( \cos^2 x)^2 \sin x dx$

$=$ $\int \limits_{}^{}$ $(1 - \cos^2 x) \cos^4 \sin x dx$

Let $\cos x = t$ $\therefore - \sin x dx = dt$

$= -$ $\int \limits_{}^{}$ $(1 - t^2) t^4 dt$

$= -$ $\int \limits_{}^{}$ $(t^4 - t^6) dt$

$= - \Big[$ $\frac{t^5}{5}$ $-$ $\frac{t^7}{7}$ $\Big] + c$

$= -$ $\frac{t^5}{5}$ $+$ $\frac{t^7}{7}$ $+ c$

$= -$ $\frac{\cos^5}{5}$ $+$ $\frac{\cos^7}{7}$ $+ c$

$\\$ Question 9:

Solve the differential equation $(1+x^2)$ $\frac{dy}{dx}$ $= 4x^2 - 2xy$

Answer-9

$(1+x^2)$ $\frac{dy}{dx}$ $= 4x^2 - 2xy$

$\Rightarrow$ $\frac{dy}{dx}$ $=$ $\frac{4x^2}{1+x^2}$ $- \Big($ $\frac{2x}{1+x^2}$ $\Big) y$

$\Rightarrow$ $\frac{dy}{dx}$ $+ \Big($ $\frac{2x}{1+x^2}$ $\Big) y=$ $\frac{4x^2}{1+x^2}$

$\Rightarrow$ $\frac{dy}{dx}$ $+Py = Q$

Integration Factor $= e^{ \int \limits_{}^{} p dx } = e^{ \int \limits_{}^{} \frac{2x}{1+x^2} dx } = e^{ \log |1+x^2| } = (1+x^2)$

Now $y ( 1+x^2) =$ $\int \limits_{}^{}$ $\Big($ $\frac{4x}{1+x^2}$ $\Big) (1 + x^2) dx + c$

$\Rightarrow y(1+x^2) = 4 .$ $\frac{x^3}{3}$ $+ c$

Question 10:

Three persons A, B and C shoot to hit a target. Their probability of hitting the target are $\frac{5}{6}$ , $\frac{4}{3}$ and $\frac{3}{4}$ respectively. Find the probability that

i) Exactly two persons hit the target

ii) At least one person hits the target

Answer-10

Given:

$P(A) =$ $\frac{5}{6}$ $P(\overline{A}) =$ $\frac{1}{6}$

$P(B) =$ $\frac{4}{3}$ $P(\overline{B}) =$ $\frac{1}{5}$

$P(C) =$ $\frac{3}{4}$ $P(\overline{C}) =$ $\frac{1}{4}$

i) $P($ exactly two persons hit the target $)$

$= P(A \cap B \cap \overline{C} ) + ( \overline{A} \cap B \cap C) + P( A \cap \overline{B} \cap C)$

$=$ $\frac{5}{6}$ $\times$ $\frac{4}{5}$ $\times$ $\frac{1}{4}$ $+$ $\frac{1}{6}$ $\times$ $\frac{4}{5}$ $\times$ $\frac{3}{4}$ $+$ $\frac{5}{6}$ $\times$ $\frac{1}{5}$ $\times$ $\frac{3}{4}$

$=$ $\frac{1}{6}$ $+$ $\frac{1}{10}$ $+$ $\frac{1}{8}$ $=$ $\frac{188}{480}$ $= 0.39$

ii) $P($ none of the three persons hit the target $) =$ $\frac{1}{6}$ $\times$ $\frac{1}{5}$ $\times$ $\frac{1}{4}$ $=$ $\frac{1}{120}$

Therefore Probability of at least one hitting the target $= 1 -$ $\frac{1}{120}$ $=$ $\frac{119}{120}$

Question 11:

Solve the following system of linear equations using matrices: $x - 2y = 10, 2x - y - z = 8$ and $-2y + z = 8$

Answer-11

Given equations

$x-2y=10, 2x-y-z=8$ and $-2y+z = 7$

$AX = B$

where

$A = \begin{bmatrix} 1 & -2 & 0 \\2 & -1 & -1 \\ 0 &-2 & 7 \end{bmatrix}$ $X = \begin{bmatrix} x \\ y \\ z \end{bmatrix}$ $B = \begin{bmatrix} 10 \\ 8 \\ 7 \end{bmatrix}$

$|A| = 1( -1-2) + 2(2) = -3 + 4 = 1 \neq 0$

$\because A^{-1}$ exists means there is a unique solution

$X = A^{-1}B$

$A^{-1} =$ $\frac{1}{|A|}$ $. adj A$

$=$ $\frac{1}{1}$ $\begin{bmatrix} +(-3) & -2 & +(-4) \\ -(-2) & +1 & -(-2) \\ +2 & -(-1) & +(3) \end{bmatrix}'$ $= \begin{bmatrix} -3 & -2 & -4 \\ 2 & 1 & 2 \\ 2 & 1 & 3 \end{bmatrix}'$ $= \begin{bmatrix} -3 & 2 & 2 \\ -2 & 1 & 1 \\ -4 & 2 & 3 \end{bmatrix}$

$\therefore X = \begin{bmatrix} -3 & 2 & 2 \\ -2 & 1 & 1 \\ -4 & 2 & 3 \end{bmatrix} \begin{bmatrix} 10 \\ 8 \\ 7 \end{bmatrix}$ $= \begin{bmatrix} -30+16+14 \\ -20+8+7 \\ -40+16+21 \end{bmatrix}$ $= \begin{bmatrix} 0 \\ -5 \\ -3 \end{bmatrix}$

$\therefore x = 0, y = -5 , z = -3$

Question 12:

(a) Show that the radius of a closed right circular cylinder of a given surface area and maximum volume to is equal to half of its height.

(b) Prove that the area of a right angled triangle of given hypotenuse is maximum when the triangle is isosceles.

Answer-12

(a) $A = 2\pi r h + 2 \pi r^2 \Rightarrow h =$ $\frac{A - 2\pi r^2}{2 \pi r}$

$V = \pi r^2 h = \pi r^2 \Big($ $\frac{A - 2\pi r^2}{2 \pi r}$ $\Big) =$ $\frac{r}{2}$ $[A - 2\pi r^2]$

$\therefore V =$ $\frac{Ar}{2}$ $- \pi r^3$

Differentiating w.r.t. $r$

$\frac{dV}{dr}$ $=$ $\frac{A}{2}$ $- 3\pi r^2$

Now $\frac{dV}{dr}$ $= 0$

$\therefore$ $\frac{A}{2}$ $- 3\pi r^2 = 0$

$\Rightarrow$ $\frac{A}{2}$ $= 3 \pi r^2$

$\Rightarrow$ $\frac{A}{6\pi}$ $= r^2$

$\Rightarrow$ $r =$ $\sqrt{\frac{A}{6\pi}}$

Differentiating again w.r.t. $r$

$\frac{d^2V}{dr^2}$ $= 0 - 6 \pi r$ which is negative. Hence volume maximum at $r =$ $\sqrt{\frac{A}{6\pi}}$

$A = 2\pi \Big($ $\sqrt{\frac{A}{6\pi}}$ $\Big) h + 2 \pi \Big($ $\sqrt{\frac{A}{6\pi}}$ $\Big)^2$

$\Rightarrow A = 2\pi \Big($ $\sqrt{\frac{A}{6\pi}}$ $\Big) h + 2 \pi \Big($ $\frac{A}{6\pi}$ $\Big)$

$\Rightarrow$ $\frac{2}{3}$ $A = 2 \pi \Big($ $\sqrt{\frac{A}{6\pi}}$ $\Big) h$

$\Rightarrow h =$ $\frac{\frac{2}{3}A}{2\pi \sqrt{\frac{A}{6\pi}}}$ $=$ $\sqrt{\frac{2A}{3\pi}}$

Now $r =$ $\sqrt{\frac{A}{6\pi}}$ and $h =$ $\sqrt{\frac{2A}{3\pi}}$

$\therefore$ $\frac{r}{h}$ $=$ $\sqrt{\frac{A}{6\pi}}$ $\times$ $\sqrt{\frac{3\pi}{2A}}$ $=$ $\frac{1}{2}$

$\therefore r =$ $\frac{h}{2}$ . Hence proved.

(b)

$A =$ $\frac{1}{2}$ $xy$

We know $x^2 + y^2 = H^2 \Rightarrow y = \sqrt{H^2 - x^2}$

$A =$ $\frac{1}{2}$ $x \sqrt{H^2 - x^2}$

Differentiating w.r.t. $x$

$\frac{dA}{dx}$ $=$ $\frac{1}{2}$ $\Big[ 2 \Big($ $\frac{-2x}{2(\sqrt{H^2-x^2})}$ $\Big) + \sqrt{H^2 - x^2} (1) \Big]$

$=$ $\frac{1}{2}$ $\Big[$ $\frac{-x^2+H^2-x^2}{\sqrt{H^2 - x^2}}$ $\Big] = 0$

$\Rightarrow H^2 = 2x^2$

$\frac{H}{\sqrt{2}}$ $= x$

Differentiating again w.r.t. $x$ we get less than 0 at $x =$ $\frac{H}{\sqrt{2}}$ . Hence it’s maximum.

$\therefore x^2 + y^2 = H^2$

$\frac{H^2}{2}$ $+ y^2 = H^2$

$y =$ $\frac{H}{\sqrt{2}}$ $= x$

Therefore the triangle is an isosceles triangle.

Question 13

(a) Evaluate: $\int \limits_{}^{}$ $\tan^{-1}$ $\sqrt{\frac{1-x}{1+x}}$ $dx$

(b) Evaluate: $\int \limits_{}^{}$ $\frac{2x+7}{x^2 - x - 2}$ $dx$

Answer-13

(a)

$I =$ $\int \limits_{}^{}$ $\tan^{-1}$ $\sqrt{\frac{1-x}{1+x}}$ $dx$

Let $x = \cos 2\theta \Rightarrow dx = - 2 \sin 2 \theta d\theta$

$\therefore$ $= -2$ $\int \limits_{}^{}$ $\tan^{-1}$ $\sqrt{\frac{1-\cos 2\theta}{1+\cos 2\theta}}$ $\sin 2 \theta d\theta$

$= -2$ $\int \limits_{}^{}$ $\tan^{-1}$ $\sqrt{\frac{2 \sin^2 \theta}{2\cos^2 \theta}}$ $\sin 2 \theta d\theta$

$= -2$ $\int \limits_{}^{}$ $\tan^{-1} (\tan \theta) \sin 2\theta d\theta$

$= -2$ $\int \limits_{}^{}$ $\theta \sin 2\theta d\theta$

Let $2\theta = y \Rightarrow 2 d\theta = dy$

$= -$ $\frac{1}{2}$ $\int \limits_{}^{}$ $y \sin y dy$

$= -$ $\frac{1}{2}$ $\Big[ y$ $\int \limits_{}^{}$ $\sin y dy -$ $\int \limits_{}^{}$ $\frac{d(y)}{dy}$ $\int \limits_{}^{}$ $\sin y dy + c \Big]$

$= -$ $\frac{1}{2}$ $\Big[ -y \cos y +$ $\int \limits_{}^{}$ $\cos y dy + c \Big]$

$= -$ $\frac{1}{2}$ $\Big[ -y \cos y + \sin y + c \Big]$

$=$ $\frac{1}{2}$ $y \cos y - \frac{1}{2} \sin y + c'$

$=$ $\frac{1}{2}$ $(2\theta) \cos 2\theta - \frac{1}{2} \sin 2\theta + c'$

Where $\theta =$ $\frac{1}{2}$ $\cos^{-1}x$

(b) $\int \limits_{}^{}$ $\frac{2x+7}{x^2 - x - 2}$ $dx$

$=$ $\int \limits_{}^{}$ $\frac{2x-1}{x^2 - x - 2}$ $dx$ $+$ $\int \limits_{}^{}$ $\frac{8}{x^2 - x - 2}$ $dx$

$=$ $\int \limits_{}^{}$ $\frac{2x-1}{x^2 - x - 2}$ $dx$ $+ 8$ $\int \limits_{}^{}$ $\frac{1}{x^2 - x - 2}$ $dx$

$=$ $\int \limits_{}^{}$ $\frac{2x-1}{x^2 - x - 2}$ $dx$ $+ 8$ $\int \limits_{}^{}$ $\frac{1}{(x-2)(x+1)}$ $dx$

$=$ $\int \limits_{}^{}$ $\frac{2x-1}{x^2 - x - 2}$ $dx$ $+ \frac{8}{3}$ $\int \limits_{}^{}$ $\Big[$ $\frac{1}{(x-2)} - \frac{1}{(x+1)}$ $\Big] dx$

Now, if $u = x^2 - x + 1 \Rightarrow$ $\frac{du}{dx}$ $= 2x-1 \Rightarrow dx =$ $\frac{1}{2x-1}$ $du$

$\therefore$ $\int \limits_{}^{}$ $\frac{2x-1}{x^2 - x - 2}$ $=$ $\int \limits_{}^{}$ $\frac{1}{u}$ $du = \log |u| = \log |x^2 - x - 2 |$

Now, if $u = x-2 \Rightarrow$ $\frac{du}{dx}$ $= 1 \Rightarrow dx = du$

$\therefore$ $\int \limits_{}^{}$ $\frac{1}{x- 2}$ $=$ $\int \limits_{}^{}$ $\frac{1}{u}$ $du = \log |u| = \log |x - 2 |$

Now, if $u = x+1 \Rightarrow$ $\frac{du}{dx}$ $= 1 \Rightarrow dx = du$

$\therefore$ $\int \limits_{}^{}$ $\frac{1}{x+1}$ $=$ $\int \limits_{}^{}$ $\frac{1}{u}$ $du = \log |u| = \log |x +1|$

$\therefore$ $\int \limits_{}^{}$ $\frac{2x+7}{x^2 - x - 2}$ $dx = \log |x^2 - x - 2 | +$ $\frac{8}{3}$ $[ \log |x - 2 | - \log |x +1| ]$

Question 14

The probability that a bulb produced in a factory will fuse after $150$ days is $0.05$ . Find the probability that out of five such bulbs:

i) None will fuse after $150$ days of use

ii) Not more than one will fuse after $150$ days of use

iii) More than one will fuse after $150$ days of use

iv) At least one will fuse after $150$ days of use

Answer-14

Let $X$ be the number of bulbs that will fuse after $150$ days of use in an experiment of $5$ trials.

$p = 0.05$ $q = 1 - 0.05 = 0.95$ $n = 5$

$\therefore p(X=x) = {^nC_x} q^{n-x} p^x = {^5C_x} (0.95)^{5-x}(0.05)^x$

i) $P(none) = P(X=0) = {^5C_0} (0.95)^{5-0}(0.05)^0 = (0.95)^5$

ii) $P(X \leq 1) = P(X=0) + P(X=1)$

$= {^5C_0} (0.95)^{5-0}(0.05)^0 + {^5C_1} (0.95)^{5-1}(0.05)^1 = (0.95)^4 \times 1.2$

iii) $P(X > 1) = 1 - P(X \leq 1) = 1 - (0.95)^4 \times 1.2$

iv) $P(X = \ at \ least \ one \ will \ fuse ) = 1 - P(X =0) = 1 -(0.95)^5$

Section-B (20 Marks)

ISC Maths 2020 Paper Solved Class-12 Previous Year Questions

Question 15:

(a) Write a vector of magnitude 18 units in the direction of the vector $\hat{i}-2\hat{j} - 2\hat{k}$ .

(b) Find the angle between the two lines

$\frac{x+1}{2}$ $=$ $\frac{y-2}{5}$ $=$ $\frac{z+3}{4}$ and $\frac{x-1}{5}$ $=$ $\frac{y+2}{2}$ $=$ $\frac{z-1}{-5}$

(c) Find the equation of the plane passing through the point $(2, -3, 1)$ and perpendicular to the line joining the points $(4, 5, 0)$ and $(1, -2, 4)$ .

Answer-15

(a)

$\overrightarrow{a} = \hat{i}-2\hat{j} - 2\hat{k}$

$\hat{a} =$ $\frac{\overrightarrow{a}}{|\overrightarrow{a}|}$ $=$ $\frac{\hat{i}-2\hat{j} - 2\hat{k}}{\sqrt{1+4+4}}$ $=$ $\frac{\hat{i}-2\hat{j} - 2\hat{k}}{3}$

$\overrightarrow{b} = |\overrightarrow{b}| \hat{a}$

$\Rightarrow \overrightarrow{b} = 18 [$ $\frac{1}{3}$ $( \hat{i}-2\hat{j} - 2\hat{k}) ]$

$\Rightarrow \overrightarrow{b} = 6\hat{i}-12\hat{j} - 12\hat{k}$

(b)

$L_1 :$ $\frac{x+1}{2}$ $=$ $\frac{y-2}{5}$ $=$ $\frac{z+3}{4}$

$\Rightarrow a_1 = 2, b_1 = 5 , c_1 = 4$ and $a_2 = 5, b_2 = 2 , c_2 = -5$

Angle between $L_1$ and $L_2$ is given by

$\cos \theta = \Big|$ $\frac{a_1a_2+b_1b_2+c_1c_2}{\sqrt{ {a_1}^2+ {b_1}^2 + {c_1}^2 } \sqrt{ {a_2}^2+ {b_2}^2 + {c_2}^2 } }$ $\Big|$

$= \Big|$ $\frac{2 \times 5+ 5 \times 2 + 4 \times (-5) }{\sqrt{ 4+25+16 } \sqrt{ 25+4+16 }}$ $\Big|$

$= \Big|$ $\frac{10+10-20}{45}$ $\Big| = 0$

$\Rightarrow \cos \theta = 0 \Rightarrow \theta = 90^{\circ}$ or $\frac{\pi}{2}$

(c) Given point $( 2, -3, 1$ ). d.rs of line joining the points $A( 4, 5, 0)$ and $B ( 1, -2, 4)$ is $< 1-4, -2-5, 0-4 >$ i.e. $< -3, -7, -4>$ or $<3, 7, 4 >$

Equation of plant passing through $(2, -3, 1)$ is

$A(x-x_1) + B ( y - y_1) + c( z-z_1) = 0$

$\Rightarrow 3(x-2) + 7 ( y+3) + 4 ( z-1) = 0$

$\Rightarrow 3x + 7y + 4z + 11=0$

Question 16:

(a) Prove that $\overrightarrow{a} . [ (\overrightarrow{b}+\overrightarrow{c}) \times (\overrightarrow{a} + 3\overrightarrow{b} + 4 \overrightarrow{c})] = [\overrightarrow{a}\ \overrightarrow{b}\ \overrightarrow{c} ]$

(b) Using vectors, find the area of the triangle whose vertices are: $A ( 3, -1, 2) , B ( 1, -1, -3)$ and $C( 4, -3, 1)$ .

Answer-16

(a) We have $\overrightarrow{a} . [ (\overrightarrow{b}+\overrightarrow{c}) \times (\overrightarrow{a} + 3\overrightarrow{b} + 4 \overrightarrow{c})]$

$= \overrightarrow{a} . [ \overrightarrow{b} \times \overrightarrow{a} + 3( \overrightarrow{b} \times \overrightarrow{b}) + 4 (\overrightarrow{b} \times \overrightarrow{c}) + \overrightarrow{c} \times \overrightarrow{a} + 3( \overrightarrow{c} \times \overrightarrow{b}) + 4 (\overrightarrow{c} \times \overrightarrow{c}) ]$

$= \overrightarrow{a} . [ \overrightarrow{b} \times \overrightarrow{a} + 4( \overrightarrow{b} \times \overrightarrow{c}) + \overrightarrow{c} \times \overrightarrow{a} + 3( \overrightarrow{c} \times \overrightarrow{b}) ]$

$= \overrightarrow{a} . [ \overrightarrow{b} \times \overrightarrow{a} + 4( \overrightarrow{b} \times \overrightarrow{c}) + \overrightarrow{c} \times \overrightarrow{a} - 3( \overrightarrow{b} \times \overrightarrow{c}) ]$

$= \overrightarrow{a} . [ \overrightarrow{b} \times \overrightarrow{a} + \overrightarrow{b} \times \overrightarrow{c} + \overrightarrow{c} \times \overrightarrow{a} ]$

$= \overrightarrow{a}( \overrightarrow{b} \times \overrightarrow{a}) + \overrightarrow{a}( \overrightarrow{b} \times \overrightarrow{c}) + \overrightarrow{a} (\overrightarrow{c} \times \overrightarrow{a}) ]$

$= 0 + [ \overrightarrow{a}\ \overrightarrow{b}\ \overrightarrow{c}] + 0$

$= [ \overrightarrow{a}\ \overrightarrow{b}\ \overrightarrow{c}] =$ RHS. Hence proved.

(b) Given $A ( 3, -1, 2) , B ( 1, -1, -3)$ and $C( 4, -3, 1)$ .

$\overrightarrow{AB} = (1-3) \hat{i}+ ( -1 + 1 ) \hat{j}+ (-3-2) \hat{k} = 2\hat{i}+ 0\hat{j} -5\hat{k}$

$\overrightarrow{AC} = (4-3) \hat{i}+ ( -3 + 1 ) \hat{j}+ (1-2) \hat{k} = \hat{i}-2\hat{j} -\hat{k}$

Area of $\triangle ABC = \frac{1}{2} | \overrightarrow{AB} \times \overrightarrow{AC} |$

$\overrightarrow{AB} \times \overrightarrow{AC} = \left| \begin{array}{rrr} \hat{i} & \hat{j} & \hat{j} \\ -2 & 0 & -5 \\ 1 & -2 & -1 \end{array} \right|$

$= \hat{i} ( 0 - 10) - \hat{j} (2+5) + \hat{k} (4-0)$

$= -10\hat{i} -7\hat{j} + 4\hat{k}$

$\therefore$ Area of $\triangle ABC = \frac{1}{2} \sqrt{100+49+16} = \frac{1}{2} \sqrt{165}$ sq. units.

Question 17:

(a) Find the image of the point $(3, -2, 1)$ on the plant $3x-y+4z=2$

(b) Determine the equation of the line passing through the point $( -1, 3, -2)$ and perpendicular to the lines $\frac{x}{1}$ $=$ $\frac{y}{2}$ $=$ $\frac{z}{3}$ and $\frac{x+2}{-3}$ $=$ $\frac{y-1}{2}$ $=$ $\frac{z+1}{5}$

Answer-17

(a) The directional ratios of normal to plane are $<3, -1, 4>$

$\therefore$ Equation of $AB =$ $\frac{x-3}{3}$ $=$ $\frac{y+2}{-1}$ $=$ $\frac{z-1}{4}$ $= k$

Coordinate of a general point on line $AB$ is $( 3k+3, -k-2, 4k+1)$

This point lies on the plane $3x -y + 4z=2$

$\Rightarrow 9k + 9 + k + 2 + 16k + 4 = 2$

$\Rightarrow 26k+15=2$

$\Rightarrow k = -$ $\frac{13}{26}$ $= -$ $\frac{1}{2}$

$\therefore$ coordinate of $M$ are

$\Big( 3 \times (-$ $\frac{1}{2}$ $) + 3,$ $\frac{1}{2}$ $- 2, 4 \times (-$ $\frac{1}{2}$ $) + 1 \Big) = \Big($ $\frac{3}{2}$ $, -$ $\frac{3}{2}$ $, -1 \Big)$

(b) Equation of line passing through the point $( -1, 3, -2)$ is

$L:$ $\frac{x+1}{a}$ $=$ $\frac{y-3}{b}$ $=$ $\frac{z+2}{c}$ where $a, b, c$ are direction ratios of the line.

Line $L$ is $\perp$ to lines $\frac{x}{1}$ $=$ $\frac{y}{2}$ $=$ $\frac{z}{3}$ and $\frac{x+2}{-3}$ $=$ $\frac{y-1}{2}$ $=$ $\frac{z+1}{5}$

The directional ratios of like $\perp$ can be found by solving equation

$\frac{a}{10-6}$ $=$ $\frac{b}{-9-5}$ $=$ $\frac{c}{2+6}$

$\Rightarrow$ $\frac{a}{4}$ $=$ $\frac{b}{-14}$ $=$ $\frac{c}{8}$

$\Rightarrow$ $\frac{a}{2}$ $=$ $\frac{b}{-7}$ $=$ $\frac{c}{4}$

Therefore the equation of line L is $\frac{x+1}{2}$ $=$ $\frac{y-3}{-7}$ $=$ $\frac{z+2}{4}$

Question 18:

Draw a rough sketch of the curves $y^2 = x$ and $y^2 = 4 - 3x$ and find the area enclosed between them.

Answer-18

$y^2 = x$ … … … … … i) (equation of a parabola)

$y^2 = 4 - 3x$ … … … … … ii) (equation of a parabola)

Points of intersection:

$4-3x = x \Rightarrow x = 1$

Therefore $y^2 = 1 \Rightarrow y = \pm 1$

$y^2 = -3x + 4 = -3 ( x -$ $\frac{4}{3}$ $)$

The vertex $L$ of this parabola is $($ $\frac{4}{3}$ $, 0)$ . It cuts the y axis at $A (0, 2)$ and $B (0, -2)$

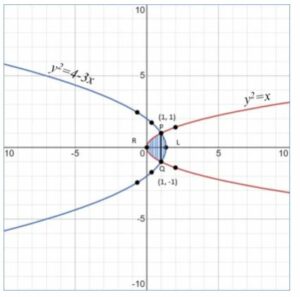
Let $PQ$ cut the x-axis at $R$

Total area $= POQLP = 2$ area of $PORLP$

$= \Big[ \int \limits_{0}^{1} \sqrt{x} dx + \int \limits_{1}^{4/3} \sqrt{4-3x} dx \Big]$

$= 2 \Big[ \Big($ $\frac{x^{\frac{3}{2}}}{\frac{3}{2}}$ $\Big)_{0}^{1} + \Big($ $\frac{2(4-3x)^\frac{3}{2}}{(-3)\times 3}$ $\Big)_{1}^{4/3}\Big]$

$= 2 \Big[ \Big($ $\frac{2}{3}$ $-0 \Big) -$ $\frac{2}{9}$ $(0-1) \Big]$

$= 2 \Big[$ $\frac{2}{3}$ $+$ $\frac{2}{9}$ $\Big]$

$=$ $\frac{16}{9}$ sq. units

Section – C (20 Marks)

ISC Maths 2020 Paper (Solved ) Previous Year Questions for Class-12

Question 19:

(a)

The selling price of a commodity is fixed at Rs. $60$ and its cost function is $C(x) = 35x + 250$

i) Determine it’s profit margin

ii) Find the break even point

(b)

The Revenue function is given by $R(x) = 100x - x^2 -x^3$ . Find

i) The demand function

ii) Marginal revenue function

(c)

For the lines of regression $4x - 2y = 4$ and $2x-3y+6 = 0$ , find the value of $'x'$ and the mean of $'y'$

Answer-19

(a)

$C(x) = 35x + 250$ and $S(x) = 60x$

i) $P(x) = S(x) - C(x) = 60x-35x-250 = 25x-250 = 25( x - 10)$

ii) At break even point $P(x) = 0$

$\therefore 60x = 35x + 250$

$\Rightarrow 25x = 250 \Rightarrow x = 10$

(b)

i) $R(x) = P(x).x$

$P(x) =$ $\frac{R(x)}{x}$ $=$ $\frac{100x - x^2 -x^3}{x}$ $= 100 - x - x^2$

$\therefore P(x) = 100 - x - x^2$

ii) $MR =$ $\frac{dR}{dx}$ $= 100-2x-3x^2$

$\therefore MR = 100-2x-3x^2$

(c)

$4x - 2y = 4$ … … … … … i)

$2x-3y=-6$ … … … … … ii)

Solving i) and ii) we get $y = 4$ and $x = 3$

$\therefore \overline{x} = 3$ and $\overline{y} = 4$

Question 20:

(a) The correlation coefficient between $x$ and $y$ is $0.6$ . If the variance of $x = 225$ and the variance of $y$ is $400$ , mean of $x$ is $10$ and the mean of $y = 20$ , find:

i) the equations of two regression lines

ii) the expected value of $y$ when $x = 2$

(b) Find the regression coefficient $b_{yx}, b_{xy}$ and the correlation coefficient $'r'$ for the following data: $( 2, 8), ( 6, 8), ( 4, 5), ( 7, 6), (5, 2)$

Answer-20

(a)

Given $r = 0.6$ $\overline{x} =10$ $\overline{y} =10$

$Var(x) = 225$ $Var(y) = 400$

$\sigma_x = 15$ $\sigma_y = 20$

$b_{yx} = r$ $\frac{\sigma_y}{\sigma_x}$ $= 0.6 \times$ $\frac{20}{15}$ $=$ $\frac{4}{5}$

$b_{xy} = r$ $\frac{\sigma_x}{\sigma_y}$ $= 0.6 \times$ $\frac{15}{20}$ $=$ $\frac{9}{20}$

i) Line of regression of $y$ on $x$

$y - \overline{y} = b_{yx} (x - \overline{x})$

$\Rightarrow y - 20 =$ $\frac{4}{5}$ $(x - 10)$

$\Rightarrow 5y - 100 = 4x - 40$

$\Rightarrow 4x - 5y + 60 = 0$

Line of regression of $x$ on $y$

$x - \overline{x} = b_{xy} (y - \overline{y})$

$\Rightarrow y - 10 =$ $\frac{9}{20}$ $(y - 20)$

$\Rightarrow 20x-200 = 9y - 180$

$\Rightarrow 20x - 9 y - 20 = 0$

ii) At $x = 2, 4(2) - 5y +60 = 0 \Rightarrow 5y = 68 \Rightarrow y =$ $\frac{68}{5}$

(b)

$x$	$x^2$	$y$	$y^2$	$xy$
2	4	8	64	16
6	36	8	64	48
4	14	5	25	20
7	49	6	36	42
5	25	2	4	10
$\Sigma x = 24$	$\Sigma x^2 = 130$	$\Sigma y = 29$	$\Sigma y^2 = 193$	$\Sigma xy = 136$

$b_{yx} =$ $\frac{\Sigma xy - \frac{1}{n} \Sigma x \Sigma y}{\Sigma x^2 - \frac{1}{n} ( \Sigma x)^2}$ $=$ $\frac{136 - \frac{1}{5} (24)(29)}{130 - \frac{1}{5} (24)^2}$ $= -$ $\frac{3.2}{14.8}$ $= -0.22$

$b_{xy} =$ $\frac{\Sigma xy - \frac{1}{n} \Sigma x \Sigma y}{\Sigma y^2 - \frac{1}{n} ( \Sigma y)^2}$ $=$ $\frac{136 - \frac{1}{5} (24)(29)}{193 - \frac{1}{5} (29)^2}$ $= -$ $\frac{3.2}{24.8}$ $= -0.13$

$|x| =\sqrt{b_{yx}b_{xy}} = \sqrt{(-0.22)(-0.13)} = \pm \sqrt{0.0286} = \pm 0.17$

Since $r$ has the same sign as regressions coefficient $\therefore r(x, y) = -0.17$

Question 21:

(a) The marginal cost of the production of the commodity is $30+2x$ , it is know that fixed cost are Rs. $200$ , find;

i) The total cost

ii) The cost of increasing output from $100$ to $200$ units

(b) The total cost function of the firm is given by $C(x) =$ $\frac{1}{3}$ $x^3 - 5x^2 + 30 x - 15$ where the selling price per unit is given as Rs. $6$ . Find for what value of $x$ will the profit be maximum.

Answer-21

(a)

i) $MC =$ $\frac{dc}{dx}$ $=30 + 2x$

Integrating both sides

$C = \int \limits_{}^{} ( 30+2x) dx$

$\Rightarrow C = 30x + x^2 + k$

When $x = 0, C = 200$

$\therefore 200 = 0 + 0 + k$

$\Rightarrow k = 200$

$\therefore$ cost function $C(x) = 30x + x^2 + 200$

ii) Cost of increasing the output from $100$ to $200$ units

$= \int \limits_{100}^{200} (30+2x) dx$

$= {\Big[ 30x + x^2 \Big]}_{100}^{200}$

$= [ 30(200) + 200^2] - [ 30(100)+100^2]$

$= 33000$

$\therefore$ cost of increasing output $= 33000$ Rs.

(b)

$C(x) =$ $\frac{1}{3}$ $x^3 - 5x^2 + 30 x - 15$

$S(x) = 6x$

$\therefore P(x) = S(x) - C(x) = 5x^2 -$ $\frac{1}{3}$ $x^3 - 24 x + 15$

$\frac{dP}{dx}$ $= 10 x - x^2 - 24$

Put $\frac{dP}{dx}$ $= 0$

$\Rightarrow x^2 - 10x + 24 = 0$

$\Rightarrow (x-4)(x-6) = 0$

$\Rightarrow x = 4 \ or \ 6$

$\frac{d^2P}{dx^2}$ $= 10- 2x$

$\frac{d^2P}{dx^2}$ $\Big|_{x=4} = 10 - 2(4) = 2 > 0$ [ Therefore $P$ is minimum at $x = 4$ ]

$\frac{d^2P}{dx^2}$ $\Big|_{x=6} = 10 - 2(6) = -2 < 0$ [ Therefore $P$ is maximum at $x = 6$ ]

Question 22:

A company uses three machines to manufacture two types of shirts, half sleeves shirts and full sleeves shirt. The number of hours required per week on machines $M_1, M_2$ and $M_3$ for one shirt of each type is given in the following table:

	$M_1$	$M_2$	$M_3$
Half Sleeves Shirt	1	2	8/5
Full Sleeves Shirt	2	1	8/5

None of the machines can be in operations for more than $40$ hours per week. The profit on each half sleeves shirt is Rs. $1$ and the profit on each full sleeves shirt is Rs. $1.50$ .

How many of each type of shirts should be made per week to maximize the company’s profit.

Answer-22

Let the number of half sleeves shirts produced $= x$

Let the number of full sleeves shirts produced $= x$

Maximize $Z = x + 1.5 y$

Constraints:

$x+2y \leq 40$

$2x+y \leq 40$

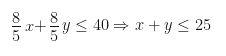
Now draw the three lines:

$x+2y=40$			$2x+y=40$			$x+y=25$
$x$	0	40	$x$	0	20	$x$	0	25
$y$	20	0	$y$	40	0	$y$	25	0

$Z = x + 1.5 y$
A( 0, 20)	30
B(10, 15)	32.5
C( 15, 10)	30
D( 20, 0)	20

Therefore the maximum value is at $B(10, 15)$ . Hence the company should make $10$ Half Sleeves Shirts and $15$ Full Sleeves Shirts to maximize profit.

-: End of ISC Maths 2020 Class-12 Solved Previous Year Question Paper :-

Return to – ISC Class-12 Solved Previous Year Question Paper

Thanks

Please Share with Your Friends

Frequency Distribution MCQs Class 9 RS Aggarwal Goyal Brothers ICSE Maths Solutions

Frequency Distribution Class 9 RS Aggarwal Exe-15 Goyal Brothers ICSE Maths Solutions

Pythagoras Theorem MCQs Class 9 RS Aggarwal Goyal Brothers ICSE Maths Solutions

ISC Maths 2020 Paper Solved Class-12 Previous Year Questions for practice

ISC Maths 2020 Paper Solved Class-12 Previous Year Questions for practice

SECTION – A (80 Marks)

Question 1:

Answer-1

Question 2:

Answer-4

Question 3:

Answer-3

Question 4:

Answer-4:

Question 5:

Answer-5

Question-6

Answer-6

Question-7

Question 8:

Answer-8:

Question 9:

Answer-9

Question 10:

Answer-10

Question 11:

Answer-11

Question 12:

Answer-12

Question 13

Answer-13

Question 14

Answer-14

Section-B (20 Marks)

Question 15:

Answer-15

Question 16:

Answer-16

Question 17:

Answer-17

Question 18:

Answer-18

Section – C (20 Marks)

Question 19:

Answer-19

Question 20:

Answer-20

Question 21:

Answer-21

Question 22:

Answer-22

Leave a Comment Cancel reply

$\\$ Question 9: