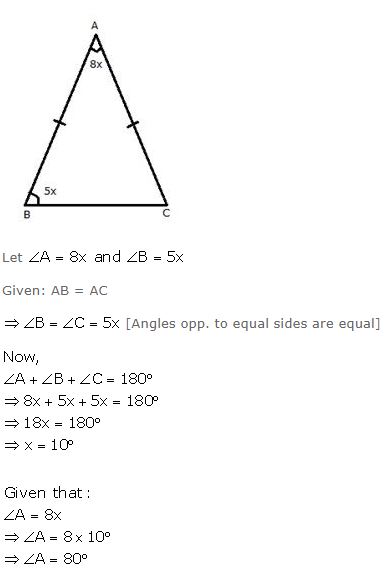Isosceles Triangles Concise Class-9th Selina ICSE Mathematics Solutions Chapter-10 by RK Bansal . We provide step by step Solutions of Exercise / lesson-10 Isosceles Triangles for ICSE Class-9 Concise Selina Mathematics by R K Bansal.
Our Solutions contain all type Questions with Exe-10 A and Exe-10 B, to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-9 Mathematics .
Isosceles Triangles Concise Class-9th Selina ICSE Mathematics Solutions Chapter-10 by R K Bansal.
–: Select Topics :–
Exercise – 10 A, Isosceles Triangles Concise Class-9th Selina ICSE Mathematics Solutions by RK Bansal
Question 1
In the figure alongside,
……………
AB = AC
A = 48o and
Angel ACD = 18o.
Show that BC = CD.
Answer

Question 2
Calculate:
(i) ∠ADC
(ii) ∠ABC
(iii) ∠BAC
Answer

Question 3
In the following figure, AB = AC; BC = CD and DE is parallel to BC. Calculate:
(i) ∠CDE
(ii) ∠ DCE
Answer

Question 4
Calculate x:
(i)………………….
(ii)…………………….
Answer


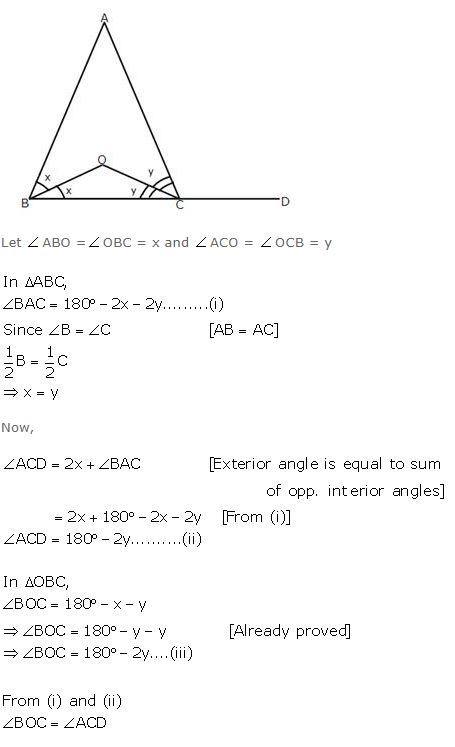
Question 5
In the figure, given below, AB = AC. Prove that: BOC = ACD.
Answer
Question 6
In the figure given below, LM = LN; angle PLN = 110o. Calculate:
(i) ∠LMN
(ii) ∠MLN
Answer

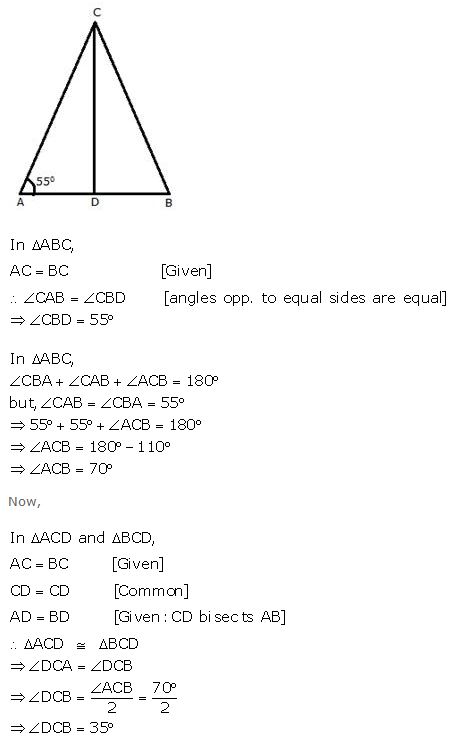
Question 7
An isosceles triangle ABC has AC = BC. CD bisects AB at D and CAB = 55o.
Find: (i) ∠DCB (ii) ∠CBD.
Answer
Question 8
Find x:
…………………..
Answer

Question 9
In the triangle ABC, BD bisects angle B and is perpendicular to AC. If the lengths of the sides of the triangle are expressed in terms of x and y as shown, find the values of x and y.
Answer

Question 10
In the given figure; AE // BD, AC // ED and AB = AC. Find ∠a, ∠b and ∠c.
Answer
Question 11
In the following figure; AC = CD, AD = BD and ∠C = 58o.
Find angle CAB.
Answer
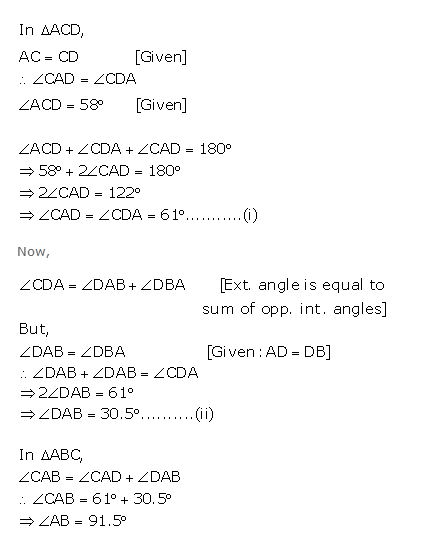
Question 12
In the figure of q. no. 11 given above, if AC = AD = CD = BD; find angle ABC.
Answer

Question 13
In triangle ABC; AB = AC and ∠A : ∠B = 8 : 5; find angle A.
Answer
Question 14
In triangle ABC; ∠A = 60o, ∠C = 40o, and bisector of angle ABC meets side AC at point P. Show that BP = CP.
Answer
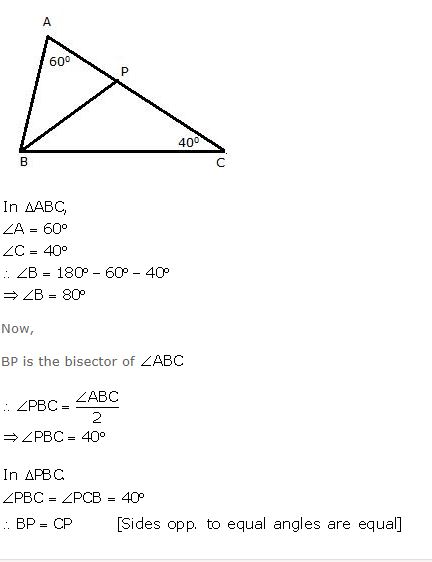
Question 15
In triangle ABC; angle ABC = 90o and P is a point on AC such that ∠PBC = ∠PCB. Show that: PA = PB.
Answer
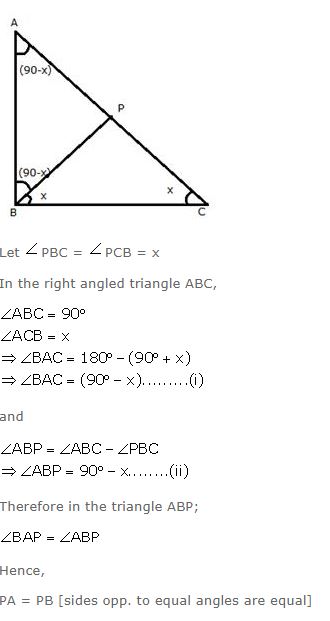
Question 16
ABC is an equilateral triangle. Its side BC is produced upto point E such that C is mid-point of BE. Calculate the measure of angles ACE and AEC.
Answer
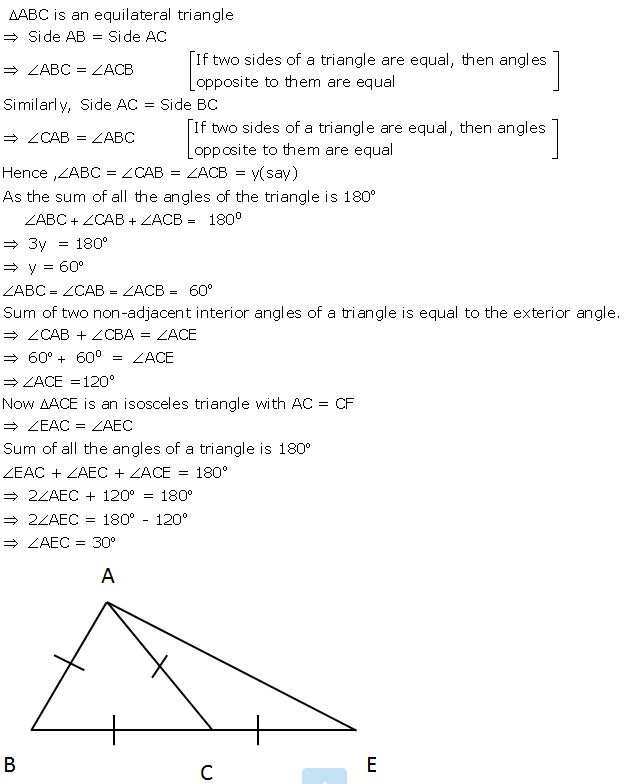
Question 17
In triangle ABC, D is a point in AB such that AC = CD = DB. If ∠B = 28°, find the angle ACD.
Answer

Question 18
In the given figure, AD = AB = AC, BD is parallel to CA and angle ACB = 65°. Find angle DAC.
Answer

Question 19
Prove that a triangle ABC is isosceles, if:
(i) altitude AD bisects angles BAC, or
(ii) bisector of angle BAC is perpendicular to base BC.
Answer
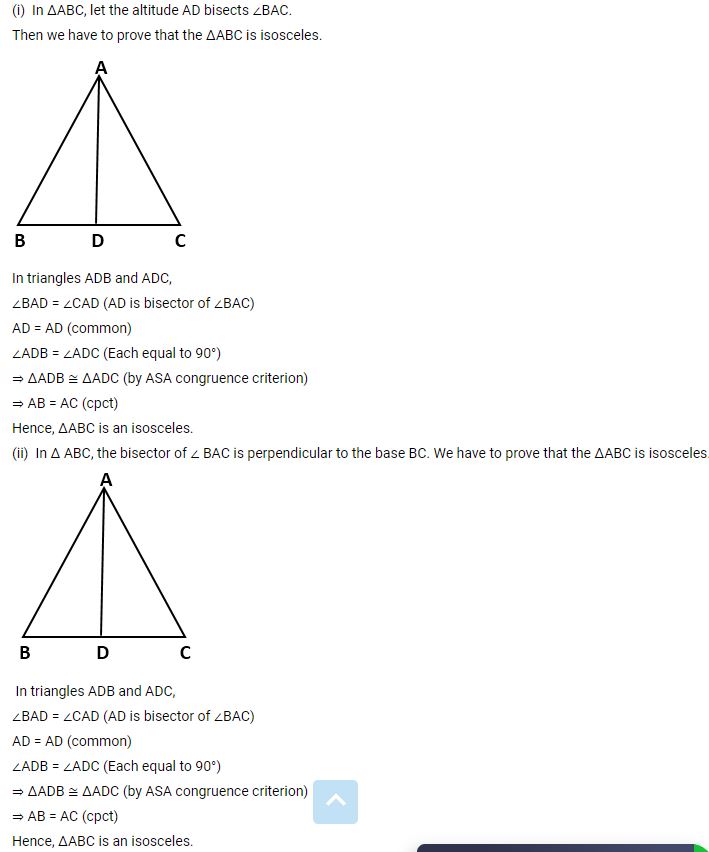
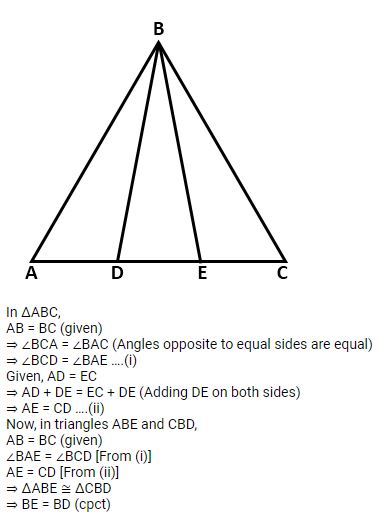
Question 20
In the given figure; AB = BC and AD = EC.
Prove that: BD = BE.
Answer
Selina ICSE Mathematics Solutions, Isosceles Triangles Concise Class-9th Exercise – 10 B
Question 1
If the equal sides of an isosceles triangle are produced, prove that the exterior angles so formed are obtuse and equal.
Answer


Question 2
In the given figure, AB = AC. Prove that:
(i) DP = DQ
(ii) AP = AQ
(iii) AD bisects angle A
Answer


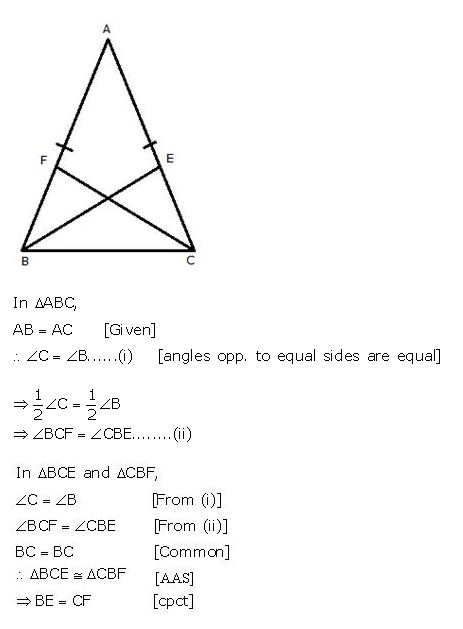
Question 3
In triangle ABC, AB = AC; BE……………… Prove that:
(i) BE = CF
(ii) AF = AE
Answer

Question 4
In isosceles triangle ABC, AB = AC. The side BA is produced to D such that BA = AD. Prove that: ∠BCD = 90o
Answer

Question 5
(i) In triangle ABC, AB = AC and = 36°. If the internal bisector of ∠C meets AB at point D, prove that AD = BC.
(ii) If the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
Answer
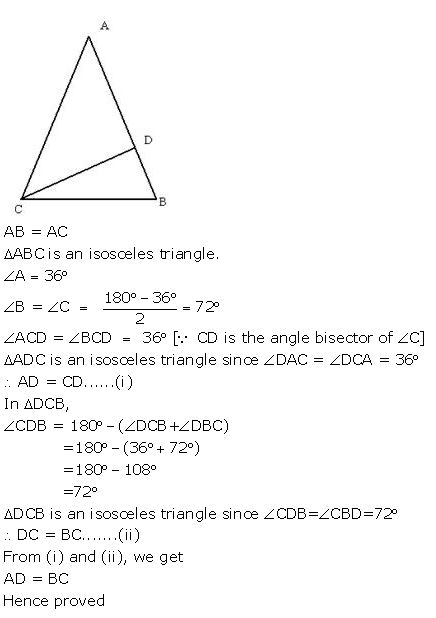
Question 6
Prove that the bisectors of the base angles of an isosceles triangle are equal.
Answer
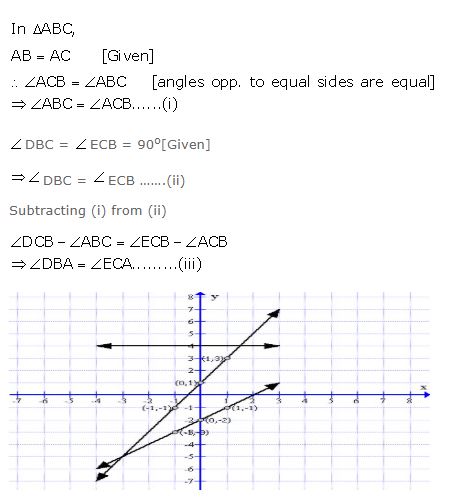
Question 7
In the given figure, AB = AC and ∠DBC = ∠ECB = 90o
Prove that:
(i) BD = CE
(ii) AD = AE
Answer
Question 8
ABC and DBC are two isosceles triangles on the same side of BC. Prove that:
(i) DA (or AD) produced bisects BC at right angle.
(ii) ∠BDA = ∠CDA.
Answer


Question 9
The bisectors of the equal angles B and C of an isosceles triangle ABC meet at O. Prove that AO bisects angle A.
Answer

Question 10
Prove that the medians corresponding to equal sides of an isosceles triangle are equal.
Answer
Question 11
Use the given figure to prove that, AB = AC.
Answer

Question 12
In the given figure; AE bisects exterior angle CAD and AE is parallel to BC.
Prove that: AB = AC.
Answer

Question 13
In an equilateral triangle ABC; points P, Q and R are taken on the sides AB, BC and CA respectively such that AP = BQ = CR. Prove that triangle PQR is equilateral.
Answer
Question 14
In triangle ABC, altitudes BE and CF are equal. Prove that the triangle is isosceles.
Answer
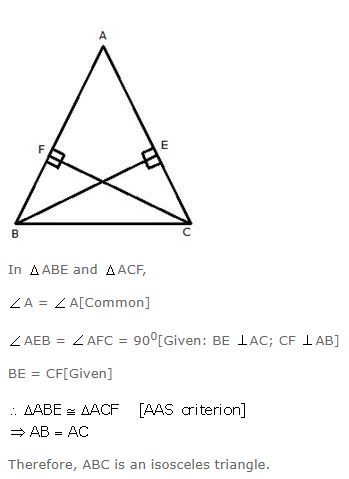
Question 15
Through any point in the bisector of angle, a straight line is drawn parallel to either arm of the angle. Prove that the triangle so formed is isosceles.
Answer

Question 16
In triangle ABC; AB = AC. P, Q and R are mid-points of sides AB, AC and BC respectively. Prove that:
(i) PR = QR(ii) BQ = CP
Answer
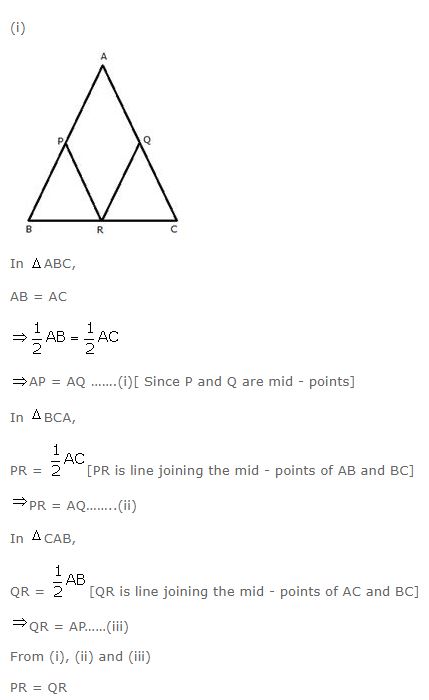
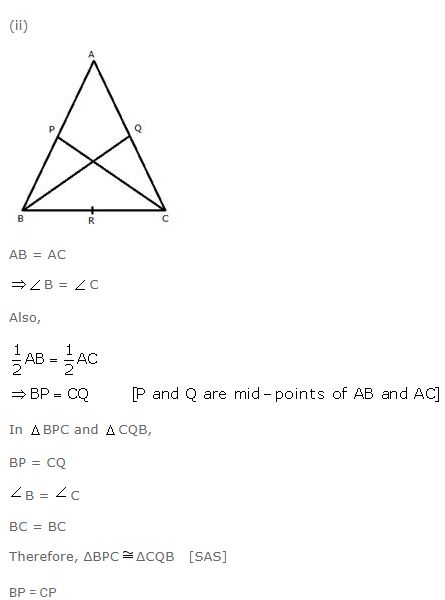
Question 17
From the following figure, prove that:
(i) ∠ACD = ∠CBE
(ii) AD = CE
Answer

Question 18
Equal sides AB and AC of an isosceles triangle ABC are produced. The bisectors of the exterior angle so formed meet at D. Prove that AD bisects angle A.
Answer


Question 19
ABC is a triangle. The bisector of the angle BCA meets AB in X. A point Y lies on CX such that AX = AY.
Prove that ∠CAY = ∠ABC.
Answer

Question 20
In the following figure; IA and IB are bisectors of angles CAB and CBA respectively. CP is parallel to IA and CQ is parallel to IB.
Prove that:
PQ = The perimeter of the ∇ABC.
Answer

Question 21
Sides AB and AC of a triangle ABC are equal. BC is produced through C upto a point D such that AC = CD. D and A are joined and produced upto point E. If angle BAE = 108o; find angle ADB.
Answer

Question 22
The given figure shows an equilateral triangle ABC with each side 15 cm. Also, DE//BC, DF//AC and EG//AB.
If DE + DF + EG = 20 cm, find FG.
Answer

Question 23
If all the three altitudes of a triangle are equal, the triangle is equilateral. Prove it.
Answer
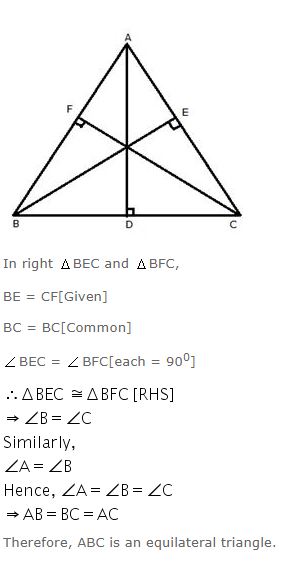
Question 24
In a ABC, the internal bisector of angle A meets opposite side BC at point D. Through vertex C, line CE is drawn parallel to DA which meets BA produced at point E. Show that ACE is ∇ isosceles.
Answer

Question 25
In triangle ABC, bisector of angle BAC meets opposite side BC at point D. If BD = CD, prove that ABC is ∇isosceles.
Answer
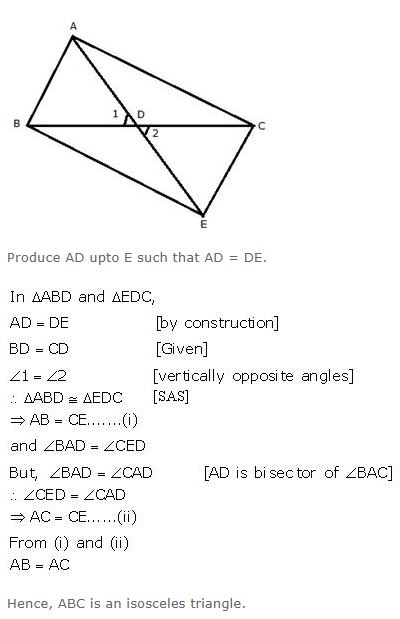
Question 26
In ∇ABC, D is point on BC such that AB = AD = BD = DC. Show that:
∠ADC: ∠C = 4: 1.
Answer

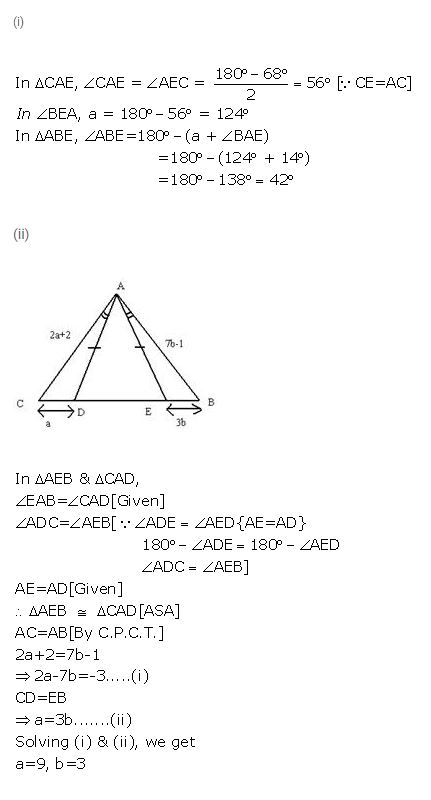
Question 27
Using the information given in each of the following figures, find the values of a and b.
[Given: CE = AC]
Answer
— End of Isosceles Triangles Concise Class-9th Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -9