Kinetic Theory of Gases Numerical Class-11 Nootan ISC Physics Ch-22 Behavior of Perfect Gas and Kinetic Theory of Gases. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-11 Physics.

Kinetic Theory of Gases Numerical Class-11 Nootan ISC Physics Ch-22 Behavior of Perfect Gas and Kinetic Theory of Gases
| Board | ISC |
| Class | 11 |
| Subject | Physics |
| Book | Nootan |
| Chapter-22 | Behavior of Perfect Gas and Kinetic Theory of Gases |
| Topics | Numericals on Kinetic Theory of Gases |
| Academic Session | 2025-2026 |
Numericals on Kinetic Theory of Gases
Class-11 Nootan ISC Physics Ch-22 Behavior of Perfect Gas and Kinetic Theory of Gases
Q-13. Kinetic energy of oxygen molecule at 0°C is 5.64 x 10^-21 J. Calculate Avogadro’s number.
Ans- K = 3RT/2N
=> N = 3RT/2K
=> 3 x 8.31 x 273 / 2 x 5.64 x 10^-21
=> 6.035 x 10^23
Q-14. The velocities of ten molecules of any gas are v , 0 , 2v , 4v , 3v , 2v , v , 3v , 5v , v. Calculate their root-mean- square (rms) velocity.
Ans-

Q-15. A flask of volume 1 x 10^-3 m³ contains 3.0 x 10^12 oxygen molecules at a certain temperature. The mass of one molecule of oxygen is 5.3 × 10^-26 kg and the root-mean-square velocity of its molecules at the same temperature is 400 m s^-1. Calculate the pressure of the oxygen gas in the flask.
Ans-
![]()
Q-16. A vessel is filled with oxygen gas (molecular weight 32) at 0°C temperature and at 1 atmospheric pressure. What is the root-mean-square speed of the oxygen molecules?
Ans-
Q-17. The mass of a molecule of krypton is 2.25 times the mass of a hydrogen molecule. A mixture of equal masses of these gas is enclosed in a vessel. Calculate at any constant temperature the ratio of the root- mean-square velocities of the molecules of krypton and hydrogen gases.
Ans-

Q-18. The density of a gas at normal pressure and 0°C temperature is 1.2 kg m^-3. Calculate: (i) the root- mean-square velocity of the molecules of the gas at 0°C, (ii) the temperature at which the velocity will become three times the initial velocity. (Normal pressure = 1.0 x 10^5 N m^-2).
Ans-

Q-19. The root-mean-square velocity of helium atoms at normal temperature and pressure is 1300 m s^-1. Calculate: (i) density of helium at 0°C, (ii) mass of the helium atom. (Normal pressure = 1.01 × 10^5 N m^-2).
Ans-
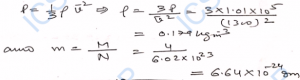
Q-20. The density of hydrogen at normal temperature and pressure is 0.09 kg m^-3. What will be the root-mean- square speed of its molecules ? What of oxygen? Oxygen is 16 times heavier than hydrogen.
Ans-
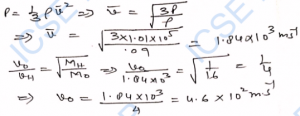
Q-21. The root-mean-square speed of oxygen molecules at a certain temperature is 150 m s^-1. Calculate the root-mean-square speed of hydrogen molecules at the same temperature. Molecular weights of oxygen and hydrogen are respectively 32 and 2.
Ans-

Q-22. What will be the ratio of the root-mean-square speeds of the molecules of an ideal gas at 270 K and 30 K ?
Ans-
![]()
Q-23. At what temperature will the root-mean-square velocity of molecules of a gas be twice the root-mean- square velocity at 0°C? At what temperature 1.5 times ?
Ans-

Q-24. At what temperature will the effective speed (root- mean-square speed) of oxygen molecule be equal to the effective speed of nitrogen molecule at 0°C ?
Ans-

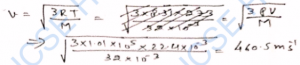
Q-25. The root-mean-square speed of oxygen molecules at 0°C is 460 m s^-1. What will be the speed of helium molecules at 40°C ? Molecular weight of oxygen is 32 g mol^-1 while that of helium is 4 g mol^-1
Ans-
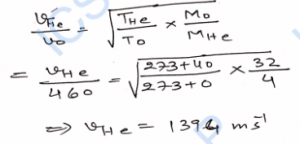
Q-26. At what temperature the kinetic energy of a molecule will be equal to 2.8 x 10^-20 J? Boltzmann constant (k) = 1.4 x 10^-23 J K^-1
Ans-
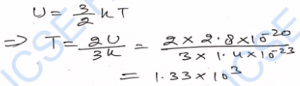
Q-27. The temperature of a gas is 0°C. In each case to what temperature should it be heated so that (i) the average kinetic energy of its molecule is doubled, (ii) the root- mean-square velocity of its molecules is doubled?
Ans-
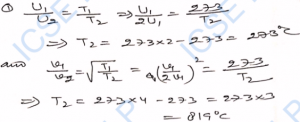
Q-28. If the kinetic energy of 1 mole of a gas at 27°C is 3400 J, what will be its value at 327°C ?
Ans-
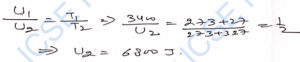
Q-29. The mean kinetic energy of 1 kg-mol of nitrogen at 27°C is 600 J. What will be its mean kinetic energy at 127°C ?
Ans-
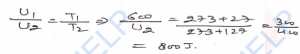
Q-30. The average kinetic energy of a hydrogen molecules at 27°C is 9.3 x 10^21 J. The mass of hydrogen molecule is 3.1 x 10^-27 kg. Determine (i) the average kinetic energy at 227°C, (ii) the root-mean-square speed of hydrogen molecule at 27°C.
Ans-
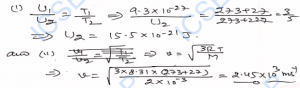
Q-31. At what temperature will the average value of the kinetic energy of the molecule of a gas be 1/3 of the average value of kinetic energy at 27°C ?
Ans-

Q-32. If the temperature of air is increased from 27°C to 227°C, in what ratio will the average kinetic energies of its molecules be increased ?
Ans-
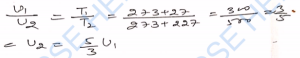
Q-33. The temperature of a gas is – 68°C. To what temperature should it be heated so that (i) the average kinetic energy of the molecules be doubled, (ii) the root-mean-square velocity of the molecules be doubled?
Ans-

Q-34. Up to what temperature should the hydrogen gas initially at 327°C be cooled so that the root-mean- square velocity of its molecules becomes half of its initial value ? The pressure remains constant.
Ans- -123°
Q-35. There are 6 x 10^21 hydrogen molecules in a vessel of volume 200 cm³. Its temperature is 27°C and the pressure is 10^5 N m^-2. If the temperature be raised to 47°C, then in what ratio the following quantities would change: (i) number of molecules per unit volume, (ii) pressure of the gas in the vessel, (iii) average kinetic energy of hydrogen ?
Ans-

Q-36. Calculate for hydrogen (molecular-weight = 2) at 27°C: (i) kinetic energy of one mole of the gas, (ii) kinetic energy of one gram gas, (iii) root-mean- square velocity of the molecules.
Ans-

Q-37. Find the average kinetic energy of a gas molecule of (i) monoatomic gas, (ii) diatomic gas at 20°C. k = 1.38 × 10^-23 J mol^-1 K^-1.
Ans-

— : End of Kinetic Theory of Gases Numerical Class-11 Nootan ISC Physics Ch-22 Behavior of Perfect Gas and Kinetic Theory of Gases.. :–
Return to : – – Nootan Solutions for ISC Physics Class-11
Thanks
Please share with your friends