Lens Maker’s Formula Numerical Class-12 Nootan ISC Physics Solution Ch-16 Refraction of Light at Spherical Surfaces : Lenses. Step by step solutions of Kumar and Mittal Physics of Nageen Prakashan as council latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ISC Board Class-12 Physics.

Lens Maker’s Formula Numerical Class-12 Nootan ISC Physics Solution Ch-16 Refraction of Light at Spherical Surfaces : Lenses
| Board | ISC |
| Class | 12 |
| Subject | Physics |
| Book | Nootan |
| Chapter-16 | Refraction of Light at Spherical Surfaces : Lenses |
| Topics | Numericals on Lens Maker’s Formula |
| Academic Session | 2025-2026 |
Numericals on Lens Maker’s Formula
Class-12 Nootan ISC Physics Solution Ch-16 Refraction of Light at Spherical Surfaces : Lenses
Que-11. A ray of light falls on a transparent sphere of n = √3 at an angle of incidence 60° with the diameter AB of the sphere having centre C. The ray emerges out from the sphere parallel to the line BD. Find the angle of emergence.
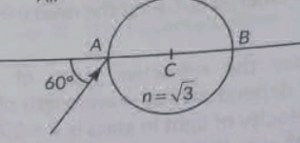
Ans- Refraction at Entry: Using Snell’s law, the angle of refraction inside the sphere is 30°.
Geometry: Due to the sphere’s symmetry, the angle of incidence at the exit point is also 30°.
Refraction at Exit: Applying Snell’s law again, the angle of emergence is 60°.
Que-12. The radii of curvature of a double convex lens are 15 cm and 30 cm and the refractive index of its glass is 1.5. Calculate the focal length of the lens.
Ans- 1/f = (1μ2 – 1) (1/R1 + 1/R2)
=> 1/f = (1.5 – 1) {1/15 + 1/30}
=> f = 20 cm
Que-13. The radii of curvature of a double concave lens are 30 cm and 60 cm and the refractive index of its glass is 1.5. Calculate the focal length of the lens.
Ans- 1/f = -(1μ2 – 1) (1/R1 + 1/R2)
=> 1/f = -(1.5 – 1) {1/30 + 1/60}
=> f = -40 cm
Que-14. The radius of curvature of each face of a biconcave lens made of glass of refractive index 1.5 is 30 cm. Calculate the focal length of the lens in air.
Ans- 1/f = -(1μ2 – 1) (1/R1 + 1/R2)
=> 1/f = -(1.5 – 1) {1/30 + 1/30}
=> f = -30 cm
Que-15. The radius of curvature of the convex face of a plano-convex lens is 55 cm and the refractive index of its material is 1.55. Find the focal length of the lens.
Ans- 1/f = (1μ2 – 1) (1/R1 + 1/∞) plano convex
=> 1/f = (1.55 – 1) {1/55}
=> f = 100 cm
Que-16. The radii of curvature of the two faces of a convex lens are 0.10 m and 0.15 m respectively. If the focal length of the lens is 0.12 m, find the refractive index of the material of the lens.
Ans- 1/f = (1μ2 – 1) (1/R1 + 1/R2)
=> 1/0.12 = (1μ2 – 1) {1/0.10 + 1/0.15}
=> 1μ2 – 1 = 0.5
=> 1μ2 = 1.5
Que-17. The radii of curvature of the two surfaces of a convexo-concave lens are 15 cm and 30 cm. Find the focal length 1 of the lens. Take refractive index of the lens material to be 1.5.
Ans- In case of convexo concave both radius is negative
∴ 1/f = (1μ2 – 1) (-1/R1 + 1/R2)
=> 1/f = (1.5 – 1) {-1/15 + 1/30}
=> f = 60 cm
Que-18. (a) A bi-convex spherical lens has a focal length of 20 cm. If it is split along a plane AB into two halves to form two plano-convex lenses, then what will be the focal length of each plano-convex lens? (b)What if the lens be cut along CD?

Ans- (a) In this type of situation the power of the lens will be half and focus will be doubled
i.e. new focus = 40 cm.
(b) In this situation focus and power will be same but amount of light entering the lens will be reduced.
Que-19. The radii of curvature of a convexo-convex lens of glass (n = 1.50) are in the ratio 1: 2. This lens renders the rays coming from an illuminated filament at a distance of 6.0 cm parallel. Calculate the radii of curvature of its surfaces.
Ans- R1:R2 = 1:2 => R:2R (let)
now 1/f = (1.5 – 1) {1/R + 1/2R}
=> 0.5{3/2R} = 1/6
=> R = 4.5 cm
∴R2 = 9.0 cm
— : End of Lens Maker’s Formula Numerical Class-12 Nootan ISC Physics Solution Ch-16. :–
Return to : – Nootan Solutions for ISC Class-12 Physics
Thanks
Please share with your friends


