Linear Inequations Class 10 RS Aggarwal MCQs Goyal Brothers ICSE Maths Solutions Ch-4. Step by step solutions of MCQs questions with hints as latest prescribe guideline for upcoming exam. Visit official Website CISCE for detail information about ICSE Board Class-10.

Linear Inequations Class 10 RS Aggarwal MCQs Goyal Brothers ICSE Maths Solutions Ch-4
| Board | ICSE |
| Subject | Maths |
| Class | 10th |
| Chapter-4 | Linear Inequations |
| Writer/Book | RS Aggarwal |
| Topics | Solution of Exe-4 MCQs |
| Academic Session | 2024-2025 |
Multiple Choice Questions on Inequality
(Linear Inequations Class 10 RS Aggarwal MCQs Goyal Brothers ICSE Maths Solutions Ch-4)
Page- 42,43
Que-1: Which of the following is not a linear inequation?
(a) 3x-8 > 5+2x (b) (5x/2)-3 ≤ (9x/4)+12 (c) 4x-7/3 ≥ 13x+8 (d) 6x+13 < 4/x – 3
Solution- (d) 6x+13 < 4/x – 3
Reason: as x is in denominator
Que-2: Which of the following is a linear inequation?
(a) x²+3 ≥ 2x-7 (b) 7/(x-1) < 3x+4 (c) (7x/3)-9 ≤ 5+(4x/7) (d) 5-(9/x) > 3x+4
Solution- (c) (7x/3)-9 ≤ 5+(4x/7)
Reason: Others are either in squire form or x is in denominator
Que-3: Which of the following is not a general form of linear inequation?
(a) ax+b > c (b) (a/x)+b ≥ c (c) ax+b ≤ c (d) ax²+b < c
Solution- (d) ax²+b < c
Reason: variable is in squire form
Que-4: Which of the following is reducible to a linear inequation?
(a) 7-x² ≤ 5x+3 (b) (3/x)-8 > 4 (c) 4-(2/x) ≥ (1/x²)-6 (d) 11-x ≤ 5x²+6
Solution- (b) (3/x)-8 > 4
Reason:
Que-5: Which of the following is not reducible to a linear inequation?
(a) 3-(7/x) < 5 (b) 8+(3/x) ≥ (5/x)-4 (c) (6/x)-8 > (4/x)+3x (d) 3/(x-1)-7 < 9
Solution- (c) (6/x)-8 > (4/x)+3x
Reason: on solving (c) it becomes quadratic form
Que-6: Which of the following is not true for the linear inequations?
(a) Adding the same number to each side of an inequation does not change the inequality.
(b) Multiplying each side of an inequation by the same positive number reverses the inequality.
(c) Multiplying each side of an inequation by the same negative number reverses the inequality.
(d) Dividing each side of an inequation by the same positive number does not change the inequality.
Solution- not true option is (b) Multiplying each side of an inequation by the same positive number reverses the inequality.
Reason: Multiplying / dividing each side of an inequation by the same positive number No change in the inequality sign. Only change if Mul / Div. by negative number
Que-7: Which of the following is not true?
(a) p>q ⇔ q>p (b) p<q ⇔ q>p (c) p≥q ⇔ q≤p (d) p≤q ⇔ q≥p
Solution- (a) p>q ⇔ q>p
Reason: in LHS P is greater while in RHS P is smaller Hence it is not possible
Que-8: Which of the following is the solution set of x≤7, when the replacement set is the set of natural numbers?
(a) {1,2,3,4,5,6,7} (b) {0,1,2,3,4,5,6,7} (c) {1,2,3,4,5,6} (d) {0,1,2,3,4,5,6}
Solution- (a) {1,2,3,4,5,6,7}
Reason: because sign ≤ indicate not only smaller but also equal hence 7 is also added in solution set of (a) while (b) contain 0 which is not natural number set
Que-9: Which of the following is the solution set of x<0, when the replacement set is the set of whole number?
(a) {0} (b) {…….,-3,-2,-1} (c) {…….,-3,-2,-1,0,} (d) Null set
Solution- (d) Null set
Reason: as x is whole number so the least value is 0 and there is no number less than 0 in whole number
Que-10: Which of the following is the solution set of x≤3, when the replacement set is the set of integers?
(a) {0,1,2,3} (b) {…,-2,-1,0,1,2} (c) {…,-2,-1,0,1,2,3} (d) {…,-2,-1,1,2,3}
Solution- (c) {….,-2,-1,0,1,2,3}
Reason: as x is integer so all negative number, zero and up to 3 positive number may be solution set
Que-11: Which of the following statements is not true? (r is a positive integer)
(a If p<q, then p-r < q-r (b) If p ≥ q, then -pr ≥-qr (c) If p>q, then (p/r)>(q/r) (d) If p≤q, then p+r ≤ q+r
Solution- (b) If p≥q, then -pr ≥-qr
Reason: on multiplying both side negative number sign must be reverse here – r is multiplying both side without sign change hence it is not true
Que-12: Which of the following statements is true?(r is a positive integer)
(a) If p≥q, then (-p/r) ≤ (-q/r) (b) If p≤q, then pr ≥ qr (c) If p>q, then -pr > -qr (d) If p<q, then p-r < q-r
Solution- (a) If p≥q, then (-p/r) ≤ (-q/r)
Reason: on multiplying both side negative number sign must be reverse
Que-13: Graphical representation of the following inequation on the number line is {x : -3 < x < 2, x ∈ I}
(a) … , (b) ….., (c) ….. , (d)
Solution- (c)
Reason: as solution set are -2, -1, 0 , 1 in this case -3 < x < 2, x ∈ I
Que-14: Which of the following is the correct graphical representation of {x : x < 1, x ∈ I} on the number line?
(a) … , (b) ….., (c) ….. , (d)
Solution- (a)
Reason: Solution set are all negative, zero, these integers are less than 1
Que-15: Which of the following is the correct graphical representation of {x : -4 < x ≤ 2, x ∈ R} on the number line?
(a) … , (b) ….., (c) ….. , (d)
Solution- (c)
Reason: on solving given inequality the solutions set are – -3,-2, -1 ,0 ,1,2
Que-16: The solution set of 4x-3 ≤ 5, where x ∈ N, is :
(a) {1} (b) {1,2} (c) {0,1,3} (d) None of these
Solution- (b) {1,2}
Reason: Solve the inequation and choose only natural number among them
Que-17: The solution set of 3x+1 > 5x-7, where x ∈ R, is:
(a) {x : x < 4, x ∈ R} (b) {x : x > 4, x ∈ R} (c) {x : x < 8, x ∈ R} (d) {x : x > -4, x ∈ R}
Solution- (a) {x : x < 4, x ∈ R}
Reason: Solve the inequation and choose all number among them as it is real number
Que-18: The solution set of 4x-9 ≥ 7, where x ∈ {1,2,3,4,5,6,7,8}, is :
(a) {1,2,3,4} (b) {4,5,6,7,8} (c) {1,2,3} (d) {5,6,7,8}
Solution- (b) {4,5,6,7,8}
Reason: 4x-9+9 ≥ 7 +9,
4x ≥ 16,
x ≥ 16/4,
x ≥ 4,
Que-19: Find the values of x in the inequation 3x-2 > 9x-16, where x ∈ I.
(a) {-2,-1,0,1,2} (b) {2,3,4,5,…} (c) {…..,-2,-1,0,1,2} (d) {…..,-2,-1,0,1,2,3}
Solution- (c) {…..,-2,-1,0,1,2}
Reason: Solve the inequation
Que-20: The largest value of x for which 3(x-2) ≤ 6-x, where x ∈ W, is :
(a) 3 (b) 4 (c) 6 (d) None of these
Solution- (c) 6
Reason:
Que-21: If x is a negative integer, then find the solution set of 3+2(x+1) > -1
(a) {-3,-2,-1} (b) {-2,-1} (c) {-1} (d) none of these
Solution- (b) {-2,-1}
Reason:
Que-22: Find the smallest value of x in the following inequation.
3(x+4) ≤ 5(x-1) + 4 and x ≤ N
(a) 5 (b) 6 (c) 7 (d) 8
Solution- (c) 7
Reason:
Que-23: What is the smallest value of x in the following inequation ? 20-5x < 5(x+8) and x ∈ I
(a) -1 (b) 1 (c) 0 (d) cannot be determined
Solution- (a) -1
Reason:
Que-24: What is the solution set for the inequation represented by the following number line ?
(a) {x ∈ R : -3 < x ≤ 4} (b) {x ∈ R : -3 < x < 4} (c) {x ∈ R : -3 ≤ x < 4}
(d) {x ∈ R :
Solution- (a) {x ∈ R : -3 < x ≤ 4}
Reason:
Que-25: The solution set of the inequation x-3 ≥ -5, x ∈ R is :
(a) {x : x > -2, x ∈ R} (b) {x : x ≤ -2, x ∈ R} (c) {x : x ≥ -2, x ∈ R} (d) {-2,-1,0,1,2}
Solution- (c) {x : x ≥ -2, x ∈ R}
Reason:
Que-26: Find the greatest integer which is such that if 7 is added to its double, then the resulting number is greater than three times the integer.
(a) 7 (b) 8 (c) 6 (d) none of these
Solution- (c) 6
Reason:
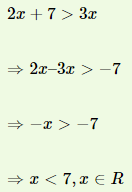
Que-27: The solution set for the inequation 2x+4 ≤ 14, x ∈ W is :
(a) {1,2,3,4,5} (b) {0,1,2,3,4,5} (c) {1,2,3,4} (d) {0,1,2,3,4}
Solution- (b) {0,1,2,3,4,5}
Reason:
— : End of Linear Inequations Class 10 RS Aggarwal MCQs Goyal Brothers ICSE Maths Solutions :—
Return to :– RS Aggarwal ICSE Class 10 Solutions Goyal Brothers
Thanks
Please, Share with your friends


