Linear Inequations ICSE Class-8th Concise Selina Maths

Linear Inequations ICSE Class-8th Concise Mathematics Selina Solutions Chapter-15 . We provide step by step Solutions of Exercise / lesson-15 Linear Inequations  for ICSE Class-8 Concise Selina Mathematics. Our Solutions contain all type Questions with Exe-15 A    and Exe-15 B to develop skill and confidence . Visit official Website CISCE for detail information about ICSE Board Class-8.

Linear Inequations ICSE Class-8th Concise Maths Selina Solutions Chapter-15

---

–: Select Topics :–

 

Exe-15 A,

Exe-15 B,

---

Exercise – 15 A of Linear Inequations Solved Questions for ICSE Class-8th Mathematics Concise Selina Publications

Question 1.

If the replacement set is the set of natural numbers, solve.
(i) x – 5 < 0
(ii) x + 1 < 7
(iii) 3x – 4 > 6
(iv) 4x + 1 > 17
Answer

(i)

x – 5 < 0

x – 5 + 5 <0 + 5 ………(Adding 5)

=> x < 5

Required answer = {1, 2, 3, 4}

(ii)

x + 1 ≤ 7

⇒ x + 1 – 1 ≤ 7 – 1 (Subtracting 1)

⇒ x ≤ 6

Required answer = {1, 2, 3, 4, 5, 6}

(iii)

3x – 4 > 6

3x – 4 + 4 > 6 + 4 (Adding 4)

⇒ 3x > 10

3x/3 > 10 3  …(Dividing by 3)

⇒ x > 10/3

⇒ x > 3 (1/3)

Required answer = { 4, 5, 6, …}

(iv)

4x + 1 ≥ 17

⇒ 4x + 1 – 1 ≥ 17 – 1  (Subtracting)

⇒ 4x ≥ 16

⇒ 4x/4 ≥ 16/4 (Dividing by 4)

⇒ x ≥ 4

Required answer = {4, 5, 6, …}

Question 2.

If the replacement set = {-6, -3, 0, 3, 6, 9}; find the truth set of the following:
(i) 2x – 1 > 9
(ii) 3x + 7 < 1

Answer

(i)

2x – 1 > 9

⇒ 2x – 1 + 1 > 9 + 1 (Adding 1)

⇒ 2x > 10

⇒ x > 5 (Dividing by 2)

⇒ x > 5

Required answer = {6, 9}

(ii)

3x + 7 ≤ 1

⇒ 3x + 7 – 7 ≤ 1 – 7 (Subtracting 7)

⇒ 3x ≤ – 6

⇒ x ≤ – 2

Required Answer = {-6, -3}

Question 3.

Solve 7 > 3x – 8; x ∈ N
Answer

> 3x – 8

⇒ 7 – 3x > 3x – 3x – 8 (Subtracting 3x)

⇒ 7 – 7 – 3x > 3x – 3x – 8 – 7 (Subtracting 7)

⇒ -3x > -15

⇒ x < 5 (Dividing by -3)

Required Answer = {1, 2, 3, 4}

Question 4.

-17 < 9y – 8 ; y ∈ Z
Answer

-17 < 9y – 8

⇒ -17 + 8 < 9y – 8 + 8 (Adding 8)

⇒ -9 < 9y

⇒ -1 < y (Dividing by 9)

Required number = {0, 1, 2, 3, 4, …}

Question 5.

Solve 9x – 7 ≤ 28 + 4x; x ∈ W
Answer

9x – 1 ≤ 28 + 4x

⇒ 9x – 4x – 7 ≤ 28 + 4x – 4x (Subtracting 4x)

⇒ 5x – 7 ≤ 28

⇒ 5x – 7 + 7 ≤ 28 + 7 (Adding 7)

⇒ 5x ≤ 35

⇒ x ≤ 7 (Dividing by 5)

Required answer = {0, 1, 2, 3, 4, 5, 6, 7}

Question 6.

Solve : x + 8 < 12 ; x ∈ W
Answer

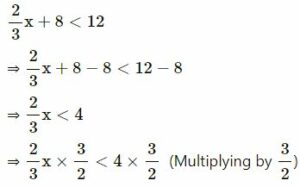
⇒ x < 6

∴ Required answer = {0, 1, 2, 3, 4, 5}

Question 7.

Solve -5 (x + 4) > 30 ; x ∈ Z
Answer

-5 (x + 4) > 30

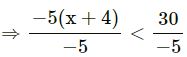
..(Dividing by -5)

Note: Division by a negative number reverses the equality.

⇒ x + 4 < -6

⇒ x + 4 – 4 < – 6 – 4  …(Subtracting 4)

⇒ x < -10

∴ Required answer = {-11, -12, -13, …}

Question 8.

Solve the inequation 8 – 2x > x – 5 ; x ∈ N.
Answer

8 – 2x ≥ x – 5; x ∈ N.

⇒ 8 + 5 ≥ 2x + x

⇒ 13 ≥ 3x ⇒ 3x ≤ 13

⇒ x ≤ 13/3 = 4 (1/3)

x = 1, 2, 3, 4 (x ∈ N)

Solution set = {1, 2, 3, 4}

Question 9.

Solve the inequality 18 – 3 (2x – 5) > 12; x ∈ W.
Answer

18 – 3 (2x – 5) > 12; x ∈ W.

⇒ 18 – 6x + 15 > 12

⇒ 33 – 12 > 6x

⇒ 21 > 6x

⇒ 6x < 21

⇒ x < (21/6)+ (7/2) = 3 (1/2)

But x ∈ W, x = 0, 1, 2, 3

∴ Solution set = {0, 1, 2, 3}

Question 10.

Solve :  + 15 < 17; x ∈ W.
Answer

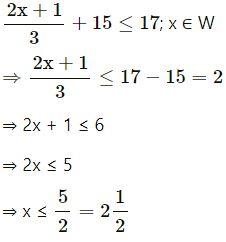
But x ∈ W

∴ x = 0, 1, 2

∴ Solution set is = {0, 1, 2}

Question 11.

Solve : -3 + x < 2, x ∈ N
Answer

-3 + x < 2, x ∈ N.

⇒ x < 2 – (-3)

⇒ x < 2 + 3

⇒ x < 5

∴ x = 1, 2, 3, 4   (∵ x ∈ N)

∴ Solution set = {1, 2, 3, 4}

Question 12.

Solve : 4x – 5 > 10 – x, x ∈ {0, 1, 2, 3, 4, 5, 6, 7}
Answer

4x – 5 > 10 – x, x ∈ N.

⇒ 4x + x > 10 + 5

⇒ 5x > 15

⇒ x > 15/5 = 3

∴ x = 4, 5, 6, 7

Solution set = {4, 5, 6, 7}

Question 13.

Solve : 15 – 2(2x – 1) < 15, x ∈ Z.
Answer

15 – 2(2x – 1) < 15, x ∈ Z.

⇒ 15 – 4x + 2 < 15

⇒ 17 – 4x < 15

⇒ – 4x < 15 – 17

⇒ – 4x < -2

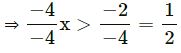
(Dividing by -4)

∴ x = 1, 2, 3, 4, 5, …..

∴ Solution set = {1, 2, 3, 4, 5,…}

Question 14.

Solve :  >  , x ∈ W.
Answer

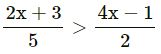
⇒ 2(2x + 3) > 5(4x – 1)

⇒ 4x + 6 > 20x – 5

⇒ 4x – 20x > – 5 – 6

⇒ -16x > -11

⇒ x < (-11/-16)   (Dividing by -16)

⇒ x < (11/16)

∴ x = 0

∴ Solution set = {0}

---

Selina Solutions – Linear Inequations, Exe-15 B for ICSE Class-8th  Mathematics 

Solve and graph the solution set on a number line :

Question 1.

x – 5 < -2 ; x ∈ N
Answer

x – 5 < -2

⇒ x – 5 + 5 < – 2 + 5    (Adding 5 to both sides)

⇒ x < 3

So required graph is:

Question 2.

3x – 1 > 5 ; x ∈ W
Answer

3x – 1 > 5

⇒ 3x – 1 + 1 > 5 + 1 (Adding 1 to both sides)

⇒ 3x > 6

⇒ 3x/3 > 6/3  (Dividing both sides by 3)

⇒ x > 2

So required graph is:

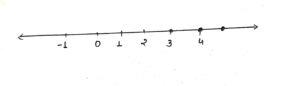
Question 3.

-3x + 12 < -15 ; x ∈ R.
Answer

3x + 12 < -15

⇒ -3x + 12 – 12 < – 15 -12  (Subtracting 12 from both sides)

⇒ -3x < -27

⇒ -3x-3>-27-3  (Dividing both sides by -3)

⇒ x > 9

So required graph is:

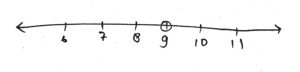
Question 4.

7 > 3x – 8 ; x ∈ W
Answer

7 ≥ 3x – 8

⇒ 7 + 8 ≥ 3x – 8  8  (Adding 8 to both sides)

⇒ 15 ≥ 3x

⇒ (15/3) ≥ (3x/3)  (Dividing both sides by 3)

⇒ 5 ≥ x

So required graph is:

Question 5.

8x – 8 < – 24 ; x ∈ Z
Answer

8x – 8 ≤ – 24

⇒ 8x – 8 + 8 ≤ – 24 + 8  ..(Adding 8 to both sides)

⇒ 8x ≤ -16

⇒ (8x/8) ≤ (-16/8)

..(Dividing both sides by 8)

⇒ x ≤ -2

So required graph is:

Question 6.

8x – 9 > 35 – 3x ; x ∈ N
Answer

8x – 9 ≥ 35 – 3x

⇒ 8x + 3x – 9 ≥ 35 – 3x + 3x   …(Adding 3x to both sides)

⇒ 11x – 9 ≥ 35

⇒ 11x – 9 + 9 ≥ 35 + 9  ..(Adding 9 to both sides)

⇒ 11x ≥ 44

⇒ (11x/11) ≥ (44/11)  …(Dividing both side by 11)

⇒ x ≥ 4

So required graph is:

Question 7.

5x + 4 > 8x – 11 ; x ∈ Z
Answer

5x + 4 > 8x – 11

⇒ 5x – 5x + 4 > 8x – 5x – 11 ..(Subtracting 5x from both sides)

⇒ 4 > 3x – 11

⇒ 4 + 11 > 3x – 11 + 11  …(Adding 11 to both sides)

⇒ 15 > 3x

⇒ 15/3 > 3x/3

…(Dividing both sides by 3)

⇒ 5 > x

So required graph is:

Question 8.

 + 1 < -3 ; x ∈ R
Answer

(2x/5) +1<-3

⇒ (2x/5) +1-1<-3-1  (Subtracting 1 from both sides)

⇒ (2x/5)<-4

⇒ (2x/5)×5<-4×5  …(Multiplying both sides by 5)

⇒ 2x < – 20

⇒ (2x/2)<(-20/2)  …(Dividing both sides by 2)

⇒ x < -10

So required graph is:

Question 9.

 > -1 +  ; x ∈ N
Answer

x/2 > -1+ (3x/4)

⇒ x/2 × 4 > -1 × 4 + (3x/4) × 4  ..(Multiplying both sides by 4)

⇒ 2x > -4 + 3x

⇒ 2x – 2x > – 4 + 3x – 2x  …(Subtracting 2x from both sides)

⇒ 0 > – 4 + x

⇒ 0 + 4 > – 4 + 4 + x  …(Adding 4 to both sides)

⇒ 4 > x

So required graph is:

Question 10.

 x + 5 ≤  x + 6 ; x ∈ W
Answer

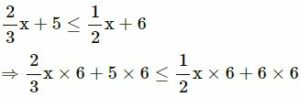
….(Multiplying both sides by 6)

⇒ 4x + 30 ≤ 3x + 36

⇒ 4x – 3x + 30 ≤ 3x – 3x + 36  …(Substracting 3x from both sides)

⇒ x + 30 ≤ 36

⇒ x + 30 – 30 ≤ 36 – 30    …(Substracting 30 from both sides)

x ≤ 6

So required graph is:

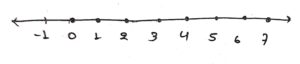
Question 11.

Solve the inequation 5(x – 2) > 4 (x + 3) – 24 and represent its solution on a number line.
Given the replacement set is {-4, -3, -2, -1, 0, 1, 2, 3, 4}.
Answer

5(x – 2) > 4 (x + 3) – 24

⇒ 5x – 10 > 4x + 12 – 24

⇒ 5x – 4x > 10 – 12

⇒ x > -2

Since replacement set ={-4, -3, -2, -1, 0, 1, 2, 3, 4}

∴ Solution set = {-1, 0, 1, 2, 3, 4}

So required graph is:

Question 12.

Solve  (x – 1) + 4 < 10 and represent its solution on a number line.
Given replacement set is {-8, -6, -4, 3, 6, 8, 12}.
Answer

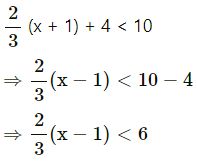
⇒ 2(x – 1) < 18

⇒ x – 1 < 9

⇒ x – 1 + 1 < 9 + 1  ….(Adding 1 to both sides)

⇒ x < 10

Question 13.

For each inequation, given below, represent the solution on a number line :
(i)  – 2x ≥  ; x ∈ W
(ii) 3(2x – 1) ≥ 2(2x + 3), x ∈ Z
(iii) 2(4 – 3x) ≤ 4(x – 5), x ∈ W
(iv) 4(3x + 1) > 2(4x – 1), x is a negative integer
(v)  < 3, x ∈ R
(vi) -2(x + 8) ≤ 8, x ∈ R
Answer

(i)

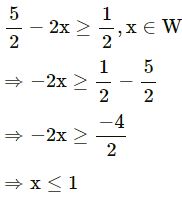
∴ x = {0, 1}

(ii)

3(2x -1) ≥ 2(2x + 3), x ∈ Z

⇒ 6x – 3 ≥ 4x + 6, x ∈ Z

⇒ 6x – 4x ≥ 6 + 3

⇒ 2x ≥ 9

⇒ x ≥ 9/2

⇒ x ≥ 4 (1/2)

∴ x = {5, 6, 7, ….}

(iii)

2(4 – 3x) ≤ 4(x – 5), x ∈ W

8 – 6x ≤ – 20 – 8

⇒ -6x – 4x ≤ – 20 – 8

⇒ -10x ≤ – 28

⇒  10x ≥ 28

⇒ x ≥ 28/10

⇒ x ≥ 2.8

∴ x = {3, 4, 5, ….}

(iv)

4(3x + 1) > 2(4x – 1), x is a negative integer

⇒ 12x + 4 > 8x – 2

⇒ 12x – 8x > -2 – 4

⇒ 4x > -6

⇒ x > -64

⇒ x > -1.5

∴ x = {-1}

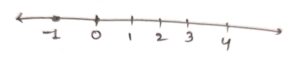
(v)

(4-x/2) <3 , x ∈ R

⇒ 4 – x < 6

⇒ – x < 6 – 4

⇒ – x < 2

⇒ x > -2

∴ x > – 2

(vi)

-2(x + 8) ≤ 8, x ∈ R

– 2x – 16 ≤ 8

⇒ – 2x ≤ 8 + 16

⇒ – 2x ≤ 24

⇒ x ≥ -24/2

x ≥ -12

— End of Linear Inequations Solutions :–

Return to – Concise Selina Maths Solutions for ICSE Class -8 

---