Lines and Angles ICSE Class-7th Concise Selina Mathematics

Lines and Angles ICSE Class-7th Concise Selina Mathematics Chapter-14 . We provide step by step Solutions of Exercise / lesson-14 Lines and Angles (Including Construction of angles)  for  ICSE Class-7 Concise Selina Mathematics. Our Solutions contain all type Questions with Exe-14 A , Exe-14 B,  and  Exe-14 C to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-7.

Lines and Angles ICSE Class-7th Concise Selina Mathematics Chapter-14

(Including Construction of angles)

---

–: Select Topics :–

 

Exe-14 A,

Exe-14 B,

Exe-14 C,

 

---

Exercise – 14 A Lines and Angles ICSE Class-7th Concise Selina Mathematics

Question 1.

State, true or false :
(i) A line segment 4 cm long can have only 2000 points in it.
(ii) A ray has one end point and a line segment has two end-points.

(iii) A line segment is the shortest distance between any two given points.
(iv) An infinite number of straight lines can be drawn through a given point.
(v) Write the number of end points in
(a) a line segment AB (b) arayAB
(c) a lineAB
(vi) Out of  ,  ,  and  , which one has a fixed length?
(vii) How many rays can be drawn through a fixed point O?
(viii) How many lines can be drawn through three
(a) collinear points?
(b) non-collinear points?
(ix) Is 40° the complement of 60°?
(x) Is 45° the supplement of 45°?

Answer

(i) False. It has an infinite number of points.

(ii) True

(iii) True

(iv) True

(v) (a) 2 (b) 1 (c) 0

(vi) AB

(vii) Infinite

(viii) (a) 1 (b) 3

(ix) False. 40° is the complement of 50° as 40° + 50° = 90°

(x) False. 45° is the supplement of 135°, not 45°.

Question 2.

In which of the following figures, are ∠AOB and ∠AOC adjacent angles? Give, in each case, reason for your answer.

Answer

Question 3.

In the given figure, B AC is a straight line.
Find : (i) x (ii) ∠AOB (iii) ∠BOC

Answer

∵ ∠AOB and ∠COB are linear pairs

so ∠AOB + ∠COB = 180°

⇒ x + 25° + 3x + 15° = 180°

⇒ 4x + 40° = 180°

⇒ 4x = 180°− 40°

= 140°

(i) ⇒ x =140°/4

=35°

Hence, x = 35°

(ii) ∠AOB = x + 25°

= 35° + 25° = 60°

(iii) ∠BOC = 3x + 15°

= 3 × 35° + 15°
= 105° + 15°

= 120°

Question 4.

Find yin the given figure.

Answer

∵ AOC is a straight line

so ∠AOB + ∠BOD + ∠DOC

= 180°

⇒ y + 150°− x + x

= 180°

⇒ y + 150° = 180°

⇒ y = 180°− 150°

= 30°

Hence,

y = 30°

Question 5.

In the given figure, find ∠PQR.

Answer

SQR is a straight line

so ∠SQT + ∠TQP + ∠PQR

= 180°

⇒ x + 70° + 20° – x + ∠PQR

= 180°

⇒ 90° + ∠PQR = 180°

⇒ ∠PQR = 180°− 90°

= 90°

Hence ,

∠PQR = 90°

Question 6.

In the given figure. p° = q° = r°, find each.

Answer

Question 7.

In the given figure, if x = 2y, find x and y

Answer

x° + y° = 180° ………….(straight angle)

But x = 2y ……..(given)

∴ 2y + y = 180°

⇒ 3y = 180°

⇒ y =180°/3

= 60°

Hence

y = 60°
and x = 2y = 2 × 60°

= 120°

Question 8.

In the adjoining figure, if b° = a° + c°, find b.

Answer

Question 9.

In the given figure, AB is perpendicular to BC at B.
Find :

(i) the value of x.
(ii) the complement of angle x.

Answer

Question 10.

Write the complement of:


Answer

(i) Complement of 25° = 90°− 25° = 65°

(ii) Complement of 90° = 90°− 90° = 0°

(iii) Complement of a° = 90°− a°

(iv)

Complement of (x + 5)° = 90°− (x + 5)°

= 90°− x − 5° = 85°− x

(v)

Complement of (30°− a)°

= 90°− (30 − a)°

= 90°− 30° + a° = 60° + a°

(vi)

Complement of 1/2 of a right angle

= 90°−1/2 right angle

= 90°-(1/2)×90°

= 90°− 45° = 45°

(vii)

Complement of 1/3 of 180°

= 90°-(1/3) of 180°

= 90°− 60° = 30°

(viii)

Complement of 21° 17′ = 90°− 21° 17′

= 68° 43′ = 68° 43′ ………….(∵ P = 60′)

Question 11.

Write the supplement of:
(i) 100°
(ii) 0°
(iii) x°
(iv) (x + 35)°
(v) (90 +a + b)° f
(vi) (110 – x – 2y)°
(vii)  of a right angle
(viii) 80° 49′ 25″
Answer

(i) Supplement of 100° = 180°− 100° = 80°

(ii) Supplement of 0° = 180°− 0° = 180°

(iii) Supplement of x° = 180°− x°

(iv)

Supplement of (x + 35)°

= 180°− (x + 35)°

= 180°− x°− 35°

= 145°− x°

(v)

Supplement of (90 + a + b)°

= 180°− (90 + a + b)°

= 180°− 90°− a°− b°

= 9°− a°− b°

= (90 − a − b)°

(vi)

Supplement of (110 − x − 2y)°

= 180°− (110 − x − 2y)°

= 180°− 110° + x°+ 2y°

= 70° + x° +  2y°

(vii)

Supplement of 1/5 of a right angle

= 180°-(1/5) of a right angle

= 180°-(1/5)×90°

= 180°− 18° = 162°

(viii)

Question 12.

Are the following pairs of angles complementary ?
(i) 10° and 80°
(ii) 37° 28′ and 52° 33′
(iii) (x+ 16)°and(74-x)°
(iv) 54° and  of a right angle.
Answer

(i)

10° and 80°

Yes, these are complementary angles as their sum = 10° + 80° = 90°

(ii)

37° 28′ and 52° 33′

No, these are not complementary angles as their sum is not 90° (37° 28′ + 52° 33′ = 90° 1′)

(iii)

(x + 16)° and (74 − x)°

Yes, these are complementary angles as their sum is 90° (x° + 16° + 74°− x° = 90°)

(iv)

54° and 2/5 of a right angle

⇒ 54° and (2/5)×90°

⇒ 54° and 36°

Yes, there are complementary angles as their sum is 90° (54° + 36° = 90°)

Question 13.

Are the following pairs of angles supplementary?

Answer

(i)

139° and 39°

No, these are not supplementary angles as their sum is not 180° (139° + 39° = 178°)

(ii)

26° 59′ and 153° 1′

Yes, there are supplementary angles as their sum is 180° (26° 59′ + 153° 1′ = 180°)

(iii)

3/10 of a right angle and 4/15 of two right angles

⇒ 3/10 of 90° and 1/15 of 180°

⇒ 27° and 48°

No, there are not supplementary angles as their sum is not 180° (27° + 48° = 75°)

(iv)

2x° + 65° and 115°− 2x°

Yes, there are supplementary angles as their sum is 180° (2x° + 65° + 115°− 2x° = 65° + 115° = 180°)

Question 14.

If 3x + 18° and 2x + 25° are supplementary, find the value of x.
Answer

if 3x + 18° and 2x + 25° are supplementary angles

so 3x + 18° + 2x + 25°

= 180°

⇒ 5x + 43° = 180°

⇒ 5x = 180°− 43°

= 137°

⇒ x =137°/5

= 27.4° or 27° 24′

Question 15.

If two complementary angles are in the ratio 1:5, find them.
Answer

Two complementary angles are in the ratio = 1 : 5

These angles be x and 5x

∴ x + 5x = 90°

⇒ 6x = 90°

⇒ x = 90°/6

= 15°

∴ Angles will be 15° and

15°× 5 = 75°

Question 16.

If two supplementary’ angles are in the ratio 2 : 7, find them.
Answer

Ratio between two supplementary angles = 2 : 7

The angles be 2x and 7x
∴ 2x + 7x = 180°

⇒ 9x = 180°

⇒ x = 180°/9

= 20°

∴ Angles are 2x = 2 × 20°

= 40°
and 7x = 7 × 20°

= 140°

Question 17.

Three angles which add up to 180° are in the ratio 2:3:7. Find them.
Answer

Ratio of three angles = 2 : 3 : 7

First angle be = 2x

second angle = 3x

and third angle = 7x

∴ 2x + 3x + 7x = 180°

⇒ 12x = 180°

⇒ x = 180°/2 = 15°

∴ First angle = 2x = 2 × 15°

= 30°

second angle = 3x = 3 × 15°

= 45°

and third angle = 7x = 7 × 15°

= 105°

Hence, the angles are 30°, 45°

and 105°

Question 18.

20% of an angle is the supplement of 60°. Find the angle.
Answer

The given angle be x

then 20% of x + 60° = 180°

⇒ 20% of x = 180°− 60° = 120°

⇒ (20/100)×x = 120°

⇒ x = (120×100)/20

⇒ x = 600°

Hence,

x = 600°

Question 19.

10% of x° is the complement of 40% of 2x°. Find x
Answer

if 10% of x° is the complement of 40% of 2x°

so 10% of x° + 40% of 2x° = 90°

⇒ (10/100)x+(40/100)×2x=90°

⇒ (10x/100)+(80x/100)=90°

⇒ (90x/100) = 90°

∴ x = (90×100)/90= 100°

Hence,

x = 100°

Question 20.

Use the adjacent figure, to find angle x and its supplement.

Answer

In the given fig.
x + 2x + 3x + 4x = 180° ……(Straight angle)

⇒ 10x = 180°

⇒ x = 180°/10

= 18°

∴ x = 18°

Its supplementary angle = 180°− 18°

= 162°

Question 21.

Find k in each of the given figures.

Answer

(i)

In the figure,

k + 150° + k − 150° + 30° + 90°

= 360° …………(Angles at a point)

⇒ 2k + 150° + 90° + 30°− 15°

= 360°

⇒ 2k + 270°− 15° = 360°

⇒ 2k = 360°− 270° + 15°

= 105°

⇒ k =105°/2

= 52.5° or 52° 30‘

so k = 52.5° or52° 30’

(ii)

In the fig.,

K + 2k + 3k + 42°

= 360° ……….(Angles at a point)

⇒ 6k + 42° = 360°

⇒ 6k = 360°− 42°

= 318°

⇒ k =318°/6

= 53°

so k = 53°

Question 22.

In the given figure, lines PQ, MN and RS intersect at O. If x : y = 1 : 2 and z = 90°, find ∠ROM and ∠POR.

Answer

In the figure, lines PQ, MN and Rs are intersecting each other at O

x : y = 1 : 2,

z = 90°

∠MOQ = ∠PON

= z …….(Vertically opposite angles)

Now, RS is a straight line

∴ x + z + y

= 180°

⇒ x + y + 90° = 180° ………(∵ z = 90°)

⇒ x + y = 180°− 90° = 90°

But x : y = 1 : 2

Let x = a then y = 2a

∴ a + 2a = 90°

⇒ 3a = 90°

⇒ a =90°/3

= 30°

∴ x = 30° and y = 2a = 2 × 30°

= 60°

Now, ∠ROM = y

= 60°

and ∠POR

= ∠SOQ ……….(Vertically opposite angles)

= x = 30°

Question 23.

In the given figure, find ∠AOB and ∠BOC.

Answer

In the figure,

5x + x + 80° + 123° + 85°

= 360° ….(Angles at a point)

⇒ 6x + 80° + 123° + 85° = 360°

⇒ 6x + 288° = 360°

⇒ 6x = 360°− 288°

= 72°

⇒ x = 72°/6 = 12°

Now, ∠AOB = 5x

= 5 × 12° = 60°
and ∠BOC = x

= 12°

Question 24.

Find each angle shown in the diagram.

Answer

From figure,

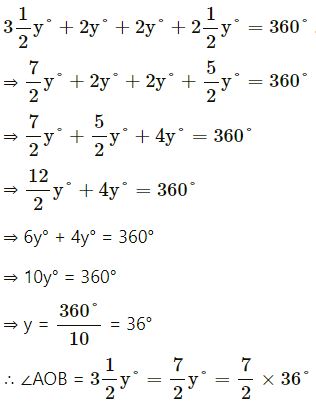
= 126°

∠BOC = 2y° = 2 × 36° = 72°

∠COD = 2y° = 72°

∠DOA =  2 (1/2)y°

=(5/2)y°
= (5/2)×36°

= 90°

Question 25.

AB, CD and EF are three lines intersecting at the same point.
(i) Find x, if y = 45° and z = 90°.
(ii) Find a, if x = 3a, y = 5x and r = 6x.

Answer

AB, CD and EF are intersecting each other at O.
and ∠DOF = x°, ∠AOC = y°
and ∠BOE = z°
But ∠DOB = ∠AOC = y° ……………(Vertically opposite angles)

Similarly, ∠COE = ∠DOF = x°
and ∠AOF = ∠BOE = z°

∴ CD is a straight line

∴ ∠COE + ∠BOE + ∠DOE = 180°

⇒ x° + z° + y° = 180°

⇒ x° + y° + z° = 180°

(i) If y = 45°, and z = 90°, then

⇒ x° + 45° + 90° = 180°

⇒ x° + 135° = 180°

∴ x° = 180°− 135° = 45°

(ii) If x = 3a, y = 5x, z = 6x,
then x + y + z = 180°

⇒ x + 5x + 6x = 180°

⇒ 12x = 180°

⇒ x = 180°/12

= 15°

But x = 3a

∴ 3a = 15°

⇒ a = 15°/3

= 5°

Hence a = 5°

---

Selina Mathematics Solutions Exe-14 B Lines and Angles for ICSE Class-7th 

In questions 1 and 2, given below, identify the given pairs of angles as

corresponding angles,

interior alternate angles,

exterior alternate angles,

adjacent angles,

vertically opposite angles

allied angles

Question 1.

(i) ∠3 and ∠6
(ii) ∠2 and ∠4
(iii) ∠3 and ∠7
(iv) ∠2 and ∠7
(v) ∠4 and∠6
(vi) ∠1 and ∠8
(vii) ∠1 and ∠5
(viii) ∠1 and ∠4
(ix) ∠5 and ∠7

Answer

(i) interior alternate angles

(ii) adjacent angles.

(iii) corresponding angles.

(iv) exterior alternate angles.

(v) allied or co-interior angles.

(vi) exterior alternate angles.

(vii) corresponding angles.

(viii) vertically opposite angles.

(ix) adjacent angles.

Question 2.

corresponding angles,

interior alternate angles,

exterior alternate angles,

adjacent angles,

vertically opposite angles

allied angles

(i) ∠1 and ∠4
(ii) ∠4 and ∠7
(iii) ∠10 and ∠12
(iv) ∠7 and ∠13
(v) ∠6 and ∠8
(vi) ∠11 and ∠8
(vii) ∠7 and ∠9
(viii) ∠4 and ∠5
(ix) ∠4 and ∠6
(x) ∠6 and ∠7
(xi) ∠2 and ∠13

Answer

(i)  vertically opposite angles.

(ii) exterior alternate angles.

(iii) vertically opposite angles.

(iv) corresponding angles.

(v) vertically opposite angles.

(vi) allied or co-interior angles

(vii)  vertically opposite angles.

(viii) adjacent angles.

(ix) allied or co-interior angles.

Question 3.

In the given figures, the arrows indicate parallel lines. State which angles are equal. Give reasons.

Answer

(i)

(ii)

from the figure,
x = y ……(vertically opposite angles)
y= l ………(alternate angles)
x = I …….(corresponding angles)
1 = n …….(vertically opposite angles)
n = r …….(corresponding angles)
∴ x = y = l = n = r
Again m = k ……(vertically opposite angles)
k = q ……..(corresponding angles)
∴ m = k = q

Question 4.

In the given figure, find the measure of the unknown angles :

Answer

a = d ….(vertically opposite angles)
d = f ……(corresponding angles)
f = 110° …….(vertically opposite angles)
∴ a = d = f = 110°
e + 110° = 180° ……(co-interior angles)
∴ e = 180°− 110° = 70°
b = c …….(vertically opposite angles)
b = e ………(corresponding angles)
e = g ……..(vertically opposite angles)
∴ b = c = e = g = 70° ”
Hence ,

a = 110°,

b = 70°,

e = 70°,

d = 110°,

e = 70°,

f= 110°

g = 70°

Question 5.

Which pair of the dotted line, segments, in the following figures, are parallel. Give reason:

Answer

(i)

From the figure,

If lines are parallel, then 120°+ 50° =180°
But there are co-interior angles
⇒ 170° = 180°. But it not true

Hence,

there are not parallel lines

(ii)

From the figure,
∠1 = 45° ……..(vertically opposite angles)
Lines are parallel if
∠1 + 135° = 180° ………(co-interior angles)
⇒ 45°+ 135° = 180°
⇒ 180° = 180° which is true.
Hence,

the lines are parallel.

(iii)

From the figure,
Lines are parallel if corresponding angles are equal
If 120° =130° which is not correct
∴ Lines are not parallel.

(iv) 

∠1 = 110° ……(vertically opposite angles)
If lines are parallel then
∠1 + 70° = 180° ……..(co-interior angles)
⇒110° + 70°

= 180°
⇒180° =180°
Which is correct.
∴ Lines are parallel.

(v) 

∠1 + 100°= 180°
⇒∠1 = 180°− 100°

= 80° ………(linear pair)
Lines l1 and l2 will be parallel If ∠1 = 70°
⇒ 80° = 70° which is not true
∴ l1 and 12 are not parallel

Again, A, l3 and l5 will be parallel
If 80° = 70° ……….(corresponding angle)
Which is not true.
∴ l3 and l5 are not parallel
But ∠1 = 80° ……..(alternate angles)
⇒ 80° = 80°
Which is true
∴ l2 and l4 are parallel

(vi) 

Lines are parallel
If alternate angles are equal
50° = 40°
Which is not true lines are not parallel.

Question 6.

In the given figures, the directed lines are parallel to each other. Find the unknown angles.



Answer

(i)

if Lines are parallel

so a = b ……(corresponding angles)

a = c

∴ a = b = c

But b = 60° ……..(vertically opposite angles)

∴ a = b = c

= 60°

(ii)

if Lines are parallel

so x = z ……(corresponding angles)

But z + y = 180° ………(linear pair)

But y = 55° ……..(vertically opposite angles)

∴ z + 55° = 180°

⇒ z = 180°− 55°

⇒ z = 125°

But x = z

∴ x = 125°

Hence,

x = 125°,

y = 55°,

z = 125°

(iii)

if Lines are parallel

∴ c = 120°

a + 120° = 180° …….(co-interior angles)

∴ a = 180°− 120° = 60°

But a = b ………(vertically opposite angles)

∴ b = 60°

hence a = 60°, b = 60°

and c = 120°

(iv)

if Lines are parallel

so x = 50° ………..(alternate angles)

and y + 120° = 180° …….(co-interior angles)

∴ y = 180°− 120° = 60°

But x + y + z = 360° ………(angles at a point)

⇒ 50° + 60° + x

= 360°

⇒ 110° + z = 360°

⇒ z = 360°− 110°

= 250°

Hence ,

x = 50°,

y = 60°,

z = 250°

(v)

if Lines are parallel

so x + 90° = 180° ………..(co-interior angles)

⇒ x = 180°− 90°

= 90°

⇒ ∠2 = x

⇒ ∠2 = 90°

But ∠1 + ∠2 + 30°

= 180° ……….(sum of angles of a triangle)

⇒ ∠1 + 90° + 30°

= 180°

⇒ ∠1 + 120° = 180°

⇒ ∠1 = 180°− 120°

= 60°

But ∠1 = k ……….(vertically oposite angle)

∴ k = 60°

But ∠1 = z ……(alternate angles)

∴ z = 60°

But k + y

= 180° ………(co-interior angles)

⇒ 60° + y = 180°

⇒ y = 180°− 60°

= 120°

Hence,

x = 90°,

y = 120°,
z = 60°,

k = 60°

(vi)

if Lines are parallel

so q = t and p = 60° ……….(corresponding angles)

But t + 60° = 180° ……..(linear pair)

⇒ t = 180°− 60° = 120°

t = r ……..(vertically opposite angles)

∴ r = 120°

q = t = 120°

x = 110° …….(vertically opposite angles)

x + s = 180° …….(linear pair)

⇒ 110° + s = 180°

⇒ s = 180°− 110° = 70°

s = ∠1 …………(corresponding angles)

∴ ∠1 = 70°

y = ∠1 = 70° ……..(vertically opposite angles)

Hence.

x = 110°,

y = 70°,

p = 60°,

q = 120°,

r = 120°,

s = 70°,

t = 120°

(vii)

if Lines are parallel

so x = p

and p + 120° = 180° ……..(alternate angles)

⇒ p = 180°− 120°

= 60°

∴ x = 60°

q = 120° ……..(corresponding angles)

y = 110° ………(vertically opposite angles)

and ∠1 + 110° = 180° …….(co-interior angles)

∴ ∠1 = 180°− 110°

= 70°

But z = ∠1 ………(vertically opposite angles)

∴ ∠z = 70°

Hence,

x = 60°,

y = 110°,

z = 70°,

p = 60°.

q = 120°

(viii)

if Lines are parallel

so y = 75° ……..(alternate angles)

∠1 + 112° = 180° ………….(linear pair)

∠1 = 180°− 112° = 68°

∠1 = x ……….(corresponding angles)

∴ x = 68°

But x + 75 + z = 180° ……(angles on a line)

⇒ 68° + 75° + z = 180°

⇒ z = 143° = 180°

⇒ z = 180°− 143° = 37°

Hence,

x = 68°,

y = 75°,

z = 37°

(ix)

if Lines are parallel

∠a = ∠1 and ∠c = ∠2 ………(alternate angles)

But ∠1 + 115°

= 180° ………(linear pair)

∴ ∠1 = 180°− 115°

= 65°

Similarly ∠2 + 120°

= 180°

∴ ∠2 = 180°− 120° = 60°

∴ ∠a = ∠1 = 65°, ∠c = ∠2 = 60°

But a + c + c = 180° …………(angles on a line)

⇒ 65° + b + 60°

= 180°

⇒ b + 125° = 180°

⇒ b = 180°− 125° = 55°

Hence,

a = 65°,

b = 55°,

c =60°

(x)

if Lines are parallel

so x + 110°

= 180° …….(co-interior angles)

x = 180°− 110°

= 70°

and x + y

= 180° ……….(co-interior angles)

⇒ 70° + y = 180°

⇒ y = 180°− 70°

= 110°

z = y ………..(corresponding angles)

∴ z = 110°

Hence,

x = 70°,

y = 110°,

z = 110°

(xi)

Draw a line parallel to the given parallel lines

∴ Lines are parallel

∴ ∠1 = 160° and ∠2

= 130° …….(alternate angles)

∴ y = ∠1 + ∠2 = 160° + 130° = 290°

But x + y = 360° ……..(angles at a point)

⇒ 290° + x

= 360°

⇒ x = 360°− 290°

= 70°

Hence,

x = 70°,

y = 290°

(xii) 

Question 7.

Find x. y and p is the given figures

Answer

(i)

From the figure,

∵ Lines are parallel

∴ x = z ………(corresponding angles)

y = 40° ……….(corresponding angles)

But x + 40° + 270°

= 360° …….(angles at a point)

⇒ x + 310°

= 360°

⇒ x = 360°− 310°

= 50°

∴ z = x = 50°

But p + z = 180° …….(linear pair)

⇒ p+ 50° = 180°

⇒ p = 180°− 50° = 130°

Hence,

x = 50°,

y = 40°,

z = 50°

p = 130°

(ii)

From the figure,

if Lines are parallel

so y = 110° ………(corresponding angles)

But 25° + p + 110° = 180° ………(angles on a line)

⇒ p + 135° = 180°

⇒ p = 180°− 135°

= 45°

⇒ x + y + 25°

= 180° ……(sum of angles of a triangle)

⇒ x + 110° + 25° = 180°

⇒ x + 135° = 180°

⇒ x = 180°− 135°

= 45°

Hence,

x = 45°,

y = 110°

p = 45°

Question 8.

Find x in the following cases :



Answer

(i)

From the figure,

∵ Lines are parallel

∴ 2x + x = 180° ………(co-interior angles)

⇒ 3x = 180°

⇒ x = 180°/3 = 60°

(ii)

From the figure,

if Lines are parallel

so 4x + 1 = 180° ………(co-interior angles)

But ∠1 = 5x ……..(vertically opposite angles)

∴ 4x + 5x = 180°

⇒ 9x = 180°

Hence,

x =180°/9

= 20°

(iii)

From the figure,

if Lines are parallel

so ∠1 + 4x = 180° ………(co-interior angles)

But ∠1 = x ……..(vertically opposite angles)

∴ x + 4x = 180°

⇒ 5x = 180°

⇒ x =180°/5

= 36°

Hence,

x = 36°

(iv)

From the figure,

∵ Lines are parallel

∴ 2x + 5° + 3x + 55° = 180° ………..(co-interior angles)

⇒ 5x + 60° = 180°

⇒ 5x = 180°− 60° = 120°

∴ x = 120°/5

= 24°

Hence,

x = 24°

(v)

From the figure,

if Lines are parallel

so ∠1 + 2x = 20° ………(alternate angles)

But ∠1 + 3x + 25° = 180° ……..(linear pair)

⇒ 2x + 20° + 3x + 25°

= 180°

⇒ 5x + 45° = 180°

⇒ 5x = 180°− 45°

= 135°

∴ x =135°/5

= 27°

(vi)

From the figure,

From 0, draw a line parallel to the given parallel lines

∴ ∠1 = 4x and ∠2 = 6x ………(corresponding angles)

But ∠1 + ∠2

= 130°

⇒ 4x + 6x

= 130°

⇒ 10x = 130°

∴ x = 130°/10

= 13°

---

Exercise – 14 C Lines and Angles ICSE Class-7th Concise Selina Mathematics

Question 1.

Using ruler and compasses, construct the following angles :
(i)30°
(ii)15°
(iii) 75°
(iv) 180°
(v) 165°
(vi) 22.5°
(vii) 37.5°
(viii) 67.5°
Answer

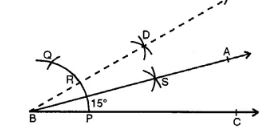
(i)

Steps :
(i) Draw a line segment BC.
(ii) With centre B and a suitable radius draw an arc meeting BC at P.
(iii) With centre P and with the same radius cut off the arc at Q.
(iv) Now with centre P and Q draw two arcs intersecting each other at R.
(v) Join BR and produce it to A, forming ∠ABC = 30°

(ii) 

Steps :
(i) Draw a line segment BC.
(ii) With centre B and a suitable radius draw an arc meeting BC at P.
(iii) With centre P and with the same radius cut off the arc at Q.
(iv) Taking P and Q as curves, draw two arcs intersecting each other at D and join BD.
(v) With centre P and R, draw two more arcs intersecting each other at S.
(vi) Join BS and produce it to A.
Then ∠ABC = 15°.

(iii) 

Steps :
(i) Draw a line segment BC.
(ii) With centre B and a suitable radius draw an arc and cut off PQ, then QR of the same radius.
(iii) With centre Q and R, draw two arcs intersecting each other at S.
(iv) Join SB.
(v) With centre Q and D draw two arcs intersecting each other at T.
(vi) Join BT and produce it to A.
Then ∠ABC = 75°.

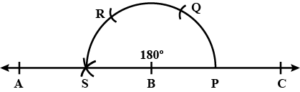
(iv)

Steps :
(i) Draw a line segment BC.
(ii) With centre B and some suitable radius draw arc meeting BC at P.
(iii) With centre P and with same radius cut of arcs PQ, QR and then RS.
(iv) Join BS and produce it to A.
Then ∠ABC = 180°.

(v)

Steps :
(i) Draw a line segment BC.
(ii) With centre B and some suitable radius draw an arc meeting BC at P.
(iii) With centre P and same radius cut off arcs PQ, QR and then RS.

(iv) Join SB.
(v) With centres R and S, draw two arcs intersecting each other at M.
(vi) With centre T and S draw two arcs intersecting each other at L.
(vii) Join BL and produce it to A. Then ∠ABC = 165°

(vi)

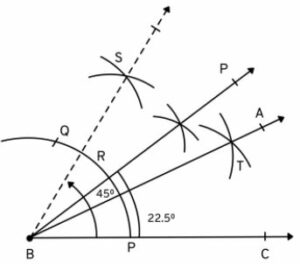
(vii) 

Steps :
(i) Draw a line segment BC.
(ii) With centre B and some suitable radius, draw an arc meeting BC at P.
(iii) With centre P and same radius cut off arcs PQ and QR.
(iv) Now bisect arc QR at S and again bisect arc QS at T.
(v) Bisect arc PT at K.
(vi) Join BK and produce it to A.
Then, ∠ABC = 3712° or 37.5.

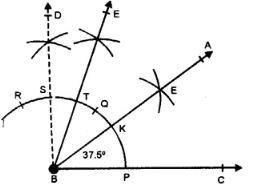
(viii) 

Steps :
(i) Draw a line segment BC.
(ii) With centre B and some suitable radius, draw an arc meeting BC at P.
(iii) With centre P and with the same radius, cut arcs PQ and then QR.
(iv) Bisect arc QR at K and again bisect arc QK at S.
(v) Bisect again arc SQ at T.
(vi) Join BT and produce it to A.
Then ∠ABC = 67 (1/2)° or 67.5°

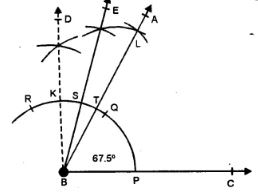
Question 2.

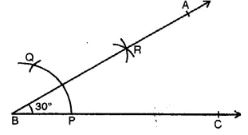
Draw ∠ABC = 120°. Bisect the angle using ruler and compasses only. Measure each 1 angle so obtained and check whether the angles obtained on bisecting ∠ABC are equal or not.
Answer

Steps :
(i) Draw a line segment BC.
(ii) With centre B and some suitable radius, draw an arc meeting BC at P.

(iii) With centre P and with the same radius, cut arcs PQ and QR.
(iv) Join BR and produce it to A.
Then ∠ABC = 120°
(v) With centres P and R, draw two arcs intersecting each other at S.
(vi) Join BS and produce it to D. BD is the bisector of ∠ABC.
On measuring each angle, it is of 60° each. Yes, both angles are equal in measure.

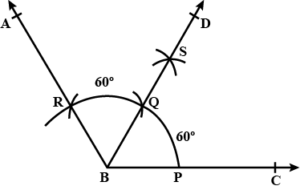
Question 3.

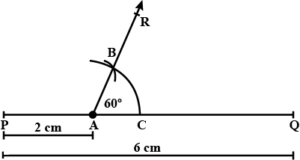
Draw a line segment PQ = 6 cm. Mark a point A in PQ so that AP = 2 cm. At point A, construct angle QAR = 60°.
Answer

Steps :
(i) Draw a line segment PQ = 6 cm.

(ii) Mark a point A on PQ so that AP = 2 cm.
(iii) With centre A and some suitable radius draw an arc meeting AQ at C.
(iv) With centre C and with the same radius, cut arc CB.
(v) Join AB and produce it to R.
Then ∠QAR = 60°

Question 4.

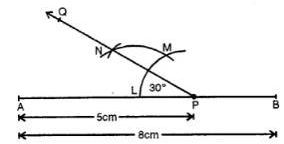
Draw a line segment AB = 8 cm. Mark a point P in AB so that AP = 5 cm. At P, construct angle APQ = 30°.
Answer

Steps :
(i) Draw a line segment AB = 8 cm.
(ii) Mark a point P in AB such that AP = 5 cm.
(iii) With centre P and some suitable radius, draw an arc meeting AB in L.
(iv) With centre L and same radius cut arc LM.
(v) Bisect arc LM at N.
(vi) Join PN and produce it to Q.
Then ∠APQ = 30°

Question 5.

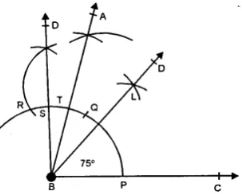
Construct an angle of 75° and then bisect it.
Answer

Steps:
(i) Draw a line segment BC.
(ii) At B, draw an angle ABC equal to 75°.

(iii) With centres P and T, draw arcs intersecting each other at L.
(iv) Join BL and produce it to D. Then BD bisects ∠ABC.

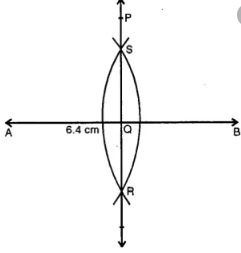
Question 6.

Draw a line segment of length 6 .4 cm. Draw its perpendicular bisector.
Answer

Steps :
(i) Draw a line segment AB = 6.4 cm.
(ii) With centres A and B and with some suitable radius, draw arcs intersecting each other at S and R.
(iii) Join SR intersecting AB at Q. Then PQR is the perpendicular bisector of line segment AB

Question 7.

Draw a line segment AB = 5.8 cm. Mark a point P in AB such that PB = 3.6 cm. At P, draw perpendicular to AB.
Answer

Steps:
(i) Draw a line segment AB = 5.8 cm.
(ii) Mark a point P in AB such that PB = 3.6 cm.
(iii) With centre P and some suitable radius draw an arc meeting AB in L.
(iv) With centre L and same radius cut arcs LM and then as N.
(v) Bisect arc MN at S.
(vi) Join PS and produce it to Q. Then PQ is perpendicular to AB at P.

Question 8.

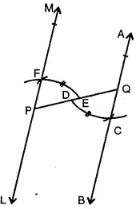
In each case, given below, draw a line through point P and parallel to AB :

Answer

 All Steps : 

(a) From P draw a line segment meeting at AB

(b) With centre Q and some suitable radius draw an arc CD.

(c) With centre P and the same radius draw another arc meeting PQ at E.

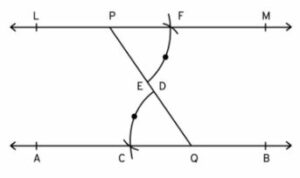
(d) With centre E and radius equal to CD, cut this arc at F

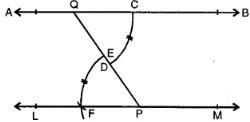
(e) Join PF and produce it to both sides to L and M. Then line LM is parallel to given line AB.

 

— End of Lines and Angles Solutions :–

 

Return to – Concise Selina Maths Solutions for ICSE Class -7 

---

Thanks