Mathematics Formula ICSE 10th Chapter-Wise

Mathematics Formula ICSE 10th Chapter-Wise. Applicable in All publications of ICSE Class-10 Mathematics. Formula of ICSE Mathematics Class 10th is very important to solve the problems.

Mathematics Formula ICSE 10th Chapter-Wise

Important formula for ICSE class 10th mathematics is given below topic wise, we advice to you also view our ICSE class -10 physics formula Chapter Wise

Goods and Service tax (GST)

 GST= output GST- input GST

Goods and Services Tax (abbreviated GST) is an indirect tax levied on the supply of goods

 Some terms related to GST 

1. Dealer. Any person who buys goods or services for resale is known as a dealer (or trader). A dealer can be a firm or a company.
2. Intra-state sales. Sales of goods and services within the same state (or Union Territory) are called intra-state sales.
3. Inter-state sales. Sales of goods and services outside the state (or Union Territory) are called inter-state sales.
4. Input GST and Output GST. GST is paid by dealers on purchase of goods and services
and is collected from customers on sale of goods and services. GST paid by a dealer is
called Input GST and GST collected from a customer is called Output GST.
5. Types of taxes under GST. There are three taxes applicable under GST:
(1) Central Goods and Services Tax (CGST).
(ii) State Goods and Services Tax (SGST) or Union Territory Goods and Services Tax
(UTGST).
Both these taxes are levied on intra-state sales ie. on sales of goods and services
within the same state. In intra-state sales, GST is divided equally among Centre and State Governments.

Banking

Shares and Dividends

( Not in Current Syllabus-2021)

Linear In equations

we know that  equality means =

Ex if A = B it is equality

but there are other conditions in which  A is Not equal B then it is called In Equations

there are four Condition of in equation

(1) a<b
(2) a>b

(3) a is less than or equal to b

(4)a is greater or equal to b

there are four law

(i) add (or subtract) the same number or expression to both sides. no sign change
(i) any number (or expression) can be transposed from one side of an in equation to the other side with the sign of the transposed number (or expression) changed (-ve
to -ve or -ve to +ve).
(iii) multiply (or divide) both sides by the same positive number.no sign change

(iv) However, when you multiply (or divide) by the same negative number, then the symbol of in equation is reversed

how solve in equation

Procedure to solve a linear in equation in one variable
(1) Simplify both sides by removing group symbols and collecting like terms.
(ii) Remove fractions (or decimals) by multiplying both sides by an appropriate fact
(L.C.M. of denominators or a power of 10 in case of decimals).
(1) Isolate all variable terms on one side and all constants on the other side. Collect h
terms when possible.
(17) Make the coefficient of the variable 1.
(v) Choose the solution set from the replacement set.

 

Quadratic Equations 

Reminder and Factor Theorem

Ratio and Proportion

Matrices

 

Arithmetic Progression

• An arithmetic progression is a sequence of numbers in which each term is derived from the preceding term by adding or subtracting a fixed number called the common difference “d”
  For example, the sequence 9, 6, 3, 0,-3, …. is an arithmetic progression with -3 as the common difference. The progression -3, 0, 3, 6, 9 is an Arithmetic Progression (AP) with 3 as the common difference.
• The general form of an Arithmetic Progression is a, a + d, a + 2d, a + 3d and so on. Thus nth term of an AP series is T_n = a + (n – 1) d, where T_n = n^th term and a = first term. Here d = common difference = T_n – T_n-1.
• Sum of first n terms of an AP: S =(n/2)[2a + (n- 1)d]
• 
• The sum of n terms is also equal to the formula where l is the last term.
• T_n = S_n – S_n-1 , where T_n = n^th term
• When three quantities are in AP, the middle one is called as the arithmetic mean of the other two. If a, b and c are three terms in AP then b = (a+c)/2

Geometric Progression

( Not in Current Syllabus-2021)

• A geometric progression is a sequence in which each term is derived by multiplying or dividing the preceding term by a fixed number called the common ratio. For example, the sequence 4, -2, 1, – 1/2,…. is a Geometric Progression (GP) for which – 1/2 is the common ratio.
• The general form of a GP is a, ar, ar², ar³ and so on.
• The nth term of a GP series is T_n = ar^n-1, where a = first term and r = common ratio = T_n/T_n-1) .
• The formula applied to calculate sum of first n terms of a GP:
• When three quantities are in GP, the middle one is called as the geometric mean of the other two. If a, b and c are three quantities in GP and b is the geometric mean of a and c i.e. b =√ac
• The sum of infinite terms of a GP series S_∞= a/(1-r) where 0< r<1.
• If a is the first term, r is the common ratio of a finite G.P. consisting of m terms, then the nth term from the end will be = ar^m-n.
• The nth term from the end of the G.P. with the last term l and common ratio r is l/(r^(n-1)) .

 

Co ordinate Geometry ,Section formula,

 Equation of Straight Line

Similarity

(must be focus on map, model word problems)

Locus

( Not in Current Syllabus-2021)

Circles

Constructions

( Not in Current Syllabus-2021)

Mensuration

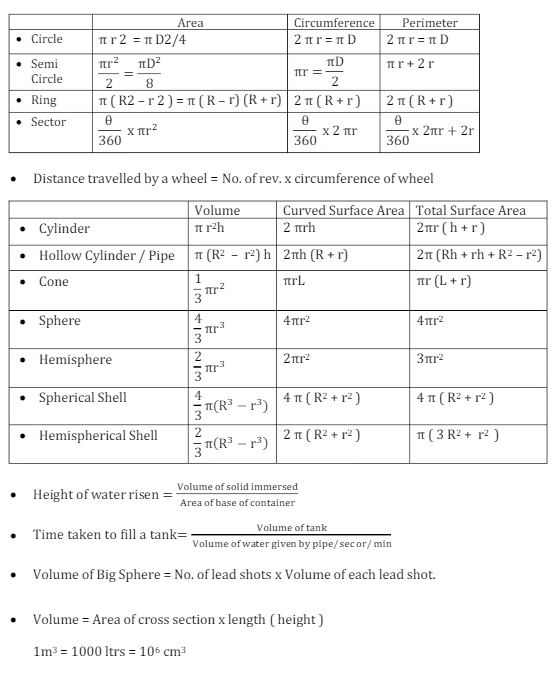
Trigonometry 

Heights and Distances

( Problems on double right angle Not in Current Syllabus-2021, only simple (single right angle) word problems

Measures of Central Tendency/ Statistics

(use any one method to find mean as 2021 further reduced syllabus )

Thanks

Return to – ICSE Class-10 Textbook Solution, Syllabus, Notes and Paper

Please Share with your ICSE friends if it is helpful