Maths Semester-1 ICSE Specimen Paper Solved Class-10 for practice. Step by step solutions of ICSE Class-10 specimen model sample paper . During solutions of semester-1 Maths specimen paper we explain with figure , graph, table whenever necessary so that student can achieve their goal in next upcoming exam of council .
Maths Semester-1 ICSE Specimen Paper Solved Class-10 for practice
| Board | ICSE |
| Class | 10th (x) |
| Subject | Maths |
| Topic | Semester-1 ICSE Specimen Paper Solved |
| Syllabus | on bifurcated syllabus (after reduction) |
| session | 2021-22 |
| Question Type | MCQ/ Objective (as prescribe by council) |
| Total question |
section-A=16 Section-B=6 Section-C=3 Total=25 |
| Max mark |
section-A=1 mark x16 Que =16 Section-B=2 mark x 6 Que=12 Section-C=4 mark x 3 Que= 12 Total =25 |
Click Below for Answer Key of Board Paper
Answer Key of Sem-1 ICSE Maths Board Paper (6th December)
ICSE Maths Specimen Paper Solution Class-10 for Semester-1 (below)
Section-A (12 mark)
Warning – please view Question Paper first before viewing solution
Question-1
If matrix A is of order 3 x 2 and matrix B is of order 2 x 2 then the matrix AB is of order
(a) 3 x 2 (b) 3 x 1 (c) 2 x 3 (d) 1 x 3
Solution
Correct option is a) 3×2
Explanation
Order of A:3×2
Order of B:2×2
Multiplication of matrices is possible if and only if the number of columns of first matrix is equal to the number of rows of second matrix
In AB
No. of columns in A is 2
No. of rows in B is 2
∴AB exists
Order of AB is ( number of rows of A x number of columns of B)
∴ Order of AB is (3×2)
Question-2
The percentage share of SGST of total GST for an Intra-State sale of an article is
(a) 25% (b) 50% (c) 75% (d) 100%
Solution
option (b) 50%
Explanation
if there is intrastate selling then total gst earn distribute equally to state SGST and central CGST
Question-3
𝐴𝐵𝐶𝐷 𝑖𝑠 𝑎 𝑡𝑟𝑎𝑝𝑒𝑧𝑖𝑢𝑚 𝑤𝑖𝑡ℎ 𝐴𝐵 𝑝𝑎𝑟𝑎𝑙𝑙𝑒𝑙 𝑡𝑜 𝐷𝐶. 𝑇ℎ𝑒𝑛 𝑡ℎ𝑒 𝑡𝑟𝑖𝑎𝑛𝑔𝑙𝑒 𝑠𝑖𝑚𝑖𝑙𝑎𝑟 𝑡𝑜 ∆𝐴𝑂𝐵
(a) ∆𝐴𝐷𝐵 (b) ∆𝐴𝐶𝐵 (c) ∆𝐶𝑂𝐷 (d) ∆𝐶𝑂D
Solutions
option (c) ∆𝐶𝑂D is correct
Explanation
in ∆ AOB and in ∆ COD
| Statement | reason |
| angle BAC= angle OCD | alternate |
| angle ABO= angle ODC | alternate |
| So ∆ AOB similar ∆ COD | by A.A. |
Question-4
The mean proportion between 9 and 16 is
(a) 25 (b) 144 (c)7 (d) 12
Solution
option (d) 12 is correct
explanation
when A,B,C are in continued proportion then B is said to be the mean proportional.
let us take A=9 and C=16 and B as X. then
A:X : : X:C
9:X : : X:16
Therefore, x = 12.
So, the mean proportional of 9 and 16 is 12.
Question-5
A man deposited ₹ 500 per month for 6 months and received ₹3300 as the
maturity value. The interest received by him is: –
(a) 1950 (b) 300 (c) 2800 (d) none of these
Solution
option (b) is correct
explanation
total money deposited in 6 month= 500 x 6= 3000
total money received = 3300
so The interest received by him is= 3300-3000=300
Question-6
The solution set representing the following number line is….
(a) {x: x ∈ R, -3 ≤ x < 2}
(b) {x: x ∈ R, -3 < x < 2}
(c) {x: x ∈ R, -3 < x ≤ 2}
(d) {x: x ∈ R, -3 ≤ x ≤2}
Solution
option (a) {x: x ∈ R, -3 ≤ x < 2} is correct
explanation
shaded dot over 3 show that 3 also include while hollow dot over 2 show that 2 is not included but less than 2
Question-7
The first three terms of an arithmetic progression (A. P.) are 1, 9, 17, then the next two terms are
(a) 25 and 35 (b) 27 and 37 (c) 25 and 33 (d) none of these
Solution
option (c) 25 and 33 correct
explanation
in AP common deference should be same
Here deference is 9-1=8
So next term obtain by just adding 8 to previous term
Question-8
If ∆𝐴𝐵𝐶 ~ ∆𝑄𝑅𝑃 𝑡ℎ𝑒𝑛 𝑡ℎ𝑒 𝑐𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑖𝑛𝑔 𝑝𝑟𝑜𝑝𝑜𝑟𝑡𝑖𝑜𝑛𝑎𝑙 𝑠𝑖𝑑𝑒𝑠 𝑎𝑟𝑒
(a) 𝐴𝐵/𝑄𝑅=𝐵𝐶/𝑅𝑃
(b) 𝐴𝐶/𝑄𝑅=𝐵𝐶/𝑅𝑃
(c) 𝐴𝐵/𝑄𝑅=𝐵𝐶/𝑄𝑃
(d) 𝐴𝐵/𝑃𝑄=𝐵𝐶/𝑅P
Solution
Option (a) 𝐴𝐵/𝑄𝑅=𝐵𝐶/𝑅𝑃 is correct
explanation
in ∆𝐴𝐵𝐶 ~ ∆𝑄𝑅𝑃
A𝐵/𝑄𝑅 (taking first 2 letter of similar ∆)
𝐵𝐶/𝑅𝑃 (taking last 2 letter of similar ∆)
Question-9
If x∈ 𝑊 , then the solution set of the inequation -x > -7, is
(a) {8,9,10…} (b) {0,1,2,3,4,5,6} (c) {0,1,2,3 …} (d) { -8, -9, -10…}
Solution
option (b) {0,1,2,3,4,5,6} is correct
explanation
-x > -7
-x by -1 < -7 by -1
sign of inequality change if multiply by negative number
x < 7
So vale of x is less than 7 which is possible in option (b) {0,1,2,3,4,5,6}
0 also included as it is Whole number
Question-10
The roots of the quadratic equation 4𝑥2- 7x + 2 = 0 are 1.390, 0. 359.The roots correct to 2 significant figures are
(a) 1.39 and 0.36
(b) 1.3 and 0.35
(c) 1.4 and 0.36
(d) 1.390 and 0.360
Solution
option (c) 1.4 and 0.36 is correct
explanation
in 1.390 taking 2 figure is 1.39 =1.4
and 0. 359 taking 2 figure is 0.36
Question-11
1.5, 3, x and 8 are in proportion, then x is equal to
(a) 6 (b) 4 (c) 4.5 (d) 16
Solution
option (b) 4 is correct
explanation
1.5/ 3,= x / 8 are in proportion
1.5 x 8 = 3 x x (cross multiplication)
on solving
x=4
Question-12
If a polynomial 2𝑥2 – 7x – 1 is divided by (x + 3), then the remainder is
(a) – 4 (b) 38 (c)-3 (d) 2
solution
option (b)38 is correct
explanation
when x+3=0
then x= -3
putting x=-3 in 2𝑥2 – 7x – 1
= 2(-3)²-7(-3)-1
= 2×9 + 21-1
=18+21-1
= 39-1
=38
Question-13
If 73 is the nth term of the arithmetic progression 3, 8, 13, 18…, then ‘n’ is
(a) 13 (b) 14 (c) 15 (d) 16
Solution
option (c) 15 is correct
explanation
here
a=3
d=8-3
=5
an = 73
an = a + (n − 1)d.
73= 3 + (n − 1) 5
73-3 = (n − 1) 5
70 = (n − 1) 5
70 / 5 = n-1
14= n-1
14+1 = n
15= n
Question-14
The roots of the quadratic equation x2+2x+1 = 0 are
(a) Real and distinct
(b) Real and equal
(c) Distinct
(d) Not real / imaginary
Solution
option (b) Real and equal is correct
explanation
if b2−4ac = 0 then root are Real and equal
Question-15
Which of the following statement is not true?
(a) All identity matrices are square matrix
(b) All null matrices are square matrix
(c) For a square matrix number of rows is equal to the number of columns
(d) A square matrix all of whose elements except those in the leading diagonal are zero is the diagonal matrix
Solution
option ((b) All null matrices are square matrix
explanation
A square matrix all of whose elements except those in the leading diagonal are zero is the diagonal identity or unit matrix
Question-16
If (x – 2) is a factor of the polynomial x3 + 2×2 – 13 x + k, then ‘k’ is equal to
(a) -10 (b)26 (c)-26 (d) 10
Solution
option (d) 10 is correct
explanation
p(x) = x^3 + 2x^2 – 13x + k
For (x – 2) to be the factor of p(x) = x^3 + 2x^2 – 13x + k
Thus (2)3 + 2(2)2 – 13(2) + k = 0
⇒ 8 + 8 – 26 + k = 0
⇒ 16-26 +k=0
⇒ -10 = – k
⇒ k = 10
Section-B (12 marks)
Maths Semester-1 ICSE Specimen Paper Solved Class-10
Question-17
A man deposited ₹1200 in a recurring deposit account for 1 year at 5% per annum simple interest. The interest earned by him on maturity is
(a) 14790 (b) 390 (c) 4680 (d) 780
Solution
option (b) 390 is correct
explanation
Deposit per month = Rs. 1200
Period = 1 years = 12 months
∴ Total principal for 1 month = (P × n(n +1))/2
= ₹ (1200 × 12 × 13)/2
= ₹ 93600
∴ Interest = PRT/100
=(93600 x 5 x 1 )/ (100 x 12)
= ₹ 390
Question-18
If x2 – 4 is a factor of polynomial x3+ x2- 4x- 4, then its factors are
(a) (x-2) (x+2) (x+1)
(b) (x-2) (x+2) (x-1)
(c) (x-2) (x-2) (x+1)
(d) (x-2) (x-2) (x-1)
Solution
option (a) (x-2) (x+2) (x+1) is correct
explanation
x3 + x2 – 4x – 4
Let x + 1 = 0
∴ x = -1
On substituting value of x in the expression
∴ f(-1) = (-1)3 + (-1)2 – 4(-1) -4 = 0
Clearly x + 1 is a factor of
f(x) = x3 + x2 – 4x – 4
∴ f(x) = (x + 1) (x2 – 4) …(By actual division)
= (x + 1) (x – 2) (x + 2)
Question-19
The following bill shows the GST rates and the marked price of articles A and B:
BILL: GENERAL STORE
Articles MP Rate
A ₹300 12%
B ₹1200 5%
The total amount to be paid for the above bill is: –
(a) 1548 (b) 1596 (c) 1560 (d) 1536
Solution
option (b) 1596 is correct
Explanation
Amount for A = 300 + 300 x 12/100
= 300+36=336
Amount for B = 1200 + 1200 x 5/100
= 1200 + 60 = 1260
total amount = Amount for A + Amount for B
= 336 + 1260
=1596
Question-20
The solution set for the linear inequation -8 ≤ x – 7 < – 4, x∈ 𝐼 is
(a) {x: x ∈ R, -1≤ x < 3}
(b) {0, 1, 2, 3}
(c) {-1, 0, 1, 2, 3}
(d) { -1, 0, 1, 2}
Solution
option (d) { -1, 0, 1, 2} is correct
Explanation
-8 ≤ x – 7 and x – 7 < -4
-8 +7 ≤ x and x < -4 +7
-1 ≤ x and x < 3
-1 ≤ x < 3
Question-21
If 5𝑎/7𝑏 =4𝑐/3𝑑 , then by Componendo and dividendo
(a) 5𝑎+7𝑏/5𝑎−7𝑏=4𝑐−3𝑑/4𝑐+ 3𝑑
(b) 5𝑎−7𝑏/5𝑎+7𝑏=4𝑐+3𝑑/4𝑐−3𝑑
(c) 5𝑎+7𝑏/5𝑎−7𝑏=4𝑐+3𝑑/4𝑐−3𝑑
(d) 5𝑎+7𝑏/5𝑎+7𝑏=4𝑐−3𝑑/4𝑐−3d
Solution
option (c) 5𝑎+7𝑏/5𝑎−7𝑏=4𝑐+3𝑑/4𝑐−3𝑑 is correct
Explanation
5𝑎/7𝑏 =4𝑐/3𝑑
5𝑎+7𝑏/5𝑎−7𝑏=4𝑐+3𝑑/4𝑐−3𝑑 applying Componendo and dividendo
Question-22
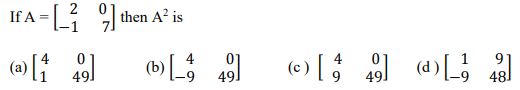
Solutions
option (b) [4 0−9 49] is correct
explanation
A² =A x A =

Section -C
Maths Semester-1 ICSE Specimen Paper Solved Class-10
Question-23
The distance between station A and B by road is 240 km and by train it is 300 km. A car starts from station A with a speed x km/hr whereas a train starts from station B with a speed 20km/hr more than the speed of the car
(i) The time taken by car to reach station B is
Solutions
option (a) 240/x is correct
explanation
Dis by road = 240
speed of car = x
Time = ?
Time = dis/ speed
= 240 / x
(ii) The time taken by train to reach station A
Solutions
option (d) 300 /𝑥+20 is correct
explanation
Dis by rail = 300
speed of train = x+20
Time = ?
Time = dis/ speed
= 300 / x+20
(iii) If the time taken by train is 1 hour less than that taken by the car, then the quadratic equation formed is
Solutions
option (b) x2 + 80x –4800=0 is correct
explanation
According condition
Time by car – Time by train = 1
(240 / x ) – (300 / x+20) =1
on simplification
x2 + 80x –4800=0
(iv) The speed of the car is
(a) 60km/hr (b) 120km/hr (c) 40km/hr (d) 80km/hr
Solutions
option (c) 40km/hr is correct
explanation
x2 + 80x –4800=0
x2 + 120x -40x –4800=0
x (x+120)-40(x+120)=0
(x+120) (x-40)= 0
applying zero product rule
either x+120 = 0
then x = -120 but speed can be negative hence ignore this value
or x-40=0
then x= 40
Question-24
In the given triangle PQR, AB || QR, QP || CB and AR intersects CB at O.
(i) The triangle similar to ΔARQ is
(a) ΔORC (b) ΔARP (c) ΔOBR (d) ΔQRP
Solutions
option (a) ΔORC is correct
explanation
ΔARQ and ΔORC
∠ARQ= ∠ORC common
∠AQR= ∠OCR alternate
So ΔARQ similar to ΔORC by AA axiom
(ii) ΔPQR ~ΔBCR by axiom
Solutions
option (b)AAA is correct
explanation
ΔPQR and ΔBCR
∠QPR= ∠CBR Alternate
∠PRQ= ∠BRC common
hence ΔPQR ~ΔBCR by AA axiom
(iii) If QC =6 cm, CR = 4 cm, BR = 3 cm. The length of RP is
(a) 4.5 cm (b) 8cm (c) 7.5cm (d) 5cm
Solutions
option (c) 7.5 cm is correct
explanation
in ΔPQR and similar ΔBCR
PQ/BC = QR/CR = PR/BR
or QR/CR = PR/BR
or 10/4 = PR/3
on simplify PR= 15/2 = 7.5
(iv) The ratio PQ: BC is
(a) 2 : 3 (b) 3 : 2 (c) 5 : 2 (d) 2 : 5
Solutions
option (c) 5 : 2 is correct
explanation
PQ/BC = QR/CR
PQ/BC = 10/4
PQ/BC = 5/2 = 5:2
Question-25
The nth term of an arithmetic progression (A.P.) is (3n + 1)
(i) The first three terms of this A. P. are
(a) 5, 6, 7 (b) 3, 6, 9 (c) 1, 4, 7 (d) 4, 7, 10
Solutions
option (d) 4, 7, 10 is correct
explanation
An= (3n + 1)
A1 = 3 x 1 +1 = 4
A2 = 3 x 2 +1= 7
A3 = 3 x 3 +1 = 10
Hence term are 4, 7, 10
(ii) The common difference of the A.P. is
(a) 3 (b)1 (c) -3 (d) 2
Solutions
option (a) 3 is correct
explanation
common difference of the A.P = term – proceeding term
= 7-4=3
(iii) Which of the following is not a term of this A.P.
(a) 25 (b) 27 (c) 28 (d) 31
Solutions
option (b) 27 is correct
explanation
term can be obtain by adding common difference to proceeding term
hence
4, 7, 10, 13,16,19,22,25,28,31
It is clear that 27 is not a term of this AP
(iv) Sum of the first 10 terms of this A.P. is
(a) 350 (b) 175 (c) -95 (d) 70
Solutions
option (b) 175 is correct
explanation
Sn = (n/2)(2a + (n – 1)d)
S10= (10/2) ((2 × 4) + ((10 – 1) × (3))
= (5) (8 + (27))
= 5 (35)
=175
— End of Semester-1 ICSE Maths Specimen Paper Solutions
Visit :- ICSE Class-10 textbook Solution , paper , Syllabus , Notes
thanks
please share with your friends



In no. 15 it is said thai all null matrix are square matrix how can this statement be true?
now focus on only sem -2 please
Very much helpful
⭐⭐⭐⭐⭐
thanks keep in touch
Are all solutions correct or can we consider these as correct answers to Maths Semester 1 Specimen paper
yes
Thank You
ok keep in touch
Thank a lot for this ….but I need more questions to practice for my boards!
how can we help you
Answer 1 and Answer 15 are wrong.
Answer 1 is (a) 3 x 2
Because in question A is 3×2 and B is 2×2.
Answer 15 is (b) All null matrices are square matrix.
This is wrong because a null matrix can be non-square also.
For e.g.
[0 0 0 0] is also null matrix but is not a square matrix.
during solutions
mistakely put the value of order b 2×1 in place of 2×2
hence ans become wrong
but now corrected
is the 1st and 15th one correct?
please now focus on sem-2
Thank you so much …..it would be even more better if u try to share in pdf form
thanks for suggestion but pdf can not be update time to time as syllabus/pattern change very soon in icse/isc due to cowid 19
thnks pandey tutoria
ok and now focus on sem-2 descriptive question of which specimen paper has been solved
Hey I just want 1help could u please provide me analysis of this paper or link of analysis. I mean I want to see how many question are from which chapter and how many marks per chapter,like in biology specimen we are given 8marks per chapter(2,3,4,5,6).
Thanks for the help BTW
we will try contact us on 8957797189