Maths Semester-2 ICSE Specimen Paper Solved Class-10

Maths Semester-2 ICSE Specimen Paper Solved Class-10 for practice.  Step by step solutions of ICSE Class-10 specimen model sample paper.  During solutions of semester-2 Maths specimen paper we explain with figure , graph, table whenever necessary so that student can achieve their goal in next upcoming exam of council .

Maths Semester-2 ICSE Specimen Paper Solved Class-10 

Board	ICSE
Class	10th (x)
Subject	Maths
Topic	Semester-2 ICSE Specimen Paper Solved
Syllabus	on bifurcated syllabus (after reduction)
session	2021-22
Question Type	Descriptive Type (as prescribe by council)
Total question	6 with all parts (Sec-A&B)
Max mark	40

Maths Semester-2 ICSE Specimen Paper Solved Class-10

Warning :- before viewing solution view Question Paper

---

Section-A

Question 1:

Choose the correct answers to the questions from the given options. (Do not copy the question, Write the correct answer only.)

(i) The point (3,0) is invariant under reflection in:

(a) The origin

(b) x-axis

(c) y-axis

(d) both x and y axes

Answer : (b) x-axis

(ii) In the given figure, AB is a diameter of the circle with centre ‘O’. If ∠𝑪OB = 55⁰ then the value of x is:

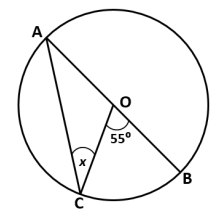
(a) 27.5⁰

(b) 55⁰

(c) 110⁰

(d) 125⁰

Answer : (a) 27.5⁰

AOC= 180-55

=125

in triangle AOC

∠A+∠O+∠C=180

but AO=OC   (radii)

x+x= 55 (ext angle = sum of opp int)

2x = 55

x= 27.5

(iii) If a rectangular sheet having dimensions 22 cm x 11 cm is rolled along its shorter side to form a cylinder. Then the curved surface area of the cylinder so formed is:

(a) 968 cm²

(b) 424 cm²

(c) 121 cm²

(d) 242 cm²

Answer : (d) 242 cm²

CSA will be same as Area of Rectangle sheet

 

(iv) If the vertices of a triangle are (1,3), (2, – 4) and (-3, 1). Then the co-ordinate of its centroid is:

(a) (0, 0)

(b) (0, 1)

(c) (1, 0)

(d) (1, 1)

Answer : (a) (0, 0)

(v) tan 𝜽 x √𝟏 − 𝒔in²𝜽 is equal to:

(a) cos 𝜽

(b) sin 𝜽

(c) tan 𝜽

(d) cot 𝜽

Answer : (b) sin 𝜽

(vi) The median class for the given distribution is:

Class Interval	1 – 5	6-10	11-15	16-20
Cumulative Frequency	2	6	11	18

(a) 1 – 5

(b) 6 – 10

(c) 11 – 15

(d) 11 – 20

Answer : (b) 6 – 10

(vii) If the lines 7𝑦 = ax + 4 and 2𝑦 = 3 − 𝑥, are parallel to each other, then the value of ‘a’ is:

(a) – 1

(b) −𝟕/𝟐

(c) −𝟐/𝟕

(d) 14

Answer : (b) −𝟕/𝟐

(viii) Volume of a cylinder is 330 cm³. The volume of the cone having same radius and height as that of the given cylinder is:

(a) 330 cm³

(b) 165 cm³

(c) 110 cm³

(d) 220 cm³

Answer : (c) 110 cm³

(ix) In the given graph, the modal class is the class with frequency:

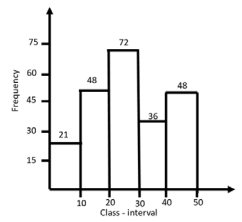
(a) 72

(b) 21

(c) 48

(d) 36

Answer : (a) 72

(x) If the probability of a player winning a game is 0.56. The probability of his losing this game is:

(a) 0.56

(b) 1

(c) 0.44

(d) 0

Answer : (c) 0.44

Click Here to View Video Solution of Sec-A

---

Maths Semester-2 ICSE Specimen Paper Solved Class-10

SECTION B

(Attempt any three questions from this Section.)

Question 2:

(i) Find the ratio in which the x-axis divides internally the line joining points A (6, -4) and B ( -3, 8).

Answer :               View Solution at bottom

(ii) Three rotten apples are accidently mixed with twelve good ones. One apple is picked at random. What is the probability that it is a good one?

Answer : 

(iii) In the given figure , AC is a tangent to circle at point B. ∆EFD is an equilateral triangle and ∠CBD = 𝟒0°. Find:

(a) ∠BFD

(b) ∠FBD

(c) ∠ABF

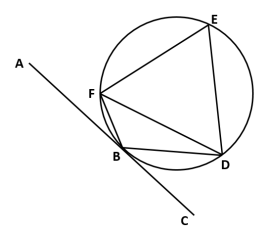
Answer : 

(iv) A drone camera is used to shoot an object P from two different positions R and S along the same vertical line QRS. The angle of depression of the object P from these two positions are 35° and 60° respectively as shown in the diagram. If the distance of the object P from point Q is 50 metres, then find the distance between R and S correct to the nearest meter.

Answer : 

Question 3:

(i) In the given figure, PT is a tangent to the circle at T, chord BA is produced to meet the tangent at P. Perpendicular BC bisects the chord TA at C. If PA = 9cm and TB = 7cm, find the lengths of:

(a) AB

(b) PT

Answer : 

(ii) How many solid right circular cylinders of radius 2 cm and height 3 cm can be made by melting a solid right circular cylinder of diameter 12 cm and height 15 cm?

Answer : 

(iii) Prove that:

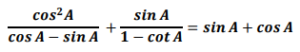
Answer : 

(iv) Use graph paper for this question, take 2 cm = 10 marks along one axis and 2 cm = 10 students along the other axis.

The following table shows the distribution of marks in a 50 marks test in Mathematics:

Marks	𝟎 − 𝟏0	1𝟎 − 20	2𝟎 − 30	3𝟎 − 40	4𝟎 − 50
No. of Students	6	10	13	7	4

 

Draw the ogive for the above distribution and hence estimate the median marks.

Answer : 

Question 4:

(i) Find the equation of the perpendicular dropped from the point P (-1,2) onto the line joining A (1,4) and B (2,3).

Answer : 

(ii) Find the mean for the following distribution:

Class Interval	2𝟎 − 40	4𝟎 − 60	6𝟎 − 80	8𝟎 − 100
Frequency	4	7	6	3

Answer : 

(iii) A solid piece of wooden cone is of radius OP = 7 cm and height OQ = 12 cm. A cylinder whose radius and height equal to half of that of the cone is drilled out from this piece of wooden cone. Find the volume of the remaining piece of wood.

(Use, 𝜋 = 𝟐𝟐/𝟕 )

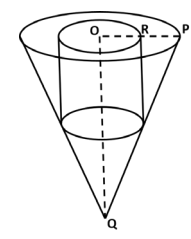
Answer : 

(iv) Use a graph sheet for this question, take 2cm = 1 unit along both x and y axis:

(a) Plot the points A (3,2) and B (5,0). Reflect point A on the y-axis to A΄. Write co-ordinates of A΄.

(b) Reflect point B on the line AA΄ to B΄. Write the co-ordinates of B΄.

(c) Name the closed figure A’B’AB.

Answer : 

Question 5:

(i) In the given figure, the sides of the quadrilateral PQRS touches the circle at A,B,C and D. If RC = 4 cm, RQ = 7 cm and PD = 5cm. Find the length of PQ:

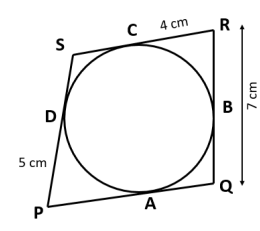
Answer : 

(ii) Prove that:

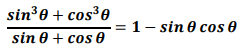
Answer : 

(iii) In the given diagram, OA = OB, ∠OAB = 𝜃 andthe line AB passes through point P (-3, 4).

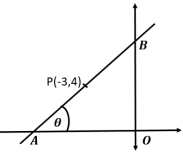
Find:

(a) Slope and inclination (𝜃) of the line AB

(b) Equation of the line AB

Answer : 

(iv) Use graph paper for this question. Estimate the mode of the given distribution by plotting a histogram. [Take 2 cm = 10 marks along one axis and 2 cm = 5 students along the other axis]

Daily wages(in ₹)	3𝟎 − 40	4𝟎 − 50	5𝟎 − 60	6𝟎 − 70	7𝟎 − 80
No. of Workers	6	12	20	15	9

Answer : 

 

Question 6:

(i) A box contains tokens numbered 5 to 16. A token is drawn at random. Find the probability that the token drawn bears a number divisible by:

(a) 5

(b) Neither by 2 nor by 3

Answer : 

(ii) Point M (2, b) is the mid-point of the line segment joining points P (a, 7) and Q (6, 5). Find the values of ‘a’ and ‘b’.

Answer : 

(iii) An aeroplane is flying horizontally along a straight line at a height of 3000 m from the ground at a speed of 160 m/s. Find the time it would take for the angle of elevation of the plane as seen from a particular point on the ground to change from 60⁰ to 45⁰.
Give your answer correct to the nearest second.

Answer : 

(iv) Given that the mean of the following frequency distribution is 30, find the missing frequency ‘f’

Class Interval	0 – 10	10 – 20	20 – 30	30 – 40	40 – 50	50 – 60
Frequency	4	6	10	f	6	4

Answer : 

---

Maths Semester-2 ICSE Specimen Paper Solved Class-10 

Video Solution of Sec-B

 

---

Return to:-    ICSE Class-10 Specimen Paper Semester-2 of 2021-22 

thanks

Please share with your ICSE friends