ML Aggarwal Equation of Straight Line MCQs Class 10 ICSE Maths Solutions Ch-12. We Provide Step by Step Answer of MCQs Questions for Ch-12 Equation of Straight Line as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Equation of Straight Line MCQs Class 10 ICSE Maths Solutions Ch-12
| Board | ICSE |
| Subject | Maths |
| Class | 10th |
| Chapter-12 | Equation of Straight Line |
| Writer / Book | Understanding |
| Topics | Solutions of MCQs |
| Academic Session | 2024-2025 |
Equation of Straight Line MCQs
Class 10 ICSE Maths ML Aggarwal Solutions Ch-12
Choose the correct answer from the given four options (1 to 13) :
Question- 1
The slope of a line parallel to y-axis is
(a) 0
(b) 1
(c) – 1
(d) not defined
Answer -1
Slope of a line parallel to y-axis is not defined. (d)
Page-247
Question -2
The slope of a line which makes an angle of 30° with the positive direction of x-axis is
(a) 1
(b) 1/√3
(c) √3
(d) -1/√3
Answer -2
Slope of a line which makes an angle of 30°
with positive direction of x-axis = tan 30°
= 1/√3 (b)
Question -3
The slope of the line passing through the points (0, – 4) and ( – 6, 2) is
(a) 0
(b) 1
(c) – 1
(d) 6
Answer -3
Slope of the line passing through the points (0, -4) and (-6, 2)
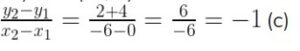
Question- 4
The slope of the line passing through the points (3, – 2) and ( – 7, – 2) is
(a) 0
(b) 1
(c) -1/10
(d) not defined
Answer- 4
Slope of the line passing through the points (3, -2) and (-7, -2)
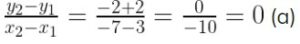
Question- 5
The slope of the fine passing through the points (3, – 2) and (3, – 4) is
(a) – 2
(b) 0
(c) 1
(d) not defined
Answer- 5
The slope of the line passing through (3, -2) and (3, -4)
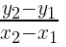
=(-4+2)/(3-3)
=-2/0
(d)
Equation of Straight Line MCQs
Class 10 ICSE Maths ML Aggarwal Solutions Ch-12
Question -6
The inclination of the line y = √3x – 5 is
(a) 30°
(b) 60°
(c) 45°
(d) 0°
Answer -6
The inclination of the line y = √3x – 5 is
√3 = tan 60° = 60° (b)
Question- 7
If the slope of the line passing through the points (2, 5) and (k, 3) is 2, then the value of k is
(a) -2
(b) -1
(c) 1
(d) 2
Answer- 7
Slope of the line passing through the points (2, 5) and (k, 3) is 2, then
m = (y2 – y1)/(x2 – x1)
⇒ 2 = (3 – 5)/(k – 2)
⇒ 2 = (-2)/(k – 2)
⇒ 2k – 4 = -2
⇒ 2k = 4 – 2
= 2
⇒ k = 2/2 = 1
Question- 8
The slope of a line parallel to the line passing through the points (0, 6) and (7, 3) is
(a) -1/5
(b) 1/5
(c) -5
(d) 5
Answer -8
Slope of the line parallel to the line passing through (0, 6) and (7, 3)
Slope of the line = 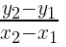
=(3-6)/(7-0)
=-3/7
(b)
Question -9
The slope of a line perpendicular to the line passing through the points (2, 5) and ( – 3, 6) is
(a) -1/5
(b) 1/5
(c) -5
(d) 5
Answer -9
Slope of the line joining the points (2, 5), (-3, 6)
= (y2 – y1)/(x2 – x1)
= (6 – 5)/(-3 – 2)
= 1/-5 = -1/5
∴ Slope of the line perpendicular to this line = 5
Question- 10
The slope of a line parallel to the line 2x + 3y – 7 = 0 is
(a) -2/3
(b) 2/3
(c) -3/2
(d) 3/2
Answer -10
The slope of a line parallel to the line 2x + 3y – 7 = 0
slope of the line
3y = – 2x + 7
⇒ y = -2/3 + 7/3
= -2/3
Class 10 ICSE Maths ML Aggarwal Solutions Ch-12
Equation of Straight Line MCQs
Question -11
The slope of a line perpendicular to the line 3x = 4y + 11 is
(a) 3/4
(b) -3/4
(c) 4/3
(d) -4/3
Answer -11
slope of a line perpendicular to the line 3x = 4y + 11 is
⇒ 4y = 3x – 11
⇒ y = 3/4 x – 11/4
Slope = 3/4
∴ Slope of the line perpendicular to this line = -4/3 (∵ m × n = -1)
Question -12
If the lines 2x + 3y = 5 and kx – 6y = 7 are parallel, then the value of k is
(a) 4
(b) – 4
(c) 1/4
(d) -1/4
Answer -12
lines 2x + 3y = 5 and kx – 6y = 7 are parallel
Slope of 2x + 3y = 5 = Slope of kx – 6y = 7
⇒ 3y – 2x + 5
⇒ y = -2/3 ×x + 5/3
Slope of 2x + 3y = 5 is -2/3
And slope of kx – 6y = 7
6y = kx – 7
⇒ y = (k/6)×x – 7/6
∴ Slope = k/6
Since both lines are parallel
∴ -2/3 = k/6
⇒ k = (-2 × 6)/3
= -4
so option (b) is correct
Question -13
If the line 3x – 4y + 7 = 0 and 2x + ky + 5 = 0 are perpendicular to each other, then the value of k is
(a) 3/2
(b) -3/2
(c) 2/3
(d) -2/3
Answer-13
(a) 3/2
Line 3x – 4y + 7 = 0 and 2x + ky + 5 = 0 are perpendicular to each other
∴ Product of their slopes = (m1×m2) = -1
Slope of 3x – 4y + 7 = 0
⇒ 4y = 3x + 7
⇒ y = 3/4 x + 7/4
Slope (m1) = 3/4
And slope of 2x + ky + 5 = 0
ky = -2x – 5
y = (-2/k) ×x – 5/k
∴ Slope (m2) = -2/k
Since the given lines are perpendicular to each other
∴ 3/4 × -2/k = -1
⇒ -6/4k = -1
⇒ -k = -6/4
⇒ k = 3/2
— : End ML Aggarwal Equation of Straight Line MCQs Class 10 ICSE Maths Ch-12 : –
Return to :- ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends


