ML Aggarwal Heights and Distances MCQs Solutions ICSE Class-10 Maths Ch-20. We Provide Step by Step Answer of MCQs Heights and Distances Questions for ICSE Class-10 APC Understanding Mathematics. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Heights and Distances MCQs Solutions ICSE Class-10 Maths Ch-20
| Board | ICSE |
| Subject | Maths |
| Class | 10th |
| Chapter-20 | Heights and Distances |
| Writer / Book | Understanding |
| Topics | Solutions of MCQs |
| Academic Session | 2024-2025 |
Heights and Distances MCQs
Choose the correct answer from the given four options (1 to 9):
Question 1. If a kite is flying at a height of 40 √3 metres from the level-ground, attached to a string inclined at 60° to the horizontal, then the length of the string is
(a) 80 m
(b) 60 √3 m
(c) 80 √3 m
(d) 120 m
Answer :
Let K is kite
Height of KT = 40 √3 m
Angle of elevation of string at the ground = 60°
Let length of string AK = x m
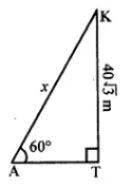
Now sin 60° = KT/AK = (40√3)/x
√3/2 = (40√3)/x
x = (40√3 × 2)/√3 = 80 m
∴ Length of string = 80 m
Question 2. If the angle of depression of an object from a 75 m high tower is 30°, then the distance of the object from the tower is
(a) 25 √3 m
(b) 50√ 3 m
(c) 75 √3 m
(d) 150 m
Answer :
Height tower AB = 75 m
C is an object on the ground and angle of depression from A is 30°.
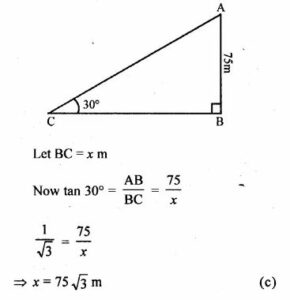
Question 3. A ladder 14 m long rests against a wall. If the foot of the ladder is 7 m from the wall, then the angle of elevation is
(a) 15°
(b) 30°
(c) 45°
(d) 60°
Answer :
Length of a ladder AB = 14 m
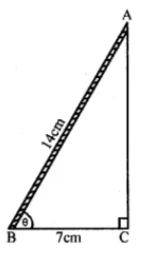
Foot of the ladder is 7 m from the wall θ is the angle of elevation
cos θ = BC/AB
= 7/14
= 1/2
= cos 60
= θ = 60°
Question 4. If a pole 6 m high casts shadow 2 √3 m long on the ground, then the sun’s elevation is
(a) 60°
(b) 45°
(c) 30°
(d) 90°
Answer :
Height of pole AB = 6 m
and its shadow BC = 2√3 m
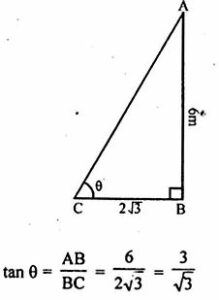
3√3/√3 x √3
= 3√3/3
= √3 = tan 60°
θ = 60°
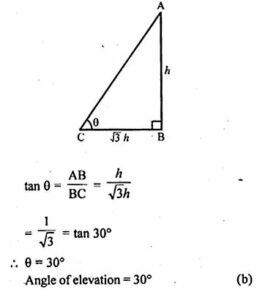
Question 5. If the length of the shadow of a tower is √3 times that of its height, then the angle of elevation of the sun is
(a) 15°
(b) 30°
(c) 45°
(d) 60°
Answer :
Let height of a tower AB = h m
Then its shadow BC = √3 hm
Question 6. In ∆ABC, ∠A = 30° and ∠B = 90°. If AC = 8 cm, then its area is
(a) 16 √3 cm²
(b) 16 m²
(c) 8 √3 cm²
(d) 6 √3 cm²
Answer :
In ∆ABC, ∠A = 30°, ∠B = 90°
AC = 8 cm
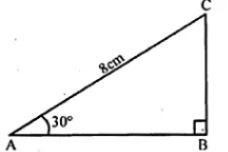
sin 30 = BC/AC
= 1/2 = BC/8
= BC = 8/2 = 4 cm
cos 30 = AB/AC
√3/2 = AB/8
= AB = 8√3/2 = 4√3 cm
near area triangle ABC = 1/2 AB x BC
= 1/2 x 4√3 x 4 cm²
= 8√3 cm²
— : End of ML Aggarwal Heights and Distances MCQs Solutions ICSE Class-10 Maths Ch-20 : –
Return to :- ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends


