ML Aggarwal Mensuration MCQs Class 10 ICSE Maths Solutions. We Provide Step by Step Answer of MCQs Questions for Mensuration as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Mensuration MCQs Class 10 ICSE Maths Solutions
| Board | ICSE |
| Subject | Maths |
| Class | 10th |
| Chapter-17 | Mensuration |
| Writer / Book | Understanding |
| Topics | Solutions of MCQs |
| Academic Session | 2024-2025 |
Mensuration MCQs
ML Aggarwal Class 10 ICSE Maths Solutions
Choose the correct answer from the given four options (1 to 32) :
Question 1. If two cylinders of the same lateral surface have their radii in the ratio 4 : 9, then the ratio of their heights is
(a) 2 : 3
(b) 3 : 2
(c) 4 : 9
(d) 9 : 4
Answer :
Ratio in two cylinder having same lateral surface area their radii is 4 : 9
Let r1 be the radius of the first and r2 be the second cylinder and h1, h2 and their heights
Let r1 = 4x and r2 = 9x
∴ 2πr1h1 = 2πr2h2
⇒ 2π× 4x × h1 = 2 × π × 9x ×h2
⇒ h1/h2 = 9x/4x
= 9 : 4
Ratio in their heights = 9 : 4 (d)
Question 2. The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3. The ratio of their volumes is
(a) 10 : 17
(b) 20 : 27
(c) 17 : 27
(d) 20 : 37
Answer :
Radii of two cylinder are in the ratio = 2 : 3
Let radius (r1) = 2x
and radius (r2) = 3x
Ratio in their height = 5 : 3
Let height of the first cylinder = 5y
and of second = 3y
Now, volume of the first cylinder
πr12h = π(2x)2 × 5h
= 20πx2y
And volume of second = π(3x)2 × 3y
= π × 27x2y
∴ Ratio is 20πx2y : 27πx2y
= 20 : 27
Mensuration MCQs
ML Aggarwal Class 10 ICSE Maths Solutions
Page 436
Question 3. The total surface area of a cone whose radius is r/2 and slant height 2l is
(a) 2πr (l + r)
(b) πr(l + r/4)
(c) πr(l + r)
(d) 2πrl
Answer :
Radius of a cone = r/2
and slant height = 2l
total surface area of a cone
πrl + πr2
= (πr/2 × 2l) + π(r/2)2
= πrl + πr2/4
= πr(l + r/4)
Question 4. If the diameter of the base of cone is 10 cm and its height is 12 cm, then its curved surface area is
(a) 60π cm2
(b) 65π cm2
(c) 90π cm2
(d) 120π cm2
Answer :
Diameter of the base of a cone = 10 cm
Radius (r) = 10/2 = 5 cm
and height (h) = 12 cm

(ML Aggarwal Mensuration MCQs Class 10)
Question 5. If the radius of a hemisphere is 5 cm, then its volume is
(a) 250/3 π cm3
(b) 500/3 π cm3
(c) 75π cm3
(d) 125/3 π cm3
Answer :
Radius of a hemisphere (r) = 5 cm
Volume = 2/3πr3
= 2/3π (5)3 cm3
= 250/3 π cm3
Question 6. If the ratio of the diameters of the two spheres is 3 : 5, then the ratio of their surface areas is
(a) 3 : 5
(b) 5 : 3
(c) 27 : 125
(d) 9 : 25
Answer :
Ratio in the diameters of two spheres = 3 : 5
Let radius of the first sphere = 3x cm
and radius of the second sphere = 5x cm
Ratio in their surface area
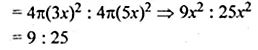
Question 7. The radius of a hemispherical balloon increases from 6 cm to 12 cm as air is being pumped into it. The ratio of the surface areas of the balloon in the two cases is
(a) 1 : 4
(b) 1 : 3
(c) 2 : 3
(d) 2 : 1
Answer :
Radius of balloon (hemispherical) in the original position = 6 cm
and in increased position = 12 cm
Ratio of their surface area = 4π(6)2 : 4π(12)2
⇒ 62 : 122
⇒ 36 : 144
⇒ 1 : 4
Question 8. If two solid hemisphere of same base radius r are joined together along with their bases, then the curved surface of this new solid is
(a) 4πr2
(b) 6πr2
(c) 3πr2
(d) 8πr2
Answer :
Radius of two solid hemispheres = r
These are joined together along with the bases
Curved surface area = 2π2 × 2 = 4πr2 (a)
(ML Aggarwal Mensuration MCQs Class 10)
Question 9. If a solid of one shape is converted to another, then the surface area of the new solid
(a) remains same
(b) increases
(c) decreases
(d) can’t say
Answer :
If a solid of one shape has conversed into another then
the surface area of the new solid will same or not same
i.e. can’t say. (d)
Question 10. The volume of the largest right circular cone that can be carved out from a cube of edge 4.2 cm is
(a) 9.7 cm3
(b) 77.6 cm3
(c) 58.2 cm3
(d) 19.4 cm3
Answer :
Edge of cube = 4.2 cm
Radius of largest cone cut out = 42.2/2 = 2.1 cm
And height = 4.2 cm
Volume = 1/3 πr2h
= 1/3 × 22/7 × 2.1 × 2.1 × 4.2 cm3
= 19.404
Therefore, 19.4 cm3
Question 11. The volume of the greatest sphere cut off from a circular cylindrical wood of base radius 1 cm and height 6 cm is
(a) 288 π cm3
(b) 4/3π cm3
(c) 6 π cm3
(d) 4 π cm3
Answer :
Radius of cylinder (r) = 1 cm
Height (h) = 6 cm
The largest sphere that can be cut off from the cylinder of radius 1 cm
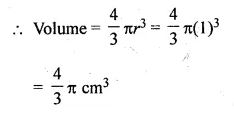
Question 12. The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is
(a) 3 : 4
(b) 4 : 3
(c) 9 : 16
(d) 16 : 9
Answer :
Ratio in volumes of two spheres = 64 : 27
Ratio of their radii = r13/r23 = 64/27
= (r1/r2)3
= (4/3)3
⇒ r1/r2 = 4/3
∴ Ratio in their surface area = 4πr12/4πr22
= r12/r22
= (4/3)2
= 16/9
∴ Ratio is 16 : 9
Question 13. If a cone, a hemisphere and a cylinder have equal bases and have same height, then the ratio of their volumes is
(a) 1 : 3 : 2
(b) 2 : 3 : 1
(c) 2 : 1 : 3
(d) 1 : 2 : 3
Answer :
If a cone, a hemisphere and a cylinder have equal bases = r (say)
and height = h in each case and r = h
Ratio in their volumes = 1/3πr2h : 2/3πr3 : πr2h
= 1/3 πr2r : 2/3 πr3 : πr2r
= 1/3 πr3 : 2/3 πr3 : πr3
= 1/3 : 2/3 : 1
= 1 : 2 : 3
Question 14. If a sphere and a cube have equal surface areas, then the ratio of the diameter of the sphere to the edge of the cube is
(a) 1 : 2
(b) 2 : 1
(c) √π : √6
(d) √6 : √π
Answer :
(d) √6 : √π
A sphere and a cube have equal surface area
Let a be the edge of a cube and r be the radius of the sphere, then
4πr2 = 6a2
⇒ π(2r)2 : 6a2 (∵ d = 2r)
⇒ d2/a2 = 6/π
⇒ d/a = √6/√π
∴ Radii d : a = √6 : √π
Question 15. A solid piece of iron in the form of a cuboid of dimensions 49 cm x 33 cm x 24 cm is molded to form a sphere. The radius of the sphere is
(a) 21 cm
(b) 23 cm
(c) 25 cm
(d) 19 cm
Answer :
Dimension of a cuboid = 49 cm × 33 cm × 24 cm
Volume of a cuboid = 49 × 33 × 24 cm3
⇒ Volume of sphere = Volume of a cuboid
Volume of a sphere = 49 × 33 × 24 cm3
∴ Radius = {Volume/(4/3.π)}1/3
= [(49 × 33 × 24 × 3 × 7)/(4 × 22)]1/3
= (49 × 7 × 3 × 3)1/3
= (7 × 7 × 7 × 3 × 3 × 3)1/3
= 7 × 3
= 21 cm
Question 16. If a solid right circular cone of height 24 cm and base radius 6 cm is melted and recast in the shape of a sphere, then the radius of the sphere is
(a) 4 cm
(b) 6 cm
(c) 8 cm
(d) 12 cm
Answer :
Height of a circular cone (h) = 24 cm
and radius (r) = 6 cm
Volume of a cone = 1/3.πr2h
= 1/3.π × 6 × 6 × 24 cm3
Volume of sphere = Volume of a cone
Now volume of sphere = 1/3π × 36 × 24 cm3
Let r be in radius of sphere
Then 4/3 πr3 = 1/3 π × 36 × 24
4r3 = 36 × 24
⇒ r3 = (36 × 24)/4
⇒ r3 = 3 × 3 × 3 × 2 × 2 × 2
⇒ r3 = 33 × 23
∴ r = 3 × 2
= 6 cm
Question 17. If a solid circular cylinder of iron whose diameter is 15 cm and height 10 cm is melted and recasted into a sphere, then the radius of the sphere is
(a) 15 cm
(b) 10 cm
(c) 7.5 cm
(d) 5 cm
Answer :
Diameter of a cylinder = 15 cm
Radius = 15/2 cm
and height = 10 cm
∴ Volume = πr2h
= π × 15/2 × 15/2 × 10 cm3
= 1125π/2 cm3
∴ Volume of sphere = 1125π/2 cm3
∴ Radius of sphere = Volume/(4/3π)1/3
= {(1125π × 3)/(2 × 4π)}1/3
= (3375/8)1/3
= {(53 × 33)/(23)}1/3
= (5 × 3)/2 cm
= 15/2
= 7.5 cm
(ML Aggarwal Mensuration MCQs Class 10)
Question 18. The number of balls of radius 1 cm that can be made from a sphere of radius 10 cm is
(a) 100
(b) 1000
(c) 10000
(d) 100000
Answer :
Radius of sphere (R) = 10 cm
Volume of sphere = 4/3πR3
= 4/3 π (10)3 cm3
= 4/3 π × 1000 cm3
And radius of one ball (r) = 1 cm
∴ Volume of one hall = 4/3 π(1)3 cm3
= 4/3.π cm3
∴ Number of balls = (4π × 1000 × 3)/(3 × 4 × π)
= 1000
Mensuration MCQs
ML Aggarwal Class 10 ICSE Maths Solutions
Page 437
Question 19. A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively is melted and recast into the form of a cone of base diameter 8 cm. The height of the cone is
(a) 12 cm
(b) 14 cm
(c) 15 cm
(d) 18 cm
Answer :
The internal diameter of the metallic shell = 4 cm
and external diameter = 8 cm
∴ Internal radius (r) = 4/2 = 2 cm
And external radius (R) = 8/2 = 4 cm
Volume of metal used = 4/3 π(R3 – r3)
= 4/3 π(43 – 23) cm3
= 4/3 × π(64 – 8) cm3
= 4/3 π × 56 cm3
Diameter of cone = 8 cm
∴ Radius of cone = 8/2 = 4 cm
⇒ Height = Volume/(1/3 πr2)
= (4π × 56 × 3)/(3 × 1 × π × 4 × 4)
= 14 cm
Question 20. A cubical ice cream brick of edge 22 cm is to be distributed among some children by filling ice cream cones of radius 2 cm and height 7 cm up to its brim. The number of children who will get the ice cream cones is
(a) 163
(b) 263
(c) 363
(d) 463
Answer :
Edge of a cubical ice cream brick = 22 cm
Volume = a3 = (22)3 = 10648 cm3
Radius (r) of ice cream cone (r) = 2 cm
and height (h) = 7 cm
Volume of one cone = 1/3πr2h
= 1/3 × 22/7 × 2 × 2 × 7 cm3
= 88/3 cm3
∴ Number of cones = (10648 × 3)/88
= 363
Question 21. Twelve solid spheres of the same size are made by melting a solid metallic cylinder of base diameter 2 cm and height 16 cm. The diameter of each sphere is
(a) 4 cm
(b) 3 cm
(b) 2 cm
(d) 6 cm
Answer :
Diameter of cylinder = 2 cm
Radius = 2/2 = 1 cm
and height = 16 cm
Volume = πr2h
= 22/7 × 1 × 1 × 16
= 352/7 cm3
∴ Volume of 12 solid spheres so formed = 352/7 cm3
∴ Volume of each sphere = 352/(7 × 12)
= 352/84 cm3
∴ Radius of each sphere = (352 × 3 × 7)/(84 × 4 × 22)1/3
= (1)1/3
= 1 cm
∴ Diameter = 2 × 1
= 2 cm
–: End of ML Aggarwal Mensuration MCQs Class 10 ICSE Maths Solutions :–
Return to :- ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends


