ML Aggarwal Section Formula MCQ Solutions ICSE Class-10 Maths Ch-11

ML Aggarwal Section Formula MCQ Solutions ICSE Class-10 Maths Ch-11. We Provide Step by Step Answer of Exercise-11 Section Formula MCQs Questions for ICSE Class-10 APC Understanding Mathematics. Visit official Website CISCE for detail information about ICSE Board Class-10.

ML Aggarwal Section Formula MCQ Solutions ICSE Class-10 Maths Ch-11

Board	ICSE
Subject	Maths
Class	10th
Chapter-11	Section Formula
Writer / Book	Understanding
Topics	Solutions of MCQ
Academic Session	2024-2025

ML Aggarwal Section Formula MCQ Solutions ICSE Class-10 Maths Ch-11

Choose the correct answer from the given four options (1 to 10) :

Question -1  The points A (9, 0), B (9, 6), C ( – 9, 6) and D ( – 9, 0) are the vertices of a

(a) rectangle
(b) square
(c) rhombus
(d) trapezium

Answer -1

A (9, 0), B (9, 6), C (-9, 6), D (-9, 0)
AB² = (x₂ – x₁)² + (y₂ – y₁)²

= (9 – 9)² + (6 – 0)²

= 0² + 6²

or   0² + 36

= 36

CD² = (-9 + 9)² + (6 – 0)²

= 0² + 6²

or  0 + 36

= 36

BC² = (9 + 9)² + (6 – 6)²

= 18² + 0²

or  324 + 0

= 324

AD² = (9 + 9)² + (0)²

= 18² + 0²

or  324 + 0

= 324

AB = CD and BC = AD so it is rectangle

Question -2 If P(a/3,  4) segment joining the points Q ( – 6, 5) and R ( – 2, 3), then the value of a is
(a) – 4
(b) – 6
(c) 12
(d) – 12

Answer -2

P(a/3,4)  is mid-point of the line segment
joining the points Q (-6, 5) and R (-2, 3)

∴ a/3 = (-6-2)/2

= -8/2 = -4

a = -4 × 3

⇒ a = -12

Question-3 If the end points of a diameter of a circle are A ( – 2, 3) and B (4, – 5), then the coordinates of its centre are
(a) (2, – 2)
(b) (1, – 1)
(c) ( – 1, 1)
(d) ( – 2, 2)

Answer -3

End points of a diameter of a circle are (-2, 3) and B (4,-5)
then co-ordinates of the centre of the circle
= {(- 2 + 4)/2, (3 – 5)/2} or (2/2, -2/2)
= (1, -1) (b)

Question -4 If one end of a diameter of a circle is (2, 3) and the centre is ( – 2, 5), then the other end is
(a) ( – 6, 7)
(b) (6, – 7)
(c) (0, 8)
(d) (0, 4)

Answer -4

One end of a diameter of a circle is (2, 3) and centre is (-2, 5)
Let (x, y) be the other end of the diameter

(2 + x)/2 = – 2

⇒ 2 + x = – 4

⇒ x = -4-2 = – 6

And (3+y)/2 = 5

⇒ 3 + y = 10

⇒ y = 10 – 3   = 7

∴ Co-ordinates of other end are (-6, 7)

Question -5  If the mid-point of the line segment joining the points P (a, b – 2) and Q ( – 2, 4) is R (2, – 3), then the values of a and b are
(a) a = 4, b = – 5
(b) a = 6, b = 8
(c) a = 6, b = – 8
(d) a = – 6, b = 8

Answer -5

the mid-point of the line segment joining the
points P (a, b – 2) and Q (-2, 4) is R (2, -3)

2 = (a – 2)/2

⇒ a – 2 = 4

⇒ a = 4 + 2 = 6

– 3 = (b – 2 + 4)/2 = (b + 2)/2

⇒ b + 2 = – 6

⇒ b = – 6 – 2 = – 8

∴ a = 6,

b = – 8

Question -6 The point which lies on the perpendicular bisector of the line segment joining the points A ( – 2, – 5) and B (2, 5) is
(a) (0, 0)
(b) (0, 2)
(c) (2, 0)
(d) ( – 2, 0)

Answer -6

the line segment joining the points A (-2, -5) and B (2, -5), has mid-point
= {(-2 + 2)/2, (-5 + 5)/2} = (0, 0)
(0, 0) lies on the perpendicular bisector of AB. (a)

Question -7 The coordinates of the point which is equidistant from the three vertices of ∆AOB (shown in the given figure) are
(a) (x, y)
(b) (y, x)
(c) (x/2, y/2)
(d) (y/2, x/2)

Answer-7

In the given figure, vertices of a ∆OAB are (0, 0), (0, 2y) and (2x, 0)
The point which is equidistant from O, A and B is the mid-point of AB.
∴ Coordinates are {(0 + 2x)/2, (2y + 0)/2} or (x, y)  (a)

Question -8 The fourth vertex D of a parallelogram ABCD whose three vertices are A ( – 2, 3), B (6, 7) and C (8, 3) is
(a) (0, 1)
(b) (0, – 1)
(c) ( – 1, 0)
(d) (1, 0)

Answer -8

ABCD is a ||gm whose vertices A (-2, 3), B (6, 7) and C (8, 3).
The fourth vertex D will be the point on which diagonals AC and BD bisect each other at O.

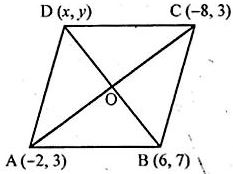
∴ Co-ordinates of O are (-2+8)/2, (3+3)/2

or (6/2, 6/2)

or (3, 3)

Let co-ordinates of D be (x, y), then

3 = (x + 6) /2    (Finding x of D)

6 = x + 6

⇒ x = 6 – 6 = 0

And 3 = (y + 7) /2  (Finding y of D)

⇒ y + 7 = 6

⇒ y = 6 – 7 = – 1

∴ Co-ordinates of D are (0, – 1)

Question -9 The points which divides the line segment joining the points (7, – 6) and (3, 4) in the ratio 1 : 2 internally lies in the
(a) Ist quadrant
(b) IInd quadrant
(c) IIIrd quadrant
(d) IVth quadrant

Answer -9

A point divides line segment joining the points
A (7, -6) and B (3, 4) in the ratio 1 : 2 internally.

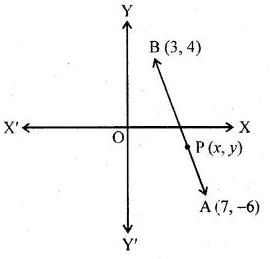
Let (x, y) divides it in the ratio 1 : 2

∴ x = (mx₂ + nx₁)/(m + n)

= (1 × 3 + 2 × 7)/(1 + 2)

or  (3 + 14)/3

= 17/3

y = (my₂ + ny₁)/(m + n)

= (1 × 4 + 2 × (-6)/(1 + 2)

or  (4 – 12)/3

= -8/3

We see that x is positive and y is negative.

∴ It lies in the fourth quadrant.

Question -10 The centroid of the triangle whose vertices are (3, – 7), ( – 8, 6) and (5, 10) is
(a) (0, 9)
(b) (0, 3)
(c) (1, 3)
(d) (3, 3)

Answer -10

Centroid of the triangle whose Vertices are (3, -7), (-8, 6) and (5, 10) is

{(3–8+5)/3, (-7+6+10)/3} or (0, 9/3)

or (0, 3) (b)

—  : End of ML Aggarwal Section Formula MCQ Solutions ICSE Class-10 Maths Ch-11 : –

Return to :- ML Aggarwal Solutions for ICSE Class-10

Thanks

Please Share with Your Friends