ML Aggarwal Trigonometric Identities MCQs Solutions ICSE Class-10 Maths Ch-18. We Provide Step by Step Answer of MCQs Trigonometric Identities Questions for ICSE Class-10 APC Understanding Mathematics. Visit official Website CISCE for detail information about ICSE Board Class-10.
ML Aggarwal Trigonometric Identities MCQs Solutions ICSE Class-10 Maths Ch-18
| Board | ICSE |
| Subject | Maths |
| Class | 10th |
| Chapter-18 | Trigonometric Identities |
| Writer / Book | Understanding |
| Topics | Solutions of MCQs |
| Academic Session | 2024-2025 |
ML Aggarwal Trigonometric Identities MCQs Solutions
ICSE Class-10 Maths Ch-18
Choose the correct answer from the given four options (1 to 12) :
Question 1. cot²θ-1/sin²θ is equal to
(a) 1
(b) -1
(c) sin2 θ
(d) sec2 θ
Answer :
(b) -1
cot2 θ – 1/sin2 θ
= cos2 θ/sin2 θ – 1/sin2 θ
= (cos2 θ – 1)/sin2 θ
= – sin2 θ/sin2 θ
= – 1
Question 2. (sec2 θ – 1) (1 – cosec2 θ) is equal to
(a) – 1
(b) 1
(c) 0
(d) 2
Answer :
(a) -1
(sec2 θ – 1)(1 – cosec2 θ)
= (1/cos2 θ – 1)(1 – 1/sin2 θ)
= (1 – cos2 θ)/cos2 θ × (sin2 θ – 1)/sin2 θ
= (- sin2 θ cos2 θ)/(sin2 θ cos2 θ) = – 1
ML Aggarwal Trigonometric Identities MCQs Solutions
ICSE Class-10 Maths Ch-11
Page-459
Question 3. tan2 θ/(1 + tan2 θ) is equal to
(a) 2 sin2 θ
(b) 2 cos2 θ
(c) sin2 θ
(d) cos2 θ
Answer :
(c) sin2 θ
tan2 θ/(1 + tan2 θ)
tan2 θ/(1 + tan2 θ) = (sin2 θ/cos2 θ)/(1 + sin2 θ/cos2 θ)
= (sin2 θ/cos2 θ)/(cos2 θ + sin2 θ)/cos2 θ
= (sin2 θ/cos2 θ) × cos2 θ/(sin2 θ + cos2 θ)
(∵ sin2 θ + cos2 θ = 1)
= sin2 θ/1
= sin2 θ
Question 4. (cos θ + sin θ)2 + (cos θ – sin θ)2 is equal to
(a) – 2
(b) 0
(c) 1
(d) 2
Answer :
(cos θ + sin θ)2 + (cos θ – sin θ)2
= cos2 θ + sin2 θ + 2 sin θ cos θ + cos2 θ + sin2 θ – 2 sin θ cos θ
so = 2(sin2 θ + cos2 θ)
Hence = 2 × 1 = 2 (d)
(∵ sin2 θ + cos2 θ = 1)
Question 5. (sec A + tan A) (1 – sin A) is equal to
(a) sec A
(b) sin A
(c) cosec A
(d) cos A
Answer :
(sec A + tan A) (1 – sin A)
= (1/cos A + sin A/cos A) (1 – sin A)
= (1 + sin A)/cos A × 1 – sin A
= {(1 + sin A)(1 – sin A)}/cos A
= (1 – sin2 A)/cos A
= cos2 A/cos A
= cos A
Question 6. (1 + tan2 A)/(1 + cot2 A) is equal to
(a) sec2 A
(b) – 1
(c) cot2 A
(d) tan2 A
Answer :
(d) tan2 A
(1 + tan2 A)/(1 + cot2 A)
(1 + tan2 A)/(1 + cot2 A) = (1 + sin2 A/cos2 A)/(1 + cos2 A/sin2 A)
= {(cos2 A + sin2 A)/cos2 A}/(sin2 A + cos2 A)/sin2 A}
= (1/cos2 A)/(1/sin2 A)
= 1/cos2 A × sin2 A/1
= sin2 A/cos2 A
= tan2 A
Question 7. If sec θ – tan θ = k, then the value of sec θ + tan θ is
(a) 1-1/k
(b) 1 – k
(c) 1 + k
(d) 1/k
Answer :
(d) 1/k
sec θ – tan θ = k
1/cos θ – sin θ/cos θ = k
(1 – sin θ)/cos θ = k
Squaring both sides, we get
(1 – sin θ)/cos θ = k
Squaring both sides, we get
{(1 – sin θ)/cos θ}2 = (k)2
⇒ (1 – sin θ)2/cos2 θ = k2
= (1 – sin θ)2/(1 – sin2 θ)
= k2
⇒ (1 – sin θ)2/(1 + sin θ)(1 – sin θ) = k2
= (1 – sin θ)/(1 + sin θ)
= k2
⇒ (1 + sin θ)/(1 – sin θ) = 1/k2
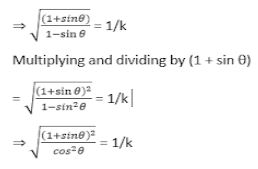
(1 + sin θ)/cos θ = 1/k
= 1/cos θ + sin θ/cos θ
= 1/k
⇒ sec θ + tan θ = 1/k
Question 8. If θ is an acute angle of a right triangle, then the value of sin θ cos (90° – θ) + cos θ sin (90° – θ) is
(a) 0
(b) 2 sin θ cos θ
(c) 1
(d) 2 sin2 θ
Answer :
sin θ cos (90° – θ) + cos θ sin (90° – θ)
= sin θ sin θ + cos θ cos θ
{ ∵ sin(90° – θ) = cosθ, cos (90° – θ) = sin θ }
= sin2 θ + cos2 θ = 1 (c)
Question 9. The value of cos 65° sin 25° + sin 65° cos 25° is
(a) 0
(b) 1
(b) 2
(d) 4
Answer :
cos 65° sin 25° + sin 65° cos 25°
so = cos (90° – 25°) sin 25° + sin (90° – 25°) cos 25°
and = sin 25° . sin 25° + cos 25° . cos 25°
therefore = sin2 25° + cos2 25°
( ∵ sin2 θ + cos2 θ = 1)
hence = 1 (b)
Question 10. The value of 3 tan2 26° – 3 cosec2 64° is
(a) 0
(b) 3
(c) – 3
(d) – 1
Answer :
3 tan2 26° – 3 cosec2 64°
= 3 tan2 26° – 3 cosec (90° – 26°)
= 3 tan2 26° – 3 sec2 26°
= 3 tan2 26° – 3 sec2 26°
= 3(tan2 26° – sec2 26°) {∵ sec2 θ – tan2 θ = 1}
= 3 × (-1)
= -3
— : End of ML Aggarwal Trigonometric Identities MCQs Solutions ICSE Class-10 Maths Ch-18 : –
Return to :- ML Aggarwal Solutions for ICSE Class-10
Thanks
Please Share with Your Friends