Mean and Median ICSE Class-6th Concise Selina Mathematics Solutions Chapter-34 . We provide step by step Solutions of Exercise / lesson-34 Mean and Median for ICSE Class-6 Concise Selina Mathematics.
Our Solutions contain all type Questions of Exe-34 A and Exe-34 B with Notes on “Mean and Median” to develop skill and confidence. Visit official Website CISCE for detail information about ICSE Board Class-6 Mathematics .
Mean and Median ICSE Class-6th Concise Selina Mathematics Solutions Chapter-34
–: Select Topics :–
What is Mean ?
The Mean and Median are the arithmetic average of a data set. This is found by adding the numbers in a data set and dividing by how many numbers there are.
Mean Formula
Mean = Sum of All observations / Number of observations
What is median
The median of a set of data is the middlemost number in the set. The median is also the number that is halfway into the set. To find the median, the data should first be arranged in order from least to greatest. A median is a number that is separated by the higher half of a data sample, a population or a probability distribution, from the lower half.
The formula to calculate the median
If the total number of observation given is odd, then the formula to calculate the median is:
Median = {(n+1)/2}thterm
If the total number of observation is even, then the median formula is:
Median = [(n/2)th term + {(n/2)+1}th]/2
To find the median, place all the numbers in value order and find the middle.
Exercise – 34 A Mean and Median for ICSE Class-6th Concise Selina Mathematics
Question- 1.
Find the mean of :
(i) 7,10, 4 and 17
(ii) 12, 9, 6,11 and 17
(iii) 3, 1, 5, 4, 4 and 7
(iv) 7, 5, 0, 3, 0, 6, 0, 9, 1 and 4
(v) 2.1, 4.5, 5.2, 7.1 and 9.3
(vi) 5, 2.4, 6.2, 8.9, 4.1 and 3.4
Answer-1:
We know that

(i)


(ii)

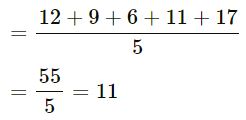
(iii)

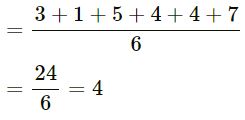
(iv)

x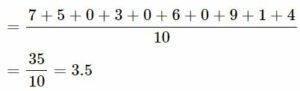
(v)

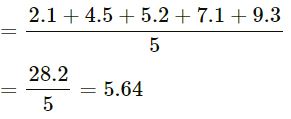
(vi)

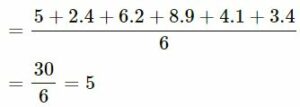
Question -2.
Find the mean of :
(i) first eight natural numbers
(ii) first six even natural numbers
(iii) first five odd natural numbers
(iv) all prime numbers up to 30
(v) all prime numbers between 20 and 40.
Answer-2:
(i) first eight natural numbers
= 1, 2, 3, 4, 5, 6, 7, 8

![]()
(ii) first six even natural numbers
= 2, 4, 6, 8, 10, 12


(iii) first five odd natural numbers
= 1, 3, 5, 7, 9

![]()
(iv) all prime numbers up to 30

![]()
(v) all prime numbers between 20 and 40.

![]()
Question- 3.
Height (in cm) of 7 boys of a locality are 144 cm, 155 cm, 168 cm, 163 cm, 167 cm, 151 cm and 158 cm. Find their mean height.
Answer-3:
Sum of the values = Sum of heights
= 144 cm + 155 cm + 168 cm + 163 cm + 167 cm + 151 cm + 158 cm = 1106 cm and
Number of values = Number of boys = 7

= 1106⁄7
=158 cm
Question -4.
Find the mean of 35, 44, 31, 57, 38, 29, 26,36, 41 and 43.
Answer-4:
Sum of the values = 35 + 44 + 31 + 57 + 38 + 29 + 26 + 36 + 41 + 43 = 380
and Number of values = 10

= 380⁄10
= 38
Question-5
The mean of 18, 28, x, 32, 14 and 36 is 23. Find the value of x.
Answer-5:
Mean = 23
Number of observation= 6
Value of x = ?

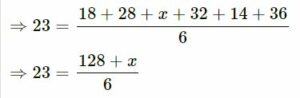
23 x 6 = 128 + x
138 = 128 + x
138-128 = x
x = 10
Question -6.
If the mean of x, x + 2, x + 4, x + 6 and x + 8 is 13, find the value of x.
Answer-6:
Mean = 13
Number of observation= 5
Value of x = ?


5x + 20 = 13 x 5
5x + 20 = 65
5x = 65 – 20
x = 45⁄5
x = 9
Selina Solutions , Mean and Median Exe-34 B for ICSE Class-6th Concise Mathematics
Question -1.
Find the median of
(i) 21, 21, 22, 23, 23, 24, 24, 24, 24, 25 and 25
(ii) 3.2, 4.8, 5.6, 5.6, 7.3, 8.9 and 91
(iii) 17, 23, 36, 12, 18, 23, 40 and 20
(iv) 26, 33, 41, 18, 30, 22, 36, 45 and 24
(v) 80, 48, 66, 61, 75, 52, 45 and 70
Answer-1
(i) Given data = 21, 21, 22, 23, 23, 24, 24, 24, 24, 25 and 25
Clearly, middle term is 24.
∴ Median = 24
(ii) Given data = 3.2, 4.8, 5.6, 5.6, 7.3, 8.9 and 9.1
Clearly, middle term is 5.6.
∴ Median = 5.6
(iii) Arranging in ascending order, we get
12, 17, 18, 20, 23, 23, 36, 40
Here, number of terms = 8 which is even
(iv)
Median = [(n/2)th term + {(n/2)+1}th]/2

(v) Arranging in ascending order, we get
45, 48, 52, 61, 66, 70, 75, 80
Here, number of terms = 8 which is even
Median = [(n/2)th term + {(n/2)+1}th]/2
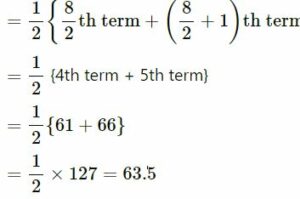
Question -2.
Find the mean and the median of :
(i) 1,3,4, 5, 9, 9 and 11
(ii) 10,12, 12, 15, 15, 17, 18, 18, 18 and 19
(iii) 2, 4, 5, 8, 10,13 and 14
(iv) 5, 8, 10, 11,13, 16, 19 and 20
(v) 1.2, 1.9, 2.2, 2.6 and 2.9
(vi) 0.5, 5.6, 3.8, 4.9, 2.7 and 4.4.
Answer-2
(i) 1,3,4, 5, 9, 9 and 11
Arranging data = 1, 3, 4, 5, 9, 9 and 11
Clearly middle term = 5
∴ Median = 5

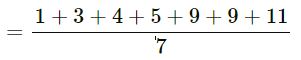
= ..42⁄7..= 6………..
mean = 6
(ii) 10,12, 12, 15, 15, 17, 18, 18, 18 and 19
Arranging data: 10,12, 12, 15, 15, 17, 18, 18, 18 and 19
Here, number of terms = 10 which is even
Median = [(n/2)th term + {(n/2)+1}th]/2

= 1⁄2. x 32
= 16
now mean

![]()
= 154⁄10. = 15.4
(iii) 2, 4, 5, 8, 10,13 and 14
Arranging data = 2, 4, 5, 8, 10, 13 and 14
Clearly, middle term is 8
∴ Median = 8

![]()
= 56⁄7. = 8
(iv) 5, 8, 10, 11,13, 16, 19 and 20
Arranging data: 5, 8, 10, 11,13, 16, 19 and 20
Here, number of data = 8 which is even
Median = [(n/2)th term + {(n/2)+1}th]/2

= 1⁄2. x 24
=1 2

![]()
= 102⁄8. = 17.75
(v) 1.2, 1.9, 2.2, 2.6 and 2.9
Given data = 1.2, 1.9, 2.2, 2.6 and 2.9
Clearly, middle term is 2.2
∴ Median = 2.2


(vi) 0.5, 5.6, 3.8, 4.9, 2.7 and 4.4.
Arranging in ascending order, we get
0.5, 2.7, 3.8, 4.4, 4.9, 5.6
Here, number of terms(n) = 6 which is even
Median = [(n/2)th term + {(n/2)+1}th]/2



= 21.9⁄6 = 3.65
–: End of Mean and Median ICSE Class-6th Solutions :–
Return to – Concise Selina Maths Solutions for ICSE Class -6
Thanks


