ML Aggarwal Measures of Central Tendency Exe-21.1 Class 10 ICSE Maths Solutions

ML Aggarwal Measures of Central Tendency Exe-21.1 Class 10 ICSE Maths Solutions. We Provide Step by Step Answer of  Exe-21.1 Questions for Measures of Central Tendency as council prescribe guideline for upcoming board exam. Visit official Website CISCE for detail information about ICSE Board Class-10.

ML Aggarwal Measures of Central Tendency Exe-21.1 Class 10 ICSE Maths Solutions

Board	ICSE
Subject	Maths
Class	10th
Chapter-21	Measures of Central Tendency
Writer / Book	Understanding
Topics	Solutions of Exe-21.1
Academic Session	2024-2025

Measures of Central Tendency Exe-21.1

ML Aggarwal Class 10 ICSE Maths Solutions

Page 493

Question 1. Calculate the arithmetic mean of 5.7, 6.6, 7.2, 9.3, 6.2.

Answer :

Sum of 5 observations = 5.7 + 6.6 + 7.2 + 9.3 + 6.2 = 35.0
∴ Mean = 35/5 = 7

Question 2. The marks obtained by 15 students in a class test are 12, 14, 07, 09, 23, 11, 08, 13, 11, 19, 16, 24, 17, 03, 20 find

(i) the mean of their marks.
(ii) the mean of their marks when the marks of each student are increased by 4.
(iii) the mean of their marks when 2 marks are deducted from the marks of each student.
(iv) the mean of their marks when the marks of each student are doubled.

Answer :

Sum of marks of 15 students.
= 12 + 14 + 07 + 09 + 23 + 11 + 08 + 13 + 11 + 19 + 16 + 24 + 17 + 03 + 20
= 207

(i) Mean = 207/15

= 13.8

(ii) If mark of each student is increased by 4, total increased marks = 4×15 = 60

Total increase in sum of marks = 207+60 = 267

mean = sum of marks/number of students

mean = 267/15 = 17.8

Hence the mean is 17.8.

(iii) If mark of each student is deducted by 2, total deducted marks = 2×15 = 30

Total decrease in sum of marks = 207-30 = 177

mean = sum of marks/number of students

mean = 177/15 = 11.8

Hence the mean is 11.8.

(iv) If mark of each student is doubled, then new sum of marks = 2 × 207 = 414

mean = new sum of marks/number of students

mean = 414/15 = 27.6

Hence the mean is 27.6.

Question 3.

(a) The mean of the numbers 6, y, 7, x, 14 is 8. Express y in terms of x.
(b) The mean of 9 variates is 11. If eight of them are 7, 12, 9, 14, 21, 3, 8 and 15 find the 9th variate.

Answer :

(a) Sum of numbers = 6 + y + 7 + x + 14

= 27 + x + y …(i)
But mean of 5 numbers = 8
∴ Sum = 8 × 5 = 40 …(ii)
From (i) and (ii)
27 + x + y = 40
⇒ x + y = 40 – 27 = 13
∴ y = 13 – x

(b) Mean of 9 variates = 11

∴ Total sum =11 × 9 = 99
But sum of 8 of these variates
= 7 + 12 + 9 + 14 + 21 + 3 + 8 + 15 = 89
∴ 9th variate = 99 – 89 = 10

Question 4.

(a) The mean age of 33 students of a class is 13 years. If one girl leaves the class, the mean becomes 12(15/16) years. What is the age of the girl ?
(b) In a class test, the mean of marks scored by a class of 40 students was calculated as 18.2. Later on, it was detected that marks of one student was wrongly copied as 21 instead of 29. Find the correct mean.

Answer :

(a) Mean age of 33 students = 13 years

Total age = 13 × 33 = 429 years

After a girl leaves, the mean of 32 students becomes
12.15/16 = 207/16

Now sum of ages = 32 × 207/16

= 414

So the age of the girl who left = 429-414 = 15 years.

Hence the age of the girl who left is 15 years.

(b) Mean of marks = 18.2

Number of students = 40

Total marks of 40 students = 40 × 18.2 = 728

Difference of marks when copied wrongly = 29 – 21 = 8

So total marks = 728 + 8 = 736

mean = 736/40

= 18.4

Hence,

the correct mean is 18.4.

Question 5. Find the mean of 25 given numbers when the mean of 10 of them is 13 and the mean of the remaining numbers is 18.

Answer :

Mean of 10 numbers = 13
Sum = 13 × 10 = 130
and mean of remaining 15 numbers = 18
Sum = 18 × 15 = 270
Total sum of 25 numbers = 130 + 270 = 400
Mean of 25 numbers = 400/25 = 16

Question 6. Find the mean of the following distribution:

Answer :

Question 7. The contents of 100 match boxes were checked to determine the number of matches they contained

(i) Calculate, correct to one decimal place, the mean number of matches per box.
(ii) Determine how many extra matches would have to be added to the total contents of the 100 boxes to; bring the mean upto exactly 39 matches. (1997)

Answer :

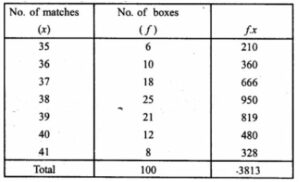
= 38.13

= 38.1

Hence the mean is 38.1.

(ii) New mean = 39

Ʃfx = 39 × 100 = 3900

So number of extra matches to be added = 3900 – 3813 = 87

Hence the number of extra matches to be added is 87.

---

Measures of Central Tendency Exe-21.1

ML Aggarwal Class 10 ICSE Maths Solutions

Page 494

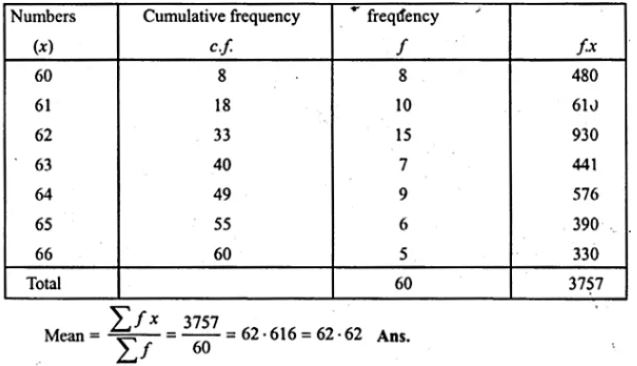
Question 8. Find the mean for the following distribution by short cut method

Answer :

Question 9.

(i) Calculate the mean wage correct to the nearest rupee (1995)
(ii) If the number of workers in each category is doubled, what would be the new mean wage ?

Answer :

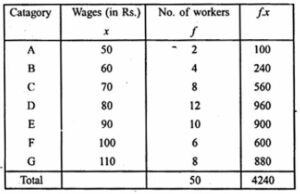
(i) Mean = Ʃfx/Ʃf

= 84.8

= 85

Hence the mean is 85.

(ii) If number of workers is doubled, then total number of workers = 50×2 = 100

So wages will be doubled.

Total wages = 4240 × 2 = 8480

Mean = Ʃfx/Ʃf

= 8480/100

= 84.8

= 85

Hence the mean is 85.

Question 10. If the mean of the following distribution is 7.5, find the missing frequency ” f “.

Answer :

Question 11. Marks obtained by 40 students in a short assessment are given below, where a and b are two missing data.

If the mean of the distribution is 7.2, find a and b.

Answer :

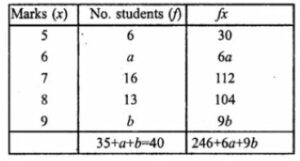
Given number of students = 40

Ʃf = 35 + a + b = 40

⇒ a + b = 40 – 35 = 5

⇒ a = 5 – b …(i)

Mean = Ʃfx/Ʃf

Given mean = 7.2

(246 + 6a + 9b) /40 = 7.2

⇒ (246 + 6a + 9b) = 40 × 7.2

⇒ (246 + 6a + 9b) = 288

⇒ 6a + 9b = 288 – 246

⇒ 6a + 9b = 288 – 246

⇒ 6a + 9b = 42

⇒ 2a + 3b = 14 …(ii)

Substitute (i) in (ii)

2(5 – b) + 3b = 14

⇒ 10 – 2b + 3b = 14

⇒ 10 + b = 14

⇒ b = 14 – 10 = 4

⇒ a = 5 – 4 = 1

Hence,

the value of a and b is 1 and 4 respectively.

Question 12. Calculate the mean of the following distribution:

Answer :

Consider the following distribution :

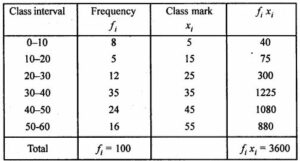
Mean = Ʃf_ix_i/Ʃf_i

= 3600/100

= 36

Hence, the mean of the distribution is 36.

Question 13. Calculate the mean of the following distribution using step deviation method:

Answer :

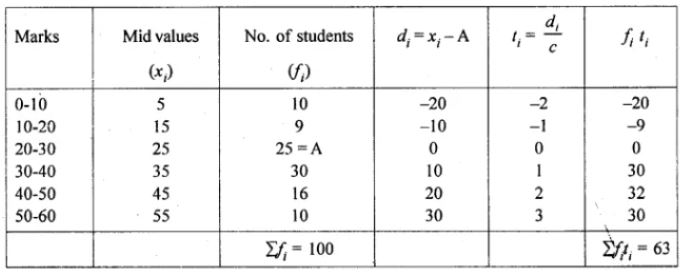
By step deviation method, Mean = x̄ = A+h∑f_iu_i /∑f_i

= 25 + 10(63/100)

= 25 + 10 × 0.63

= 25 + 6.3

= 31.3

Hence, the mean of the distribution is 31.3.

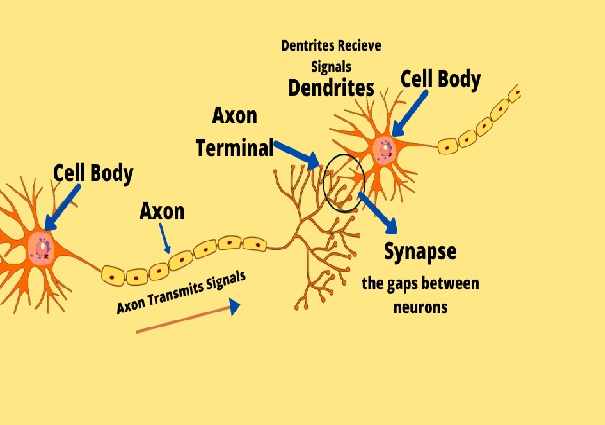
Question 14. The data on the number of patients attending a hospital in a month are given below. [3]
Find the average (mean) number of patients attending the hospital in a month by using the shortcut method.
Take the assumed mean as 45. Give your answer correct to 2 decimal places.

Answer :

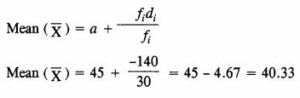
Question 15. The following table gives the daily wages of workers in a factory:

Calculate their mean by short cut method.

Answer :

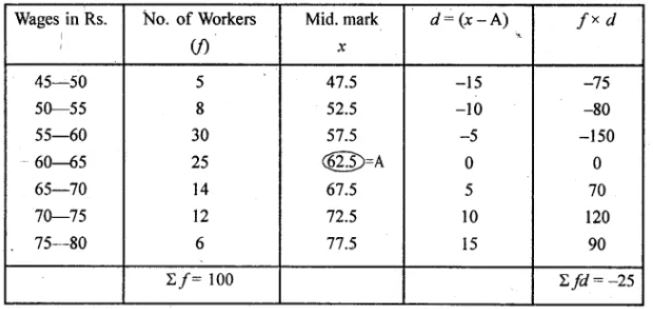
By short cut method, Mean = x̄ = A +∑f_id_i /∑f_i

= 62.5 + -25/100

= 62.5 – 0.25

= 62.25

Hence the mean of the distribution is Rs.62.25.

Question 16. Calculate the mean of the distribution given below using the short cut method.

Answer :

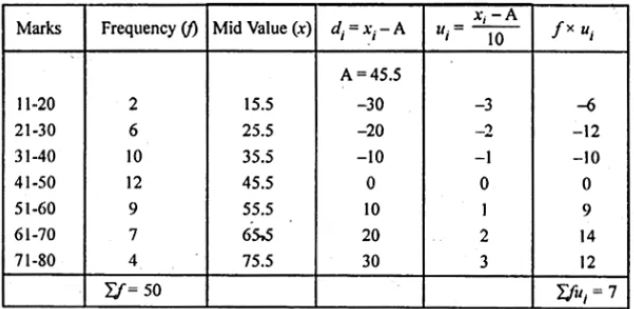
By short cut method, Mean = x̄ = A + ∑f_id_i/∑f_i

= 45.5 + 70/50

= 45.5 + 1.4

= 46.9

Hence, the mean of the distribution is Rs.46.9.

---

Measures of Central Tendency Exe-21.1

ML Aggarwal Class 10 ICSE Maths Solutions

Page 495

Question 17. A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days a students was absent.

Answer :

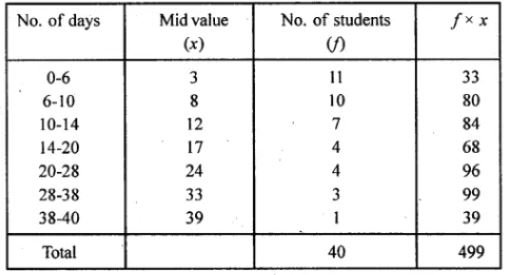
Mean = Ʃf_ix_i/Ʃf_i

= 499/40

= 12.475

Question 18. If the mean of the following distribution is 24, find the value of ‘a’.

  

Answer :

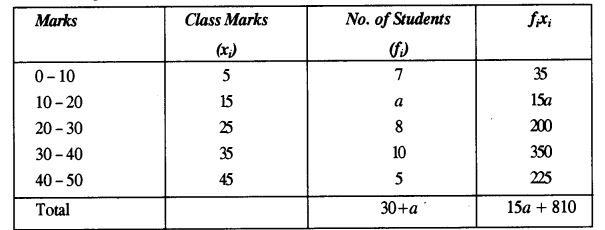
Mean = 24 (given)
∴ (15a + 810)/(30 + a) = 24
15a + 810 = 720 + 24a
⇒ 24a – 15a = 810 – 720
⇒ 9a = 90
⇒ a = 10
Hence, the value of a is 10.

Question 19. The mean of the following frequency distribution is 57.6 and the sum of all the frequencies is 50. Find the values of p and q.

Answer :

Mean = 57.6
and sum of all frequencies = 50

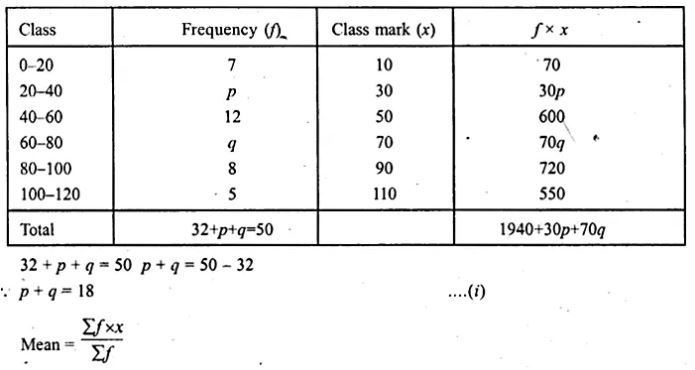
57.6 = (1940 + 30P + 70q)/50

⇒ 57.6 × 50 = 1940 + 30P + 70q

⇒ 2880 = 1940 + 30P + 70q

⇒ 2880 – 1940 = 30P + 70q

⇒ 940 = 30P + 70q

⇒ 94 = 3P + 7q …(ii)

Substitute (i) in (ii)

94 = 3(18 – q) + 7q

⇒ 94 = 54 – 3q + 7q

⇒ 94 – 54 = 4q

⇒ 40 = 4q

⇒ q = 40/4 = 10

⇒ P = 18 – 10 = 8

Hence, the value of P and q is 8 and 10 respectively.

Question 20. The following table gives the life time in days of 100 electricity tubes of a certain make :

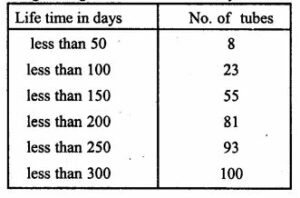
Find the mean life time of electricity tubes.

Answer :

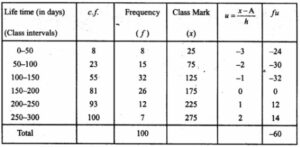
Class mark (x_i) = (upper limit + lower limit)/2

Let assumed mean (A) = 175

Class size (h) = 50

= 175 + 50 × -0.60

= 175 + 50(-60/100)

= 175 – 30

= 145

Question 21. Using the information given in the adjoining histogram, calculate the mean correct to one decimal place.

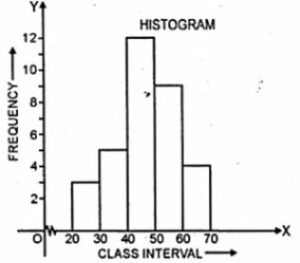
Answer :

From the histogram given, we represent the information in the following table :

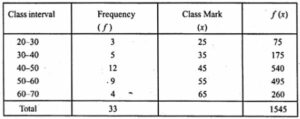
By short cut method, Mean = x̄ = A+∑f_id_i /∑f_i

_{= 45 + 60/33}

= 45 + 1.81

= 46.81

= 46.8

-: End of ML Aggarwal Measures of Central Tendency Exe-21.1 Class 10 ICSE Maths Solutions :–

Return to :- ML Aggarwal Solutions for ICSE Class-10

Thanks

Please Share with Your Friends